Journal of Global Positioning Systems (2008)
Vol. 7, No. 1 : 1-8
GPS RTK Performance Characteristics and Analysis
Yanming Feng
Faculty of Information Technology, Queensland University of Technology, Australia
Jinling Wa ng
School of Surveyin g and Spatial Information Systems, The University of New Sou th Wales, Australia
Abstract
Global Navigation Satellite Systems (GNSS) provide
various types of positioning state solutions, such as
single point positioning (SPP), precise point positioning
(PPP), differential GPS (DGPS) and real time kinematic
(RTK) solutions. These solutions are obtained involving
different data types, receivers, samples, serving different
classes of users. Previous studies on performance
characteristics have mainly focused on SPP solutions for
safety-of-life navigation applications. This paper defines
various useful performance characteristics for carrier
phase Ambiguity Resolution (AR) and Position
Estimation (PE) solutions in the RTK context. These
parameters, including base-rover distance, time-to-first
fix (TTFF), AR reliability, RTK accuracy, availability
and integrity, etc, effectively represent the performance
of a commercial RTK system and can be used to
evaluate RTK systems and algorithms, and processing
strategies through extensive experimental results.
Statistical results from extensive field experiments were
obtained using a commercial RTK system,
demonstrating convincing overall system performance in
different perspectives. Experimental results from three
baselines were also analysed using a version of research-
oriented RTK software, showing that AR performance
improvement of using Wide-lane (WL) and Narrow-lane
(NL) signals with respect to the original L1 and L2
signals when the baselines exceed 20 kilometres.
Key words: GNSS, real time kinematic (RTK)
positioning, performance characteristics, ambiguity
resolution (AR), RTK integrity.
1. Introduction
Global Navigation Satellite Systems (GNSS) positioning
may be classified into several different types, depending
on (i) the types of measurements used in the positioning
estimation, (ii) the data epochs or data arcs required to
create a set of solutions, and (iii) the number of receivers
involved in the positioning operations. Single Point
Positioning (SPP) produces navigation solutions with
pseudorange measurements from a single receiver and a
single epoch. Precise Point Positioning (PPP) solutions
are obtained using both code and phase measurements
from a single receiver, but a period of observations, e.g.,
tens of minutes to hours, regardless of kinematic or static
user applications. Differential GPS (DGPS) solutions are
based on code measurements from a single epoch as
well, but using the differential corrections from a
reference station or network. Real Time Kinematic
(RTK) positioning makes use of carrier phase
measurements in the differential positioning mode,
ideally, from a single epoch. Practically, multiple epochs
or a short period of observations are often involved to
achieve reliable AR, while the RTK solutions are derived
from the current epochs.
Different characteristics are required to evaluate various
GNSS solutions, to address positioning performance
requirements for various applications. Code based SPP
and DGPS navigation are the simplest and most robust
positioning modes, but, evaluation of code based
navigation solutions has been a quite involved problem.
The parameters of accuracy, availability, continuity and
integrity are defined to evaluate the performance of
navigation solutions in aviation navigation (Langley,
1999). For instance, availability is an instantaneous
performance characteristic defined as a percentage of
time during which the service is available at a certain
accuracy. Integrity relates to the level of trust that can be
placed in the information provided by the navigation
system. It includes the ability of the navigation system to
provide timely and valid warnings to users when the
system must not be used for the intended operation or
phase of flight. GPS does not provide integrity
information to users.
In the context of integrity, three parameters, integrity
risk, time to alert and alarm-limit are defined.
Furthermore, various methods for monitoring the

Feng et al: GPS RTK Performance Characteristics and Analysis 2
integrity of GPS SPP solutions have been proposed (i)
external monitoring, which relies on a number of ground
stations, where a faulty individual satellite is identified
and a warning is sent to users within the time-to-alert
required. The typical example is the Wide Area
Augmentation Systems (WAAS) (Enge et al, 1996;
Walter, 2002), (ii) Receiver Autonomous Integrity
Monitoring (RAIM) (Brown, 1996), which is applicable
within a user receiver to autonomously determine system
integrity. The method attempts to detect the existence of
faulty measurements and identification of unhealthy
satellites.
RTK positioning is a much more complicated and
vulnerable process, aiming to achieve the accuracy as
high as centimetres with as few as possible data epochs
in real time for any user kinematics. Therefore a greater
care has to be taken of to characterise the performance
and to address the concerns of liability-critical
professional positioning users, such as surveying, data
acquisitions, machine automation in precision
agriculture, mining and construction and future safety-
related vehicle navigation. In many applications, users
are concerned about not only accuracy, but also
availability and integrity of the solutions. For instance, in
an open cut mine, the cost of every hour of RTK service
outages to the productions would reach the level of one
million (Higgins, 2007).
However, RTK performance characteristics are much
less studied and understood than those of the SPP
solutions. This paper presents a systematic review for
RTK performance characteristics and then evaluates the
GNSS ambiguity resolution (AR) and RTK performance
with GPS measurements in terms of the various RTK
performance parameters, which may not necessarily be
suitable for real time quality control purposes. In the
following sections, we first present the definitions of
various performance parameters for AR and RTK
solutions in order to comprehensively evaluate
performance of a RTK system. Next, we outline the
linear equations for AR and Position Estimation (PE)
with the specific WL and NL signals, to conceptually
demonstrate the dependence of performance on the
models and algorithms. In the forth section, we will first
examine the statistical results for the different
performance parameters of a commercial RTK system,
HD-RTK2TM, according to its extensive data sets of
different baselines. Utilising the research version of the
QUT-RTK software, we then compare AR performance
improvement of the WL and NL signals with respect to
the use of the original L1 and L2 signals. In this analysis,
three 24-h RINEX data sets over the baselines of 21, 56
and 74 km will be analysed. Finally, the major results of
RTK performance characterisations and extensive
numerical analyses are outlined.
2. Performance Characteristics of a RTK
System
A RTK system consists of a continuous operating
reference station network and data links between a
network server and reference stations and between the
server and user-terminals. The reference network
comprises a minimum of one reference station and a
network server with a data processing facility. Data links
set up between the network server and user receivers
provide or deliver the differential corrections to user-
terminals. The user terminal is generally equipped with a
GNSS RTK receiver and a communication device and a
user control/interface unit where RTK solutions are
integrated or interfaced with a particular application. To
completely assess the performance of a RTK system, the
following parameters should be considered (Feng &
Wang, 2007):
Base-rover distance, which is the maximum radius of
circle coverage, where a signal base station can serve
effectively, allowing the users to receive the RTCM
messages within certain latency and obtain its RTK
solutions epoch-by-epoch. A relevant concept is the
inter-station distance in the network-based RTK case. As
shown in Fig. 1, the base-rover distance D is
approximately equivalent to 0.5774 times of the inter-
station distance S. For instance in the Virtual Reference
Station (VRS) system where the maximum inter-station
spacing is S=70 km, the equivalent maximum base-rover
distance is about 40 km. The distance limitation is
mainly caused by the strong dependence of the
ionospheric biases on the separation of two receivers.
The next distance-dependent error factor is the residual
tropospheric errors after modelling corrections. The
effect of broadcast orbital errors is relatively small and
may be ignored. The system performance is considered
more desirable if a longer base-rover distance is allowed.
Timeliness of RTCM message, which is defined as the
time latency of the latest RTCM message available for
users with respect to the user time instant at which the
user states are needed to compute. Users will need to
predict the ranging corrections to the most current time
instant when the user-terminal produce RTK solutions.
This latency is the sum of delays caused by data
processing at the base station/network centre and data
transmissions from base stations to network centre, and
messages from the network server to users, typically one
to a few seconds. This parameter is obtainable from
statistical results for a given operational environment
and communication links.
Another related parameter is the communication rates,
for instance, 1Hz, or 5Hz and 10Hz. The higher
communication rates are required for higher position
update rates and control of position accuracy.

Feng et al: GPS RTK Performance Characteristics and Analysis 3
Fig. 1 Relation of Inter-station distance S and equivalent
base-rover distance D=0.5774S
The above two parameters are used to evaluate the
performance at the system level. At the user terminal,
performance of a RTK system may be evaluated using
the following characteristics, which may vary with the
system performance parameters.
Time To First-Fix (TTFF). This is referred to the time
period required to resolve or fix sufficient integer
ambiguities of the linear equation system, then perform
position estimation.. In some literature, this parameter is
known as “Time To Ambiguity-Fix (TTAF)” or
“initialisation time” of the RTK system. However, TTAF
is more suitable for more general situations where all the
integer parameters are resolved and fixed independently
at each epoch, involving measurements from single or
multiple most recent epochs. It is most desirable if the
RTK system always fix the ambiguity integers for all the
double-differenced phase measurements of the current
epoch in the linear equation system, to minimise the
discontinuity of the RTK solutions after any phase
breaks. However, one can also define the TTAF based on
the partial ambiguity resolution (PAR) concept
developed by Teunissen (1999). The question is wether
the DD phase measurements with partially resolved
ambiguities are sufficient for PE to support the RTK
services.
AR fixed rate. This instantaneous performance
characteristic is defined as the fixed rates of the integer
estimation results. The system may be unavailable for
AR, when the geometry is too week, or satellites in view
are too few, or the effects of various errors are too
strong. AR fixed rate can be calculated by the ratio of the
total number of fixed DD integers to the total number of
DD integers over a continuously operating session. The
fixed integers are these that have passed the validation
tests in the integer search process. The problem is that
the validation process may include incorrect integers and
exclude correct integers. This parameters can be
provided by a RTK processing unit.
AR reliability (AR success rate). This is defined as the
percentage of the total correctly fixed DD integers over
the total number of DD integers. In some studies, the AR
success rate was implicitly defined as the total number of
epochs, when all the ambiguity integers are correctly
fixed, with respect to the total number of epochs of the
data session.
The other concern is the performance of RTK
positioning with the ambiguities-resolved double-
differenced (DD) phase measurements. To this end, the
RTK position estimation is similar to the code-based
SPP solutions. Therefore, we can similarly introduce the
SPP performance parameters to define the performance
of the RTK solutions:
RTK accuracy. This is defined as the degree of
conformance of an estimated RTK position at a given
time to a defined reference coordinate value (or ‘true’
value) which is obtained from an independent approach,
preferably at higher level of accuracy. As usual, the RTK
accuracy can be specified versus the rover-base
distances, for instance, σ=1.0 cm + 0.5 ppm.
RTK availability (in term of accuracy). This is defined
as the percentage of time during which the RTK
solutions are available at a certain accuracy using the
ambiguity-fixed and/or ambiguity-float phase
measurements.
RTK availability (in term of AR reliability). This
characteristic is be defined as the percentage of time, of
which PE is based on all the phase measurements whose
integers have been correctly fixed at each epoch,
assuming all the ambiguity-fixed solutions will give
required accuracy.
RTK integrity. This relates to the confidential level that
can be placed in the information provided by the RTK
system. It includes the ability of the RTK navigation
system to provide timely and valid warnings to users
when the system must not be used for the intended
operation. For instance, the RTK system with the
integrity capacity can inform users when the actual
positional errors of the RTK solutions have exceeded
Horizontal/Vertical Protection Levels (HPL/VPL) within
a certain Time-To-Alert (TTA) period at a given
Integrity Risk (IR). RTK Integrity Risk is defined as the
probability that the system claims its normal operational
status while actually being in an abnormal status, e.g.,
the ambiguities being incorrectly fixed and positional
errors having exceeded the given HPL.
RTK continuity. This is defined as RTK availability
over a certain operational period and conditions. Both

Feng et al: GPS RTK Performance Characteristics and Analysis 4
TTAF and AR availability will affect the RTK
continuity. This parameter is provided to address user
requirement for the tolerable service down-time over a
certain operational period, such as 24 hours and 7 days.
For instance in mining and civil construction, user
tolerable down-time is about 1 to 2 minutes per day,
corresponding a 99.9% of continuity requirement of
services (Positioning one consulting, 2008).
Those parameters may be either all or selectively used to
evaluate performance of a RTK system, although
variations and modifications to these definitions are still
possible. Of these parameters, the base-rover distance,
time to ambiguity fix, AR reliability, RTK availability
and RTK accuracy may be of most concerns to most
professional users. The concept of RTK integrity is also
important from the liability-critical users’ perspective. In
farming machine automation applications, the HPL is
about 10 centimetres while for civil construction
machine automation, the requirement for VPL would be
as high as a few centimetres ((Positioning one consulting,
2008). However, few existing commercial RTK systems
provide sufficient performance parameters in their
specifications. Obviously, more detailed performance
information would indeed help the users choose a
desirable RTK system to meet the performance
requirements, including integrity requirements.
3. Linear equations for ambiguity resolution
with wide-lane and narrow-lane phase
measurements
For a typical single-base RTK problem, the standard
linearised observation equations for the n×1 double-
differenced pseudoranges P1 (or C/A) and P2, carrier
phases L1 and L2 can be written as follows (Misra and
Enge, 2004)
⎥
⎥
⎥
⎥
⎦
⎤
2L
1L
2P
1P
ρ
X
L2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ε
ε
ε
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
λ−λ
λ−λ−δ
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
δ
δ
δ
−
−
−−
−−
−
−
)1,1(L
)3,4(L
)1,1(P
2
1
)1,1()1,1(
)3,4()3,4(
)1,1(
)3,4(
1,1
N
N
II
II
00
X
A
A
A
L
L
P
)1,1(
P
⎢
⎢
⎢
⎢
⎣
⎡
ε
ε
ε
ε
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
λ
λ
−δ
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
ρ−
ρ−
ρ−
ρ−
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
δ
δ
δ
δ
2
1
2
1
2
1
2
1
2
1
2
1
N
N
I0
0I
00
00
X
A
A
A
A
L
L
P
P
L
L
P
P
(1)
where is the n×1 computed double-differenced range
vector; A is the n×3 observational matrix; δis the 3×1
user state vector; the carrier phases L1 and L2; have the
wavelengths λ1 and λ2 and the integer ambiguities
and respectively; εp1, εp2, εL1 and εL2 are the noise
vectors for the respective measurement vectors
,and .
1
N
1
Pδ
2
N
2
Pδδ 1Lδ
Feng and Rizos (2007) and Feng (2008) suggested the
use of the Wide-Lane (WL) L(1,-1) and Narrow-Lane (NL)
L(4,-3) instead, in order to minimise the effects of the
larger ionospheric errors for AR over longer ranges.
P(1,1)= (f1P1+f2P2)/(f1+f2); (2)
L(1,-1) =(f1L1-f2L2)/(f1-f2); (3)
L(4,-3) =(4f1L1-3f2L2)/(4f1-3f2); (4)
where f1 and f2 stand for the frequencies for L1 and L2
carrier respectively. In (2) to (4), the subscript (i, j)
represents the integer values of the coefficients of the
combined measurements. L(1,-1) and L(4,-3) have the
wavelengths of λ(1,-1)=86.2 cm, and λ(4,-3)=11.45 cm,
respectively. As a result, we have the following linear
equations,
(5)
)3,4(
L− where
δ
,
δ
and are the residual
vectors between the observed and computed range vector
)1,1(
L− δ
ρ
or the n×1 double-differenced P(1,1), L(1,-1) and L(4,-3)
measurement vectors; I is the n×n identity matrix; εp1,1,
εL(1,-1), εL(4,-3), are the noise vectors for P(1,1), L(1,-1) and
L(4,-3) measurements, respectively. n=k-1 where k is the
number of satellites used in computation.
For convenience, Equations (1) and (2) are rewritten as
follows,
jjjjjj NBXAY
δ
=
δ
+
+
ε
(6)
12
)(;0)( − == jjj WVarE σεε (7)
where the subscript j represents the jth epoch; δY is the
m×1 observation vector; A is the m×3 matrix; δX is the
3×1 state vector; and B is the m×p matrix, N is the p×1
ambiguity vector; in which m=3(k-1) and p=2(k-1) with
dual-frequency GPS measurements.
The above equations are provided for each measurement
epoch, implying that the state and ambiguity parameters
are estimated and fixed with the measurements at the
current epoch only, which yields desirable kinematic
position solutions without imposing the assumptions of
phase measurement continuity and sample intervals.
Modelling is always the first key process for a RTK
system. This includes the processes of combining and
differencing measurements, imposing constraints such as
known coordinates and integers, applying ionosphere
and troposphere corrections etc. The stochastic models
(7) give the statistical knowledge or assumptions on the
residual errors and measurement noises, such as zero

Feng et al: GPS RTK Performance Characteristics and Analysis 5
mean white noise, correlations between the
measurements of different epochs (Wang, 2000; Wang et
al., 2002)
The next key process is to complete AR and PE
following one of the AR methods, such as the Least-
squares ambiguity decorrelation adjustment (LAMBDA)
method (Teunissen, 1995; Teunissen et al., 1997),
Minima Search (LMS) method (Pratt et al., 1997). Any
improved version of the methods will be an additional
advantage. The process basically consists of a Least-
Squares estimator and an Integer Search Engine. The
estimator provides initial real values for both state
parameters and ambiguity parameters and their
covariance matrix for the AR integer search, and then
final PE after ambiguities are fixed to their correct
integer values. The integer search engine performs a
statistical search over the potential ambiguity candidates
to find and validate the best set of integer candidates.
Implementation of efficient multipath mitigation
approaches, quality control and quality assurance
procedures in the above modeling and estimation
processing is also important. It is fairly the case that the
success of a RTK system depends on detailed processing
techniques. Some software systems implement a more
efficient integer search algorithm, whilst others are
superior in deterministic and/or stochastic modeling. The
most successful AR software takes good care of the
detailed elements, this being especially true in the
current GPS system, where only L1 and L2 carriers are
available for AR.
4. Performance Analysis of Experimental RTK
Solutions
This section will provide numeral analysis results for the
performance of RTK solutions obtained from a
commercial RTK system and the new algorithms
described in Section 3, according to the performance
characteristics defined in Section 2.
4.1 HD-RTK2TM Performance
A commercial RTK system, HD-RTK2TM, developed by
HandyNav Inc (HandyNav, 2005), was provided to the
first author for this performance analysis, so that we can
demonstrate some of the performance parameters and
how the different parameters are obtained through
experiments and are related to each other. Using two
NovAtel OEM4 receivers, the GPS testing data were
collected for seven static baselines over 2.5 to 31
kilometres in Brisbane and processed using the HD-
RTK2TM software.
Fig. 2 shows the TTFF (seconds) versus the baselines in
km in the above tests. The RTK standard deviation (STD)
accuracy in horizontal and vertical direction is illustrated
in Fig. 3, confirming the formal horizontal and vertical
accuracy within 1cm+0.5ppm and 2cm+1ppm
respectively.
0
5
10
15
20
25
30
35
40
45
50
0510 1520 2530 35
Basel i ne ( km )
TTFF (second)
Fig. 2 TTFF (seconds) plotted against baseline lengths
Thanks to HandyNav (2005), we were also able to
examine AR availability and AR reliability against
different baselines. The GPS data sets were obtained
from 16 static baselines over 2 to 45 kilometres from 60
to 400 hours. Each data set was processed separately
every 300 seconds, producing over 250,000 sets of
results and solutions. Therefore the AR availability and
reliability results can more definitively represent the
performance characteristics of the tested RTK system.
0.06
05 10 15 20 25 3035
0
0.01
0.02
0.03
0.04
0.05
Baseline (km)
Positional S TD value (m )
Nor t h
East
Up
1cm+0.5ppm
2cm+1ppm
Fig. 3 RTK positioning (STD) accuracy vs base-rover
distances
Fig. 4 illustrates the AR availability varying with
baseline lengths, while Fig. 5 plots the AR reliability
against the baseline length, showing the difference and
similarity between the two indicators. We see that AR
reliability is not necessarily worse than AR availability.
But, in general, the longer the baseline is, the lower the
AR availability and AR reliability are.

Feng et al: GPS RTK Performance Characteristics and Analysis 6
Fig. 4 AR availability variation Vs base-rover distances
In summary, with these extensive experimental results,
we conclude that the HD-RTM2TM system can provide
instant RTK solutions for distance of up to 20 km, and
ambiguity-fixed solutions for distance of up to 50km.
The AR reliability of the fixed solutions is above 99%
for 20km baselines and 98% for 50 km baselines. The
position accuracy for integer-fixed solutions is
1cm+0.5ppm (horizontal) and 2cm+1pmm (vertical). It
is believed that these performance specifications would
be more convincing to users than the specifications given
in the most commercial RTK systems
Fig. 5 AR reliability variation Vs base-rover distances.
4.2 Performance Analysis of Proposed RTK
Models and Algorithms
Using the research version of the QUT-RTK software,
we are able to test performance of different models,
algorithms and statistical conditions and processing
strategies in terms of various characteristics defined in
Section 2. In this context, we examine the performance
advantages of the model (5), using the WL L(1,-1) and NL
L(4,-3), with respect to the model (1), using L1 and L2
signals directly. Theoretically, the AR with the model (5)
may perform better than the model (1) when over longer
baselines where the effects of ionospheric delay is
minimized with respect to the wavelengths, as
demonstrated in Feng and Rizos (2007) and Feng (2008).
We now examine the AR and positioning estimation (PE)
performance using data sets of three different baselines.
In principle, this advantage may be more evident for
longer baseline and when the AR is performed instantly
with measurements from single epochs. Hence, the
following experimental results will focus on a few key
performance parameters such as AR reliability and RTK
availability and RTK accuracy, based on single-epoch
ambiguity resolution.
Three 24-h GPS data sets were collected on 1 January
2007 from US Continuously Operating Reference
Stations network (http://www.ngs.noaa.gov/CORS). All
three baselines are South-North directions, sampled at 15
second intervals.
Tables 1 and 2 summarise the performance statistical
results obtained with the models (1) and (2),
respectively, for three baselines of 21, 56 and 74 km. It
is noted that the AR reliability and RTK availability of
the model (1) are evidently higher than those of the
model (2), especially for the longer baselines. It is
important to note that the above performance results are
obtained purposely to reflect the benefits of a new
algorithm under the same circumstance and do not
represent the potential performance of the RTK system
in use. In fact, we have intentionally removed some
modelling process like known integer constraints and
advanced stochastic modelling procedures, which could
change the AR and RTK performance results. On the
other hand, the proposed characteristics may also be
effective to assess different stochastic models and
particular processing strategies, similarly through
extensive numerical studies.
Table 1 Performance results of the model (5), with WL
L(1,-1) and NL L(4,-3) observables for three baselines
P478-
P474
21km
P473-P478
56km
P473-474
74km
Total No of epochs 5760 5760 5758
Number of epochs
with wrong integers
82 727 1309
Number of DD phase
measurements
72562 72452 72310
Number of wrong
WL/NL integers
12/180 134/2487 143/4668
AR success rates for
WL/NL signals
Overall(average)
99.97%
99.50%
99.74%
99.63%
93.13%
96.38%
99.60%
87.09%
93.35%
RTK availability
(correct integer-fix)
98.58% 87.38% 77.27%
RTK availability
(0.025,0.025,0.05cm)
98.44%
99.79%
94.53%
84.81%
90.73%
90.90%
68.41%
84.00%
77.56%
RTK accuracy (STD
in North
East and Up (m)
0.008m
0.006m
0.025m
0.009m
0.007m
0.020m
0.009m
0.008m
0.030m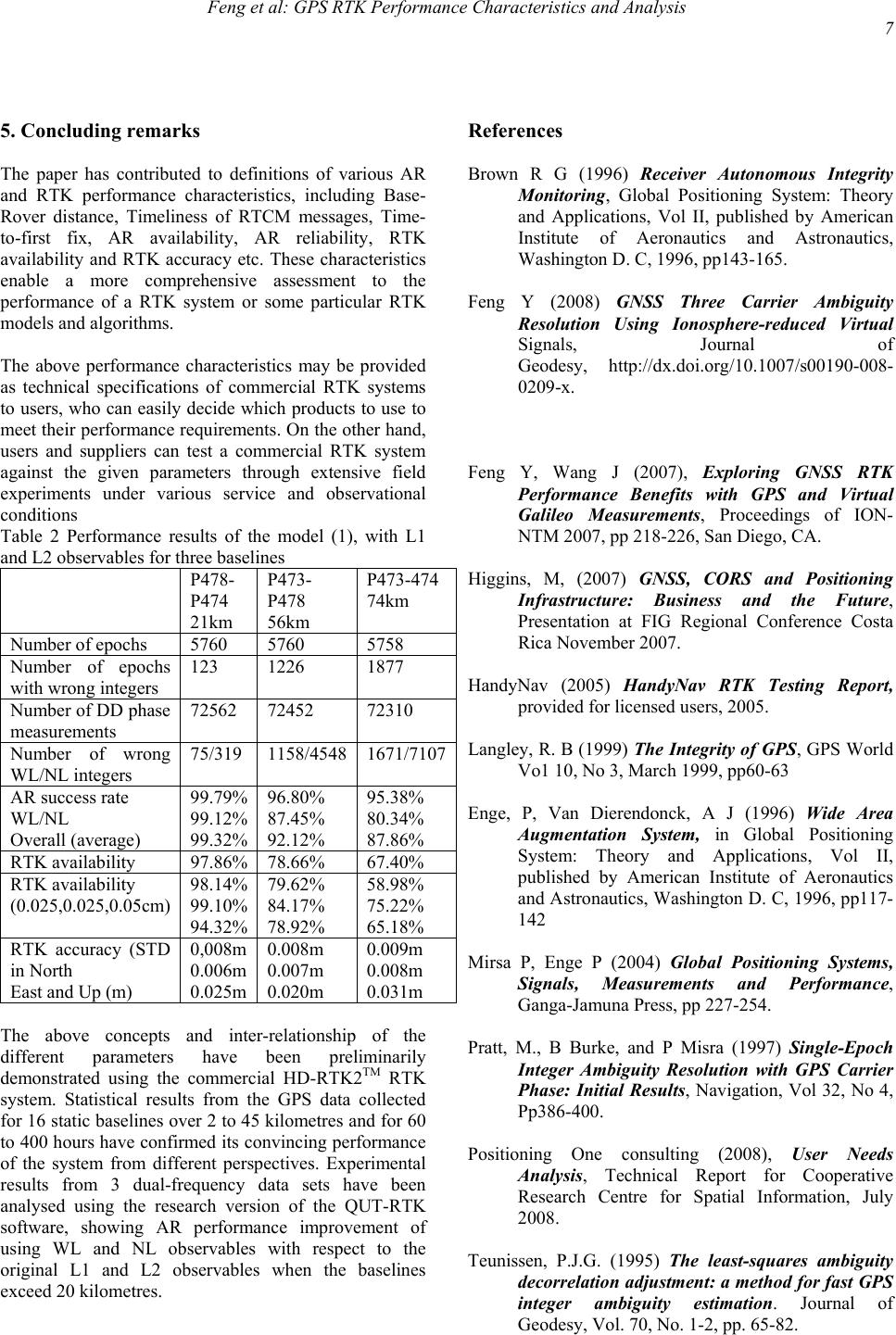

Feng et al: GPS RTK Performance Characteristics and Analysis 7
5. Concluding remarks
The paper has contributed to definitions of various AR
and RTK performance characteristics, including Base-
Rover distance, Timeliness of RTCM messages, Time-
to-first fix, AR availability, AR reliability, RTK
availability and RTK accuracy etc. These characteristics
enable a more comprehensive assessment to the
performance of a RTK system or some particular RTK
models and algorithms.
The above performance characteristics may be provided
as technical specifications of commercial RTK systems
to users, who can easily decide which products to use to
meet their performance requirements. On the other hand,
users and suppliers can test a commercial RTK system
against the given parameters through extensive field
experiments under various service and observational
conditions
Table 2 Performance results of the model (1), with L1
and L2 observables for three baselines
P478-
P474
21km
P473-
P478
56km
P473-474
74km
Number of epochs 5760 5760 5758
Number of epochs
with wrong integers
123 1226 1877
Number of DD phase
measurements
72562 72452 72310
Number of wrong
WL/NL integers
75/319 1158/4548 1671/7107
AR success rate
WL/NL
Overall (average)
99.79%
99.12%
99.32%
96.80%
87.45%
92.12%
95.38%
80.34%
87.86%
RTK availability 97.86% 78.66% 67.40%
RTK availability
(0.025,0.025,0.05cm)
98.14%
99.10%
94.32%
79.62%
84.17%
78.92%
58.98%
75.22%
65.18%
RTK accuracy (STD
in North
East and Up (m)
0,008m
0.006m
0.025m
0.008m
0.007m
0.020m
0.009m
0.008m
0.031m
The above concepts and inter-relationship of the
different parameters have been preliminarily
demonstrated using the commercial HD-RTK2TM RTK
system. Statistical results from the GPS data collected
for 16 static baselines over 2 to 45 kilometres and for 60
to 400 hours have confirmed its convincing performance
of the system from different perspectives. Experimental
results from 3 dual-frequency data sets have been
analysed using the research version of the QUT-RTK
software, showing AR performance improvement of
using WL and NL observables with respect to the
original L1 and L2 observables when the baselines
exceed 20 kilometres.
References
Brown R G (1996) Receiver Autonomous Integrity
Monitoring, Global Positioning System: Theory
and Applications, Vol II, published by American
Institute of Aeronautics and Astronautics,
Washington D. C, 1996, pp143-165.
Feng Y (2008) GNSS Three Carrier Ambiguity
Resolution Using Ionosphere-reduced Virtual
Signals, Journal of
Geodesy, http://dx.doi.org/10.1007/s00190-008-
0209-x.
Feng
f ION-
NTM 2007, pp 218-226, San Diego, CA.
Higgin
egional Conference Costa
Rica November 2007.
Handy esting Report,
provided for licensed users, 2005.
Langl , GPS World
Vo1 10, No 3, March 1999, pp60-63
Enge,
stronautics, Washington D. C, 1996, pp117-
142
Mirsa Performance,
Ganga-Jamuna Press, pp 227-254.
Pratt,
l Results, Navigation, Vol 32, No 4,
Pp386-400.
Positio
ch Centre for Spatial Information, July
2008.
Teuni
urnal of
Geodesy, Vol. 70, No. 1-2, pp. 65-82.
Y, Wang J (2007), Exploring GNSS RTK
Performance Benefits with GPS and Virtual
Galileo Measurements, Proceedings o
s, M, (2007) GNSS, CORS and Positioning
Infrastructure: Business and the Future,
Presentation at FIG R
Nav (2005) HandyNav RTK T
ey, R. B (1999) The Integrity of GPS
P, Van Dierendonck, A J (1996) Wide Area
Augmentation System, in Global Positioning
System: Theory and Applications, Vol II,
published by American Institute of Aeronautics
and A
P, Enge P (2004) Global Positioning Systems,
Signals, Measurements and
M., B Burke, and P Misra (1997) Single-Epoch
Integer Ambiguity Resolution with GPS Carrier
Phase: Initia
ning One consulting (2008), User Needs
Analysis, Technical Report for Cooperative
Resear
ssen, P.J.G. (1995) The least-squares ambiguity
decorrelation ad justment: a method for fast GPS
integer ambiguity estimation. Jo

Feng et al: GPS RTK Performance Characteristics and Analysis 8
Teuni
esolution, Navigation,
Vol 44, No 3, pp373-383.
Teuni
TM 1999, pp
201-207, Jan 25-27, San Diego CA
Walte
f Global
Wang
f
the US Institute of Navigation, 46(4), 297-305
Wang
e positioning, Journal of
Geodesy, 76(2), 95-104
ssen, P.J.G, P J De Jonge and C.C. J.M Tiberious
(1997). Performance of the LAMBDA Method
for fast GPS Ambiguity R
ssen PJG, Joosten P, Tiberius C.C.J.M (1999)
Geometry-free ambiguity success rates in case of
partial fixing. Proceedings of ION-N
r, T. (2002) Introduction to the Wide Area
Augmentation System, Journal o
Positioning Systems 1(2), pp151-153.
J. (2000) Stochastic modelling for RTK
GPS/Glonass positioning, Navigation, Journal o
J., C. Satirapod & C. Rizos (2002) Stochastic
assessment of GPS carrier phase measurements
for precise static relativ