O. A. RYABUSHKIN ET AL. 27
here m is crystal mass, c is specific heat capacity, S is
crystal surface area. Optical absorption coefficient is cal-
culated as follows
() T
LhS
. (8)
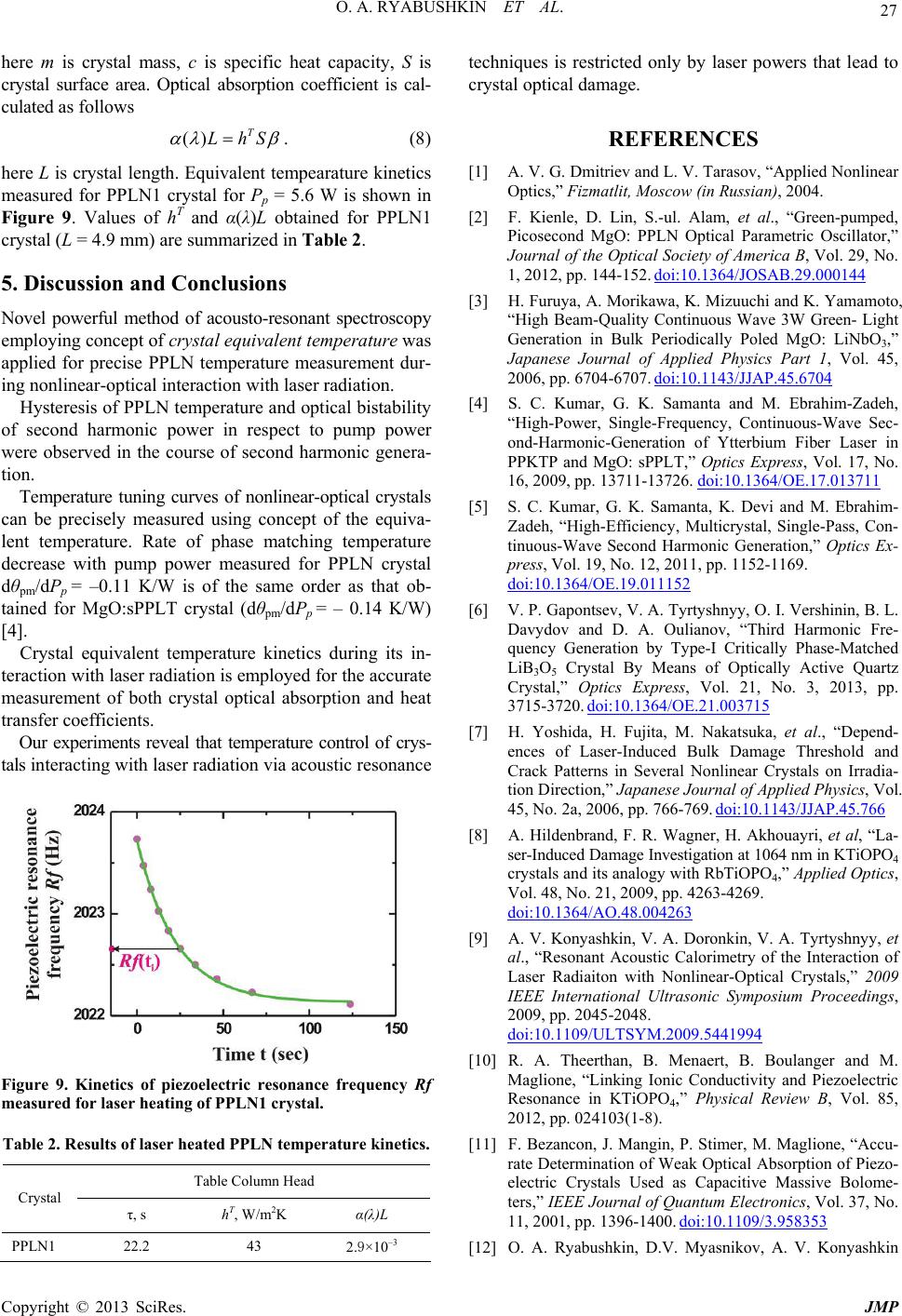
here L is crystal length. Equivalent tempearature kinetics
measured for PPLN1 crystal for Pp = 5.6 W is shown in
Figure 9. Values of hT and α(λ)L obtained for PPLN1
crystal (L = 4.9 mm) are summarized in Table 2.
5. Discussion and Conclusions
Novel powerful method of acousto-resonant spectroscopy
employing concept of crystal equivalent temperature was
applied for precise PPLN temperature measurement dur-
ing nonlinear-optical interaction with laser radiation.
Hysteresis of PPLN temperature and optical bistability
of second harmonic power in respect to pump power
were observed in the course of second harmonic genera-
tion.
Temperature tuning curves of nonlinear-optical crystals
can be precisely measured using concept of the equiva-
lent temperature. Rate of phase matching temperature
decrease with pump power measured for PPLN crystal
dθpm/dPp = –0.11 K/W is of the same order as that ob-
tained for MgO:sPPLT crystal (dθpm/dPp = – 0.14 K/W)
[4].
Crystal equivalent temperature kinetics during its in-
teraction with laser radiation is employed for the accurate
measurement of both crystal optical absorption and heat
transfer coefficients.
Our experiments reveal that temperature control of crys-
tals interacting with laser radiation via acoustic resonance
Figure 9. Kinetics of piezoelectric resonance frequency Rf
measured for laser heating of PPLN1 crystal.
Table 2. Results of laser heated PPLN temperature kinetics.
Table Column Head
Crystal
τ, s hT, W/m2K α(λ)L
PPLN1 22.2 43 2.9×10–3
techniques is restricted only by laser powers that lead to
crystal optical damage.
REFERENCES
[1] A. V. G. Dmitriev and L. V. Tarasov, “Applied Nonlinear
Optics,” Fizmatlit, Moscow (in Russian), 2004.
[2] F. Kienle, D. Lin, S.-ul. Alam, et al., “Green-pumped,
Picosecond MgO: PPLN Optical Parametric Oscillator,”
Journal of the Optical Society of America B, Vol. 29, No.
1, 2012, pp. 144-152. doi:10.1364/JOSAB.29.000144
[3] H. Furuya, A. Morikawa, K. Mizuuchi and K. Yamamoto,
“High Beam-Quality Continuous Wave 3W Green- Light
Generation in Bulk Periodically Poled MgO: LiNbO3,”
Japanese Journal of Applied Physics Part 1, Vol. 45,
2006, pp. 6704-6707. doi:10.1143/JJAP.45.6704
[4] S. C. Kumar, G. K. Samanta and M. Ebrahim-Zadeh,
“High-Power, Single-Frequency, Continuous-Wave Sec-
ond-Harmonic-Generation of Ytterbium Fiber Laser in
PPKTP and MgO: sPPLT,” Optics Express, Vol. 17, No.
16, 2009, pp. 13711-13726. doi:10.1364/OE.17.013711
[5] S. C. Kumar, G. K. Samanta, K. Devi and M. Ebrahim-
Zadeh, “High-Efficiency, Multicrystal, Single-Pass, Con-
tinuous-Wave Second Harmonic Generation,” Optics Ex-
press, Vol. 19, No. 12, 2011, pp. 1152-1169.
doi:10.1364/OE.19.011152
[6] V. P. Gapontsev, V. A. Tyrtyshnyy, O. I. Vershinin, B. L.
Davydov and D. A. Oulianov, “Third Harmonic Fre-
quency Generation by Type-I Critically Phase-Matched
LiB3O5 Crystal By Means of Optically Active Quartz
Crystal,” Optics Express, Vol. 21, No. 3, 2013, pp.
3715-3720. doi:10.1364/OE.21.003715
[7] H. Yoshida, H. Fujita, M. Nakatsuka, et al., “Depend-
ences of Laser-Induced Bulk Damage Threshold and
Crack Patterns in Several Nonlinear Crystals on Irradia-
tion Direction,” Japanese Journal of Applied Physics, Vol.
45, No. 2a, 2006, pp. 766-769. doi:10.1143/JJAP.45.766
[8] A. Hildenbrand, F. R. Wagner, H. Akhouayri, et al, “La-
ser-Induced Damage Investigation at 1064 nm in KTiOPO4
crystals and its analogy with RbTiOPO4,” Applied Optics,
Vol. 48, No. 21, 2009, pp. 4263-4269.
doi:10.1364/AO.48.004263
[9] A. V. Konyashkin, V. A. Doronkin, V. A. Tyrtyshnyy, et
al., “Resonant Acoustic Calorimetry of the Interaction of
Laser Radiaiton with Nonlinear-Optical Crystals,” 2009
IEEE International Ultrasonic Symposium Proceedings,
2009, pp. 2045-2048.
doi:10.1109/ULTSYM.2009.5441994
[10] R. A. Theerthan, B. Menaert, B. Boulanger and M.
Maglione, “Linking Ionic Conductivity and Piezoelectric
Resonance in KTiOPO4,” Physical Review B, Vol. 85,
2012, pp. 024103(1-8).
[11] F. Bezancon, J. Mangin, P. Stimer, M. Maglione, “Accu-
rate Determination of Weak Optical Absorption of Piezo-
electric Crystals Used as Capacitive Massive Bolome-
ters,” IEEE Journal of Quantum Electronics, Vol. 37, No.
11, 2001, pp. 1396-1400. doi:10.1109/3.958353
[12] O. A. Ryabushkin, D.V. Myasnikov, A. V. Konyashkin
Copyright © 2013 SciRes. JMP