Modern Economy, 2010, 1, 168-170
doi:10.4236/me.2010.13019 Published Online November 2010 (http://www.SciRP.org/journal/me)
Mathematical Model of Housing Loans
Xiangrong Li
College of Mathem at i cs an d I nf or mat ion Science, Guangxi University, Nanning, China
Received July 27, 201 0; revised August 30, 2010; accepted September 5, 2010
Abstract
Currently, that individual use housing mortgage loans to buy houses has become a hot topic, and residents
are very concerned about the debt repayment ways of individual housing mortgage loans. In this paper, using
the time value of money principle, we establish equal principal and interest repayment model. Furthermore
we test its validation and illustrate its specific application with an example in the economic life.
Keywords: Mathematical Model; Housing Mortgage Loans; Equal Principal and Interest Repayment
1. Introduction
With the development of economic and society, using
housing mortgage loans, personal buying house becomes
a more and more common phenomenon [1]. The
so-called mortgage is that consumers purchase what they
need by borrowing money from banks, at the same time,
they must mortgage what they buy to banks as collateral,
and within the agreed time, consumers should repay the
loan and pay interest in accordance with the agreed time
intervals. However, most people do not know much
about the repayment of some of the issues. We try to
reveal its contents from the mathematical model [2].
2. Modeling
2.1. Basic Assumptions
1) Repayment period is fixed;
2) Interest rates do not fluctuate;
3) Interest rate and term are calculated on a monthly
basis;
4) Each repayment is occurred at the last day of cur-
rent [3].
2.2. Equal Principal and Interest Repayment
Modeling
Set P is the loan principal, i is monthly interest rate, n is
the number of months for the repayment, and A is the
monthly repayment amount.
Using the time value of money principle, the above
economic problems can be converted into ordinary annu-
ity present value formula, that is
 
123
111 1
n
PA iA iA iA i



multiply with the same (1 + i) both sides of the equation,
then
 
 

12
31
111
11
n
PiAAi Ai
Ai Ai





2-type phase for reduction, then
 
11 ,,
n
i
PA APAin
i


 

(1)
Where,

11 n i
i

 is present value annuity factor,
denoted by


,,PAin , direct access to ‘the present
value of annuity factor table’.
2.3. Calculating the Monthly Repayment
Amount

,,
P
APAin  (2)
2.4. Calculation of the Total Interest
I
PnA

 (3)
3. Validation and Application of the Model
Table 1 is equal principal and interest rep ayment method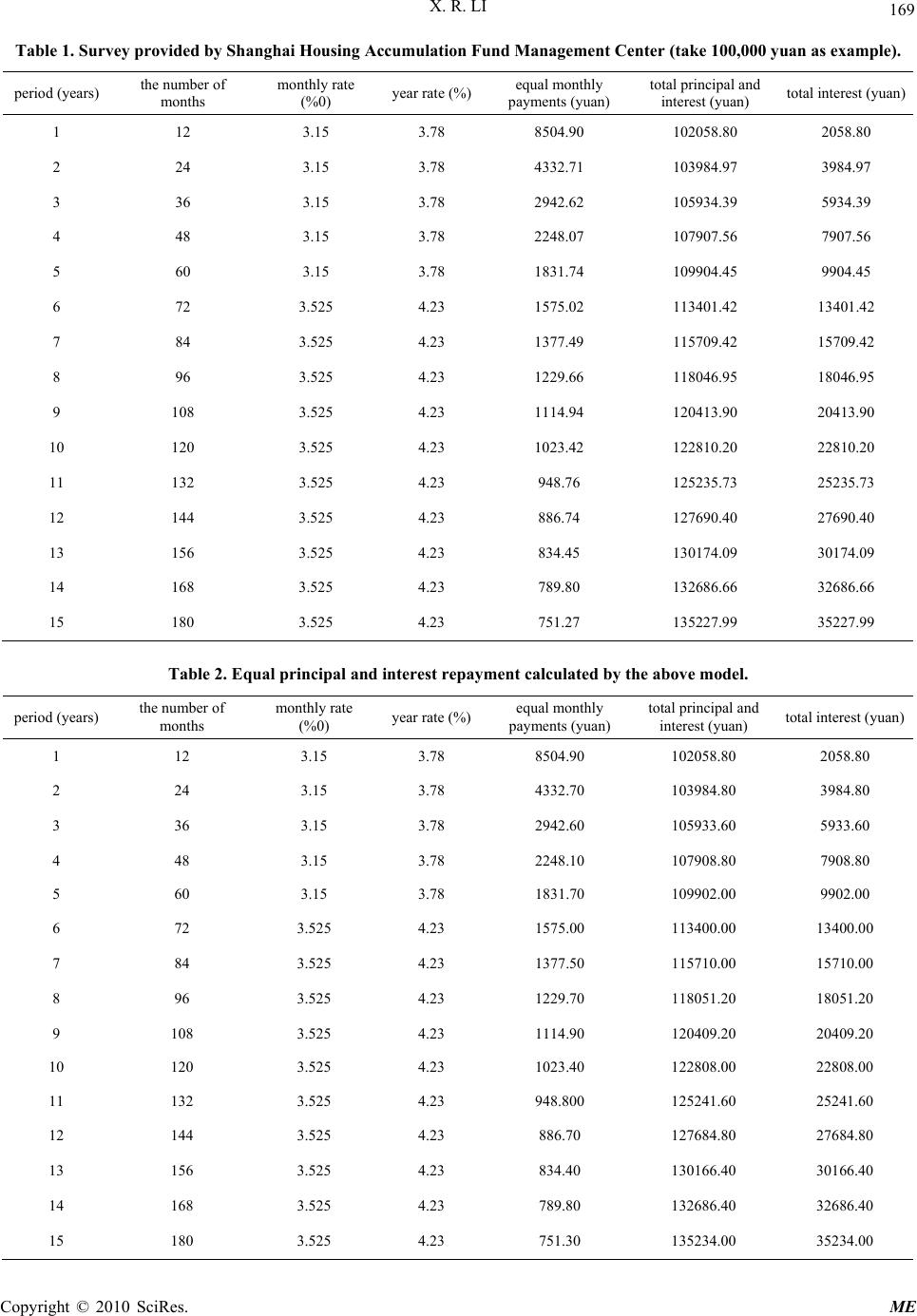

X. R. LI
169
Table 1. Survey provided by Shanghai Housing Accumulation Fund Management Center (take 100,000 yuan as example).
period (years) the number of
months monthly rate (%0) year rate (%) equal monthly payments (yuan) total principal and interest (yuan) total interest (yuan)
1 12 3.15 3.78 8504.90 102058.80 2058.80
2 24 3.15 3.78 4332.71 103984.97 3984.97
3 36 3.15 3.78 2942.62 105934.39 5934.39
4 48 3.15 3.78 2248.07 107907.56 7907.56
5 60 3.15 3.78 1831.74 109904.45 9904.45
6 72 3.525 4.23 1575.02 113401.42 13401.42
7 84 3.525 4.23 1377.49 115709.42 15709.42
8 96 3.525 4.23 1229.66 118046.95 18046.95
9 108 3.525 4.23 1114.94 120413.90 20413.90
10 120 3.525 4.23 1023.42 122810.20 22810.20
11 132 3.525 4.23 948.76 125235.73 25235.73
12 144 3.525 4.23 886.74 127690.40 27690.40
13 156 3.525 4.23 834.45 130174.09 30174.09
14 168 3.525 4.23 789.80 132686.66 32686.66
15 180 3.525 4.23 751.27 135227.99 35227.99
Table 2. Equal principal and interest repayment calculated by the above model.
period (years) the number of
months monthly rate (%0) year rate (%) equal monthly payments (yuan) total principal and interest (yuan) total interest (yuan)
1 12 3.15 3.78 8504.90 102058.80 2058.80
2 24 3.15 3.78 4332.70 103984.80 3984.80
3 36 3.15 3.78 2942.60 105933.60 5933.60
4 48 3.15 3.78 2248.10 107908.80 7908.80
5 60 3.15 3.78 1831.70 109902.00 9902.00
6 72 3.525 4.23 1575.00 113400.00 13400.00
7 84 3.525 4.23 1377.50 115710.00 15710.00
8 96 3.525 4.23 1229.70 118051.20 18051.20
9 108 3.525 4.23 1114.90 120409.20 20409.20
10 120 3.525 4.23 1023.40 122808.00 22808.00
11 132 3.525 4.23 948.800 125241.60 25241.60
12 144 3.525 4.23 886.70 127684.80 27684.80
13 156 3.525 4.23 834.40 130166.40 30166.40
14 168 3.525 4.23 789.80 132686.40 32686.40
15 180 3.525 4.23 751.30 135234.00 35234.00

X. R. LI
170
list of individual housing loan (provided by Shanghai
Housing Accu mulation Fund M a nagement Center) .
Now we will test the above model’s validation with
Table 1, then get Table 2:
The data of Table 2 and Table 1 are coincident. The
above laboratory data show that the model is more real-
istic.
4. Conclusions
See from the above results，the model is basic good. It
can meet generally the daily needs of people.
Most people know that there are many ways of mort-
gage repayment. In addition to equal principal and inter-
est repayment, there are equal principal repayment, a
debt service, equal increments and equal decrease, and so
on. Among them, the most common repayments are
equal principal and interest repayment and equal princi-
pal repayment [4].
In this paper, we only establish equal principal an d in-
terest repayment model. Other models (such as equal
principal repayment model) are yet to be established. We
will make further study of its.
5. References
[1] Y. P. Zhang and W. Q. Yuan, “Mathematical model of
mortgage loans,” Journal of Yellow River Conservancy
Technical Institute, Vol. 18, No. 1, 2006, pp.
[2] S. C. Matthew, C. Garriga and D. Schlagenhauf, “The
loan structure and housing tenure decisions in an equilib-
rium model of mortgage choice,” Review of Economic
Dynamics, Vol. 12, No. 3, 2009, pp.444-468.
[3] V. Hartarska and C. Gonzalez-Vega, “Evidence on the
effect of credit counseling on mortgage loan default by
low-income households,Journal of Housing Economics,”
Vol. 15, No. 1, 2006, pp. 63-79.
[4] A. Sumit and W. Brent, “Ambrose, Souphala Chomsis-
engphet, Chunlin Liu, An empirical analysis of home eq-
uity loan and line performance,” Journal of Financial In-
termediation, Vol. 15, No. 4, 2006, pp. 444-469.