Int'l J. of Communications, Network and System Sciences
Vol.6 No.12(2013), Article ID:40783,8 pages DOI:10.4236/ijcns.2013.612053
Improving Compression of Short Messages
Flinders University, Adelaide, Australia
Email: paul@servalproject.org, andrew@servalproject.org, romana@servalproject.org, corey@servalproject.org, jenny@servalproject.org, jeremy@servalproject.org
Copyright © 2013 Paul Gardner-Stephen et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 24, 2013; revised May 24, 2013; accepted May 30, 2013
Keywords: Lossless; Text Compression; Sms; Twitter; Arithmetic Coding; Mobile; Cellular; Mesh Network
ABSTRACT
Compression of short text strings, such as the GSM Short Message Service (SMS) and Twitter messages, has received relatively little attention compared to the compression of longer texts. This is not surprising given that for typical cellular and internet-based networks, the cost of compression probably outweighs the cost of delivering uncompressed messages. However, this is not necessarily true in the case where the cost of data transport is high, for example, where satellite back-haul is involved, or on bandwidth-starved mobile mesh networks, such as the mesh networks for disaster relief, rural, remote and developing contexts envisaged by the Serval Project [1-4]. This motivated the development of a state-of-art text compression algorithm that could be used to compress mesh-based short-message traffic, culminating in the development of the stats3 SMS compression scheme described in this paper. Stats3 uses word frequency and 3rd-order letter statistics embodied in a pre-constructed dictionary to affect lossless compression of short text messages. This scheme shows that our scheme compressing text messages typically reduces messages to less than half of their original size, and in so doing substantially outperforms all public SMS compression systems, while also matching or exceeding the marketing claims of the commercial options known to the authors. We also outline approaches for future work that has the potential to further improve the performance and practical utility of stats3.
1. Introduction
Loss-less compression is a mature field, with a wide variety of methodologies and implementations. However, compression of short strings is relatively under-explored. This is perhaps due to the relatively small gains to be made by compressing strings that are already quite short, combined with the relative difficulty of compressing strings that are so short that they have little opportunity to expose sufficient redundancy to allow for effective compression.
Thus, even for cellular Short Message Service (SMS) traffic, where message volumes are enormous, relatively little effort has been invested. The GSMA did create a standard for SMS compression, GSM 03.42 [5], but it is difficult to ascertain whether it has been widely adopted by carriers, and the standard itself has not been updated since 1999 apart from being carried forward into the corresponding LTE standard [6], even though attractive compression technologies such as Arithmetic Coding [7- 12] have lapsed from patent encumberance in the meantime. Perhaps for mobile telecommunications carriers, the disinterest is simply commercial; they charge per message unit of 160 7-bit characters, i.e., 140 8-bit bytes, and reducing the number of messages required for parties to communicate would be revenue-negative.
Of course, for consumers, the situation is different, because consumers pay carriers per message unit. The impressive cost charged per message unit by mobile telecommunications carriers, introduces the potential for SMS compression to be revenue-positive.
Indeed, the cost savings are sufficient. A number of companies have based their business model around compressed-SMS services [13-15], and claimed reductions in message sizes of between 30% - 40% [13] and 50% - 55% [14]. However, as commercial solutions, these claims cannot be easily verified nor are the source code available to allow meaningful benchmarking against other options. The advent of two-way satellite SMS services, such as the deLorme inReach that uses the Iridium constellation, has created further incentive for compression of messages, as Iridium charges the service providers a substantial fee per byte.
The desire to compress SMS and Twitter-like messages is heightened for systems such as the Serval Project where communications are encrypted and authenticated for security, introducing unavoidable and uncompressible overhead to each message in the form of digital signatures [16]. The Serval Project [2-4] is a mobile ad-hoc network that provides resilient communications for rural, remote and disaster situations. In such networks, bandwidth is often limited, and clusters of nodes may be isolated from one another, and satellite SMS services may be the backhaul of last resort.
The Serval Project offers SMS-like short messaging and Twitter-like social networking services [3]; thus the motivation for identifying effective compression schemes that can be effective on SMS-length messages of the kind was commonly observed on Twitter.
The remainder of this paper briefly explores: technical challenges to compressing short messages; a survey of existing compression schemes appropriate for use on SMS-length messages; an introduction to our new stats3 SMS compression scheme, including a comparison with the existing state-of-the-art, showing that our scheme substantially outperforms all public SMS compression systems, and matches or outperforms the unverified marketing claims of the commercial offerings. Finally, we outline several areas for future work that we believe, which have the potential to further improve the performance of stats3.
2. Challenges of Compressing of Short Messages
The longer a message, the more likely it is to contain sufficient redundancy to allow a compression scheme to encode it in a manner that results in a reduction in size. There are several reasons why compressing short messages is particularly difficult.
First, many compression schemes are adaptive, that is, they build a model of the statistics of a message as they go along, which is then used to feed a predictor that estimates the probability of following bits or bytes. Most such predictors require hundreds of characters to be processed before they are able to begin usefully to model the message, and thus begin to save space.
Second, many compression schemes, whether adaptive or not, use a dictionary that provides initial context to the predictor, precisely to avoid the slow convergence that can result from purely adaptive compression schemes. However, this introduces a substantial overhead to the beginning of the message, which for SMS-length messages may be larger than whole uncompressed message.
As a result, most compression algorithms that perform well on bulk data, e.g., gzip [17], bzip2 [18,19] and PAQ
[20], all perform poorly on short messages, as illustrated in Table 1 where the performance of each of those compressors on the individual messages of the SMAZ sample messages of Table 2 is shown.

Table 1. Uncompressed and compressed sizes of the SMAZ sample message set for several high-performance compression schemes. Smallest size for each message is underlined.

Table 2. SMAZ sample message set, as extracted from SMAZ source code.
3. Existing Short Message Compression Schemes
The logical solution to the challenge of compressing short strings such as SMS messages is to pre-compute a dictionary that then does not need to be embedded in each compressed message. This is indeed the approach taken by many extant SMS compression schemes, of which the following are perhaps the most prominent. The non-dictionary shortBWT scheme and several commercial SMS compression systems are added for completeness.
3.1. GSM TS03.42
Between 1997 and 1999 the GSM Association (GSMA) developed Technical Standard (TS) 03.42 [5,6], a standard for compression of SMS messages. At the time Arithmetic Coding was possibly patent encumbered, and perhaps for that reason and the relatively higher computation demands of that scheme, TS03.42 uses Huffman Coding [21-25], in return for a reduction in the compression possible. They begin with a language-specific frequency table and common word list to provide initial context. The frequency table is optionally evolved as a message is compressed providing some adaptability, although the word list is fixed.
The technical standard itself is accompanied by three sample SMS messages (see Table 3) and their compressed forms, giving some idea of the compression levels that it can achieve, which is summarised in Table 4.
If the sample messages are a reliable guide, the GSMA seemed to assume SMS being used for carrying longer email-like messages, and apparently by pedants for spelling and grammar, somewhat amplifying the apparent effectiveness of their scheme. Empirical examination of SMS and Twitter traffic suggests that those assumptions are flawed, and that in practice, TS03.42 would be likely to offer poorer compression than suggested by their unrepresentative, if well meaning, examples.
A more fundamental issue is that TS03.42 does not anticipate that users of SMS and Twitter-like services already employ an ad-hoc form of compression in their messages, using various forms of short hand to fit their messages into the confines of the medium, e.g., shortening words such as “before” to “b4” and “tomorrow” to “2moro”, and in doing so likely limiting the ability of TS03.42 to achieve any significant degree of compression.
Further assessment of the performance of TS03.42 is not possible without obtaining or creating an implementation of the relatively intricate specification, which are outside the scope of this paper. Thus assigning an estimation of the performance of TS03.42 on real SMS and Twitter traffic is difficult, with performance not likely to


Table 3. GSMA TS03.42 Example SMS Messages. Note that the apparently erroneous repetition of 021 appears in the file downloaded from the GSMA.

Table 4. Uncompressed and GSM TS03.42 and SMAZ compressed sizes of the TS03.42 example messages. Percentages are versus original size (lower is better).
be better than reducing message sizes to 50% of original size on average. Relative performance can be inferred by comparing the relative performance on the three TS03.42 sample SMS messages. For example, Table 4 gives us reason to believe that TS03.42 outperforms SMAZ by a considerable margin.
3.2. SMAZ
SMAZ [26] is the only other open-source short-message compression library known to the authors. SMAZ is remarkable in that its complete implementation is less than 200 lines of code—which includes the code book of common character sequences that performs the role of the pre-computed dictionary. The README file for SMAZ claims average reduction in message length to 50% - 60% of original size, with English text compressing better.
The performance of SMAZ on the three English text TS03.42 sample messages suggests that the claim of reducing messages to an average of 50% - 60% of original size may not hold true for SMS-type traffic. As the implementation of SMAZ is freely available it is possible to test this claim.
See Table 5 for a summary of SMAZ performance on a variety of inputs. Attempt was made to include the National University of Singapore (NUS) SMS corpus, the largest public SMS corpus known to the authors. The NUS corpus custodians did not respond in time for inclusion of the NUS corpus in this comparison. SMS SPAM Collection v.1 [27] consists of (at the time) approximately 37% of the NUS corpus. All NUS SMS corpus derived corpora will be necessarily biased because the majority of messages were obtained from students at the NUS.
| 2http://trec.nist.gov/data/tweets/; on-line; accessed 15 November 2012. |
The Private Twitter Corpus is a collection of Twitter messages collected in several episodes during October and November 2012. Collection occurred using the Twitter statuses/sample API that returns a random sampling of public Twitter status messages1, and filtered to exclude all messages containing unicode characters, as efficient handling of unicode messages is beyond the scope of the work described in this paper. Nonetheless,

Table 5. SMAZ compression performance for various inputs: compressed size as percentage of original size (lower is better).
*The text from http://en.wikipedia.org/wiki/Pie_floater.
the corpus contains messages in many languages and of a wide variety of forms. Twitter’s terms of use appear to prevent the release of any public corpus of Twitter messages, and even the TREC community is only able to distribute a list of tweets, rather than the tweets themselves2. Benchmarking against the 93 million message TREC Twitter Corpus [29] is beyond the scope of this paper, as such a large corpus is not necessary to obtain meaningful statistics about composition and compressibility of Twitter messages.
Overall for SMAZ, observed average compressed message lengths were all worse than the claimed range for English text, and in the case of Twitter messages much worse, with average compressed message lengths of 81.4% of the uncompressed message length. Thus, while effective in many instances, SMAZ elegantly small dictionary-based approach is not sufficiently robust in the face of Twitter type traffic.
3.3. ShortBWT
The shortBWT [30] scheme is included as a counterpoint, based on the remarkable properties of the Burrows-Wheeler transform [18], and can be generally understood as the equivalent of bzip2 [19] for short strings. In contrast with SMAZ and TS03.42, shortBWT does not use a precomputed dictionary of words or word parts, but rather uses precomputed statistics for the relative diversity and abundance of characters in a message.
As shortBWT does not appear to be publicly avaiable, its performance can only be estimated by examining Constantinescu et al. (2004) [30]. That paper suggests shortBWT is capable of compressing strings of 200 characters to an average of around 55% of their original size. Performance on shorter strings is impossible to discern from their paper, but there is no reason to believe that performance would be any better on shorter strings, as shorter strings make it more difficult for the Burrows-Wheeler transform to find the redundancy necessary to effect compression.
3.4. Commercial Short Message Compression Systems
There are several commercial SMS compression schemes available, e.g. [13-15]. As closed-source proprietary offerings, there is limited information as to their operation. However, for the purposes of this paper our focus is on compression performance. The two commercial offerings which make claims about the compression performance of their products make claims of reductions in message sizes to between 60% - 70% [4] and 45% - 50% [14] of the original message length. Assuming that their claims are not exaggerated, this implies similar performance to shortBWT. However, as with SMAZ, it is likely that either limited testing or other processes have resulted in a claim that is not sustained when faced with realistic SMS or Twitter traffic.
3.5. Summary
The state of the art of short message compression can be summarised as the various solutions offering compressed message sizes which are, on average, at least 45% of the uncompressed message size, although, as previously explained, there is reason to doubt that performance is in fact that good. SMAZ is the only openly available scheme, and it performs much more poorly than the best claims among the closed systems. Thus there is, in the very least, the opportunity to match, or beat, the best closed systems through the creation of a new open-source short message compression scheme. The following section describes the process by which we achieved this goal, culminating in the implementation of the stats3 short-message compression scheme.
4. Overview of the Stats3 Short Message Compression Scheme
It was decided that the most promising approach was to model the statistics of a corpus of representative Twitter messages and use that as a basis for a non-adaptive compression scheme, using arithmetic coding for the back end.
4.1. Character Statistics Generation & Encoding of Mono-Case Textual Characters
A corpus of Twitter messages was obtained as previously described in this paper. A program was written to analyse those messages at the character level to determine the probability of the first letter of a message being either upper or lower case, and to compute the 1st, 2nd and 3rd order statistics for:
1) the probability of the 69 most commonly occurring characters, treating all letters as lower case;
2) the probability of the first letter in a word being upper or lower case, based on the case of the previous word(s) as appropriate;
3) the probability of each letter in a word being upper or lower case, based on the case of the previous letters in the word.
4) the probability of messages being of any particular length between 0 and 1,024 characters, the maximum length of short message supported by stats3.
Messages were stripped of all letter-case information and non-textual characters and then encoded according to the 3rd order statistics. The length of the uncompressed message was encoded according to the message length statistics. The case of letters was compressed by, for each letter in a message, using the 3rd-order case statistics gathered to predict the case of that letter.
4.2. Dictionary Generation
In addition, word-level analysis was performed, using all characters other than a - z and 0 - 9 to indicate a word break. All words occurring less than five times were discarded. Whenever a word was discarded, it was attempted to assign the frequency to another word sharing the longest common prefix with the discarded word. For example, discarding four instances of “bakfietsen” would result in the recorded frequency of “bakfiets” to increase by four.
The entropy of the each word remaining in the list was modelled using the 3rd order statistics previously computed, resulting in an estimate of the number of bits required to encode the word as a sequence of characters. This represents the saving possible by encoding the word as a single token .
.
The number of instances of all remaining words was calculated, as was the total number of word breaks in the corpus. From this it was possible to compute the probability of a word substitution occurring at any single word break, and from that the entropy, and hence the bit cost of either substituting or not substituting. Substitution occurred with , thus a no-substitution event could be encoded in less than one bit. For the same reason, each word substitution event must incur a cost per substitution
, thus a no-substitution event could be encoded in less than one bit. For the same reason, each word substitution event must incur a cost per substitution 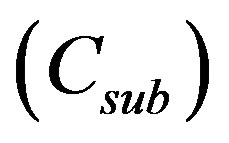 of ≥1 bit. That cost must be deducted from the savings possible by substituting each word. The cost of encoding any given word
of ≥1 bit. That cost must be deducted from the savings possible by substituting each word. The cost of encoding any given word  can be computed from the relative frequency of that word in the training corpus. Thus the overall saving per word when substituted could be estimated according to
can be computed from the relative frequency of that word in the training corpus. Thus the overall saving per word when substituted could be estimated according to  .
.
 was calculated for each word remaining in the list. Any words where
was calculated for each word remaining in the list. Any words where  were discarded from the list, and
were discarded from the list, and 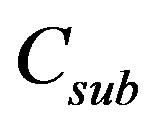 was then recalculated. This process was repeated until no further words were removed from the list. A side effect of this process is that the word list contains no low-entropy words, as they are more efficiently encoded directly using the 3rd order statistics. For example, “the” is not in the list despite its high frequency, while words such as “tomorrow” (and numerous misspellings thereof) are in the list, because of the higher entropy of that word. From a corpus of 203,661 of Twitter messages a list of 13,179 substitutable words was produced.
was then recalculated. This process was repeated until no further words were removed from the list. A side effect of this process is that the word list contains no low-entropy words, as they are more efficiently encoded directly using the 3rd order statistics. For example, “the” is not in the list despite its high frequency, while words such as “tomorrow” (and numerous misspellings thereof) are in the list, because of the higher entropy of that word. From a corpus of 203,661 of Twitter messages a list of 13,179 substitutable words was produced.
4.3. Rare & Non-Text Characters
Characters that were not in the 69 common characters that are covered by the predictive model were exceptionally rare. While a more refined method is possible, the current implementation encodes those characters in a two part process. First, an interpolative coder [31] using an arithmetic coding back-end was used to efficiently encode the positions of the characters in the message. The actual characters were then recorded using arithmetic coding.
4.4. Model Selection
In addition to the model described above, two simpler models were also included for instances where the pre-computed statistics resulted in the compressed message being longer than the uncompressed message.
First, if no rare or non-textual characters were present in the message, the entire message was encoded using radix-69. Case information was still encoded as for the statistical model. Selection of this model versus the statistical model is via a single decision with , resulting in a cost of 0.074 bits to use the statistical model and a cost of 4.322 bits to use this non-statistical model. A more accurate assessment would place
, resulting in a cost of 0.074 bits to use the statistical model and a cost of 4.322 bits to use this non-statistical model. A more accurate assessment would place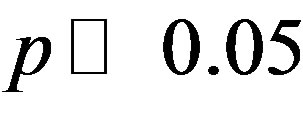 , but would also result in a substantially higher bit cost to use the non-statistical model, without offering any significant reduction in cost overall.
, but would also result in a substantially higher bit cost to use the non-statistical model, without offering any significant reduction in cost overall.
Second, if rare or non-textual characters were present, and the MSB of the first character was zero, the message was encoded as the identical of the input string. This reuse of the MSB of the first character is appropriate for the intended use case of sending text messages via Iridium SMS, which transmits 8-bit characters. For traditional SMS carriage, one additional byte would be necessary.
The source code for the stats3 program can be found at https://github.com/servalproject/smac and is distributed under the GNU General Public License v2.
5. Results & Conclusions
Table 6 presents a summary of the performance of the stats3 scheme described above against the various corpora and example messages associated with the existing short message compression schemes, and compares this with the performance of the other schemes where data are available or could be produced. The stats3 statistics were generated by processing 203,661 messages of the private Twitter corpus. The remaining 145,333 messages were used for the actual test, for both stats3 and SMAZ to provide comparability. Table 7 compares the speed of stats3 with SMAZ on the private Twitter corpus.
It is clear that stats3 is much slower than SMAZ, but that in return, stats3 easily outperforms both TS03.42 and SMAZ on all inputs. Nonetheless, stats3 is still able to process tens of thousands of messages per second on a single modern CPU, and is more than fast enough to run on a mobile telephone handset or similar embedded device connected to a satellite SMS module. The memory use of stats3 is less than 2 MB, including the statistical model and dictionary. While larger than the approximately 10 KB required for SMAZ, it remains small

Table 6. Compressed message sizes as a percentage of uncompressed size (lower numbers are better).

Table 7. Speed comparison of SMAZ and stats3 (Mac Book Pro, OSX 10.7.3, 2.7 GHz Intel Core i7, 16 GB 1333 MHz DDR3).
enough to be comfortably included in a smart-phone or smart-phone application.
The difference in compression performance between SMAZ and stats3 for the more SMS and Twitter-like messages is particularly striking, providing evidence for what is already intuitively apparent, i.e., that SMS and Twitter messages differ substantially in composition from normal language. This also suggests that TS03.42 requires substantial revision if it is to remain relevant in the light of realistic message composition.
Focusing on the two largest SMS corpora as being the most likely to be predictive of the performance of stats3 on SMS messages in the general case, stats3 achieved a message-weighted average compressed message length of just 43.9% of uncompressed message length, outperforming all short message compression schemes surveyed in this paper. For more “English like” language, such as the GSM sample message 1 and the Pie Floater text, performance is even better, around 40% of uncompressed message size. Thus we suggest that through stats3, the state of the art in short message compression has been advanced, particularly for the compression of SMS and Twitter messages.
6. Future Work
There are several areas that offer potential for improving the performance of the stats3 scheme. First, encoding of rare and non-textual characters, including unicode characters has been left all but unexplored. Second, higher order statistical modeling of the case of letters in words is likely to result in some improvements there. However, the area where the most yield is expected is on improving the mono-case textual character encoder, which typically accounts for 90% of the length of a compressed message. Using fixed-order statistics is suboptimal here, because it introduces relatively high data storage requirements (approximately 1.5 MB for 3rd order statistics for a 69- character alphabet), especially for mobile devices, even though most of those statistics will be zero. A better approach is to replace the fixed-order model with a variable-order model that models more deeply where it is warranted, and less deeply otherwise. This has the potential to do away with the need for a separate word list altogether, which both simplifies and potentially improves the compression and speed performance of the system. Finally, the variable-order statistical model should be loadable from a binary file format, rather than be an irreplacable part of the program, so that the model can be updated as desired in applications where that would be useful.
REFERENCES
- P. Gardner-Stephen, “The Serval Project: Practical Wireless Ad-Hoc Mobile Telecommunications,” 2011. http://developer.servalproject.org/files/CWN_Chapter_Serval.pdf
- P. Gardner-Stephen and R. Challans and A. Bettison and J. Lakeman and C. Wallis, “The Serval Project,” 2012. http://servalproject.org
- P. Gardner-Stephen and J. Lakeman and R. Challans and C. Wallis and A. Stulman and Y. Haddad, “MeshMS: Ad Hoc Data Transfer within Mesh Network,” International Journal of Communications, Network and System Sciences, Vol. 5, No. 8, 2012, pp. 496-504. http://dx.doi.org/10.4236/ijcns.2012.58060
- P. Gardner-Stephen and S. Palaniswamy, “Serval Mesh Software-WiFi Multi Model Management. Proceedings of the 1st International Conference on Wireless Technologies for Humanitarian Relief in ACWR 11, New York, 2011, pp. 71-77. http://dx.doi.org/10.1145/2185216.2185245
- European Telecommunications Standards Institute, “Digital Cellular Telecommunications System (Phase 2+); Compression Algorithm for Text Messaging Services (GSM TS 03.42 Version 7.1.1 Release 1998),” 1999.
- European Telecommunications Standards Institute, “Digital Cellular Telecommunications System (Phase 2+); Universal Mobile Telecommunications System (UMTS); LTE; Compression Algorithm for Text Messaging Services (3GPP TS 23.042 version 11.0.0 Release 11),” 2012.
- P. G. Howard and J. S. Vitter, “Arithmetic Coding for Data Compression,” Proceedings of IEEE, Vol. 82, No. 6, 1994, pp. 857-865. http://dx.doi.org/10.1109/5.286189
- P. G. Howard and J. S. Vitter, “Analysis of Arithmetic Coding for Data Compression,” Information Processing and Management, Vol. 28, No. 6, 1992, pp. 749-764. http://dx.doi.org/10.1016/0306-4573(92)90066-9
- G. G. Langdon Jr., “An Introduction to Arithmetic Coding,” IBM Journal of Research and Development, Vol. 28, No. 2, 1984, p. 135. http://dx.doi.org/10.1147/rd.282.0135
- J. Rissanen and G. G. Langdon, “Arithmetic Coding,” IBM Journal of Research and Development, Vol. 23, No. 2, 1979, pp. 149-162. http://dx.doi.org/10.1147/rd.232.0149
- A. Sanko, “Five Cents on Arithmetic Coding,” Technical Report, 2005. http://www.codeguru.com
- I. H. Witten and Radford M. Neal and J. G. Cleary. “Arithmetic Coding for Data Compression,” Communications of the ACM, Vol. 30, No. 6, 1987, pp. 520-540. http://dx.doi.org/10.1145/214762.214771
- CleverTexting, myMobile Ergonomics. http://clevertexting.com
- SMSzipper, Acticom GmbH. http://smszipper.com
- Panini Keypad, Luna Ergonomics Private Ltd. http://www.paninikeypad.com
- T. M. Mahmoud and B. A. Abdel-latef and A. A. Ahmed and A. M. Mahfouz and T. M. Mahmoud and B. A. Abdel-latef and A. A. Ahmed and A. M. Mahfouz, “Hybrid Compression Encryption Technique for Securing SMS,” International Journal of Computer Science and Security, 2009.
- J. L. Gailly, “Gzip Program and Documentation,” 1993.
- M. Burrows and D. J. Wheeler, “A Block-Sorting Lossless Data Compression Algorithm,” Technical Report, 124, Digital Equipment Corporation, 1994.
- J. Seward, M. Burrows, D. Wheeler, P. Fenwick and A. Moffat and Radford Neal and Ian Witten, “The BZIP2 Compression Program,” 2001.
- M. V. Mahoney, “Adaptive Weighing of Context Models for Lossless Data Compression,” Technical Report, CS-2005-16, Florida Institute of Technology CS Department, 2005.
- T. J. Ferguson and J. H. Rabinowitz. Self-Synchronizing Huffman Codes. IEEE Transactions on Information Theory, Vol. 30, No. 4, 1984, p. 687. http://dx.doi.org/10.1109/TIT.1984.1056931
- R. G. Gallager, “Variations on a Theme by Huffman,” IEEE Transactions on Information Theory, Vol. IT-24, No. 6, 1978, pp. 668-674.
- D. A. Huffman, “A method for the construction of minimum redundancy codes,” Proceedings of the IRE, Vol. 40, 1952, pp. 1098-1101. http://dx.doi.org/10.1109/JRPROC.1952.273898
- M. Jakobsson, “Huffman Coding in Bit-Vector Compression,” Information Processing Letters, Vol. 7, No. 6, 1978, pp. 304-307. http://dx.doi.org/10.1016/0020-0190(78)90023-6
- J. van Leeuwen. “On the Construction of Huffman Trees. Proceedings of 3rd International Colloqium on Automata, Languages and Programming, 1976, pp. 382-410.
- Salvatore Sanfilippo, “SMAZ—Compression for Very Small Strings,” 2009. https://github.com/antirez/smaz
- T. A. Almeida, J. M. G. Hidalgo and A. Yamakami, “Contributions to the Study of SMS Spam Filtering: New Collection and Results,” Proceedings of the 11th ACM Symposium on Document Engineering in DocEng‘11, New York, 2011, pp. 259-262. http://dx.doi.org/10.1145/2034691.2034742
- M. T. Nuruzzaman, L. Changmoo and C. Deokjai, “Independent and Personal SMS Spam Filtering,” 2011 IEEE 11th International Conference on Computer and Information Technology (CIT), 2011, pp. 429-435.
- R. McCreadie, I. Soboroff, J. Lin, C. Macdonald, I. Ounis, and D. McCullough, “On Building a Reusable Twitter Corpus,” Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval in SIGIR ‘12, New York, 2012, pp 1113-1114. http://dx.doi.org/10.1145/2348283.2348495
- C. Constantinescu, J. Q. Trelewicz and R. B. Arps, “Natural Language Insensitive Short Textual String Compression,” 2004, pp. 1-10.
- A. Moffat and L. Stuiver, “Binary Interpolative Coding for Effective Index Compression,” Information Retrieval, Vol. 3, No. 1, 2000, pp. 25-47. http://dx.doi.org/10.1023/A:1013002601898
NOTES
1http://dev.twitter.com/docs/streaming-apis/streams/public; on-line; accessed 15 November 2012.

