Engineering
Vol.6 No.9(2014), Article
ID:48513,9
pages
DOI:10.4236/eng.2014.69053
High Effective FE Simulation Methods for Deformation and Residual Stress by Butt Welding of Thin Steel Plates
Mikihito Hirohata, Yoshito Itoh
Graduate School of Engineering, Nagoya University, Nagoya, Japan
Email: hirohata@civil.nagoya-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 June 2014; revised 18 July 2014; accepted 28 July 2014
ABSTRACT
In order to propose high effective simulation using finite element method (FEM) for predicting deformation and residual stress generated by one pass butt welding, a series of numerical analyses were carried out. By idealizing the movement of heat source (the instantaneous heat input method), the tendency of welding out-of-plane deformation and the residual stress distribution could be predicted. The computing time was around 9% of that by the precise model with considering the movement of heat source. On the other hand, applicability of two dimensional shell elements instead of generally used three dimensional solid elements was examined. The heat input model with considering the temperature distribution in the thickness direction was proposed for the simulation by using the shell elements. It was confirmed that the welding out-of-plane deformation and residual stress could be predicted with high accuracy by the model with shell elements and the distributed heat input methods. The computing time was around 8% of that by the precise model with solid elements.
Keywords:Welding Deformation, Residual Stress, Butt Welding, FEM, Shell Element

1. Introduction
In constructing steel structures, welding is generally used for joining and assembling members. Then, welding deformation and residual stress are inevitably generated due to expansion and shrinkage of welded parts caused by local heating/cooling. Welding deformation and residual stress influence the accuracy of manufacturing, load carrying capacity and fatigue strength of members [1] . In the case that the welding deformation becomes larger than the acceptable limit, it is required to be straightened. On the other hand, high residual stress should be released by annealing in the welded joints of important parts of structures. A high cost and a long time will be necessary due to these processes. Therefore, it is important that welding deformation and residual stress are predicted and controlled.
For predicting welding deformation and residual stress generated in structural steel members, numerical simulation by thermal elasto-plastic analysis based on FEM is an effective method [2] . Welding is a complicated phenomenon involving non-steady heat transfer by movement of heat source, temperature dependency of physical constants and mechanical properties of material and three dimensional elasto-plastic problems [3] . Therefore, it takes huge computing times for welding simulation of large steel structures even though the performance of computer currently becomes faster and faster.
In this study, two calculation methods are examined by which the simulation of welding deformation and residual stress becomes more effective. One is to idealize the movement of heat source which requires many calculation steps and the other is to apply the two dimensional elements instead of three dimensional elements which enlarge the numbers of the nodes and elements of models.
A butt welding of thin steel plates [4] is simulated by these methods. The analytical results by these methods are compared with analytical results modelled precisely. The effectiveness of these methods is examined from the viewpoints of an accuracy of analytical results and computing time. Furthermore, the possibility of application of these methods on simulation for welding deformation and residual stress are investigated.
2. Deformation and Residual Stress Generated by One Pass Butt Welding
2.1. Precise Analysis Model
An analysis model in this study is one pass butt welding of thin steel plates. Figure 1 shows the shapes and dimensions of the model. Kim et al. performed welding experiment for this model [4] . The base metal and the weld metal are SM400A and YGW11 specified by JIS. They are a general structural carbon steel and a corresponding welding wire. The mechanical properties and physical constants with temperature dependencies are shown in the reference [5] . This welding experiment is simulated by thermal elasto-plastic analysis by FEM. Figure 2 shows the precise FE analysis model. A commercial FE program, ABAQUS Ver. 6.10 is used. A half model is adopted by considering symmetric conditions along the weld line. The temperature dependencies of the mechanical properties and physical constants are considered in the analysis. In order to simulate the experiment with high accuracy, three dimensional 8-nodes solid elements are used for modeling the shape of the weld groove. And then, for modeling the movement of weld heat source, heat input elements are generated step by step in the calculation considering the welding speed. In this model, there are 30 elements in the welding direction. The length of each heat input element:  is 10 mm. Therefore, the number of the calculation steps for heat input is 30. And also, additional calculation step for cooling is required after the heating steps. Of course, each calculation step is divided into many fine time increments.
is 10 mm. Therefore, the number of the calculation steps for heat input is 30. And also, additional calculation step for cooling is required after the heating steps. Of course, each calculation step is divided into many fine time increments.
The heat input of welding,  (J/mm) is calculated by Equation (1) [6] . The heat energy,
(J/mm) is calculated by Equation (1) [6] . The heat energy,  (J/mm3) by
(J/mm3) by

Figure 1. One pass butt welding model.

Figure 2. FE analysis model by 8-nodes solid elements.
Equation (2) is given into the heat input elements as a body heat flux. The heating time per each heat input element is decided by dividing the length of each heat input element,  (mm) by the welding speed,
(mm) by the welding speed,  (mm/s).
(mm/s).
A heat transfer from the surface of model is considered as thermal boundary conditions. A rigid body displacement is fixed as mechanical boundary conditions.
 (1)
(1)
 (2)
(2)
Here, : Heat input (J/mm),
: Heat input (J/mm),
 : Heat efficiency (65% to 80% in arc welding [6] ),
: Heat efficiency (65% to 80% in arc welding [6] ),
 : Welding voltage (V),
: Welding voltage (V),
 : Welding current (A),
: Welding current (A),
 : Welding speed (mm/s),
: Welding speed (mm/s),
 : The sectional area of the heat input elements,
: The sectional area of the heat input elements,
 : Heat energy (J/mm3), and
: Heat energy (J/mm3), and
 : The length of each heat input element (mm).
: The length of each heat input element (mm).
2.2. Analysis Results
2.2.1. Temperature Histories
Non-steady thermal conduction analysis was carried out for the butt welding model. Figure 3 shows the temperature histories in the welding. The symbols in the figure represent the experimental results [4] . Measured positions of the temperature were at the bottom of the plates of the center in the welding direction. The distances from the weld line were 15 mm, 30 mm, 50 mm and 80 mm ( , 30, 50 and 80). In order to simulate the temperature histories obtained by the experiment as accurate as possible, the calculations were tried in some times with varying the heat efficiency,
, 30, 50 and 80). In order to simulate the temperature histories obtained by the experiment as accurate as possible, the calculations were tried in some times with varying the heat efficiency, . The analytical results almost agreed with the experimental results when the heat efficiency,
. The analytical results almost agreed with the experimental results when the heat efficiency,  was 0.65.
was 0.65.
In the thermal elasto-plastic analysis, the temperature data obtained by the non-steady thermal conduction analysis is used as input data for the thermal elasto-plastic stress analysis. Therefore, it is indispensable that the temperature data are simulated with high accuracy.
2.2.2. Welding Deformation and Residual Stress
By using the obtained thermal conduction analysis results, thermal elasto-plastic stress analysis was carried out. Figure 4 shows the welding out-of-plane deformation and the distributions of welding residual stress at the cross section of the center in the welding direction . The symbols in the figures represent the experimental results [4] . The residual stress components were obtained by a stress relaxation method. The values of the stress are the average in the thickness direction. The analytical results simulated the experimental results well.
. The symbols in the figures represent the experimental results [4] . The residual stress components were obtained by a stress relaxation method. The values of the stress are the average in the thickness direction. The analytical results simulated the experimental results well.
2.2.3. Computing Time
The results indicated that the welding deformation and residual stress could be simulated with high accuracy by the precisely modeled analysis in which the movement of heat source was considered and three dimensional solid elements were used. When using a general personal computer (CPU 2.93 GHz), the computing time of this

Figure 3. Temperature histories by precise analysis model.
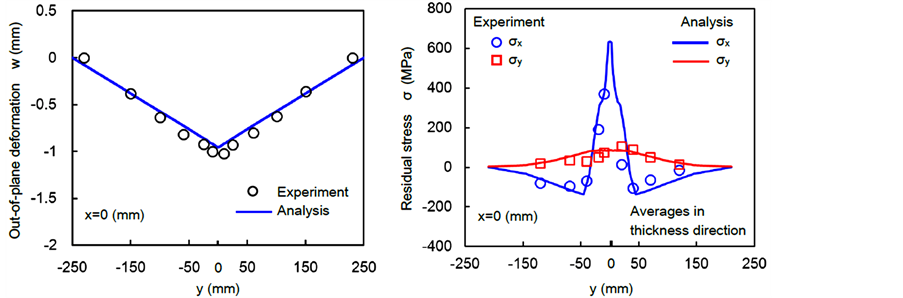
Figure 4. Results of precise analysis model. (a) Out-of-plane deformation; (b) Residual stress.
model was 4416 seconds (around 74 minutes).
3. Idealization for Movement of Heat Source
3.1. Instantaneous Heat Source Model
As shown in Chapter 2, many calculation steps are required for considering the movement of heat source in welding. The longer the weld line becomes, the more calculation steps are necessary. Therefore, it is examined to idealize the movement of heart source in welding. That is, the total heat energy of welding is given into the weld line at one time. This method is well known as instantaneous heat source model [7] . Here, the instantaneous heat source method is applied on the butt welding model (namely, the instantaneous heat source model). The accuracy of analysis model and the computing time are compared with the results by the precise analysis model, that is, the moving heat source model.
In the case of instantaneous heat source model, the heat energy,  (J/mm3) by Equation (3) is given into the all heat input elements in one second. The calculation step for heat input is only one time. And also, making the complicated analysis modeling becomes relatively simple and easy.
(J/mm3) by Equation (3) is given into the all heat input elements in one second. The calculation step for heat input is only one time. And also, making the complicated analysis modeling becomes relatively simple and easy.
 (3)
(3)
3.2. Analysis Results
3.2.1. Temperature Histories
Figure 5(a) shows the temperature histories. In the case of the instantaneous heat source model, the temperature
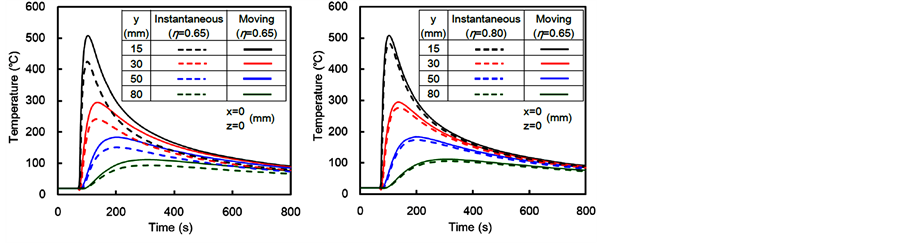
Figure 5. Temperature histories obtained by instantaneous heat source model. (a) Heat efficiency ; (b) Heat efficiency
; (b) Heat efficiency .
.
rose rapidly just after the heat input. On the other hand, the temperature at the center of the weld line rose just after the heat source passes that section in the case of the moving heat source model. For comparing with the moving heat source model, the welding start time of the instantaneous heat source model was shifted.
Even though the total heat energy was the same, the maximum temperature of the instantaneous heat source model was lower than that of the moving heat source model. This was because the temperature of the instantaneous heat source model rose in the short time and decreased after that. On the other hand, the temperature of the moving heat source model gradually rose with the passage of the heart source during the relatively long time.
In order to simulate the temperature histories by the instantaneous heat source model as close to those by the moving heat source model as possible, the heat efficiency,  was changed from 65% to 80%. Figure 5(b) shows the temperature histories in the case that the heat efficiency,
was changed from 65% to 80%. Figure 5(b) shows the temperature histories in the case that the heat efficiency,  was 80%. The maximum temperature of the instantaneous heat source model was almost agreed with that of the moving heat source model.
was 80%. The maximum temperature of the instantaneous heat source model was almost agreed with that of the moving heat source model.
3.2.2. Welding Deformation and Residual Stress
By using the temperature data in the case that the heat efficiency,  was 80%, the thermal elasto-plastic analysis was carried out. Figure 6 shows the welding out-of-plane deformation and the distributions of welding residual stress at the cross section of the center in the welding direction
was 80%, the thermal elasto-plastic analysis was carried out. Figure 6 shows the welding out-of-plane deformation and the distributions of welding residual stress at the cross section of the center in the welding direction . Even though the magnitude of the welding out-of-plane deformation of the instantaneous heat source model was smaller than that of the moving heat source model, their tendencies were the same. The magnitude of the out-of-plane deformation of the instantaneous heat source model was around 72% of that of the moving heat source model. On the other hand, the residual stress distributions of both models were agreed with each other.
. Even though the magnitude of the welding out-of-plane deformation of the instantaneous heat source model was smaller than that of the moving heat source model, their tendencies were the same. The magnitude of the out-of-plane deformation of the instantaneous heat source model was around 72% of that of the moving heat source model. On the other hand, the residual stress distributions of both models were agreed with each other.
In order to investigate the reason why the magnitude of welding out-of-plane deformation of the instantaneous heat source model was smaller than that of the moving heat source model, the generation histories of the welding out-of-plane deformation of both models are shown in Figure 7.
In the case of the moving heat source model, the out-of-plane deformation at the center of the weld line occurred when the heat source passed that section (the time was 30 s). Because of the V-shaped groove, the heat input at the upper side was larger than that at the lower side in the thickness direction. Therefore, the shrinkage in the direction perpendicular to the weld line was larger at the upper side rather than at the lower side. As a result, V-shaped out-of-plane deformation occurred [6] . On the other hand, in the case of the instantaneous heat source model, the large expansion in the direction perpendicular to the weld line occurred when the heat input started. Because the heat input at the upper side was larger than that at the lower side in the thickness direction due to the V-shaped groove, the expansion at the upper side was larger than that at the lower side. Therefore, the inverted V-shaped out-of-plane deformation occurred firstly. After that, the expanded material shrunk and the V-shaped out-of-plane deformation was generated in the cooling process. As a result, the finally generated outof-plane deformation of the instantaneous heat source model became smaller than that of the moving heat source model.
3.2.3. Applicability of Instantaneous Heat Source Model
The computing time of the instantaneous heat source model was 387 seconds (around 6.5 minutes). It was around 9% of that of the moving heat source model.
The generation mechanism of the out-of-plane-deformation of the instantaneous heat source model differed

Figure 6. Welding out-of-plane deformation and residual stress by instantaneous model. (a) Welding out-of-plane deformation; (b) Welding residual stress.

Figure 7. Generation histories of welding out-of-plane deformation.
from that of the moving heat source model. However, the tendency of the out-of-plane deformation could be predicted by the instantaneous heat source model even if the prediction accuracy of magnitude of out-of-plane deformation was not required so high. Furthermore, the welding residual stress distribution could be accurately predicted by the instantaneous heat source model. When the required accuracy of welding out-of-plane deformation is not so high or when only the prediction of residual stress distribution is required, the instantaneous heat source model will be sufficiently available.
4. Application of Two Dimensional Shell Elements
4.1. Shell Model
One of the reasons why the numerical simulation of welding by FEM takes a huge computing time is the use of three dimensional solid elements. For modeling the groove shape, solid elements should be used and some layers should be made in the thickness direction even though the thickness of the plate is thin. Therefore, the numbers of nodes and elements becomes large.
Here, application of two dimensional shell elements on the welding simulation is examined. By using the shell elements, the number of nodes and elements in the thickness direction can be decreased. Figure 8(b) shows the image of the analysis model using 4-nodes shell elements (namely, the shell model). In the case of the precise analysis model using 8-nodes solid elements (namely, the solid model), the shape of groove can be simulated. Even though the shape of groove cannot be considered in the shell model, the sectional area of heat input element is made to be the same as that of the solid model. And then, heat energy calculated by Equation (4) is given into the heat input elements as concentrated heat flux. For calculating the heat energy, the heat efficiency,  of 0.65 is used as well as the case of the solid model. The movement of heat source is considered in both the solid model and the shell model.
of 0.65 is used as well as the case of the solid model. The movement of heat source is considered in both the solid model and the shell model.
 (4)
(4)
Here,  , the number of nodes assembling the heat input elements.
, the number of nodes assembling the heat input elements.
By the way, the out-of-plane deformation occurs due to a difference of temperature between upper and lower surfaces of plates in the case of one pass butt welding of thin steel plates with V-groove [6] . In other words, heat energy at upper surface is larger than that at lower surface. Therefore, larger shrinkage in cooling process of welding occurs at upper surface rather than at lower surface. By the above proposed shell model, the difference of the heat energy between the upper and the lower surfaces is not considered because the heat input into the elements is uniform in the thickness direction. Therefore, the out-of-plane deformation may not occur.
To solve this problem, a heat input method for the shell model shown in Figure 8(c) is also proposed in this study. The linear distribution of the heat energy in the thickness direction calculated by Equation (5) is considered. The difference of the heat energy between the upper and the lower surfaces is determined by the geometry of V-groove shape. The distributed heat energy is given into each integration point in the heat input elements.
 (5)
(5)
Here, : The distributed heat energy (J/mm3),
: The distributed heat energy (J/mm3),
 : The
: The  -coordinate of each integration point,
-coordinate of each integration point,
 : The width of heat input elements, and
: The width of heat input elements, and
 : The number of integration points in the thickness direction.
: The number of integration points in the thickness direction.
4.2. Analysis Results
4.2.1. Temperature Histories
Figure 9 shows the temperature histories in the welding. The maximum temperatures at the position of  of the both shell models with uniform and distributed heat inputs were higher than that of the solid model by around 40 degrees Celsius. The reason of it was possibly the difference of the shapes of the heat input elements. That is to say, the width of the heat input elements at the bottom of the shell model was wider than those of the solid model. Therefore, the larger heat energy reached to the temperature measured points in the shell model
of the both shell models with uniform and distributed heat inputs were higher than that of the solid model by around 40 degrees Celsius. The reason of it was possibly the difference of the shapes of the heat input elements. That is to say, the width of the heat input elements at the bottom of the shell model was wider than those of the solid model. Therefore, the larger heat energy reached to the temperature measured points in the shell model

Figure 8. Image of shell model. (a) Solid model; (b) Shell model with uniform heat input; (c) Shell model with distributed heat input.

Figure 9. Temperature histories obtained by shell models. (a) Results by uniform heat input; (b) Results by distributed heat input.
compared with the solid model.
Figure 10 shows the temperature differences between the upper and the lower surfaces of heat input elements of each model. Even though the temperature differences did not occur in the shell model with uniform heat input, it occurred in the shell model with distributed heat input as well as the solid model.
4.2.2. Welding Deformation and Residual Stress
Figure 11(a) shows the welding out-of-plane deformations at the center of the welding direction. In the case of the shell model with uniform heat input, the out-of-plane deformation scarcely occurred as expected. On the other hand, the out-of-plane deformation by the shell model with distributed heat input almost agreed with that by the solid model. The difference of magnitude of the out-of-plane deformation between the shell and the solid models was around 7%.
Figure 11(b) shows the distributions of welding residual stress at the cross section of the center in the welding direction. Both of the analytical results by the solid model and by the shell models with uniform and distributed heat inputs were almost the same with each other.
By considering the distribution of the heat energy in the thickness direction in the shell model, the welding out-of-plane deformation could be simulated with high accuracy. It could be said that the proposed heat input

Figure 10. Temperature differences between upper and lower surfaces.

Figure 11. Welding out-of-plane deformation and residual stress by shell models. (a) Welding out-of-plane deformation; (b) Welding residual stress.
method was valid. By the way, the computing time of the shell model with uniform heat input was 342 seconds (5.7 minutes). That with distributed heat input was 368 seconds (around 6.1 minutes). The computing times of the shell models were around 8% of that of the solid model.
5. Conclusions
In order to propose the effective calculation methods by FEM for predicting deformation and residual stress generated by one pass butt welding of thin steel plates, a series of numerical analyses were carried out.
The obtained main results are as follows.
The effect of idealizing the movement of heat source in welding (the instantaneous heat input model) was examined. It was confirmed that the generation mechanism of welding out-of-plane deformation by the instantaneous heat input model differed from that by the precise model considering the movement of heat source.
Even though the tendency of out-of-plane deformation could be predicted, the magnitude of out-of-plane deformation of the instantaneous heat source model was around 72% of that of the moving heat source model. On the other hand, the residual stress distribution of the instantaneous heat source model was almost the same as that of the moving heat source model.
The computing time by the instantaneous heat source model was around 9% of that of the moving heat source model. When the required accuracy of welding out-of-plane deformation is not so high or when only the prediction of residual stress distribution is required, the instantaneous heat source model will be sufficiently available.
Applicability of two dimensional shell elements instead of generally used three dimensional solid elements was examined. When the temperature distribution in the thickness direction was not considered, the welding outof-plane deformation could not be simulated well. Therefore, the heat input method with considering the temperature distribution in the thickness direction was proposed for the simulation by using the shell elements.
It was confirmed that the welding out-of-plane deformation and residual stress could be predicted with high accuracy by the model with shell elements and the distributed heat input method. The difference of magnitude of the out-of-plane deformation between the shell model and the solid model was around 7%.
The computing time by the shell model was around 8% of that by the solid model.
The obvious effectiveness could be confirmed even in the simple analysis model in this study. The results indicated that the larger analysis models such as actual steel structures are simulated, the higher effectiveness by using the proposed simulation methods will be expected.
Acknowledgements
This research was partly supported by the Sasakawa Scientific Research Grant from the Japan Science Society.
References
- Japan Society of Civil Engineers (2005) Guidelines for Stability Design of Steel Structures. MARUZEN Co., Ltd., Tokyo.
- Lindgren, L.-E. (2006) Numerical Modelling of Welding. Computer Methods in Applied Mechanics and Engineering, 195, 6710-6736. http://dx.doi.org/10.1016/j.cma.2005.08.018
- Zhu, X.K. and Chao, Y.J. (2002) Effects of Temperature Dependent Material Properties on Welding Simulation. Computers and Structures, 80, 967-976. http://dx.doi.org/10.1016/S0045-7949(02)00040-8
- Kim, Y.-C., Lee, J.-Y., Sawada, M. and Inose, K. (2007) Verification of Validity and Generality of Dominant Factors in High Accurate Prediction of Welding Deformation. Quarterly Journal of Japan Welding Society, 25, 450-454.
- Kim, Y.-C., Lee, J.-Y. and Inose, K. (2007) Dominant Factors for High Accurate Prediction of Distortion and Residual Stress Generated by Fillet Welding. International Journal of Steel Structures, 7, 93-100.
- Japan Welding Society (2003) A Handbook of Welding and Joining. 2nd Edition, MARUZEN Co., Ltd., Tokyo.
- Satoh, K. (1967) On Heat Conduction by Moving Heat Source. Journal of the Japan Welding Society, 36, 154-159.

