American Journal of Analytical Chemistry
Vol.05 No.07(2014), Article ID:45971,8 pages
10.4236/ajac.2014.57050
Preliminary Application of Combinatorial Measurement and Regression Analysis Method to High Precision Instrumental Analysis
Hongyi Zheng
Department of Chemistry, China West Normal University, Nanchong, China
Email: Zheng-HYtom@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 April 2014; revised 9 May 2014; accepted 16 May 2014
ABSTRACT
Using the determination of micro-Fe by 1,10-phenanthroline spectrophotometry as an example, this paper systematically introduces the methodic principle, operation step, and data processing of the combinatorial measurement and regression analysis method application in the instrumental analysis, which include: calibration curve best linear equation is set up, measurand best linear equation is set up, and calculation of best value of a concentration. The results show the means of thrice determination , s = 0 μg/mL, RSD = 0. Results of preliminary application are simply introduced in the basic instrumental analysis for atomic absorption spectrophotometry, ion-selective electrodes, coulometry and polarographic analysis; at the same time, the results are contrasted to results of normal measurement.
, s = 0 μg/mL, RSD = 0. Results of preliminary application are simply introduced in the basic instrumental analysis for atomic absorption spectrophotometry, ion-selective electrodes, coulometry and polarographic analysis; at the same time, the results are contrasted to results of normal measurement.
Keywords:
combinatorial measurement and regression Analysis Method, instrumental Analysis, High precision, Application

1. Introduction
The combinatorial measurement and regression analysis method is a new high precision method of measurement in analytical chemistry. It organically combines the principle of combinatorial measurement in metrology with the regression analysis method in mathematical statistics. At measuring instrument of an accuracy class under the condition that is subjected to certain limit, it can raise the accuracy of measurement and achieve a zero deviation measurement with the value of a quantity of its determination result at diagraphs of 1,000,000 cents number(titration analysis) and 100,000 cents number (instrumental analysis). Its type of measurement and data processing method, widespread be applicable to titration analysis and each kind of instrumental analysis realm, embodied the total and core of various analysis technique method thus.
Relevant combinatorial measurement of metrology principle [1] , the combinatorial measurement and the regression analysis method allied use of principle. The combinatorial measurement and regression analysis methods are applied to the standardization for standard volumetric solution concentration [2] [3] , and at preliminary application of high precision titrimetry etc. research aspects [4] , have already had information. At the same time, in the aspects of the evaluation of uncertainty for determination result, the methods have related information [5] -[8] . In the contemporary, the instrumental analysis has already become the main current of analytical chemistry [9] , is a modern analysis chemistry to apply the most extensive method and technique in each profession of national economy, each sector and in each realm of science technique [10] , therefore, further inquire into application study for the combinatorial measurement and regression analysis method in the instrumental analysis, have more important actual meaning.
From the angle of metrology, the measurement method of analytical chemistry belongs to an indirect measurement way. Each kind of instrumental analysis method usually is to adopt a calibration curve method to come to quantitative, to each measurement points data according to linear regression analysis carry on calculation. But, generally speaking, the value of regression analysis isn’t the best value of a quantity and there are still some errors of measurement. These error sources mainly have: the methodical error aroused by the blemish of common measurement principle―common measurement just combinatorial measurement of an especially example, it can not adopt the principle of method of least square to carry on variance of the mean in order to make parts of systematic error randomization, offset thus it; carry on one-variable linear regression analysis to compute to the common measured data once produce of calculation error; and because of instrumental precision the instrumental error aroused by not enough highly.
Using the determination of micro-Fe by 1,10-phenanthroline spectrophotometry as an example, this paper systematically introduces the combinatorial measurement and regression analysis method application about methodic principle, operation step and data processing in the instrumental analysis, including: calibration curve best linear equation is set up, measurand best linear equation is set up, and calculation of best value of a concentration. Results of preliminary application are simply introduced in the basal instrumental analysis for atomic absorption spectrophotometry, ion-selective electrodes, coulometry and polarographic analysis; at the same time, the results are contrasted to results of normal measurement.
2. Material and Experiment
2.1. Instruments and Reagents
Visible spectrophotometer (723 A type, precise scientific instrument limited company in Shanghai).
NH4Fe(SO4)2・12H2O (Ammonium iron(Ⅲ) sulfate); 1,10-phenanthrolinemonohydrate (1.5 g/L; hydroxylamine hydrochloride (100 g/L; sodium acetate (1 mol/L); hydrochloride acid (6 mol/L). Use of reagents is analytically pure.
2.2. Experimental methods
2.2.1. The standard solution ofiron Be Prepared (100.00 μg/mL)
In the combinatorial weighting method, according to the operational program of weighting an specimen [2] , 0.8634 g reagent NH4Fe(SO4)2・12H2O be accurately weighted.
The reagent is placed into a 250 mL beaker in, to join the 20 mL 6 mol/ L HCl solution and a little amount water. It is transferred into the 1000.00 mL graduated flask after being dissolved, use water dilution to engrave one degree line, shake up.
Assume that the actual quality of weighting paper as x1 and the actual quality of reagent as x2, from above- mentioned direct measured value results mi, build up condition equation set: x1 = m1, x2 = m2, x1 + x2 = m3; build up and solve the binary normal equation set for the quality x: 2x1 + x2 = m1 + m3, x1 + 2x2 = m2 + m3. Thus compute the best value for the x2 ( compute to 6 places of decimals).
2.2.2. The standard series Solution of Iron and specimen solution Be prepared
In 6 × 50 mL graduated flasks, use a 1 mL pipette, according to a kind of operational program for the principle of combinatorial measurement [1] [3] , join the above-mentioned the standard solution of iron, constitute the combinatorial series specimen solution of iron: 0.000 mL (reagent blank ), 0.200 mL (serial number 1), 0.400 mL (serial number 2), 0.600 mL (serial number 3), 0.800 mL (serial number 4), 1.000 mL (serial number 5).
In each graduated flask, join the 1 mL hydroxylamine hydrochloride (100 g/L) respectively, shake up; Join 2 mL 1,10-phenanthrolinemonohydrate (1.5 g/L) and the 5 mL sodium acetate solution (1 mol/L) again, shake up; use water dilution to engrave one degree line, shake up; place 10 minutes.
Moreover, accurately quantity to take measured specimen: 4.00 mL, 6.00 mL and 10.00 mL, are constituting a combinatorial series specimen solution, being placed to the 50 mL graduated flask respectively (serial number is 6, 7, 8), join various of reagent according to the step of preparation of the standard solution, use water dilution to engrave one degree line.
2.2.3. Absorbance A Be Measured
Under the working wavelength (λ = 508.0 nm) condition for making selection, measure absorbance Ai (i = 1 - 5) of the combinatorial standard solution of iron; under the same condition, measure absorbance of each combinatorial specimen.
The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire journals, and not as an independent document. Please do not revise any of the current designations.
3. Results and Discussion
First, according to the data processing method of common measure (one-variable linear regression analysis), to the data of combinatorial measurement make the first-time regression analysis, get the linear equation of calibration curve and the content of iron in specimen. table 1 is concerning the measured data record and data processing result.
From the table 1 it is thus clear that, according to the data processing method of common measure, the linear equation of calibration curve gaining isn’t the best straight line (r ≠ 1); and the standard deviation of three times measured results is bigger (s ≠ 0); each regression that absorb intensity of light value although at same straight line up (namely satisfy line sexual behavior), the dissatisfied foot and each standard iron content is opposite should of combination number relation (namely combination measure medium of add with of the relation between relation or multiple). This namely expresses: measure according to the normal regulations of data treatment, each the regression that absorb intensity of light gaining analyzes value not the best value, still exist a certain diagraph error margin. For this, have to adopt to combine a regression analysis method, pass to solve the condition equation and method equation of combining the diagraph, and analyze a method with regression allied use to give a precision to correct.
3.1. Best linear equation of Calibration Curve Is set Up
In the preparing of the series standard solution process, in order to pipette, use water dilution to engrave one degree line and operating the various error that the etc. factor produces, will propagate each the Ai that absorbance of measured value of follow-up, at combination and regression of the process that the cycling data processing, will be lowered into minimum degree gradually. From here, The mass of iron in each serial number specimen of iron standard series is seen to relative small error variable, and assume for the best value, type of combinatorial measurement according to it are respectively: x1 = 20.00 μg, x2 = 40.00 μg, x1 + x2 = 60.00 μg, 2x2 = 80.00 μg, x1 + 2x2 = 100.00 μg.
According to the combinatorial relation between the standard solution, suppose the physically best value of each absorbance (relative big error variable) is a yi (i = 1 - 5), can be built up as follows a condition equation set is according to the direct measured value result:

Table 1. common first regression analysis.
Build up and solve the binary normal equation set for the absorbance yi:
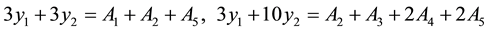
The best value (compute to 6 places of decimals) that computes y1, y2 and it each combination value (y1+ y2, 2y2, y1 +2y2) from here.
Supposing each the regression value 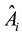 that absorbance in table 1 is Ai, the generation goes into the last type to carry on the combination computes for the first time, the physically best value that can get each absorbance of standard solution and its combination; again with the best value of absorbance y to the mass of iron of standard solution of the best value x make the regression analysis a calculation for the second time; …; end with regression value
that absorbance in table 1 is Ai, the generation goes into the last type to carry on the combination computes for the first time, the physically best value that can get each absorbance of standard solution and its combination; again with the best value of absorbance y to the mass of iron of standard solution of the best value x make the regression analysis a calculation for the second time; …; end with regression value  of the regression analysis for the sixth time make the combination computes for the sixth time, with yi and its the combination value make the regression analysis a calculation for the seventh time to the mass of iron of standard solution of the best value x, each combination and regression calculation of comprehensive result is table 2.
of the regression analysis for the sixth time make the combination computes for the sixth time, with yi and its the combination value make the regression analysis a calculation for the seventh time to the mass of iron of standard solution of the best value x, each combination and regression calculation of comprehensive result is table 2.
From the table 2 it is thus clear that, the combinatorial measurement and regression analysis method pass the change type of measurement and replace to circularly compute of regression analysis, the relevant the parameter value of a quantity of regression equation of common measure and made to show calibration and improve: The intercept a declines from about 2% to 1/1,000,000 as a result be tended to zero; gradient b slightly already lower be tended to one constant; the correlation coefficient r equals 1, convert the related relation between variable into the near settled functional relation, then pass to the best value of absorbance y of n time combination and (n + 1) time regression analysis calculation, the best linear equation of calibration curve is set up:
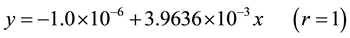
3.2. Best Linear equation of Measured Is Set Up
In the process of measurement of absorbance, measured specimen solution is the measurement type of a combination to join and use water dilution to engrave one degree line. Same truth, the error of measurement of absorbance of specimen as well opposite bigger and can not directly get into to carry on a calculation in the best linear equation of calibration curve. For this, have to carry on to 3 measurement value of absorbance combinatorial measurement and regression analysis of calibration, make the quantity of threes value relation satisfy combinatorial relation and linear relation at the same time. It corrects to is divided into calibration of first step and precision calibration.
3.2.1. Calibration of First step for Value of a Quantity of absorbance of specimen
According to table 3 win the best value of regression analysis of the seventh-time regression equation, respectively to table 1 win three specimen of absorbance Ai to carry on calibration of first step. First compute to correction 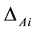 of absorbance error, compute to calibration value of absorbance Ai thus.
of absorbance error, compute to calibration value of absorbance Ai thus.
The 4.00 mL specimen (the 6th): From insert a method to solve:
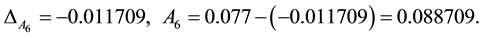 Together the reason can get: 6.00 mL specimen (the 7th) A7 = 0.134008; 10.00 mL specimen (the 8th) A8 = 0.235146.
Together the reason can get: 6.00 mL specimen (the 7th) A7 = 0.134008; 10.00 mL specimen (the 8th) A8 = 0.235146.
Table 2. Calculative results of combinatorial measurement and regression analysis method application (1).
After calibration of first step, each the of quantity value still can not satisfy combinatorial relation and linear relation at the same time and also exist a certain error of measurement, have to adopt to the combinatorial measurement and regression analysis method to carry on a further precision to calibration.
3.2.2. Precision calibration for value of a Quantity of Absorbance of specimen
Suppose calibration value of absorbance of 3 specimen as A1, A2 and A3, their the physically the best value are respectively y1, y2 and y3, according to above-mentioned calibrated results, can be built up as follows a condition equation set:
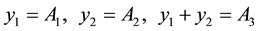
Build up and solve the binary normal equation set of absorbance y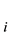 :
:
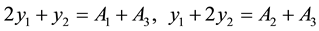
Compute the best value of y1, y2 from here (compute to 6 places of decimals).
Use the A1 (0.088709), A2 (0.134008) A3 (0.235146) make to combination computes for the first time according to the last type and get y1, y2 and y3 With this to the best value of volume of specimen solution x1 = 4.00 mL, x2 = 6.00 mL, x1 + x2= 10.00 mL to make the regression analysis for the first time; …; end makes the com-
Table 3. calculative results of combinatorial measurement and regression analysis method application (2).
bination computes for the fourth time with regression value of the regression analysis for the third time, with yi and its combination value to the best value of volume of specimen solution make the regression analysis a calculation for the fourth time, each combination and regression calculation of comprehensive result is table 3:
From the table 3 it is thus clear that, best linear equation of measurand of absorbance is:
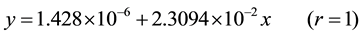
3.3. Calculation of Best value of a Concentration
Be the regression value in best linear equation from combination and regression analysis for the fourth time, namely the best value of measurand of absorbance: 0.092377, 0.138565 and 0.230942, respectively take into best linear equation of calibration curve in Table 3 to carry on a calculation, can get the best value of measurand of mass: x1 = 23.306 μg, x2 = 34.959 μg, x1 + x2 = 58.265 μg; Again respectively be divided by each combinatorial value of measured specimen: 4.00 mL, 6.00 mL, 10.00 mL, Thus compute the best value of measurand of a concentration: ρ1 = 5.8265 μg/mL, ρ2 = 5.8265 μg/mL, ρ3 = 5.8265 μg/mL,  = 5.8265 μg/mL. In consideration of the number of significant figure, ρ1 ≈ 5.83 μg/mL, ρ2 ≈ 5.83 μg/mL, ρ3 ≈ 5.83 μg/mL,
= 5.8265 μg/mL. In consideration of the number of significant figure, ρ1 ≈ 5.83 μg/mL, ρ2 ≈ 5.83 μg/mL, ρ3 ≈ 5.83 μg/mL, 
3.4. The Number of times Problem That the concerning combination and regression Circularly computes
For those according to common measurement principle thus build up of each kind of instrument analysis method, At their data processing process in, general cans do a time one-variable linear regression analysis a calculation, Therefore, their lower the function of error of measurement limited. But, according to the principle of combinatorial measurement from build up of instrumental analysis method, because the combinatorial number relation to of constantly feedback and adjustment, Can make many times one-variable linear regression analysis a calculation, therefore its lower the function of error of measurement obvious. According to its methodical principle, the error of measurement of response of analytical instrument (relative big error variable), be pass to combina-
Table 4. Comparison of results of two methods (1).
tion and regression circularly computes to reduce to gradually minimum, and with the correlation coefficient r = 1 is calculation to stop a point. If experimental error of measurement is big, then circularly compute of number of times is many. Generally speaking, the error of measurement of chemical analysis is opposite smaller, circularly compute of number of times also less (at most 4 - 5 times); the error of measurement of instrumental analysis more big, circulate calculation number of times more (at most can reach to 20 above), for reducing circulating number of times, calibration of first step is necessary and effective. Because circularly computing a work of com- bination and regression is more complicated, In addition to passing general function calculator completion, can also draw up in general calculator procedure software, to the benefit of the actual application and the expansion.
4. At Some Basic instrumental Analysis in of the First step Apply
4.1. Atomic absorption spectrophotometry Determination the Content of the Ca in Tap water
In the normal analysis work of the AAS, generally adopted calibration curve method and standard addition method to practice quantification. With the determination of the content of the Calcium, Magnesium, and Zinc in water specimen and bean milk powder, led to go into metrological principle and method about the combinatorial measurement and regression analysis method, its effect gives satisfaction. Among them, the result of determination of the content of the Ca in the tap water specimen makes the introduction of a synopsis just here. Need to be explanatory BE: the best linear equation of calibration curve is achieved through the combination for the seventh time and regression for the eighth time, the best linear equation of measurand is achieved through the combination for the fifth time and regression for the sixth time. Comparison of results of normal photometric analysis and combinatorial measurement and regression analysis are presented in table 5.
4.2. Ion-Selective electrodes determination the Content of the Fluorine in Water Specimen
In the quantification method of the ISE, calibration curve method is also in common use. Make a brief introduction to the result of determination for the content of the Fluorine in water specimen just here. Need to be explanatory BE: The best linear equation of calibration curve is achieved through the combination for the sixth time and regression for the seventh time, The best linear equation of measurand is achieved through the combination for the fifth time and regression for the sixth time. Comparison of results of normal potential analysis and combinatorial measurement and regression analysis are presented in table 6.
4.3. Coulometry determination the Content of the Vitamin C (Vc)
The quantification method of coulometry, BE according to the Faraday law of one of the strictest laws in the natural science, have the characteristics of high accuracy and high sensitivity.
The methodic error of common coulometry is general and about 0.5%. The precise coulometry that is controlled by the computer then can attain 0.01%. However, if adopt the combinatorial measurement and regression analysis method, it can also make the precise of common coulometry get more significant exaltation. Underneath introductive determination the content of the Vitamin C in the solid specimen is 1. The best linear equation of measurand among them is achieved through combination for the fifth time and regression for the sixth time. Comparison of results of normal coulometry and combinatorial measurement and regression analysis are presented in table 7.
4.4. Polarographic Analysis Determinations the content of the Cadmium in water Specimen
Quantification method of polarographic analysis is generally calibration curve method and standard addition method, twos can adopt to the type of measurement of the combinatorial measurement and regression analysis method to raise its precise further. And, the determination of specimen to the adoption standard addition method, it is similar to apply also. Underneath introductive determination the content of the Cadmium ion in water specimen is 1. The best linear equation of measurand among them is achieved through combination for the sixth time and regression for the sixth time. Comparison of results of normal polarography and combinatorial measurement and regression analysis are presented in table 8.
Table 5. Comparison of results of two methods (2).
Table 6. Comparison of results of two methods (3).
Table 7. Comparison of results of two methods (4).
Table 8. Comparison of results of two methods (5).
5. Conclusion
The combinatorial measurement and regression analysis method commences from the metrological basic of analytical chemistry―error theory and integrates a kind of high precision new method of measurement for building up thus. Because its methodic principle involves the most basal mathematical statistics theory, consequently it has the most extensive actual application prospect. The method not only applies in the high precision measurement at each kind of chemical analysis, but also is applicable to each kind of instrumental analysis methods. Generally speaking, because the error of measurement of instrumental analysis is larger than chemical analysis, so its circulating calculation number of times for the combinatorial measurement and regression analysis is opposite and more, and calculation result of zero deviation measurement point is at 100,000 cents number, which is larger than chemical analysis. The method enriches and develops metrology, the metrological theory and method of measurement of analytical chemistry, make the instrumental analysis method get into precision measurement realm from here.
References
- Lang, C.-Y. (1987) Applied Metrological Detection Error. Metallurgy Industries Press, Beijing, 27-30.
- Zheng, H.-Y., Zhang, J. and Xu, Y. (2011) The Combinatorial Measurement and Regression Analysis Method―Stand- ardization of the Concentration of HCl Standard Volumetric Solutions. Chemistry Bulletin, 74, 170-174.
- Genral Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China (2002) GB/T601-2002. Chemical Reagent Preparations of Standard Volumetric Solutions. Chinese Standard Press, Beijing, 1-24.
- Zheng, H.-Y. (2013) Preliminary Application of Combinatorial Measurement and Regression Analysis Method to High Precision Titrimetry Analysis. Physical Testing and Chemical Analysis, Part B Chemical Analysis, 49, 1097-1102.
- Zheng, H.-Y. (2012) The Combinatorial Measurement and Regression Analysis Method――Quantifying Uncertainty for the Concentration of NaOH Standard Volumetric Solutions. Chemical World, 53, 531-535.
- Chinese National Approbation Laboratory Committee (2002) Quantifying Uncertainty in Analytical Measurement Guide. Chinese Metrology Press, Beijing, 40-49.
- Zheng, H.-Y. (2009) Calculation of Uncertainty in Measurement Caused by End Point Error. Acta Metrologica Sinica, 30, 389-392.
- Zheng, H.-Y. (2010) Calculation of Uncertainty in Measurement Caused by End Point Error in the Redox and Precipitation Titraction. Chinese Journal of Analysis Laboratory, 29, 353-357.
- University of Wuhan (2007) Analytical Chemistry (Version 5) Next Volume. Higher Education Press, Beijing, 2-3.
- Sun, Y.-Q. and Hu, Y.-Z. (2006) Analytical Chemistry (Version 2). Higher Education Press, Beijing, 1.


