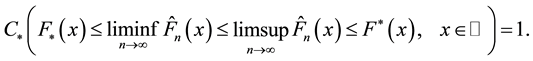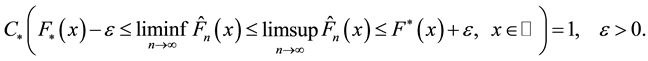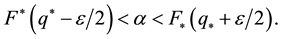Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:55496,2 pages
10.4236/jmf.2015.52010
On Historical Value at Risk under Distribution Uncertainty
Atsushi Iizuka1, Yumiharu Nakano2
1Informatix Inc., Kanagawa, Japan
2Tokyo Institute of Technology, Tokyo, Japan
Email: senkonoshine@yahoo.co.jp, nakano.y.ai@m.titech.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2015; accepted 7 April 2015; published 10 April 2015
ABSTRACT
We investigate the asymptotics of the historical value-at-risk under capacities defined by sublinear expectations. By generalizing Glivenko-Cantelli lemma, we show that the historical value-at- risk eventually lies between the upper and lower value-at-risks quasi surely.
Keywords:
Value-at-Risk, Sublinear Expectation, Capacities, Glivenko-Cantelli Lemma

1. Introduction
In financial industry, the value-at-risk has been one of main tools for risk management (see, e.g., McNeil et al. [1] , and Föllmer and Schied [2] ). In this framework, the random variables for assets or asset returns are assumed to have distributions without uncertainty. In other words, it is implicitly assumed that there are true asset distributions and the estimation difficulty comes from our limited capability. However, it should be remarked that there is a possibility that the assets have the distribution uncertainty, i.e., the assets may have Knightian uncertainty (see Knight [3] ).
To capture the distribution uncertainty, the theory of sublinear expectation is introduced and developed (see Peng [4] [5] and the references therein). In this theory, the term probability is replaced by the ones of the upper and lower capacities induced by the upper and lower expectations, respectively, and the distribution uncertainty is described by the gap between the upper and lower expectations.
In this paper, we consider the value-at-risk type risk measure under the sublinear expectation, where the reference probability measure in the classical framework is replaced by the upper and lower capacities. We call these the upper and lower value-at-risk, respectively. Our aim is to study the asymptotic behavior of the historical value-at-risk under uncertainty. In doing so, we prove a generalization of Glivenko-Cantelli lemma under uncertainty, and then show that the historical value-at-risk eventually lies in between the upper and lower value- at-risks quasi surely.
This paper is organized as follows: In Section 2, we recall the theory of sublinear expectation. Section 3 is devoted to the statement of the main results and its proofs.
2. Sublinear Expectation and Capacities
In this section, we recall the basis of the sublinear expectation, introduced by Peng [4] . Let Ω be a given set and  a linear space of
a linear space of  -valued functions on Ω. We assume that
-valued functions on Ω. We assume that  whenever
whenever 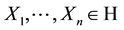 and
and 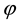 is a bounded function on
is a bounded function on 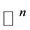 or
or 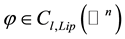 where
where 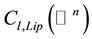 denotes the linear space of functions
denotes the linear space of functions 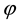 on
on 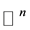 satisfying
satisfying

for some 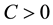 and
and  depending on
depending on . We call an element in
. We call an element in 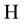 a random variable.
a random variable.
We consider a sublinear expectation , in the sense of [4] . Namely, E is assumed to be satisfy the following conditions: for any
, in the sense of [4] . Namely, E is assumed to be satisfy the following conditions: for any
1) Monotonicity: if 

2) Constant preserving: 

3) Subadditivity:
4) Positive homogeneity: 

Moreover, we assume that 





where 


define capacities, where 1A denotes the indicator function of a set A. That is, each 
1)

2) If 


We refer to Denenberg [6] for the theory of capacities. Throughout this paper, we assume that each 
3) If 


4) If 


Let us recall several concepts in the sublinear expectation theory. The random variable 



We say that 

A sequence 







Then if

3. Main Resutls
For any


Proposition 3.1 Let 

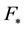

1) 


2)

3) 

Proof. The assertion (1) follows from the monotonicity of 

To prove (2), take 







Similarly, 
Finally, by an argument similar to the proof of (2) with



The proposition above justifies the following definition:
Definition 3.2 For a random variable X, we call the function 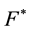

For an IID sequence


If 
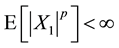


Indeed,
We show a stronger result, which is a generalization of Glivenko-Cantelli lemma.
Theorem 3.3 Let 
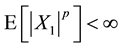
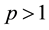

the upper and lower cumulative distribution functions of X respectively, and denote by 

We need the following lemma for the proof of the theorem.
Lemma 3.4 Under the assumtions imposed in Theorem 3.3, for

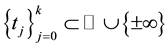
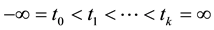
where


Proof. Let




By this recursion, we can find 

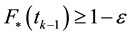

With the help of Lemma 3.4, we can show Theorem 3.3.
Proof of Theorem 3.3. Let 



By (2), we have, 

Thus, 
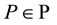



where for
So we have
Now, for any 

so
Therefore, on




If we write 

meaning the assertion of the theorem. □
Recall that for a function 



Then we have the following:
Theorem 3.5 Let 
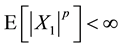
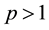




Suppose that for

Then, the historical value-at-risk eventually lies in between the upper and lower value-at-risk, i.e.,
Proof. Consider the event A defined by
In view of Theorem 3.3, it suffices to show that for a given 



To this end, fix 


Thus we can take 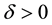
Next, take 
and set
So we have
leading to
References
- McNeil, A. J., Frey, R. and Embrechts, P. (2005) Quantitative Risk Management: Concepts, Techniques and Tools. Princeton University Press, Princeton.
- Föllmer, H. and Schied, A. (2004) Stochastic Finance: An Introduction in Discrete Time. 2nd Edition, Walter de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110212075
- Knight, F.H. (1921) Risk, Uncertainty, and Profit. Houghton Mifflin, Boston.
- Peng, S. (2006) G-Expectation, G-Brownian Motion and Related Stochastic Calculus of Itô’s type, In: Benth, F.E., et al., Eds., Stochastic Analysis and Applications: The Abel Symposium 2005, Springer-Verlag, Berlin, 541-567.
- Peng, S. (2010) Nonlinear Expectations and Stochastic Calculus under Uncertainty. arXiv:1002.4546[math.PR]
- Denneberg, D. (1994) Non-Additive Measure and Integral. Kluwer Academic Publishers, Dordrecht. http://dx.doi.org/10.1007/978-94-017-2434-0
- Chen, Z. (2010) Strong Laws of Large Numbers for Capacities. arXiv:1006.0749[math.PR]