Open Journal of Statistics
Vol.06 No.03(2016), Article ID:67313,8 pages
10.4236/ojs.2016.63035
The Importance of Selection Bias in Internet Surveys
Zerrin Asan Greenacre
Statistic Department, Science Faculty, Anadolu University, Eskisehir, Turkey

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 April 2016; accepted 11 June 2016; published 14 June 2016
ABSTRACT
Nowadays, internet-based surveys are increasingly used for data collection, because their usage is simple and cheap. Also they give fast access to a large group of respondents. There are many factors affecting internet surveys, such as measurement, survey design and sampling selection bias. The sampling has an important place in selection bias in internet survey. In terms of sample selection, the type of access to internet surveys has several limitations. There are internet surveys based on restricted access and on voluntary participation, and these are characterized by their implementation according to the type of survey. It can be used probability and non-probability sampling, both of which may lead to biased estimates. There are different ways to correct for selection biases; poststratification or weighting class adjustments, raking or rim weighting, generalized regression modeling and propensity score adjustments. This paper aims to describe methodological problems about selection bias issues and to give a review in internet surveys. Also the objective of this study is to show the effect of various correction techniques for reducing selection bias.
Keywords:
Internet Surveys, Selection Bias, Weighting Adjustment Procedures

1. Introduction
In the last decades, the internet survey has become a popular tool of data collection. Because internet surveys have several advantages compared to more traditional surveys with personal interviews, telephone interviews, or mail surveys [1] . Internet surveys have some attractive advantages in terms of costs and timeliness:
1) Now that so many people are connected to the Internet. In the world, the number of internet users is 3,366,261,156 people. Also we can see internet users in the world by regions in Figure 1 [2] . The most internet
Figure 1. Internet users in the world by regions November 2015 (source internetworldstats.com).
users are located in Asia and Europe in this figure. The number of internet users in the world is increasing with each passing day. The greater the number of people using the internet, the number of people who responded to the online survey will also increase. An internet survey is a simple means to get access to a large group of potential respondents.
2) Questionnaires can be distributed at very low costs. No interviewers are needed, and there are no mailing and printing costs.
3) Surveys can be launched very quickly. Little time is lost between the moment the questionnaire is ready and the start of the fieldwork. Thus, internet surveys are a fast, cheap and attractive means of collecting large amounts of data. When we search internet survey studies according to years in Figure 2, there is an increase in the number of studies according to years [3] . The data in Figure 2 obtained from web survey methodology web page. Internet surveys were an increase in 2004. The increase in internet research began after 2010. In 2015 and 2016 there was a decrease in the internet survey. Internet studies in Figure 2 cover all types of published work such as articles, presentations.
Internet questionnaires are applied by the interaction of the internet site and the participant, [4] Bethlehem (2008).
Types of Internet Surveys: Internet surveys based on restricted access, and internet surveys based on voluntary participation will be examined [5] .
1) Internet surveys based on restricted access:
E-Mail Surveys: E-mail surveys will be executed on the basis of probability samples which are obtained from a list frame of available e-mail addresses, assuming that is the frame population. There are also relatedcoverage bias issues.
Internet Surveys by E-Mail Invitation: It is also based on a probability sample using the same list frame of available e-mail addresses. Same coverage biases exist for this. For the probability based samples, in addition to the above stated coverage error problems, there will also be nonresponse issues and related adjustments.
2) Internet surveys based on voluntary participation:
Free Access to Internet Surveys: In this case, any respondent can have access to a internet questionnaire on the site, without any restriction.
In terms of population representation, the collected information will have several problems. In this case, the population frame will be undefined, ill defined, or partially defined [6] [7] .
2. The Types of Error in Internet Survey
Surveys estimates will never be exactly equal to the population characteristics they intend to estimate. There is always some error. It has been described possible causes in literature like Kish (1967), Bethlehem (1999). It is shown general survey error in Figure 3 [8] . Total error is divided in two main error as sampling error and
Figure 2. The number of internet surveys according to years (source websm.org).
Figure 3. Classification survey error.
nonsampling error. Nonsampling follows coverage error, nonresponse error and measurement error. These errors should be examined under separate headings.
Internet surveys contain survey error. Although they are very popular nowadays internet survey has several advantages, but this type surveys are also prone to many survey errors. It is useful to evaluate the types of internet surveys currently available in terms of the traditional measures of quality and sources of errors in surveys. While internet surveys generally are significantly less expensive than other modes of data collection, and are quicker to conduct, there are serious concerns raised about errors of non-observation or selection bias. Inference in internet surveys involves three key aspects: sampling, coverage, and nonresponse [9] . Because these are related to selection bias, examination of selection bias has a great importance in internet survey. It is possible to find publications related to selection bias in recent years. It can give some example like [1] [10] [11] . This paper aims to describe methodological problems about selection bias issues and to give a review in internet surveys. Also the objective of this study is to show the effect of various correction techniques for reducing selection bias. It is important to use one correction techniques for reducing selection bias in internet survey used sampling process.
The sampling process for explaining the selection issues are given in the following section.
3. The Types of Sampling in Internet Survey
The key challenge for sampling in internet surveys is that the mode does not have an associated sampling method. For example, telephone surveys are often based on random-digit dialling (RDD) sampling, which generates a sample of telephone numbers without the necessity of a complete frame. On the other hand, similar stra- tegies are not possible for the Web surveys.
While e-mail addresses are relatively fixed (like telephone numbers or street addresses), internet use is a behavior (rather than status) that does not require an e-mail address. Thus, the population of “internet users” is dynamic and is difficult to define. Furthermore, the goal is often to make inference to the full population, not just the Internet users. Table 1 shows alternative sampling methods for internet survey. Here, sampling methods are divided into two parts as non-probability and probability-based according to internet survey type in the above table. The fundamental difference between non-probability sampling and probability sampling is the former lacks random selection-the members of the target population are not being given an equal opportunity to be selected [12] . Some of the main problems of internet surveys are caused by under coverage, nonparticipation and selection.
4. Sampling Selection Issue in Internet Survey
Internet surveys appear in many different forms like in Table 1. There are internet surveys based on probability sampling, for example surveys among students and instructors of a university. Also many internet surveys are not based on probability sampling, for example, surveys conducted by market research organizations. Self-se- lection is the phenomenon that the sample is not selected by means of a probability sample. Instead, it is left to the internet user’s personal participation in a web survey. The survey questionnaire is simply released on the web. Respondents are those people who happen to have internet access, visit the website, and decide to participate in the survey. Participation in a self-selection requires that respondents are aware of the existence of a survey. They have to visit the website accidentally, or they have to follow up a banner or an e-mail message. They also have to decide to fill in the questionnaire on the internet. In this case, the survey researcher is not in control of the selection process [10] [13] . Therefore, estimates of self-selection surveys will be biased.
What difference does it make if a sample consists of self-selected volunteers rather than a probability sample from the target population? The key statistical consequence is bias. Unadjusted means or proportions from non-probability samples are likely to be biased estimates of the corresponding population means or proportions. There are a number of different ways researchers attempt to correct for selection biases, both for probability-based and non-probability online surveys. Weighting adjustment techniques may help to reduce selection bias. Weighting adjustment is based on the use of auxiliary information. Auxiliary information is defined here as a set of variables that have been measured in the survey, and for which the distribution in the population is available. The bias will be large if:
1) The relationship between the target variable and the response behavior is strong;
2) The variation in the response probabilities is large;
3) The average response probability is low.
Table 1. Types of internet surveys samples.
There can be several reasons to carry some kind of weighting adjustment on the response to a web survey: The sample is selected with unequal probability sampling. Nonresponse may cause estimators of population characteristics to be biased. If the target population is wider than the internet population, people without internet can never be selected for the survey. If the sample is selected by means of self-selection, the true selection probabilities are unknown, assuming equal selection probabilities leads to biased estimates. Weighting adjustment techniques may help to reduce a bias [13] .
The weighting techniques described in the following sections can reduce the nonresponse bias provided that, proper auxiliary information is available. The three reasons for weighting described above apply to any survey, whatever the mode of data collection will be. There are two more reasons for weighting that are particularly important for many Web surveys. These reasons are the under-coverage and self-selecting.
5. Approaches to Weighting Adjustment for Sampling Selection Biases
In general there are four weighting methods for adjustments which are given in Table 2 [14] .
Poststratification or weighting class adjustments is an estimation technique that attempts to make the sample representative after the data has been collected. It is the simplest and most commonly used methodology. Poststratification that has been used to adjust for the sampling and coverage problems in Web surveys and is known variously as ratio adjustment, post-stratification, or cell weighting. Raking adjusts the sample weights so that sample totals line up with external population figures, but the adjustment aligns the sample to the marginal totals for the auxiliary variables, not to the cell totals.
GREG weighting is an alternative method of benchmarking sample estimates to the corresponding population figures. Another popular adjustment method is PSA or propensity weighting [13] [15] .
Poststratification, generalized regression estimation, and raking ratio estimation can be effective bias reduction techniques provided auxiliary variables are available that have a strong correlation with the target variables of the survey. If such variables cannot be used because their population distribution is not available, one might consider estimating these population distributions in a different survey, a so-called reference survey. This reference survey must be based on a probability sample, where data collection takes place with a mode different from the web, e.g., CAPI [13] .
Another possible solution for correcting the bias from selection problems is using response propensities. The response propensity is the conditional probability that a person responds to the survey request, given the available background characteristics. To compute response propensities, auxiliary information for all sample elements is needed. In particular, response propensity weighting and stratification are proposed as correction techniques.
The response propensities can be used in a direct way for estimation of the target variables directly by using the response propensities as weights. This is called response propensity weighting. The direct approach attempts to estimate the true selection probabilities by multiplying the first-order inclusion probabilities with the estimated response propensities. Bias reductions will only be successful if the available auxiliary variables are capable of explaining the response behavior. The response propensities also can be used indirectly, by forming strata of elements having the same response propensities. This is called response propensity stratification. The final estimates rely less heavily on the accuracy of the model for the response propensities.
In internet surveys, selecting a proper probability sample requires a sampling frame containing the e-mail addresses of all individuals in the population. Such sampling frames rarely exist. Actually, general-population sampling frames do not contain information about which people have internet access and which do not. Thus, one should bear in mind that people not having internet access will not respond to a internet questionnaire.
Table 2. Types of weighting adjustment methods.
Moreover, people having internet access will also not always participate. Taking these facts into account, it is evident that the ultimate group of respondents is the result of a selection process (mostly self-selected) with unknown selection probabilities.
Some studies have shown that, response propensity matching combined with response propensity stratification is a promising strategy for the adjustment of the self-selection bias in Web surveys. Research is ongoing to implement further improvements for response propensity weighting. PSA is a frequently adopted solution to improve the representativity of web panels. It should be noted that there is no guarantee that correction techniques are successful [13] . Also PSA has been suggested as an approach to adjustment for volunteer panel internet survey data. PSA attempts to decrease, if not remove, the biases arising from noncoverage, nonpro- bability sampling, and nonresponse in volunteer panel internet surveys. A few studies have examined the application of PSA for volunteer panel internet surveys [16] . PSA is used for volunteer panel internet survey by Lee, and assumed to be based on two samples:
(a) a volunteer panel survey sample (sw) with nw units each with a base weight of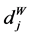 , where
, where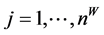 , and (b) reference survey sample (sR) with nR. Units each with a base weight of
, and (b) reference survey sample (sR) with nR. Units each with a base weight of , where
, where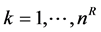 . Note that
. Note that 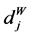 values may not be inverses of selection probabilities because probability sampling is not used. First, the two samples are combined into one,
values may not be inverses of selection probabilities because probability sampling is not used. First, the two samples are combined into one, 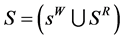 with
with  units. It is calculated propensity scores from s. The propensity score of the ith unit is the likelihood of the unit participating in the volunteer panel web survey (g = 1) rather tahn the reference survey (g = 0), where
units. It is calculated propensity scores from s. The propensity score of the ith unit is the likelihood of the unit participating in the volunteer panel web survey (g = 1) rather tahn the reference survey (g = 0), where , given auxiliary variables. Therefore, g in PSA applied to internet survey adjustment may be labeled as sample origin instead of treatment assignment. The adjusted weight for unit j in class c of the web sample becomes
, given auxiliary variables. Therefore, g in PSA applied to internet survey adjustment may be labeled as sample origin instead of treatment assignment. The adjusted weight for unit j in class c of the web sample becomes
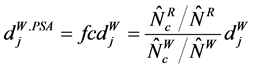 (1)
(1)
When the base weights are equal for all units or are not available, one way use an alternative adjustment factor as follows [16] ;
 (2)
(2)
Aşan & Ayhan (2013) [5] has proposed a methodology for domain weighting and adjustment procedures for free access web surveys that are based on restricted access surveys. Some basic variables can be proposed for the data adjustment, namely gender breakdown, age groups, and education groups. Within the available data sources, special adjustments are proposed for the small domains. Some basic variables can be proposed for this purpose. Adjustments can be made for age groups as well as gender breakdown as follows. Population domain sizes as


The raking formulation can be given as
where, the row adjustment will be
where, the column adjustment will be
The sum and proportion of gender (i = 1, 2) and age groups (






The application of this work consists of a first stage based on a web survey by an e-mail invitation and a second stage based on a voluntary participation internet survey. The methodology is also proposed for the estimation and allocation of the population frame characteristics of adult internet users by gender and age groups. The proposed alternative methodologies is a beneficial tool for internet survey users [5] .
6. Effectiveness of Weighting Adjustment Procedures
Several of these methods are closely related to one another. For example, post-stratification, in turn, is a special case of GREG weighting. All of the methods involve adjusting the weights assigned for the survey participants to make the sample line up more closely with population figures. A final consideration differentiating the four approaches is that propensity models can only incorporate variables that are available for both the internet survey sample and calibration sample [15] .
When we examine the effectiveness of the adjustment methods in internet surveys, some example of the works of Steinmez, Tijdens & Pedraza (2009) [17] , Tourangeau, Conrad & Couper (2013) [15] , Lee (2011) [11] , appears to be important. For example, Tourangeau, Conrad & Couper (2013) [15] presented a meta-analysis of the effect of weighting on eight online panels of nonprobability samples in order to reduce bias combining from coverage and selection effects. Among different findings, they concluded that the adjustment removed at most up to three-fifths of the bias, and that a large difference across variables still existed. In other words, after weighting, the bias was reduced for some variables but at the same time it was increased for other variables. The estimates of single variables after weighting would shift up to 20 percentage points in comparison to unweighted estimates [18] .
7. Conclusions
Internet surveys already offer enormous potential for survey researchers, and this is likely only to improve with time. In spite of their popularity, the quality of Web surveys for scientific data collection is open to discussion [19] . Many internet surveys use statistical corrections in an effort to remove, or at least reduce, the effects of coverage, nonresponse and selection biases on the estimates.
The general conclusion is that when the internet survey is based on a probability sample, nonresponse bias and, to a lesser extent, coverage bias, can be reduced through judicious use of post-survey adjustment using appropriate auxiliary variables.
The challenge for the survey industry is to conduct research on the coverage, sampling, nonresponse, and measurement error properties of the various approaches to web-based data collection. There are no corresponding sampling methods for internet surveys. As a result of these sampling difficulties, many internet surveys use self-selected samples of volunteers rather than probability samples. When it is used nonprobability sampling for internet survey, it should be used adjustment procedure.
We need to learn when the restricted population of the Web does not matter, under which conditions low response rates on the Web may still yield useful information, or how to find ways to improve response rates to internet surveys.
Cite this paper
Zerrin Asan Greenacre, (2016) The Importance of Selection Bias in Internet Surveys. Open Journal of Statistics,06,397-404. doi: 10.4236/ojs.2016.63035
References
- 1. Schonlau, M., Soest, A., Kapteyn, A. and Couper, M. (2009) Selection Bias in Web Surveys and the Use of Propensity Score. Social Methods and Research, 37, 291-318.
http://dx.doi.org/10.1177/0049124108327128 - 2. Internet World Stat. www.internetworldstats.com
- 3. Web Survey Methodology. www.websm.org
- 4. Bethlelem, J. (2008) How Accurate Are Self-Selection Web Surveys? Discussion Paper, University Amsterdam.
- 5. Asan, Z. and Ayhan, H.Ö. (2013) Sampling Frame Coverage and Domain Adjustment Procedures for Internet Surveys. Quality and Quantity, 47, 3031-3042.
http://dx.doi.org/10.1007/s11135-012-9701-8 - 6. Ayhan, H.Ö. (2000) Estimators of Vital Events in Dual—Record Systems. Journal of Applied Statistics, 27, 157-169.
http://dx.doi.org/10.1080/02664760021691 - 7. Ayhan, H.Ö. (2003) Combined Weighting Procedures for Post-Survey Adjustment in Complex Sample Surveys. Bulletin of the International Statistical Institute, 60, 53-54.
- 8. Bethlelem, J. (2008) Applied Survey Methods a Statistical Perspective. John Wiley & Sons, Hoboken.
- 9. Couper, M.P. (2011) Web Survey Methodology: Interface Design, Sampling and Statistical Inference. Instituto Vasco de Estadística (EUSTAT).
- 10. Bethlelem, J. (2010) Selection Bias in Web Survey. International Statistical Review, 78, 161-188.
http://dx.doi.org/10.1111/j.1751-5823.2010.00112.x - 11. Lee, M.H. (2011) Statistical Methods for Reducing Bias in Web Surveys.
https://www.stat.sfu.ca/content/dam/sfu/stat/alumnitheses/2011/MyoungLee_ - 12. Luth, L. (2008) An Emprical Approach to Correct Self-Selection Bias of Online Panel Research. CASRO Panel Conference.
https://luthresearch.com/wp-content/uploads/2015/12/Luth_CASRO_Paper_b08.pdf - 13. Bethlehem, J. and Biffignandi, S. (2012) Handbook of Web Surveys. John Wiley & Sons, Hoboken.
- 14. Kalton, G. and Flores-Cervantes, I. (2003) Weighting Methods. Journal of Official Statistics, 19, 81-97.
- 15. Tourangeau, R., Conrad, F. and Couper, M.P. (2013) The Science of Web Surveys. Oxford University Press, Oxford.
http://dx.doi.org/10.1093/acprof:oso/9780199747047.001.0001 - 16. Lee, S. (2006) Propensity Score Adjustment as a Weghting Scheme for Volunteer Panel Web Surveys. Journal of Offical Statistics, 22, 329-349.
- 17. Steinmetz, S., Tijdens, K. and Pedrazade, P. (2009) Comparing Different Weighting Procedures for Volunteer Web Surveys. Working paper-09-76, University of Amsterdam.
- 18. Callegaro, M., Baker, R., Bethlehem, J., Göritz, A.S., Krosnick, J.A. and Lavrakas, P.L. (2014) Online Panel Research a Data Quality Perspective. John Wiley, Hoboken.
http://dx.doi.org/10.1002/9781118763520 - 19. Lee, S. (2006). An Evaluation Nonresponse and Coverage Errors in a Prerecruited Probability Web Panel Survey. Social Science Computer Review, 24\, 460-475.
http://dx.doi.org/10.1177/0894439306288085







