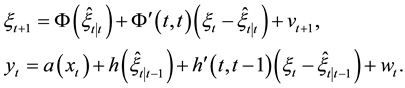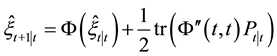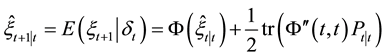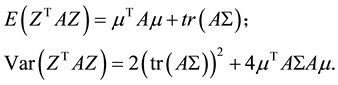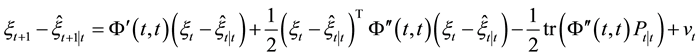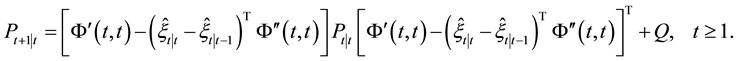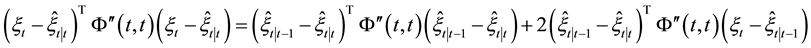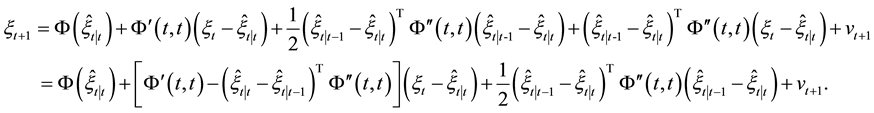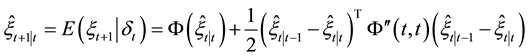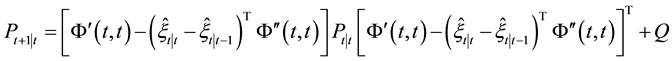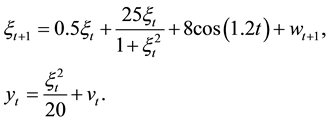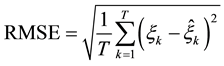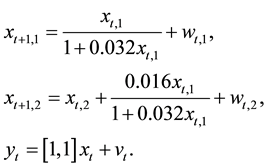Open Journal of Statistics
Vol.05 No.04(2015), Article ID:56827,7 pages
10.4236/ojs.2015.54027
Two Second-Order Nonlinear Extended Kalman Particle Filter Algorithms
Hongxiang Dai, Li Zou
Department of Statistics, Jinan University, Guangzhou, China
Email: zoulilizhixx@126.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2015; accepted 29 May 2015; published 2 June 2015
ABSTRACT
In algorithms of nonlinear Kalman filter, the so-called extended Kalman filter algorithm actually uses first-order Taylor expansion approach to transform a nonlinear system into a linear system. It is obvious that this algorithm will bring some systematic deviations because of ignoring nonlinearity of the system. This paper presents two extended Kalman filter algorithms for nonlinear systems, called second-order nonlinear Kalman particle filter algorithms, by means of second-order Taylor expansion and linearization approximation, and correspondingly two recursive formulas are derived. A simulation example is given to illustrate the effectiveness of two algorithms. It is shown that the extended Kalman particle filter algorithm based on second-order Taylor expansion has a more satisfactory performance in reducing systematic deviations and running time in comparison with the extended Kalman filter algorithm and the other second-order nonlinear Kalman particle filter algorithm.
Keywords:
Kalman Particle Filter, Nonlinear System, Taylor Expansion, Linearization Approximation

1. Introduction
It is well known that the theory of Kalman filter has been widely used in many scientific fields. Particularly, the linear Kalman filter algorithm has received a great deal of attention due to its effectiveness in estimating the state of an underlying linear system in [1] . However, it has been recognized that nonlinearity and disturbance exist in many practical linear systems, which leads to considering nonlinear Kalman filter algorithms of nonlinear state-space systems in [2] .
A widely used Kalman filter algorithm for linear systems is called extended Kalman filer algorithm (EKF for short), which actually uses first-order Taylor expansion approach to transform a nonlinear system into a linear system. Since this nonlinear Kalman filter algorithm is linear in nature and it does not consider the nonlinearity of the system equation, a sub-optimal state estimate for a nonlinear state-space system can be given in [3] . In order to reduce error in the estimation of the system state and improve the precision of EKF, various modified algorithms have been established. For example, Uhlmann et al. [4] give a kind of unscented Kalman filter (UKF) algorithm for nonlinear systems. This algorithm has the same calculation capacity as the EKF algorithm and reduces error in linearizing nonlinear model. Merwe et al. [5] present an algorithm called central difference Kalman filter (CDKF) and deduce its recursive formula. This algorithm is easier to realize than EKF, because it does not need to compute Jacobi matrices. But UKF and CDKF are not suitable for non-Gaussian state-space systems. If a state-space model is nonlinear and noise distributions are non-Gaussian, particle filters (PFs) or sequential Monte Carlo (SMC) methods provide an effective algorithm to deal with this case [6] . A combination of EKF and PF leads to extended Kalman particle filter (EKPF) algorithm, where EKF algorithm updates the sampling particles and the particles approximate the filtering distributions. The EKPF algorithm has been applied to neural networks in [7] , and the results show that the algorithm is superior to other basic particle filter algorithms. Although these algorithms have some advantages in effectiveness and calculation speed for most of nonlinear state-space models, sometimes we need some more accurate Kalman filter algorithms to estimate the state of nonlinear systems.
To this end, this paper will give two Kalman particle filter algorithms for nonlinear state-space models. One is based on second-order Taylor expansion of structural functions of nonlinear system (SEKPF), the other, denoted by SLEKPF, uses a linearization method to approximate the quadratic of second order Taylor expansion of struc- tural functions. Accordingly, recursive formulas of the above nonlinear Kalman filter algorithms are derived. A simulation example is given to compare EKPF with SEKPF and SLEKPF. It can be seen from running time and root mean square error of the state estimation that they have similar calculation capacity, but SLEKPF is superior to EKPF and SEKPE in accuracy of state estimation.
2. Nonlinear Kalman Filter
2.1. Extended Nonlinear Kalman Filter
For a nonlinear state-space model, the extended Kalman filter is a frequently used method to estimate the system state. The key point of this algorithm is to use first-order Taylor expansion to approximate the structural functions of the model. More precisely, a general nonlinear discrete-time state-space model is given as follows:
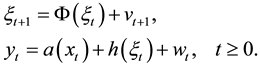
where the system state  and the noise
and the noise  are r-dimensional, whiled the observation value
are r-dimensional, whiled the observation value 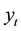 and the noise
and the noise 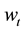 are n-dimensional. Moreover, the following assumptions are satisfied:
are n-dimensional. Moreover, the following assumptions are satisfied:
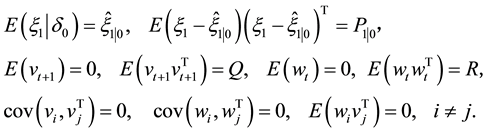
If  is a twice continuously differentiable function and
is a twice continuously differentiable function and 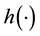 is a continuously differentiable function, then we use Taylor expansion of
is a continuously differentiable function, then we use Taylor expansion of 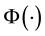 and
and 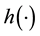 to approximate these function. In this case, the nonlinear state-space model (1) can be described approximately as a linear model. Let
to approximate these function. In this case, the nonlinear state-space model (1) can be described approximately as a linear model. Let 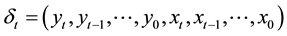 denote the information flow, namely, the observed data obtained through date
denote the information flow, namely, the observed data obtained through date 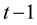 be summarized. Suppose that the initial value of the state vector
be summarized. Suppose that the initial value of the state vector 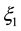 of the state-space model (1) is normally distributed and the distur-
of the state-space model (1) is normally distributed and the distur-
bances 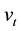 and
and 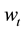 are normal. Then
are normal. Then 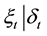 and
and 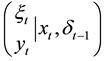
continuous first-order partial derivatives and 
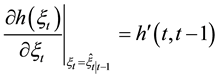
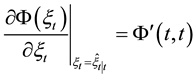
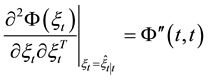
mated by linear model can be used as follows:
Proposition 2.1 If the discrete time linear system (3) satisfies (2), and the disturbances 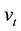
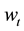
(1) state estimates
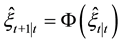
and
(2) mean square error matrix of system.
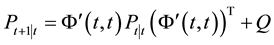
The proof of Proposition 2.1 can be found in [8] . Although the EKF algorithm is simple and effective for some nonlinear state-space models, it is likely to lead to sub-optimal state estimate due to removing higher-order terms of structural equations in Taylor expansion. In what follows, two modified nonlinear Kalman filter algorithms will be given for the purpose of reducing errors of the state estimation.
2.2. Second-Order Nonlinear Kalman Filter Algorithms
In the extended nonlinear Kalman filter algorithm, an application of first-order Taylor expansion on 
Proposition 2.2 Under the same conditions as Proposition 2.1, if 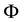
(1) state estimates are given by
and
(2) mean square error matrix of system
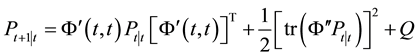
Proof: To guarantee normality of
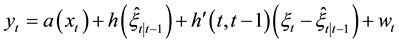
Note that 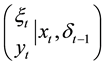
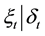
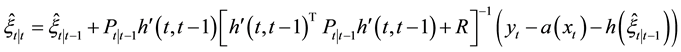
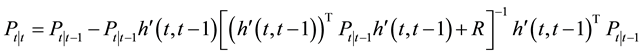
An application of Taylor expansion to 
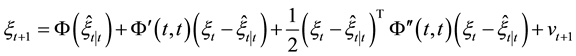
Taking conditional expectations on both sides of (5), the state estimates are given by
where we have applied the following fact that, if 
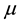
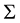
On the other hand, the residual is expressed as
Thus the mean square error matrix of system is
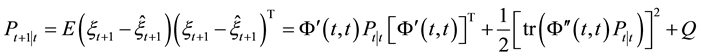
It should be pointed out that the above nonlinear Kalman filter algorithm needs to calculate Hessian matrix of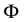
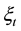
Proposition 2.3 Under the same conditions as Proposition 2.2 we have the following nonlinear Kalman filter algorithm for the nonlinear system (1):
(1) state estimates are
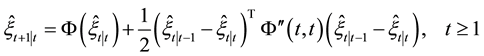
and
(2) mean square error matrix of system state is
Proof: Firstly, a second-order Taylor expansion of 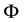
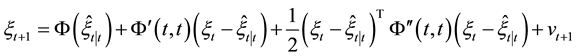
Applying first-order Taylor expansion to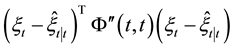
This also implies that
It is not hard to get that
Moreover, the mean square error matrix of system is given by
Note that in this nonlinear filter algorithm, we have applied first-order Taylor expansion to deal with the qua-
dratic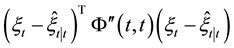
that this algorithm can give multi-step predictions of the system state.
2.3. Extended Particle Filter Algorithm
The extended particle filter (EKPF) algorithm was initially given by Freitas in [9] , under the framework of EKPF algorithm. This algorithm applies recursive formula of EKF to update each particle and will get an approximate posterior probability density of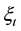
(1) Set initial value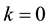
(2) Draw N particles from prior distribution (important distribution);
(3) Apply recursive formulas of EKF, SEKF, and SLEKF to update sampling particles;
(4) Update weights;
(5) Normalize weights;
(6) Resample,
(7)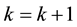
(8) If the number of particles is enough, the procedure stops.
3. Two Simulation Examples
To compare EKPF with SEKPF and SLEKPF algorithms, we use single variable non-stable growth model in [11] and gas phase reversible reaction model in [12] .
Example 3.1 Consider the following nonlinear state-space model:
where the initial state 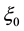
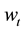
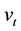
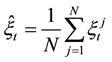
where 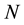
The root-mean-square error is defined as:
where T is the whole time.
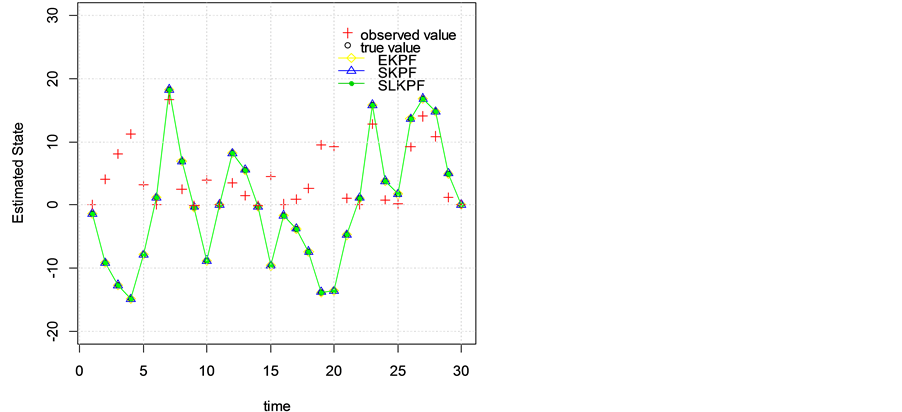
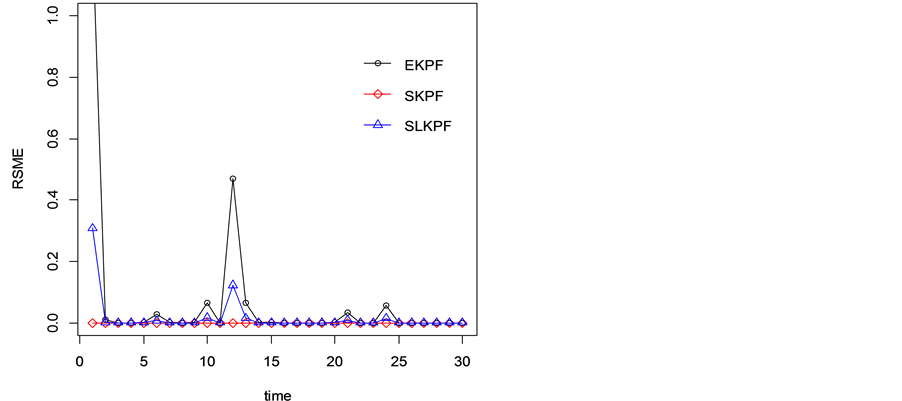
Figure 1 and Figure 2 show state estimations and the root-mean-square error curves of three kinds of algorithms. It can be seen from these figures that the EKPF algorithm is superior to other two algorithms. In particular,
Figure 1. State estimation curve of three algorithms.
Figure 2. Root mean square error curves of three algorithms.
the EKPF algorithm has the worst performance in estimating the system state. The reason lies in no consideration of higher-order Taylor expansion term. Means and variances of 100 root-mean-square errors and running time for the above particle filter algorithms are given in Table 1. The results show that the SEKPF algorithm have the minimum root-mean-square error in average. Although in three algorithms, the running time of EKPF is the shortest. We can conclude that the SEKPF and SLEKPF algorithms can effectively increase the precision of state estimations.
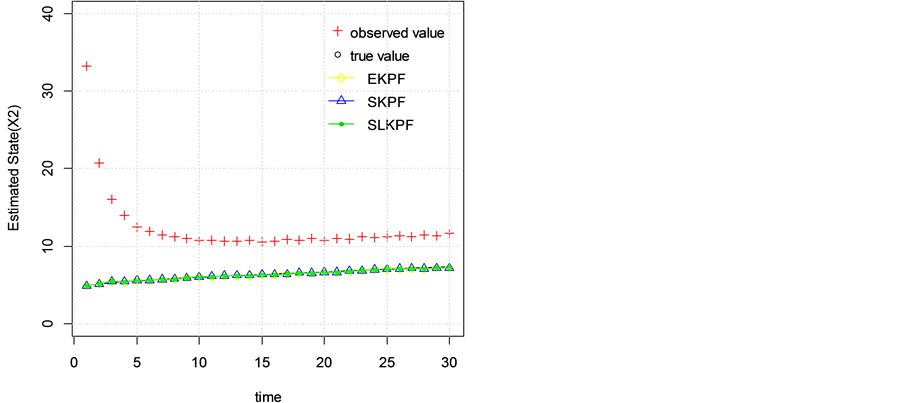
Example 3.2 Consider the following nonlinear state-space model:
where the noises w1,t and w2,t obey Gamma distributions with mean 0.5 and variance 0.5, the noise vt is normally
distributed with mean 0 and variance 0.1. We take vector 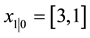
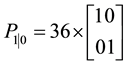
The number of particles is 200. The whole time is 30 seconds. We have 100 independent experiments.
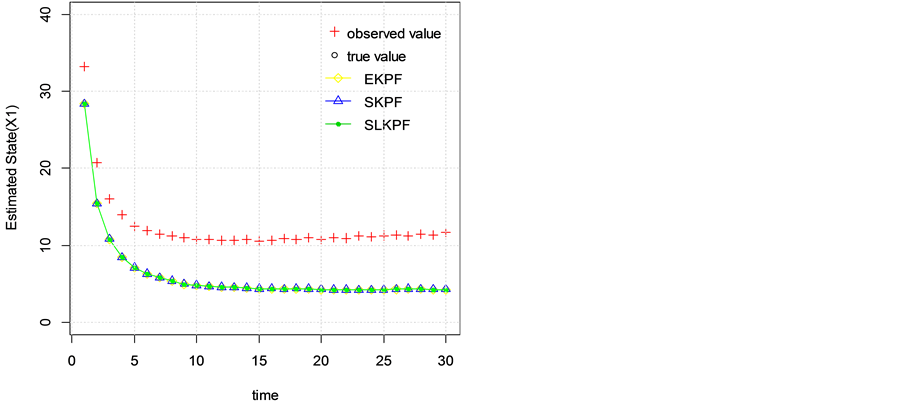
Table 2 gives means and variances of 100 independent root-mean-square errors and running time for three algorithms. Figure 3 shows state estimations of (6) obtained from three Kalman particle filter algorithms. From these, we have similar conclusions to Example 3.1. Therefore, two second-order nonlinear Kalman particle filter algorithms proposed in this paper are superior to the EKPF algorithm in the precision of state estimations.
4. Conclusion
In many practical state-space models, the observation equations are linear, but the state equations are nonlinear; sometimes the disturbances are non-Gaussian [14] . For such a state-space model, we need to give an appropriate Kalman filter algorithm to estimate the system state. In this paper, we have proposed two nonlinear Kalman filter algorithms, and corresponding recursive formulas have been derived. One is based on second-order Taylor
Table 1. Root-mean-square errors and running time of three kinds of algorithms.
Table 2. Root-mean-square errors and running time.
Figure 3. State estimate.
expansion of the state equation, and the other uses a linearization approach to approximate the quadratic of second-order Taylor expansion of the state equation. In order to improve the precision of state estimation, we have combined the above nonlinear Kalman filter algorithms with particle filter and given two nonlinear Kalman particle filter algorithms. Through two examples, we compare the two nonlinear Kalman particle filter algorithms with the extended Kalman particle filter algorithm. The simulation results show that our second-order Kalman particle filter algorithms are superior to the extended Kalman particle filter algorithm. On one hand, two nonlinear Kalman particle filter algorithms have stronger calculation capacity than the extended Kalman filter particle algorithm; on the other hand, they can effectively improve state estimations.
References
- Daum. F. (2005) Nonlinear Filters: Beyond the Kalman Filter. IEEE A&E Systems Magazine, 20, 57-69. http://dx.doi.org/10.1109/MAES.2005.1499276
- Doucet, A. and Johansen, A. (2011) A Tutorial on Particle Filtering and Smoothing: Fifteen Years Later. In: Crisan, D. and Rozovskii, B., Eds., The Oxford Handbook of Nonlinear Filtering, Oxford University Press, New York, 656-704.
- Cappe, O., Godsill, S.J. and Moulines, E. (2007) An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo. Proceedings of the IEEE, 95, 899-924. http://dx.doi.org/10.1109/JPROC.2007.893250
- Gao, Y., Gao, S. and Wu, J. (2014) Fading-Memory Square-Root Unscented Particle Filter Algorithm and Its Application in Integrated Navigation System. Journal of Chinese Inertial Technology, 22, 777-781.
- Qian, Z. and Qi, Y. (2012) A SLAM Algorithm Based on an Iterated Central Difference Particle Filter. Journal of Harbin Engineering University, 33, 355-360.
- Zhu, Z. (2012) Particle Filter Algorithm and Application. Science Press, Beijing.
- Wang, F. and Guo, Q. (2010) Neural Network Training Based on Extended Kalman Particle Filter. Computer Engineering & Science, 32, 48:50.
- Zhao, L. (2012) Nonlinear Kalman Filter Theory. National Defense Industry Press, Beijing.
- Julier, S.J., Uhlmann, J.K. and Durrant-Whyten, H.F. (2000) A New Approach for the Nonlinear Transformation of Means and Covariance in Filters and Estimators. IEEE Transactions on Automatic Control, 45, 477-482. http://dx.doi.org/10.1109/9.847726
- Wang, F. and Zhao, Q. (2008) A New Particles to Solve the Problem of Nonlinear Filter Algorithm. Chinese Journal of Computers, 31, 346-352.
- Liu, X., Tao, Z., Jin, Y. and Yang, Y. (2010) A Novel Multiple Model Particle Filter Algorithm Based on Particle Optimization. Acta Electronica Sinica, 38, 301-305.
- Kolas, S., Foss, B.A. and Schei, T.S. (2009) Constrained Nonlinear State Estimation-Based on the UKF Approach. Computers & Chemical Engineering, 33, 1386-1401. http://dx.doi.org/10.1016/j.compchemeng.2009.01.012
- Wang, F., Lu, M., Zhao, Q. and Yuan, Z. (2014) Particle Filtering Algorithm. Chinese Journal of Computers, 37, 1679-1693.
- Xia, N., Qiu, T. and Li, J. (2013) A Nonlinear Kalman Filtering Algorithm Combining the Kalman Filter and the Particle Filter. Acta Electronica Sinica, 41, 148-152.