Open Journal of Discrete Mathematics
Vol.05 No.04(2015), Article ID:60694,6 pages
10.4236/ojdm.2015.54008
Domination Number of Square of Cartesian Products of Cycles
Morteza Alishahi, Sakineh Hoseini Shalmaee
Islamic Azad University, Nazarabad Branch
Email: morteza.alishahi@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 August 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
A set 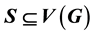 is a dominating set of G if every vertex of
is a dominating set of G if every vertex of 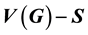 is adjacent to at least one vertex of S. The cardinality of the smallest dominating set of G is called the domination number of G. The square G2 of a graph G is obtained from G by adding new edges between every two vertices having distance 2 in G. In this paper we study the domination number of square of graphs, find a bound for domination number of square of Cartesian product of cycles, and find the exact value for some of them.
is adjacent to at least one vertex of S. The cardinality of the smallest dominating set of G is called the domination number of G. The square G2 of a graph G is obtained from G by adding new edges between every two vertices having distance 2 in G. In this paper we study the domination number of square of graphs, find a bound for domination number of square of Cartesian product of cycles, and find the exact value for some of them.
Keywords:
Domination Number, Square of a Graph, Cartesian Product

1. Introduction
The usual graph theory notions not herein, refer to [1] . The neighborhood of vertex u is denoted by 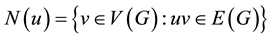 and the close neighborhood of vertex u is denoted by
and the close neighborhood of vertex u is denoted by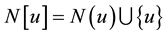 . Let
. Let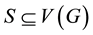 , the neighborhood and closed neighborhood of S are defined as
, the neighborhood and closed neighborhood of S are defined as  and
and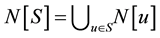 . If
. If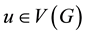 , then
, then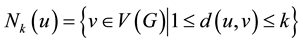 . If
. If 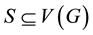 and
and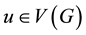 ,
,
then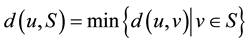 . The diameter of G denoted by
. The diameter of G denoted by 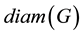 is defined as
is defined as 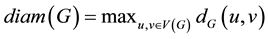 . A set
. A set 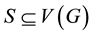 is a dominating set of G if every vertex of
is a dominating set of G if every vertex of 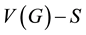 is adjacent to at least one vertex of S. The cardinality of the smallest dominating set of G, denoted by
is adjacent to at least one vertex of S. The cardinality of the smallest dominating set of G, denoted by









dominating set of


graph with vertex set 


locating copies 









2. Preliminaries Results
Theorem 1. Let G be a graph. Then
a) If

b) If

Proof. a) Every dominating set of 

b) Every dominating set of G is a dominating set of 

Theorem 2. [3] A dominating set S is a minimal dominating set if and only if for each vertex
a) u is an isolated vertex of S.
b) there exist a vertex 

Theorem 3. [3] If G is a graph with no isolated vertices and S is a minimal dominating set of G, then 
Proof. Let S be a g-set of G. S is a minimal dominating set of G. By Theorem 3, 


Theorem 4. [4] If G is a connected claw free graph, then
Theorem 5. [5] Let G be a graph. Then
Since
Corollary 6.
Vizing conjecture
Let G and H be two graphs. Then 
3. Domination Number of Square of Graphs
Theorem 7. Let S be a dominating set of


a) There exists a vertex 

b) 

Proof. If 









Theorem 8. If

Proof. Let




Theorem 9. If


Proof. Let u be an arbitrary vertex of G. Let








Theorem 10. Let G be a graph. Then
Proof. Let 









Theorem 11. For every

Proof. The graphs 













Theorem 12. For every

Proof.




is a dominating set of size 



Theorem 13. For every



Proof. The graphs 



By Theorem 13, 



Figure 1. A dominating set of
Figure 2. A dominating set of
Figure 3. Dominated vertices by u in 

Figure 4. Dominated vertices by one vertex in 

In this paper we use short display or s.d to show the graphs 

Theorem 14. For every

Proof. By Theorem 13 we have




We can obtain s.d of 


Figure 5. A dominating set of size 13 for

Theorem 15.

Proof. Since
Theorem 16.

Proof. By Theorem 13 we have




In Figure 6, the seventh column of s.d of 






















Theorem 17.

Proof. By Theorem 13 we have
Figure 6. A dominating set for

Figure 7. A dominating set for


By Figure 7 we have

In Figure 7, the seventh column of s.d of 


























Cite this paper
MortezaAlishahi,Sakineh HoseiniShalmaee, (2015) Domination Number of Square of Cartesian Products of Cycles. Open Journal of Discrete Mathematics,05,88-94. doi: 10.4236/ojdm.2015.54008
References
- 1. West, D.B. (2001) Introduction to Graph Theory. 2nd Edition, Prentice-Hall, Upper Saddle River.
- 2. Haynes, T., Hedetniemi, S. and Slater, P.J. (1997) Fundamentals of Domination in Graphs. M. dekker, Inc., New York.
- 3. Ore, O. (1962) Theory of Graphs. American Mathematical Society Colloquium Publications, 38 (American Mathematical Society, Providence, RI).
- 4. Cockayne, E.J., Ko, C.W. and Shepherd, F.B. (1985) Inequalities Concerning Dominating Sets in Graphs. Technical Report DM-370-IR, Department of Mathematics, University of Victoria.
- 5. Walikar, H.B., Acharya, B.D. and Sampathkumar, E. (1979) Recent Developments in the Theory of Domination in Graphs. In MRI Lecture Notes in Math. Mehta Research Institute of Mathematics, Allahabad, Vol. 1.
- 6. Vizing, V.G. (1963) The Cartesian Product of Graphs. Vycisl. Sistemy, 9, 30-43.














