Open Journal of Discrete Mathematics
Vol.2 No.2(2012), Article ID:18868,4 pages DOI:10.4236/ojdm.2012.22010
Quasi-Kernels for Oriented Paths and Cycles
Department of Mathematics, Allegheny College, Meadville, USA
Email: sbowser@allegheny.edu
Received February 2, 2012; revised March 2, 2012; accepted March 21, 2012
Keywords: digraph; quasi-kernel; path; cycle
ABSTRACT
If D is a digraph, then 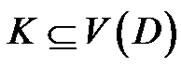 is a quasi-kernel of D if
is a quasi-kernel of D if  is discrete and for each
is discrete and for each 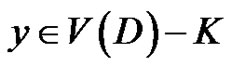 there is
there is 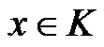 such that the directed distance from y to x is less than three. We give formulae for the number of quasi-kernels and for the number of minimal quasi-kernels of oriented paths and cycles.
such that the directed distance from y to x is less than three. We give formulae for the number of quasi-kernels and for the number of minimal quasi-kernels of oriented paths and cycles.
1. Introduction
Notation For a digraph D, 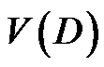 and
and  denote its vertex set and arc set, respectively. If
denote its vertex set and arc set, respectively. If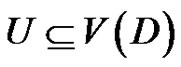 , then
, then  denotes the subdigraph of D induced by U and
denotes the subdigraph of D induced by U and 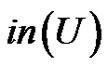 and
and 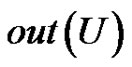 denote, respectively, the inand out-neighborhoods of U. If
denote, respectively, the inand out-neighborhoods of U. If , these latter sets may be written
, these latter sets may be written  and
and .
.
Definition 1 A quasi-kernel K of a digraph D is a subset of  satisfying two properties:
satisfying two properties:
1) The quasi-absorbing property: 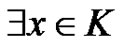
 such that the directed distance in D from y to x is either one or two;
such that the directed distance in D from y to x is either one or two;
2) Independence: there is no arc in 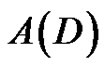 between vertices of K.
between vertices of K.
If K is a quasi-kernel for digraph D,  and
and  and the directed distance from y to x in D is either one or two, then we will say that x quasi-absorbs y.
and the directed distance from y to x in D is either one or two, then we will say that x quasi-absorbs y.
By [1], every digraph has at least one quasi-kernel. The number of quasi-kernels possessed by various classes of digraphs has been addressed in several papers. For example, in [2] Gutin et al. give necessary and sufficient conditions for a digraph to have at least three quasi-kernels. Clearly, any independent superset of a quasi-kernel is a quasi-kernel. In [3] we give sufficient conditions for a digraph to have at least three minimal quasi-kernels. In [4], Heard and Huang provide sufficient conditions for at least three disjoint quasi-kernels in certain classes of digraphs. In the present work, we address the problem of counting the number of quasi-kernels and the number of minimal quasi-kernels of oriented paths and cycles.
Notation For a digraph D, 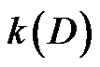 denotes the number of distinct quasi-kernels of D and
denotes the number of distinct quasi-kernels of D and  denotes the number of minimal quasi-kernels of D.
denotes the number of minimal quasi-kernels of D.
Our approach is to recursively construct all quasikernels and all minimal quasi-kernels of various classes of digraphs in order to count them. The following general lemma will be useful for the examination of these special classes.
Lemma 1 If D1 and D2 are digraphs such that , where x is a sink in both
, where x is a sink in both 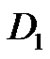 and
and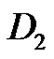 , then
, then  and
and .
.
Proof. Using the notation from the statement of the lemma, if  is a quasi-kernel for
is a quasi-kernel for  for
for , then
, then  clearly satisfies the quasi-absorbing property for
clearly satisfies the quasi-absorbing property for 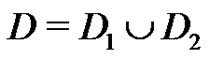 and D has no arcs between a vertex of
and D has no arcs between a vertex of 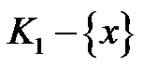 and one of
and one of , so K inherits independence from
, so K inherits independence from 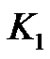 and
and . It follows that
. It follows that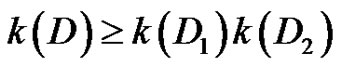 .
.
If on the other hand, K is a quasi-kernel of 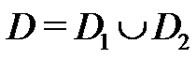 and
and  for
for , then clearly both K1 and K2 are independent. Since x is a sink in D, a directed path in D lies completely in D1 or D2. Thus the quasiabsorbing property is satisfied by K1 in D1 and by K2 in D2. It follows that every quasi-kernel of D arises as the union of a quasi-kernel of D1 and one of D2, so
, then clearly both K1 and K2 are independent. Since x is a sink in D, a directed path in D lies completely in D1 or D2. Thus the quasiabsorbing property is satisfied by K1 in D1 and by K2 in D2. It follows that every quasi-kernel of D arises as the union of a quasi-kernel of D1 and one of D2, so . It is clear that K1 and K2 are both minimal for D1 and D2 respectively iff
. It is clear that K1 and K2 are both minimal for D1 and D2 respectively iff  is minimal for
is minimal for , so
, so .
.
2. Paths
By Lemma 1, to count the number of quasi-kernels in an arbitrary oriented path, it suffices to consider those with no internal sinks, i.e. the digraphs  and
and 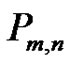 defined below.
defined below.
Notation
1)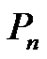 denotes the directed path on vertices
denotes the directed path on vertices with arc set
with arc set .
.
2) For ,
, 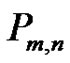 denotes the result of identifying the source vertices of
denotes the result of identifying the source vertices of  and
and . We will denote the vertices
. We will denote the vertices 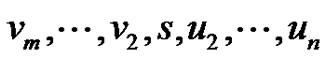 where
where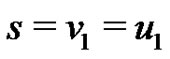 , and
, and , and
, and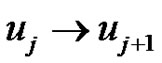 .
.
3)  denotes the number of quasi-kernels of
denotes the number of quasi-kernels of  containing the vertex
containing the vertex .
.
There are two quasi-kernels of  containing
containing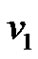 , viz.
, viz.  and
and , thus
, thus  The results we obtain will be expressed in terms of the e function, so our first goal is to obtain a closed-form expression for its value. We start with a useful recursion relation.
The results we obtain will be expressed in terms of the e function, so our first goal is to obtain a closed-form expression for its value. We start with a useful recursion relation.
Lemma 2 If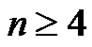 , then
, then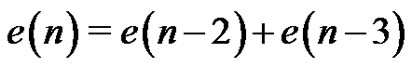 .
.
Proof. If K is a quasi-kernel of  containing v1, then, by the quasi-absorbing property, K must contain either v3 or v4 and, by independence, K cannot contain both, nor can it contain the vertex v2. The equation follows.
containing v1, then, by the quasi-absorbing property, K must contain either v3 or v4 and, by independence, K cannot contain both, nor can it contain the vertex v2. The equation follows.
For some of what follows, it is convenient to extend the domain of the function e using the above recursion relation backwards. Thus, since  and
and , we set
, we set 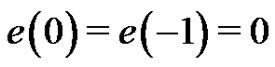 and the recursion relation as stated in Lemma 2 holds for
and the recursion relation as stated in Lemma 2 holds for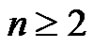 .
.
It is straightforward to confirm that the characteristic equation of the above recursion relation, 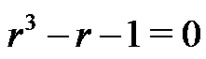 , has the following roots:
, has the following roots:

where

The solution of the recursion relation can be written , where x1, x2 and x3 are selected to satisfy the initial conditions
, where x1, x2 and x3 are selected to satisfy the initial conditions 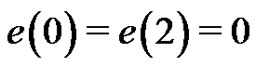 and
and . The straightforward solution of the
. The straightforward solution of the 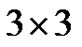 system provides the following solution. (The identity
system provides the following solution. (The identity  was used in obtaining these expressions.)
was used in obtaining these expressions.)
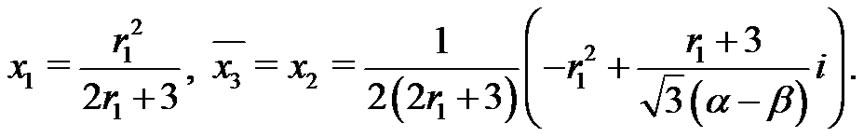
Theorem 1 For ,
, 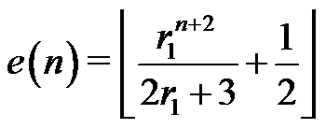
Proof. Notice that

So, since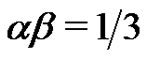 ,
,

It can also be shown that . (We omit the details, but this follows in a straightforward way, making use of the facts that
. (We omit the details, but this follows in a straightforward way, making use of the facts that

and that . Thus, for all
. Thus, for all ,
,
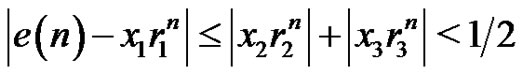 .
.
Since  is integer valued, the result follows.
is integer valued, the result follows.
Theorem 2 For all integers 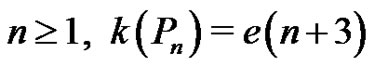 and
and 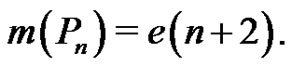
Proof. By the quasi-absorbing property, the first vertex of a quasi-kernel of  for
for  must be v1, v2, or v3, thus
must be v1, v2, or v3, thus . Using Lemma 2 twice produces the desired equation. The first two values of n can be considered directly:
. Using Lemma 2 twice produces the desired equation. The first two values of n can be considered directly:
 .
.
The only quasi-kernels of  which are not minimal are those that contain both v1 and v3. There are clearly
which are not minimal are those that contain both v1 and v3. There are clearly 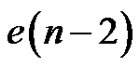 of these, so
of these, so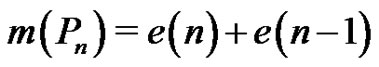 . Again, the recursion relation produces the desired result.
. Again, the recursion relation produces the desired result.
Theorem 3 For all integers ,
,
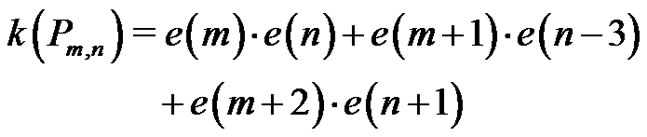
Proof. As noted in its definition, the digraph 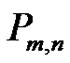 contains subdigraphs isomorphic to
contains subdigraphs isomorphic to 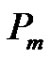 and
and . We will abuse the notation by using
. We will abuse the notation by using  and
and  to denote subgraphs induced by
to denote subgraphs induced by  and
and , respectively. The set of all quasi-kernels of
, respectively. The set of all quasi-kernels of  can be partitioned according to how the quasi-absorbing property is satisfied for the vertex s. Let K be a quasi-kernel of
can be partitioned according to how the quasi-absorbing property is satisfied for the vertex s. Let K be a quasi-kernel of  and consider cases.
and consider cases.
1) K contains s.
In this case  is a quasi-kernel of
is a quasi-kernel of  containing
containing  and
and 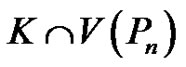 is a quasi-kernel of
is a quasi-kernel of  containing
containing  Thus, this case contributes
Thus, this case contributes 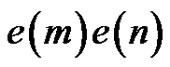 quasi-kernels of
quasi-kernels of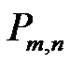 .
.
2) K contains v2 or v3, but not s, u2, nor u3.
Note that the quasi-absorbing property requires that . In this case
. In this case 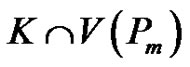 is one of the
is one of the  quasi-kernels of
quasi-kernels of 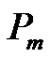 with first vertex either v2 or v3 and
with first vertex either v2 or v3 and  is one of the
is one of the  quasi-kernes of the subgraph of
quasi-kernes of the subgraph of  induced by
induced by  containing
containing . There are
. There are
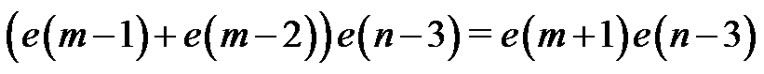
such sets K.
3) K contains u2 or u3, but not s = v1, v2 nor v3.
This is the preceding case with m and n reversed. It contributes 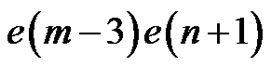 additional quasi-kernels.
additional quasi-kernels.
4) K contains one vertex from  and one from
and one from  but does not contain s.
but does not contain s.
Here,  is one of the
is one of the 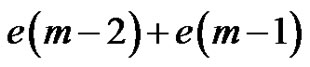 quasi-kernels of
quasi-kernels of  not containing
not containing  and
and  is a quasi-kernel of
is a quasi-kernel of  not containing
not containing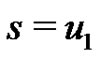 , of which there are
, of which there are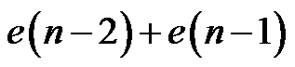 . Thus we have a final
. Thus we have a final

quasi-kernels.
Summing the contributions over this mutually exclusive and exhaustive list of cases:
 .
.
The last two terms can be combined using Lemma 2 since

Theorem 4 For all integers ,
,
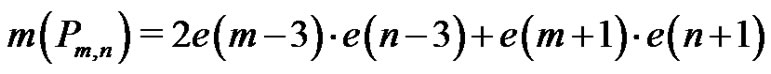
Proof. Throughout this proof we follow the notation introduced on page 2. Note first that any quasi-kernel of  containing the source (s) and also either v3 or u3 is not minimal. On the other hand, any quasi-kernel containing the source but contains neither v3 nor u3 must contain both v4 and u4. It is easy to see that such a quasikernel is minimal. Thus there are
containing the source (s) and also either v3 or u3 is not minimal. On the other hand, any quasi-kernel containing the source but contains neither v3 nor u3 must contain both v4 and u4. It is easy to see that such a quasikernel is minimal. Thus there are 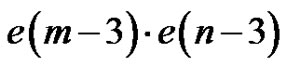 minimal quasi-kernels containing the source.
minimal quasi-kernels containing the source.
The table in Figure 1 depicts the relevant fragments of all possible quasi-kernels not containing the source. The possiblilities are sorted according to the subscripts on the v’s and secondarily to the subscript on the u’s. The leftmost column enumerates the cases for reference herein. The right-most column gives, in the case of a non-minimal quasi-kernel, an example of an extraneous vertex and, otherwise, the number of minimal quasi-kernels containing the given fragment. For example in case 1, v2 could be removed from a quasi-kernel containing that fragment and leave a set which is still a quasi-kernel whereas in case 8, the given fragment could be extended by any of the  quasi-kernels of
quasi-kernels of  containing v5 and, independently, any of the
containing v5 and, independently, any of the 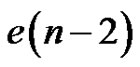 quasi-kernels of
quasi-kernels of  containing u3 to yield a minimal quasi-kernel of
containing u3 to yield a minimal quasi-kernel of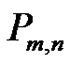 . Certain of the vertices have been left off the table if their presence in the minimal quasi-kernel is neither mandatory nor forbidden in the case depicted. For example in row 7, u5 is not depicted since, in the configuration shown, it is present in some minimal quasi-kernels and absent in others.
. Certain of the vertices have been left off the table if their presence in the minimal quasi-kernel is neither mandatory nor forbidden in the case depicted. For example in row 7, u5 is not depicted since, in the configuration shown, it is present in some minimal quasi-kernels and absent in others.
Lemma 2 can be used to simplify the sum of the terms in the right column which contribute to . Thus, rows 6-8 sum to
. Thus, rows 6-8 sum to , rows 10-12 sum to
, rows 10-12 sum to 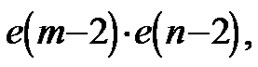 and rows 13 - 14 sum to
and rows 13 - 14 sum to  The last two of these expressions sum to
The last two of these expressions sum to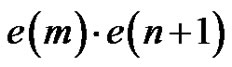 , and thus we have the number of minimal quasi-kernels of
, and thus we have the number of minimal quasi-kernels of  which do not contain the source:
which do not contain the source:

Figure 1. Pm,n.
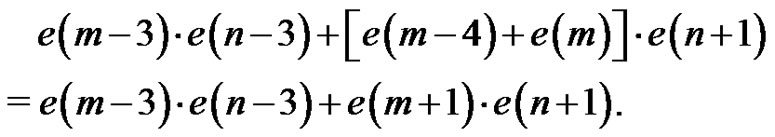
Combining this with the number already obtained for those that contain the source gives the desired result.
As stated at the beginning of this section, Theorems 2, 3 and 4 used with Lemma 1 provide the number of quasikernels and the number of minimal quasi-kernels for arbitrary oriented paths.
3. Cycles
Counting quasi-kernels for oriented cycles can almost be reduced to counting those of oriented paths. Of course any oriented cycle can be obtained by identifying the “leaf” vertices of an oriented path. The reverse process we shall call “splitting”.
Theorem 5 If x is a sink of a oriented cycle C and P is the oriented path obtained by splitting C at x, then  and
and .
.
Proof. Let the two vertices of P whose identification produce x in C be 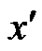 and
and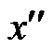 . Every quasi-kernel of a digraph must contain all the sinks of that digraph, so K is a quasi-kernel of C iff
. Every quasi-kernel of a digraph must contain all the sinks of that digraph, so K is a quasi-kernel of C iff 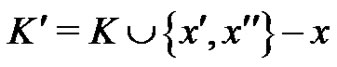 is a quasikernel of P. In particular, K is minimal for C iff
is a quasikernel of P. In particular, K is minimal for C iff 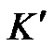 is minimal for P. The result follows.
is minimal for P. The result follows.
Theorem 6 If C is a oriented cycle of order n with no sink, then .
.
Proof. Observe first that every quasi-kernel of such a C is minimal, so . C is the result of identifying vertices v1 and
. C is the result of identifying vertices v1 and  of
of . Use the vertex names from
. Use the vertex names from  (v1 for the identified vertices). If
(v1 for the identified vertices). If  and K is a quasi-kernel for C, then there are three possibilities.
and K is a quasi-kernel for C, then there are three possibilities.
1) K contains v1.
These quasi-kernels are exactly the images under the identification above of a quasi-kernel of  containing v1. There are
containing v1. There are 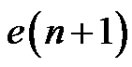 of these.
of these.
2) K contains v2.
Again, there are 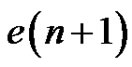 such quasi-kernels.
such quasi-kernels.
3) K contains v3 but not v1.
Since K contains neither v1 nor v2, it must contain vn. There are therefore 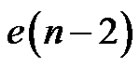 such quasi-kernels.
such quasi-kernels.
The quasi-absorbing property requires that K contain at least one of the vertices v1, v2 and v3. On the other hand, independence ensures that the cases above are mutually exclusive.
REFERENCES
- V. Chvátal and L. Lovász, “Every Directed Graph Has a Semi-Kernel,” Hypergraph Seminar, Lecture Notes in Mathematics, Vol. 441, Springer-Verlag, Berlin, 1974, p. 175.
- G. Gutin, K. M. Koh, E. G. Tay and A. Yeo, “On the Number of Quasi-Kernels in Digraphs,” Journal of Graph Theory, Vol. 46, No. 1, 2004, pp. 48-56. doi:10.1002/jgt.10169
- S. Bowser and C. Cable, “At Least Three Minimal Quasi-Kernels,” Discrete Applied Mathematics, Vol. 160, No. 4-5, 2012, pp. 673-675. doi:10.1016/j.dam.2011.08.017
- S. Heard and J. Huang, “Disjoint Quasi-Kernels in Digraphs,” Journal of Graph Theory, Vol. 58, No. 3, 2008, pp. 251-260. doi:10.1002/jgt.20310

