Theoretical Economics Letters
Vol. 2 No. 5 (2012) , Article ID: 25935 , 4 pages DOI:10.4236/tel.2012.25104
On the Concavity of the Consumption Function with a Quadratic Utility under Liquidity Constraints
1Tohoku University, Sendai, Japan
2Bank of Japan, Tokyo, Japan
Email: nishiyama@econ.tohoku.ac.jp, ryou.katou@boj.or.jp
Received April 26, 2012; revised May 28, 2012; accepted June 3, 2012
Keywords: Consumption Function, Liquidity Constraints
ABSTRACT
This paper demonstrates the concavity of the consumption function of infinitely living households under liquidity constraints who are not prudent—i.e. with a quadratic utility. The concavity of the consumption function is closely related to the 3-convexity of the value function.
1. Introduction
Since the numerical illustration by Deaton [1], researchers have been aware that liquidity constraints generate a concavity in the consumption function. However, analytics of the concavity due to liquidity constraints has remained unknown until recently. Carroll and Kimball [2] made the first important attempt in setting an analytical foundation and showed the concavity of the consumption function when the consumer’s optimization has a finite horizon. Technically, they exploit the convexity of marginal value function in the terminal period and use the backward induction to show the convexity of marginal value function in the current period. However, in the context of infinite horizon, this particular approach is not applicable since the terminal period’s value function is not defined.
In this paper, we offer an analytical foundation of the concavity of the consumption function in the context of infinite horizon, when consumer’s utility is quadratic. Taking a different approach to Carroll and Kimball [2], we directly prove the 3-convexity or Levinson’s Inequality (Levinson [3]) of the value function and show that the consumption function is concave. The concept of 3-convexity is extremely convenient when characterizing the value function, especially with the infinite horizon. Thus, we regard this 3-convexity approach as a complement, rather than a substitute, to Carroll and Kimball’s [2] backward induction approach in the finite horizon setting.
Finally, it should be emphasized that under the model that we consider—i.e. consumer’s utility is quadratic— the concavity is not generated by prudence of the consumer, but is solely generated by the presence of liquidity constraints1. By the virtue of this set-up, we can solely focus on the analytical mechanism how liquidity constraints generate the concavity in the consumption function. The rest of the paper is organized as follows. Sectiones 2 discuss the set-up of the model. Section 3 clarifies the concept of 3-convexity, shows the 3-convexity of the value function and proves the concavity of the consumption function. Section 4 provides some concluding remarks.
2. The Model
We assume a very simple infinite horizon dynamic optimization problem where consumer’s utility is quadratic and time-separable. Further, consumer faces no uncertainty in terms of rate-of-return on the net wealth and in terms of labor income. The only source that makes the dynamic optimization problem non-standard is the existence of liquidity constraints—the net wealth cannot be negative. Thus, consumer’s dynamic optimization problem can be formulated as follows.
 (1)
(1)


where  stands for consumption, which is the control variable of the consumer, and
stands for consumption, which is the control variable of the consumer, and  stands for the net wealth, which is the state variable of the optimization problem. Period-by-period utility is defined as a quadratic function in consumption, i.e.
stands for the net wealth, which is the state variable of the optimization problem. Period-by-period utility is defined as a quadratic function in consumption, i.e. , where
, where  and
and  are positive constant parameters. Discount rate
are positive constant parameters. Discount rate  interest rate
interest rate , and labor income
, and labor income , are assumed to be time-invariant2. Recursive nature of this infinite horizon problem allows us to reduce it into the following Bellman equation:
, are assumed to be time-invariant2. Recursive nature of this infinite horizon problem allows us to reduce it into the following Bellman equation:
 (2)
(2)

It should be noted that since the optimization horizon is infinite, the value functions in the subsequent period will converge to a certain function 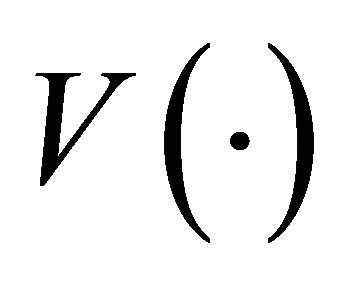 as can be seen on both sides of the Bellman Equation (2). Furthermore, this converged value function is a consequence of recursive optimization under liquidity constraints from the future period and therefore should be distinguished from the value function under liquidity unconstrained case3. In other words, the value function under liquidity constraints will no longer be a quadratic function even under quadratic utility, which is in sharp contrast to the case without liquidity constraint whose value function is, of course, quadratic.
as can be seen on both sides of the Bellman Equation (2). Furthermore, this converged value function is a consequence of recursive optimization under liquidity constraints from the future period and therefore should be distinguished from the value function under liquidity unconstrained case3. In other words, the value function under liquidity constraints will no longer be a quadratic function even under quadratic utility, which is in sharp contrast to the case without liquidity constraint whose value function is, of course, quadratic.
Taking the first-order condition of Equation (2) with respect to consumption will yield the following equation:
 (3)
(3)
The function  on the left-hand side characterizes the optimal consumption as a function of the current net wealth. Further, by invoking the envelope theorem (or Benveniste-Scheinkman formula) on Equation (2), we can derive the following relation between the current shadow price of the net wealth—i.e. the marginal value function evaluated at the current net wealth—and the future shadow price.
on the left-hand side characterizes the optimal consumption as a function of the current net wealth. Further, by invoking the envelope theorem (or Benveniste-Scheinkman formula) on Equation (2), we can derive the following relation between the current shadow price of the net wealth—i.e. the marginal value function evaluated at the current net wealth—and the future shadow price.
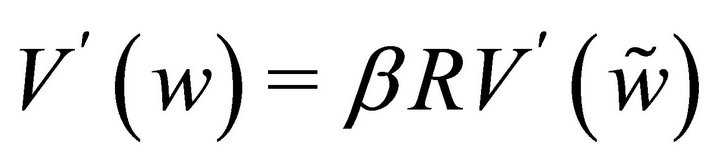 (4)
(4)
Combining Equations (3) and (4), we obtain the following key equation:
 (5)
(5)
The virtue of Equation (5) is that it relates the current optimal consumption to the current shadow price of the net wealth rather than the future shadow price of the net wealth as in Equation (3). This key relationship enables us to infer the characteristics of the optimal consumption function by investigating the nature of the marginal value function. Or putting it another way, it suffices to characterize the marginal value function in order to characterize the optimal consumption function4.
Some remarks are in order. If the value function is three times differentiable, then 3-convexity of the value function is equivalent to positiveness of the third derivative of the value function—i.e., . However, as pointed out by Carroll and Kimball [2], the marginal value function in Equation (5) is “kinked” under the deterministic environment with liquidity constraints that
. However, as pointed out by Carroll and Kimball [2], the marginal value function in Equation (5) is “kinked” under the deterministic environment with liquidity constraints that  is not well defined. Thus, it is not appropriate to rely on third order differentiability of
is not well defined. Thus, it is not appropriate to rely on third order differentiability of  in proving the concavity of the consumption function, especially in our case of consideration. Fortunately, the concept of 3-convexity is more general in its applicability. As long as the value function is once differentiable, 3-convexity implies the convexity of marginal value function even if the marginal value function is kinked and this implication does not require the function to be 2 or 3 times differentiable. It is this property of 3-convexity that makes it relatively easy to show the concavity of the consumption function in the presence of liquidity constraints. The following section clarifies the concept of 3-convexity and then shows that the value function is 3-convex.
in proving the concavity of the consumption function, especially in our case of consideration. Fortunately, the concept of 3-convexity is more general in its applicability. As long as the value function is once differentiable, 3-convexity implies the convexity of marginal value function even if the marginal value function is kinked and this implication does not require the function to be 2 or 3 times differentiable. It is this property of 3-convexity that makes it relatively easy to show the concavity of the consumption function in the presence of liquidity constraints. The following section clarifies the concept of 3-convexity and then shows that the value function is 3-convex.
3. Main Results
We first define the notion of 3-convexity.
Definition 1 (3-convexity). A function  is said to be 3-convex on
is said to be 3-convex on  if for
if for 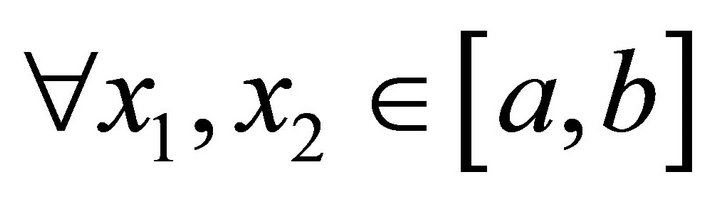 such that
such that 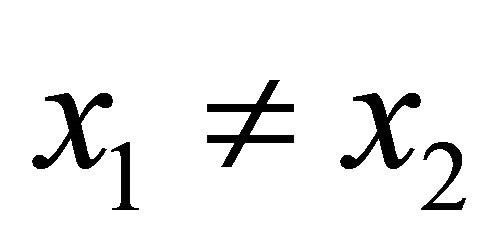
 (6)
(6)
The inequality (6) is a special case of Levinson’s inequality (Levinson [3]) which can be regarded as a higher-order Jensen’s inequality. As Jensen’s inequality is closely related with the notion of convexity, so is Levinson’s inequality with 3-convexity. The intuition of the inequality (6) can be vividly captured by Figure 1. The left-hand side of the inequality (i.e. denoted ) represents the difference between the value of function
) represents the difference between the value of function
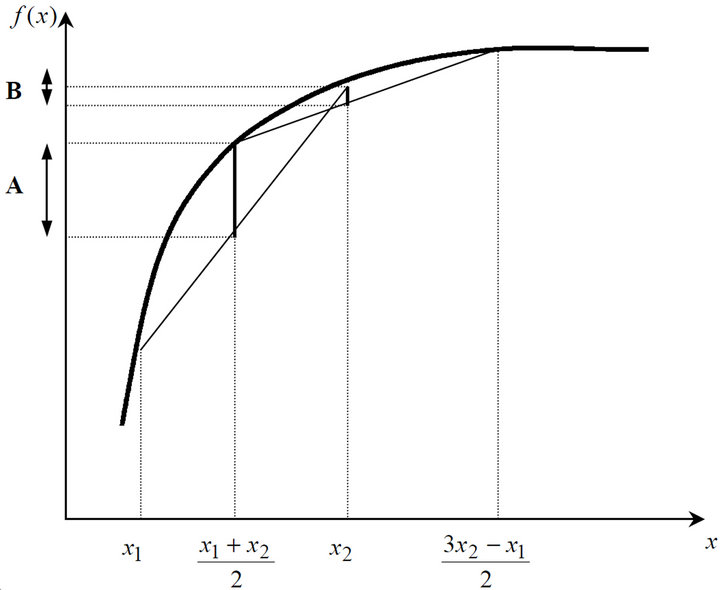
Figure 1. Illustration of 3-convexity.
evaluated at the mid-point of  and
and  to the midpoint of the chord from
to the midpoint of the chord from  and
and . It is possible to interpret
. It is possible to interpret  as a magnitude of concavity of a function in the domain
as a magnitude of concavity of a function in the domain . The right-hand side of the inequality (i.e. denoted
. The right-hand side of the inequality (i.e. denoted ) can be interpreted in the similar fashion with a difference that domain is now
) can be interpreted in the similar fashion with a difference that domain is now
 .
.
Thus, intuitively speaking, the function will be 3-convex if the magnitude of concavity decreases as  increases5.
increases5.
Next, we state the lemma that links 3-convexity of the function to convexity of the marginal function. The following lemma is a special case of the more general theorem that links  -convexity to convexity of
-convexity to convexity of  th derivative of a function. Rigorous proof of the theorem is well beyond the scope of this paper and will be omitted.
th derivative of a function. Rigorous proof of the theorem is well beyond the scope of this paper and will be omitted.
Lemma 1. If a function  is 3-convex on
is 3-convex on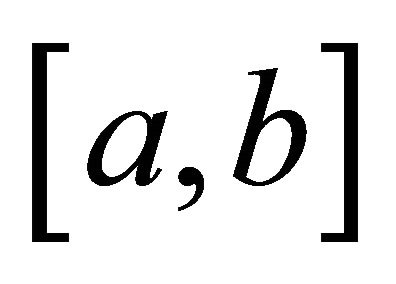 , then the first derivative
, then the first derivative 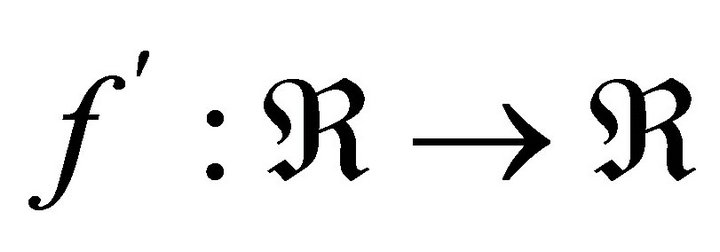 exists and is convex on
exists and is convex on .
.
Proof. See Pecaric et al. [7].
We are now in the position to state the key theorem of this paper.
Theorem 1. Let  be the value function stated in (2). Then for any
be the value function stated in (2). Then for any ,
,  is 3-convex.
is 3-convex.
Proof. Let 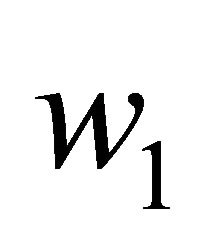 and
and  be some arbitrary number in
be some arbitrary number in  such that
such that . Then it suffices to show the following inequality:
. Then it suffices to show the following inequality:
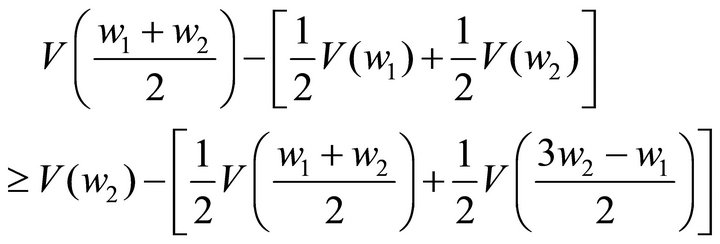
which is equivalent in showing that
 (7)
(7)
Let sequence  and
and  be the optimal consumption path given state
be the optimal consumption path given state 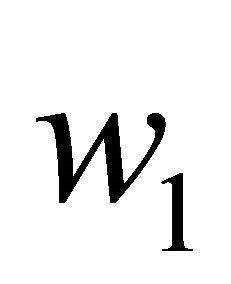 and
and , respectively. Now, define
, respectively. Now, define
 and
and 
Further, define
 and
and .
.
Then from Chmielewski and Manousiouthakis [6], the sequence
 (or
(or )
)
is feasible, but not necessarily equal to the optimal consumption path given the state  (or
(or ). Therefore,
). Therefore,
 and
and .
.
Then from the inequality (7), it follows that
 (8)
(8)
Rearranging the right-hand side of the inequality (8) and from the definition of the utility function, it follows that

Thus, This proves the theorem.
This proves the theorem. 
The concavity of the optimal consumption function follows naturally from Lemma 1 and Theorem 1.
Theorem 2. Let  be the optimal consumption function of the dynamic optimization problem (2). Then for any
be the optimal consumption function of the dynamic optimization problem (2). Then for any  in
in ,
,  is concave.
is concave.
Proof. Let  and
and  be some arbitrary number in
be some arbitrary number in  such that
such that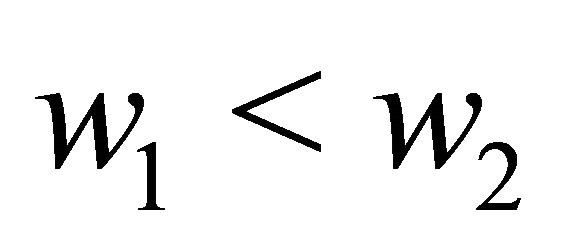 . Then it suffices to show,
. Then it suffices to show,
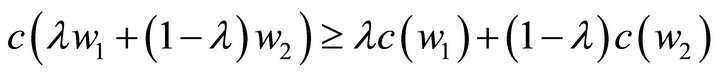
where . From Equation (5), this is equivalent in showing that
. From Equation (5), this is equivalent in showing that

Now from Theorem 1,  is 3-convex, which in turn implies that
is 3-convex, which in turn implies that  is convex from Lemma 1. This proves the theorem.
is convex from Lemma 1. This proves the theorem.
4. Concluding Remark
This paper showed, in the context of infinite horizon, how the presence of liquidity constraints generate a concavity in the consumption function, even when consumer is not prudent—i.e. preference is quadratic. In showing the concavity of the consumption function, we directly proved the 3-convexity (also known as Levinson’s inequality [3]) of the value function. This direct approach utilizing 3-convexity of the value function is convenient in characterizing the consumption function, especially in the infinite horizon context and can thought to be a complement, rather than a substitute, to Carroll and Kimball’s [2] backward induction approach for the finite horizon.
We thank Hiroshi Fujiki, Keiko Murata, Makoto Saito and, especially, Miles Kimball for their helpful comments and suggestions. This paper was written while the first author was at the Institute for Monetary and Economic Studies, Bank of Japan. The views expressed in this paper are those of the authors and do not necessarily reflect those of the Bank of Japan or the Institute for Monetary and Economic Studies.
REFERENCES
- A. Deaton, “Saving and Liquidity Constraints,” Econometrica, Vol. 59, No. 5, 1991, pp. 1221-1248. doi:10.2307/2938366
- C. D. Carroll and M. S. Kimball, “Liquidity Constraints and Precautionary Saving,” NBER Working Paper 8496, National Bureau of Economic Research, Inc., 2001.
- N. Levinson, “Generalization of an Inequality of Ky Fan,” Journal of Mathematical Analysis and Applications, 8, 1964, pp. 133-134. doi:10.1016/0022-247X(64)90089-7
- C. D. Carroll and M. S. Kimball, “On the Concavity of the Consumption Function,” Econometrica, Vol. 64, No. 4, 1996, pp. 981-992. doi:10.2307/2171853
- N. L. Stokey, R. E. Lucas Jr. and E. C. Prescott, “Recursive Methods in Economic Dynamics,” Harvard University Press, Cambridge, 1989.
- D. Chmielewski and V. Manousiouthakis, “On Constrained Infinite-time Linear Quadratic Optimal Control, Systems and Control Letters, Vol. 29, No. 3, 1996, pp. 121-129. doi:10.1016/S0167-6911(96)00057-6
- J. E. Pecaric, F. Proschan and Y. L. Tong, “Convex Functions, Partial Orderings, and Statistical Applications Academic Press, San Diego, 1992.
NOTES
1For the concavity of the consumption function generated by prudence, see Carroll and Kimball [4].
2Uncertainty in rate-of-return or labor income can be easily introduced in the model set-up, but will not alter the main implication. Indeed, since the very message of this paper is the concavity of consumption function under deterministic environment, introduction of uncertainty will only obscure the main point of this paper.
3We assume the regularity condition on discount rate to ensure the Contraction Mapping Theorem to hold. For more rigorous treatment on this issue, see for Stokey and Lucas [5]. Also, for the existence of converged value function under the case where control variables are constrained, see for instance Chmielewski and Manousiouthakis [6].
4It should be noted that when the value function is quadratic (as in the case when preference is quadratic and without liquidity constraints), the optimal consumption function will be linear. This can be easily seen from Equation (5).
5Or, in the continuous analouge,  is increasing in x.
is increasing in x.

