M. RABIU ET AL. 53
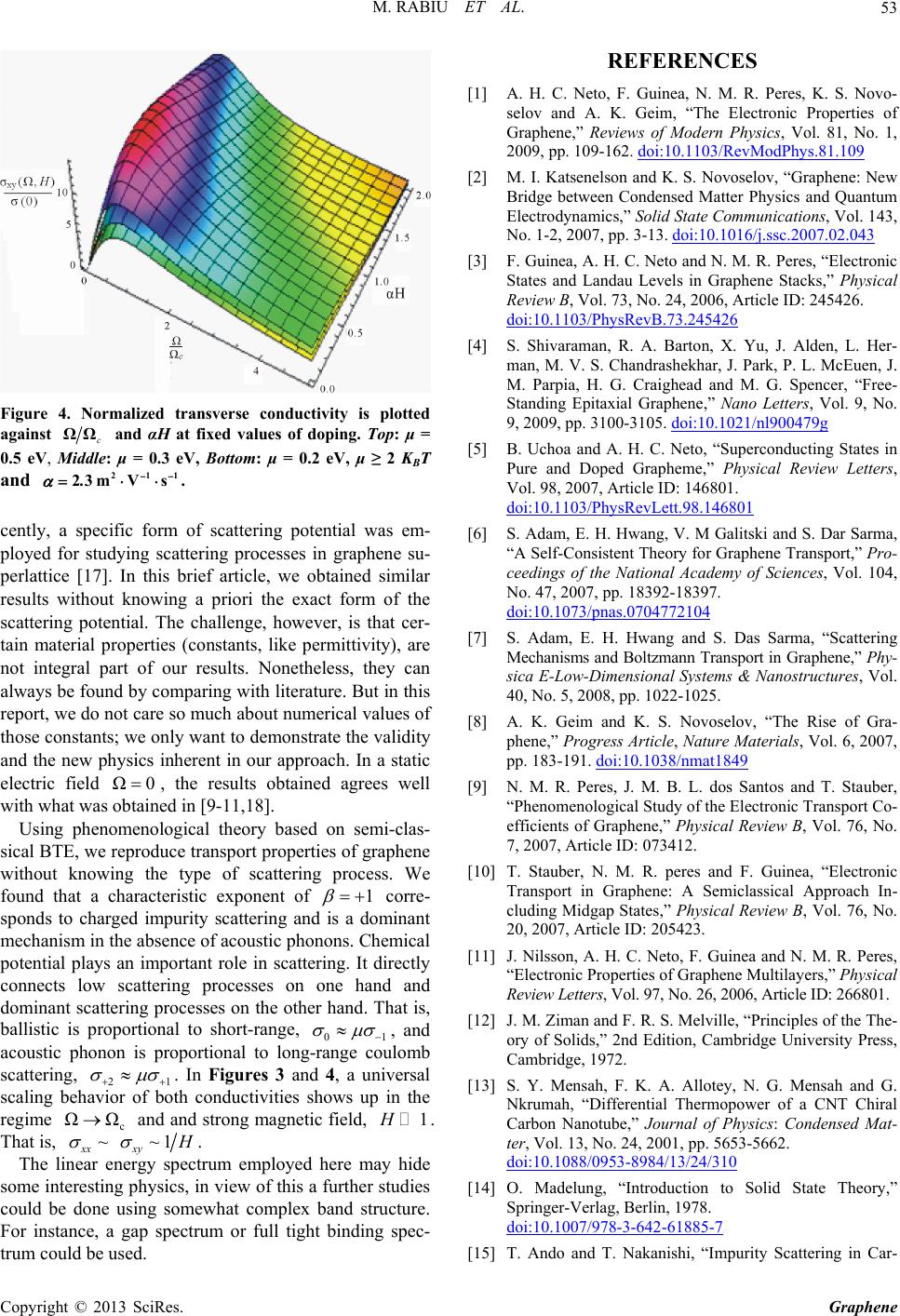
Figure 4. Normalized transverse conductivity is plotted
against c
ΩΩ and αH at fixed values of doping. Top: μ =
0.5 eV, Middle: μ = 0.3 eV, Bottom: μ = 0.2 eV, μ ≥ 2 KBT
and 211
23mVs.
.
cently, a specific form of scattering potential was em
ain
ased on semi-clas-
si
-
ployed for studying scattering processes in graphene su-
perlattice [17]. In this brief article, we obtained similar
results without knowing a priori the exact form of the
scattering potential. The challenge, however, is that cer-
tain material properties (constants, like permittivity), are
not integral part of our results. Nonetheless, they can
always be found by comparing with literature. But in this
report, we do not care so much about numerical values of
those constants; we only want to demonstrate the validity
and the new physics inherent in our approach. In a static
electric field Ω0, the results obtained agrees well
with what was obted in [9-11,18].
Using phenomenological theory b
cal BTE, we reproduce transport properties of graphene
without knowing the type of scattering process. We
found that a characteristic exponent of 1
corre-
sponds to charged impurity scattering and minant
mechanism in the absence of acoustic phonons. Chemical
potential plays an important role in scattering. It directly
connects low scattering processes on one hand and
dominant scattering processes on the other hand. That is,
ballistic is proportional to short-range, 01
is a do
, and
acoustic phonon is proportional to long-lomb
scattering, 21
range cou
. In Figures 3 and 4, a universal
scaling behth conductivities shows up in the
regime c
ΩΩ and and strong magnetic field, 1
avior of bo
.
That is, 1
xy ~H
xx ~
near ene
.
The litrurgy specm employ
so
trum could be used.
. Guinea, N. M. R. Peres, K. S. Novo-
selov and A. K. Geim, “The Electronic Properties of
Graphene,” Re, Vol. 81, No. 1,
2009, pp. 109-dPhys.81.109
ed yhere ma hide
me interesting physics, in view of this a further studies
could be done using somewhat complex band structure.
For instance, a gap spectrum or full tight binding spec-
REFERENCES
[1] A. H. C. Neto, F
views of Modern Physics
162. doi:10.1103/RevMo
[2] M. I. Katsenelson and K. S. Novoselov, “Graphene: New
Bridge between Condensed Matter Physics and Quantum
Electrodynamics,” Solid State Communications, Vol. 143,
No. 1-2, 2007, pp. 3-13. doi:10.1016/j.ssc.2007.02.043
[3] F. Guinea, A. H. C. Neto and N. M. R. Peres, “Electronic
States and Landau Levels in Graphene Stacks,” Physical
Review B, Vol. 73, No. 24, 2006, Article ID: 245426.
doi:10.1103/PhysRevB.73.245426
[4] S. Shivaraman, R. A. Barton, X. Yu, J. Alden, L. Her-
man, M. V. S. Chandrashekhar, J. Park, P. L. McEuen, J.
M. Parpia, H. G. Craighead and M. G. Spencer, “F
Standing Epitaxial Graphene,” Nan ree-
o Letters, Vol. 9, No.
9, 2009, pp. 3100-3105. doi:10.1021/nl900479g
[5] B. Uchoa and A. H. C. Neto, “Superconducting States in
Pure and Doped Grapheme,” Physical Review Letters,
Vol. 98, 2007, Article ID: 146801.
doi:10.1103/PhysRevLett.98.146801
[6] S. Adam, E. H. Hwang, V. M Galitski and S. Dar Sarma,
“A Self-Consistent Theory for Graphene Transport,” Pro-
ceedings of the National Academy of
No. 47, 2007, pp. 18392-18397.
Sciences, Vol. 104,
doi:10.1073/pnas.0704772104
[7] S. Adam, E. H. Hwang and S. Das Sarma, “Scattering
Mechanisms and Boltzmann Transport in Graphene,” Phy-
sica E-Low-Dimensional Systems
40, No. 5, 2008, pp. 1022-1025.
& Nanostructures, Vol.
[8] A. K. Geim and K. S. Novoselov, “The Rise of Gra-
phene,” Progress Article, Nature Materials, Vol. 6, 2007,
pp. 183-191. doi:10.1038/nmat1849
[9] N. M. R. Peres, J. M. B. L. dos Santos and T. Stauber,
“Phenomenological Study of the Electronic Transport Co-
efficients of Graphene,” Physical Review B, Vol. 76, No.
7, 2007, Article ID: 073412.
[10] T. Stauber, N. M. R. peres and F. Guinea, “Electronic
Transport in Graphene: A Semiclassical Approach In-
cluding Midgap States,” Physical Review B, Vol. 76, No.
20, 2007, Article ID: 205423.
[11] J. Nilsson, A. H. C. Neto, F. Guinea and N. M. R. Peres,
“Electronic Properties of Graphene Multilayers,” Physical
Review Letters, Vol. 97, No. 26, 2006, Article ID: 266801.
[12] J. M. Ziman and F. R. S. Melville, “Principles of the The-
ory of Solids,” 2nd Edition, Cambridge University Press,
Cambridge, 1972.
S. Y. Mensah, F. K. A. Allotey, N. G. Mensah and G.[13]
Nkrumah, “Differential Thermopower of a CNT Chiral
Carbon Nanotube,” Journal of Physics: Condensed Mat-
ter, Vol. 13, No. 24, 2001, pp. 5653-5662.
doi:10.1088/0953-8984/13/24/310
[14] O. Madelung, “Introduction to Solid State Theory,”
Springer-Verlag, Berlin, 1978.
doi:10.1007/978-3-642-61885-7
[15] T. Ando and T. Nakanishi, “Impurity Scattering in Car-
Copyright © 2013 SciRes. Graphene