Engineering, 2013, 5, 157-162
doi:10.4236/eng.2013.51b029 Published Online January 2013 (http://www.SciRP.org/journal/eng)
Differential Evolution Immunized An t Colony
Optimization Technique in Solving Economic Load
Dispatch Prob lem
N. A. Rahmat, I. Musirin
Universiti Te knologi M ARA, Mala ysia
Received 2013
Abstract
Since t he introduction of Ant Colony Optimization (ACO) technique in 1992, the algorithm starts to gain popularity due
to its attractive features. However, several shortcomings such as slow convergence and stagnation motivate many re-
searchers to stop further implementation of ACO. Therefore, in order to overcome these drawbacks, ACO is proposed
to be combined with Differential Evolution (DE) and cloning process. This paper presents Differential Evolution Im-
munized Ant Colony Optimization (DEIANT) technique in solving economic load dispatch problem. The combination
creates a new algorithm tha t will be termed as Di fferential Evolutio n Immunized Ant Co lony Optimizatio n (DEIANT).
DEIANT was utilized to optimize economic load dispatch problem. A comparison was made between DEIANT and
classical ACO to evaluate the performance of the new algorithm. In realizing the effectiveness of the proposed tech-
nique, IEEE 57-Bus Reliable Test System (RTS) has been used as the test specimen. Results obtained from the study
revealed that the proposed DEIANT has superior computation time.
Keywords: Ant C olony Optimization (ACO), Differential Evolution (DE), Differential Evolution Immunized Ant Colony Opti-
mization (DEIANT)
1. Introduction
In 1992, Marco Dorigo introduced a probabilistic algo-
rithm known as Ant Colony Optimization (ACO) tech-
nique. In his PhD thesis, he described that ACO resem-
bles the natural behavior of a colony of ant during their
random expedition to find the best path between their
nest and food source. The ant will deposit a chemical
trace known as pheromone. The pheromone will act as
the stimulant to attract more ant s to utilize on the same
path. An y l e s s -traveled paths will be for gotte n since the ir
pheromone traces has been evaporated. Marco Dorigo
empl oyed this behavior into his research to solve the
travelling salesmen problem (TSP) [1] . Since, ACO has
attracted many researchers to employ the algorithm into
their research. Mohd Rozeli Kalil et. al successfully im-
plements ACO to gain maximum loadability in voltage
control study [2]. Ashish Ahuja and Anil Pahwa [3]
stated in their research that ACO significantly minimized
the loss i n a distribution s ystem. Moreover, D. Nualhong
et. al utilizes ACO in his research to solve the unit co m-
mitment problems [4]. However, further research on the
algorithm indicates that ACO suffers from several short-
comings. H. B. Duan, et al stated in his research that
ACO may exper ience stagnation due to its positive feed-
back strategy. The researcher also highlighted that the
random selection strategy of ACO makes the algorithm
sluggish [5]. Another researcher claimed that ACO has
slow convergence rate [6-7].
Another attractive optimization technique is the Diffe-
rential Evolution (DE). DE was created by Storn and
Price in 1995 [8]. As a typical Evolutionary Algorithm
(EA), DE was used to sol ve stochastic , no n -differentiable,
non-linear, multi-dimensional and population-based op-
timization problem [9]. The algorithm was also used to
solve a Chebychev Polynomial Fitting Problem during
the First Inte rnati o na l Conte s t o n Evo l ut io nary Comp ute r
(1st ICE O) in Na goya. As a typi cal Evo lutio n Algo rith m,
DE comprises of mutation, crossover, and selection
process. In 1997, Storn and Price stated that DE is much
better than Simulated Annealing and Genetic Algorithm
[10]. As such, DE has become the candidate technique to
optimize Neural Network Learning, Radio Network de-
sign, multiprocessor synthesis and gas transmission net-
work design. Therefore, this paper presents Differential

N. A. RAHMAT, I. MUSIRI
158
Evolution Immunized Ant Colony Optimization
(DEIANT) technique in solving economic load dispatch
problem. The aim of the proposed technique is to alle-
viate the slow convergence, and stagnation experienced
in the traditional ACO through the application of DE.
The performance of DEIANT will be evaluated b y using
the algorithm to solve and optimize economic load dis-
patch problems. Performance evaluation of the proposed
DEIANT revealed that the proposed technique is supe-
rior than the traditional ACO in terms of achieving op-
timal solutio n and c omputation time.
2. Differential Evolution Immunized Ant
Colony Optimization Formulation
The capability to achieve fast convergence has been iden-
tified as the attractive feature of DE [10]. This feature
will be used to compensate the stagnation of ACO algo-
rithm. The modification of ACO algorithm will be focus-
ing o n the pheromone upda ting rule which is subject ed to
cloning, mutation, crossover, and selection process. Fig-
ure 1 depi cts the ove rall str ucture and proce sses of Diffe-
rential Evolution Immunized Ant Colony Optimization
(DEI ANT) algorithm. DEIANT is configured from the
combination of original ACO, combined with DE and
cloning process. ACO search agent will initialize random
tours and deposit pheromone layers. The algorithm will
update the pheromone level at each iteration. Cloning
process will increase the pheromone amount by generat-
ing the exact copies of the pheromone layer. To enhance
the pheromone layer, DE will mutate and crossover the
pheromone layer, thus increasing the diversity of the
pheromone. ACO will evaluate the fitness of the phero-
mone layer.
ACO
Cloning
process
DE
Ant colony deposit
pheromone layer
Increases pheromone
quantity
Mutation and
crossover process
enhance pheromone
diversity
DEIANT∑
Figure 1. Structural diagram of DEIA NT
2.1. Initialization
DEIANT consist of several classical ACO parameters.
Therefore, similar to ACO technique, the initial num-
ber of ant, nodes, pheromone decay parameter, α, and
the initial pheromone level, τ0 will be heuristically in-
itializ ed . The maxi mum distance travelled by each ant,
dmax, is subjected to a constraint in order to avoid large
computation time. dmax is obtained by calculating the
longest distance travelled by the ants. Each ant will tour
and select the next unvisited node until all nodes have
been visited.
2.2. Apply State Transition Rule
The next un visit ed no de is chosen according to the state
transition rule, s. Each node can only be visited once.
The ant that was positio ned at node(r) will go to the next
node(s).
[ ]
[ ]
[ ]
[ ]





⋅
⋅
=
∑
β
β
ητµε
ητ
)u.r()u,r(J
)s.r()s,r(
)s,r(P
)r(k
k
(1)
2.3. Apply Local Updating Rule
Altering the level of pheromone deposition is done dur-
ing the construction of solution. The amount of phero-
mone is either increased or decreased to vary the attrac-
tiveness of the route via the evaporation rate, ρ. Dorigo
stated that parameter ρ is needed to avoid the algorithm
converge pre-maturely. The parameter ρ act as a multip-
lier and is set between 0 to 1. In thi s rese arc h, t he e vapo-
ration rate is set to 0.7, meaning that at every iteration;
the pheromone will be reduced by 0.7.
2.4. Pheromone Cloning
The cloning process from Artificial Immune System is
implemented into DEIANT. The p heromo ne level will be
duplicated to increase pheromone population and diver-
sity. Figure 2 below depicts the cloning of the original
pheromone level.
Where υ represents the set of pheromone that will be
cloned, and ω represents the c loned pheromone set. Both
υ and ω can be written as υ = 1,…,V and ω = 1,…W,
respectively.
2.5. Pheromone Mutation
The pheromo ne mutation process is used to enhance the
pheromone layer over the visited node during ant
exploration. The Gaussian Distribution Equation was
utilized to mutate the pheromone level as in (2):
[ ]
υω
sr 
[ ]
12
sr 
[ ]
11
sr 
Figure 2 . Pheromone cloning process

N. A. RAHMAT, I. MUS IRI
159
( )







⋅−⋅+=
+max
i
minjmaxjj,ij,mi
f
f
XX,0NXX β
(2)
Where
j,mi
X
+: Pheromone mutation function
minj
X
: Smallest visited node
maxj
X
: Largest visited node
i
f
: Distance travelle d by ant
max
f : Longest distance tr a velled b y ant
2.6. Crossover
Crossover operation is implemented to emphasize the
diversification vector of the pheromone trail. The
mutated pheromone trail and the original one will merge
together by applying a binomial distribution known as
the crossover operation. In this algorithm, the original
and mutated p hero mone level will be resorte d withi n the
same matrix. The crossover matrix, Xgi is sorted in des-
cending order, as shown below:
Where n is the highest pheromone level for the tour,
and n-m is the lowes t phero m one level.
2.8 Selection
Trial pheromone trail, ρt is the product of the crossover
process. The algorithm will now select the required trail
accord ing to this rule:


≤
=otherwise ,
level, pheromone if ,
t
t
ρ
αρρ
ρ
Where α is the phero mone deca y parameter.
Basically, the selection process will specify the accepta-
ble condition to accept the pheromone level. The trail
with a higher pheromone leve l will b e selected. The trail
with fewer pheromone levels will be discarded.
2.9 Control Variable Calculation
The control variable x, is computed by applying the fol-
lowing equation:
Where:
d : distance for every ants tour
dmax : maximum distance for every ants tour
xmax : maximum of x
Variable x will become the multiplier to calculate the
objective function. In this research, variable x is multip-
lied with the co s t fu nctio n (7).
2.10 Global Updating Rule
After all ants have finished performing their random ex-
ploratio n, the best ant of the colony will be selected . The
best ant i s ca rryi ng t he d at a o f the b e s t to ur , and t hu s, t he
data will be stored. The following equation is applied to
update the pheromone level glo bally:
( )()( ) )s,r(.s,r1s,r τ∆ατατ +−←
(6)
The globally best tour will be selected as the first node of
the next iteration.
2.11 End Condition
The DEACO algorithm will halt the iteration when the
maximum number of iteration (tmax) has been reached
and all ants have completed their tours. If a b etter path is
discovered, it will be used as the reference. Only o ne an t
will find the optimal pa th.
3. Economic Load Dispatch Formulation
Economic load dispatch is the operation of determining
the optimal output that must be produced by the genera-
tion facilities to feasibly satisfy the load demand [12].
Therefore, the key objective of economic load dispatch is
to reduce the operati ng cost of e ach generating unit in the
power system. The operation cost can be calculated by
utilizing equation (7):
∑
=
Ng
i
ii
)P(F cost
(7)
Where Ng is the number of generating unit. Fi(Pi) is the
cost function, and Pi is the real power output of the unit I,
measured in MW. Fi(Pi) is usually approximated by a
quadratic function:
cPbPa)P(F ii
2
iiii ++=
(8)
max
max
x
d
d
x⋅=
(5)










−−
−
=
mn1n
1nn
Xgi



(3)
(4)

N. A. RAHMAT, I. MUSIRI
160
Where ai, bi, and ci are the cost coefficients of generator i.
The above equation is subjected to both the equality and
inequality constraints.
The system power loss can be calculated by using the
po wer flow equation below (19):
∑∑ ∑
N
i
N
j
N
i
ooioijijiL
BPBPBPP ++=
(9)
Where Bij, Boi, and Boo are the B-loss coefficient.
The cost function is given b y equa tion (26):
2
nnn
cPbPaC ++=
(10)
The followings are the generators’ operating costs for
IEEE 57-Bus System. These equations are derived from
equa tion (10):
2
111
P0070.0P0.7400C++=
2
222 P0095.0P0.10200C++=
2
333
P0090.0P5.8220C++=
2
666
P0090.0P0.11200C++=
2
888P0080.0P5.10240C++=
2
999
P0075.0P0.12200C++=
2
121212 P0068.0P0.10180C++=
(11)
Where C1, C2, C3, C6, C8, C9 and C12 are the oper ating cost
functi ons for ge nerato r 1, gene rator 2, ge nerator 3, gene-
rator 6, generator 8, generator 9, and generator 12 re-
spectively.
The total operating cost, CT can be formulated as:
12986321TCCCCCCCC ++++++=
(12)
The total operating cost is the objective function for this
research. The objective is to cut-down the total operating
cost, while preserving the system constraints within the
permissible limits. While minimizing the operating cost,
it was initially es ti mated that the power loss will be re-
duced as well. Power loss is the marginal difference be-
tween the power produced, and the power sold to the
consumer [13].
4. Results and Discussion
The DEIANT algorithm was developed by using
MATLAB. The algorithm was used to optimize eco-
nomic load dispatch problem. The research was con-
ducted on IEEE-57 bus system. The system contains
seven gene rating un its. The load was varied to assess the
performance of the proposed algorithm. The objectives
are to minimize the total generating cost, to reduce
transmission loss, and to reduce the computation time.
Comparisons were made between DEIANT and the
original ACO. T able 1 tabulates the si mulatio n results o f
classical ACO algorithm. Table 2 tabulate s the simula-
tion results of the newly developed DEIANT algorithm.
Note that the load, designated by Qd at Bus 10 was va-
ried between 0 to 25MVAR to see the performance of
DEIANT in solving economic load dispatch problem.
The comparison of DEIANT and classical ACO un-
doubtedly points out that the ne w algorithm successfully
outperforms the classical ACO. Varying the load gives
less impac t to the performance of DEIANT. For example,
when Qd is set to 20MVAR, DEIANT generates the total
operating cost of 41855 $/h. T he cost is economical than
the one calculated by classical ACO (41862 $/h), giving
a price drop of 0.0167%. If the load was set to 15MVAR,
the idea is the same; DEIANT only generates lower
power loss.
Table 1. Simulati o n results of classical ACO
Qd (MVAR) P1 (MW) P2 (MW) P3 (MW) P6 (M W) P8 (MW) P9 (MW) P12 (MW) Plos s (MW) Total Cost
($/h) T ime (s)
0 137.1095 89.8488 45.1114 75.8669 463.3333 100 358.7308 19.2007 4 1842 30.63371
5 138.5126 96.3783 45.3754 74.8029 458.1759 96.2979 360.593 19.336 41856 70.29794
10 138.4993 96.3443 45.3752 74.7286 458.1097 96.6145 360.495 19.3666 41858 52.4811
15 138.4077 96.3373 45.377 74.6806 458.05 48 96.9501 360.4142 19.4217 41860 67.40478
20 138.4437 96.2948 45.375 9 74.5882 457.9824 97.268 360.3066 19.4597 41862 34.64456
25 138.4127 96.2995 45.366 74.7954 457.87 48 97.4865 360.121 19.5559 41866 53.20833
Table 2. Simulation results of DEIANT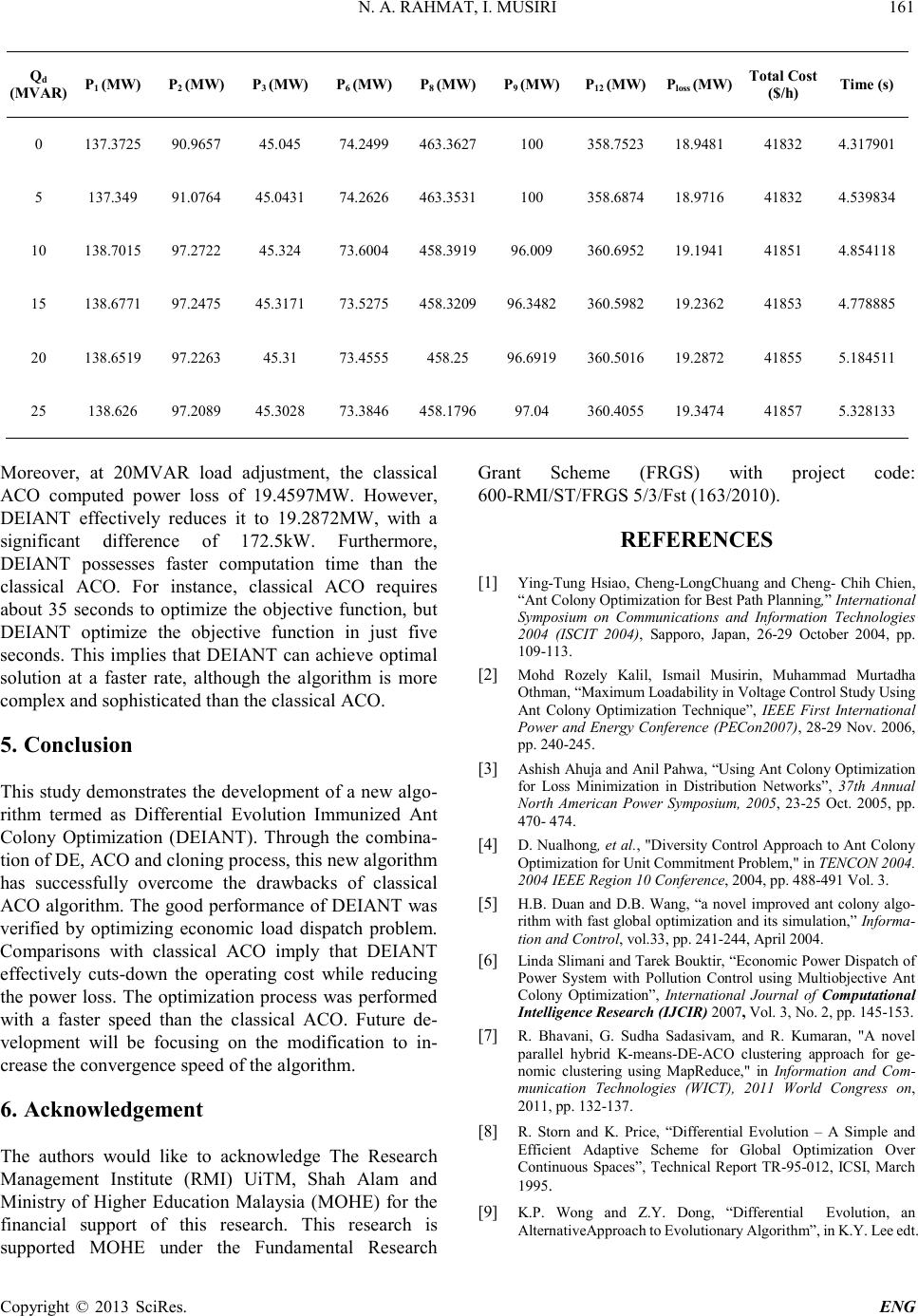

N. A. RAHMAT, I. MUS IRI
161
Qd
(MVAR) P1 (MW) P2 (MW) P3 (MW) P6 (MW) P8 (MW) P9 (MW) P12 (MW) Ploss (MW) Total Cost ($/h) Time ( s)
0 137.3725 90.9657 45.045 74.2499 463.3627 100 358.7523 18.9481 41832 4.317901
5 137.349 91.0764 45.0431 74.2626 463.3531 100 358.6874 1 8.9716 41832 4 .539834
10 138.7015 97.2722 45.324 73.6004 458.3919 96.009 360.6952 19.1941 41851 4.854118
15 138.6771 97.2475 45.3171 73.5275 458.3209 96.3482 360.5982 19.2362 41853 4.778885
20 138.6519 97.2263 45.31 73.4555 458.25 96.6919 360.5016 19.2872 41855 5.184511
25 138.626 97.2089 45.3028 7 3.3846 458.1796 97.04 360.4055 19.3474 41857 5.328133
Moreover, at 20MVAR load adjustment, the classical
ACO computed power loss of 19.4597MW. However,
DEIANT effectively reduces it to 19.2872MW, with a
significant difference of 172.5kW. Furthermore,
DEIANT possesses faster computation time than the
classical ACO. For instance, classical ACO requires
about 35 seconds to optimize the objective function, but
DEIANT optimize the objective function in just five
seconds. This implies that DE IANT can achieve optimal
solution at a faster rate, although the algorithm is more
complex and sophisticated than the cla ssic al A CO.
5. Conclusion
This study demonstrates the d evelop ment of a new al go-
rithm termed as Differential Evolution Immunized Ant
Colony Optimization (DEIANT). Through the combina-
tion of DE, ACO and cloning process, this new algor ith m
has successfully overcome the drawbacks of classical
ACO algorith m. T he good performance of DEIANT was
verified by optimizing economic load dispatch problem.
Comparisons with classical ACO imply that DEIANT
effectively cuts-down the operating cost while reducing
the power loss. The optimizatio n process was performed
with a faster speed than the classical ACO. Future de-
velopment will be focusing on the modification to in-
crease the convergence speed of the algorithm.
6. Acknowledgement
The authors would like to acknowledge The Research
Management Institute (RMI) UiTM, Shah Alam and
Ministry of Higher Education Malaysia (MOHE) for the
financial support of this research. This research is
supported MOHE under the Fundamental Research
Grant Scheme (FRGS) with project code:
600-RMI/ST/FRGS 5/3/Fst (163/2010).
REFERENCES
[1] Ying-Tung Hsiao, Cheng-LongChuang and Cheng- Chih Chien,
“Ant Colony Optimization for Best Path Planning,” International
Symposium on Communications and Information Technologies
2004 (ISCIT 2004), Sapporo, Japan, 26-29 October 2004, pp.
109-113.
[2] Mohd Rozely Kalil, Ismail Musirin, Muhammad Murtadha
Othman, “Maximum Loadability in Voltage Control Stud y Using
Ant Colony Optimization Technique”, IEEE First International
Power and Energy Conference (PECon2007), 28-29 Nov. 20 06,
pp. 240-245.
[3] Ashish Ahuja and Anil Pahwa, “Using Ant C olony Opti miza tion
for Loss Minimization in Distribution Networks”, 37th Annual
North American Power Symposium, 2005, 23-25 Oct. 2005, pp.
470- 474.
[4] D. Nualhong, et al., "Diversi ty Control App roach to Ant Colon y
Optimization for Unit Commitmen t Prob lem," in TENCO N 2 00 4.
2004 IEEE Region 10 Conference, 2004, pp. 488-491 Vol. 3.
[5] H.B. Duan and D.B. Wang, “a novel improved ant colony algo-
rithm with fast global optimization and its simulation,” Informa-
tion and Contro l, vol.33, pp. 241-244, April 2004.
[6] Lind a Slimani and Tarek Boukt ir, “Econom ic Power Dispa tch of
Power System with Pollution Control using Multiobjective Ant
Colony Optimization”, International Journal of Computational
Intelli gence Resear ch (I JCI R) 2007, Vol. 3, No. 2, pp. 1 45-153.
[7] R. Bhavani, G. Sudha Sadasivam, and R. Kumaran, "A novel
parallel hybrid K-means-DE-ACO clustering approach for ge-
nomic clustering using MapReduce," in Information and Com-
munication Technologies (WICT), 2011 World Congress on,
2011, pp. 132-137.
[8] R. Storn and K. Price, “Differential Evolution – A Simple and
Efficient Adaptive Scheme for Global Optimization Over
Continuous Spaces”, Technical Report TR-95-012, ICSI, March
1995.
[9] K.P. Wong and Z.Y. Dong, “Differential Evolution, an
AlternativeApproach to Evolutionary Algorithm”, in K.Y. Lee edt.

N. A. RAHMAT, I. MUSIRI
162
Intelligent Optimization and Control for Power Systems, IEEE
Publi shing , invited cha pter, No v. 200 5.
[10] Storn R., Price K.: ‘Differential Evolution – A Simple and Effi-
cient Adaptive Scheme For Global Optimization Over Continu-
ous Spa ce”, Jou rnal of Globa l Optimization, 1997.
[11] N. A. Rahmat, I. Musirin (2012). Differential Evolution Ant
Colony Opt im iza tion Tech niqu e (DE ACO) In S olvi n g Ec onom ic
Load Dispatch Problem. IEEE Internation Power Engineering
and Optimization.
[12] S. M. V. Pandian and K. Thanus hkodi, "Solvin g Economic Load
Dispatch Problem Considering Transmission Losses by Hybrid
EP-EPSO Algori thm for Solvin g Both S mooth and Non -Smooth
Cost Fu nction ," Intern ational Journal of Co mputer and Electric-
al Engineering, vol. 2, 2010
[13] M. Basu, “Artificial Immune System for Dynamic Economic
dispatch,” Electrical Power and Energy System, vol. 33, pp.
131-136, 7 June 2010