Fuzzy Time Series Forecasting Based On K-Means
Clustering
Zhiqiang Zhang
Department of Statistics
School of Economics
Xiamen University,
Xiamen, PR. China
e-mail: [e-mail]
Qiong Zhu
School of Mathematical Science
Xiamen University,
Xiamen, PR. China
e-mail:
Abstract—Many forecasting models based on the concepts of Fuzzy time series have been proposed in the past decades. These
models have been widely applied to various problem domains, especially in dealing with forecasting problems in which historical
data are linguistic values. In this paper, we present a new fuzzy time series forecasting model, which uses the historical data as the
universe of discourse and uses the K-means clustering algorithm to cluster the universe of discourse, then adjust the clusters into
intervals. The proposed method is applied for forecasting University enrollment of Alabama. It is shown that the proposed model
achieves a significant improvement in forecasting accuracy as compared to other fuzzy time series forecasting models.
Keywords fuzzy time series; fuzzy sets; K-means; enrollments
1. Introduction
A drawback of traditional forecasting methods is that they
can not deal with forecasting problems in which the historical
data are represented by linguistic values. Using fuzzy time
series to deal with forecasting problems can overcome this
drawback. Song and Chissom were the pioneers of studying
fuzzy time series models. The historical enrollment data of the
University of Alabama were first adopted by Song and
Chissom [1][2]. Because of its better performance in some
kinds of forecasting problems, many researchers have proposed
different fuzzy time series models in order to improve the
forecasting accuracy. Chen [3] presented a simplified method
of fuzzy time series forecasting of enrollments using the
arithmetic operations rather than complicated max-min
composition operations. Wang, Chen, and Lee [4] considered
to use high–order time variant fuzzy time series model to deal
with enrollment forecasting. Huarng [5] presented a heuristic
model for fuzzy time series using heuristic knowledge to
improve the forecast of enrollments. Jilani, Burney, Ardil [6]
used a triangular function to define the fuzzy sets. In this paper,
we present a new method to forecast enrollments based on k-
mean clustering techniques. First, we select the historical data
as the universe of discourse. Then we present the k-mean
clustering algorithm for clustering the data into different
lengths of intervals. Based on the new obtained intervals, we
can propose a new method to forecast the enrollment of the
university of Alabama. The proposed model is easy for
implementation and the forecasting is more accurate than the
other fuzzy time series methods.
The rest of this paper is organized as follows. In Section 2,
we briefly review the basic definitions of fuzzy time series
models. In Section 3, we present a new method for handing
forecasting problems based on k-means clustering techniques
through the experiments of forecasting of the university of
Alabama. In Section 4, we make a comparison of the proposed
forecasting model with existing methods. Finally, summary
and conclusions will be drawn in Section 5.
I. FUZZY TIME SERIES
In this section, we briefly review some basic concepts of
fuzzy time series proposed by Song and Chissom [1][2], where
the values of fuzzy time series are represented by fuzzy sets.
Let
U
be the universe of discourse, where
^`
n
uuuU ,,,
21
"
. A
fuzzy set A
in the universe of discourse
U
can be represented
by
n
nA AA
u
uf
u
uf
u
uf
A)(
)()(
2
2
1
1
"
(1)
Where
A
f
is the membership function of the fuzzy set
A
,
]1,0[: oUf
A
,
)(
iA
uf
denotes the grade of the membership
of i u in the fuzzy set A , and ni dd1 . Let
",2,1,0),( ttY
, is a subset of
R
, be the universe of
discourse on which fuzzy sets
)(tf
i
ˈ
...,3,2,1 i
are defined
and
)(tF
is the collection of
)(tf
i
, then
)(tF
is called fuzzy
time series on )(tY
. If there exists a fuzzy logical relationship
),1( ttR
such that
),,1()1()( ttRtFtF
where both
)(tF
and
)1( tF
are fuzzy sets and the symbol “  ”is the
max-min composition operator , then
)(tF
is called derived
by
)1( tF
, denoted by a fuzzy logical relationship shown as
follows:
)()1( tFtFo
. If
i
AtF )1(
and
j
AtF )(
,
where
i
A
and
j
A
are fuzzy sets, then the fuzzy logical
relationship between )1( tF
and
)(tF
can be represented by
Open Journal of Applied Sciences
Supplement：2012 world Congress on Engineering and Technology
100 Cop
y
ri
g
ht © 2012 SciRes.

ji
AA o
, where
i
A
and
j
A
are called current state and the
next state of the fuzzy logical relationship, respectively.
2. A New Method For Fuzzy Time Series
Forecasting
In this section, we present the stepwise procedure of the
proposed method for fuzzy time series forecasting based on
historical time series data and apply the proposed method to
forecast the enrollments of the University of Alabama. TABLE 1
shows the historical enrollments data of the University of
Alabama.
TABLE 1. HISTORICAL ENROLLMENTS OF UNIVERSITY OF
ALABAMA
YearActual enrollmentsYearActual enrollments
1971 13055 1982 15433
1972 13563 1983 15497
1973 13867 1984 15145
1974 14696 1985 15163
1975 15460 1986 15984
1976 15311 1987 16859
1977 15603 1988 18150
1978 15861 1989 18970
1979 16807 1990 19328
1980 16919 1991 19337
1981 16388 1992 18876
The proposed method and the experiment results are now
presented as follows:
Step 1: Apply the K-means clustering algorithm to partition
the historical time series data into 14 clusters and sort the data
in clusters in an ascending sequence, the results are as follows:
{13055},{13563},{13867},{14696},{15145,15163},{15311,1
5433,15460,15497},{15603},{15861},{15984},{16388},{168
07,16859,16919},{18150},{18876,18970},{19328,19337}.
Step 2: Calculate the cluster center
m
centercluster _
shown
in TABLE 2 of each cluster
m
cluster
as follows:
r
d
centercluster
r
jj
m
¦
1 _
(2)
Step 3: Adjust the clusters into intervals according to the
follow rules. Assume that
m
centercluster _ and
1
_
m
centercluster
are adjacent cluster centers, then the
upper bound
m
uBoundcluster _ of
m
cluster and the lower
bound
1
_
m
lBoundcluster
of
1m
cluster
shown in TABLE 2
can be calculated as follows:
2
__
_
1

mm
m
centerclustercentercluster
uBoundcluster
(3)
mm
uBoundclusterlBoundcluster __
1 
(4)
wher e
.1,2,1  km "
Because there is no previous
cluster before the first cluster and there is no next cluster after
the last cluster, the lower bound
1
_lBoundcluster
of the first
cluster and the upper bound
k
uBoundcluster _
of the last
cluster can be calculated as follows:
)__(
__
kk
kk
lBoundclustercentercluster
centerclusteruBoundcluster

)__(
__
11
11
centerclusteruBoundcluster
centerclusterlBoundcluster

After applying the procedure, we can get the following
intervals and calculate the middle value of the interval in
TABLE 2,
)13309,12801[
1 u
)13715,13309[
2
u
)14282,13715[
3
u
)14925,14282[
4
u
)15290,14925[
5
u )15514,15290[
6
u
)15732,15514[
7
u )15923,15732[
8
u
)16186,15923[
9
u )16625,16186[
10
u
)17506,16625[
11
u )18537,17506[
12
u
)19128,18537[
13
u
]19537,19128[
14
u
Step 4: Define each fuzzy set
i
X
based on the intervals and
the historical enrollments shown in TABLE 1, where fuzzy set
i
X
denotes a linguistic value of the enrollments represented
by a fuzzy set. As in [6], we use a triangular function to define
the fuzzy sets
i
X
.
Step 5: Defuzzify the fuzzy data using the forecasting formula
The support of National Social Science Fund Project (11BTJ001), MOE
Key Laboratory of Econometrics and Fujian Key Laboratory of Statistical
Sciences are gratefully acknowledged.
Cop
y
ri
g
ht © 2012 SciRes.101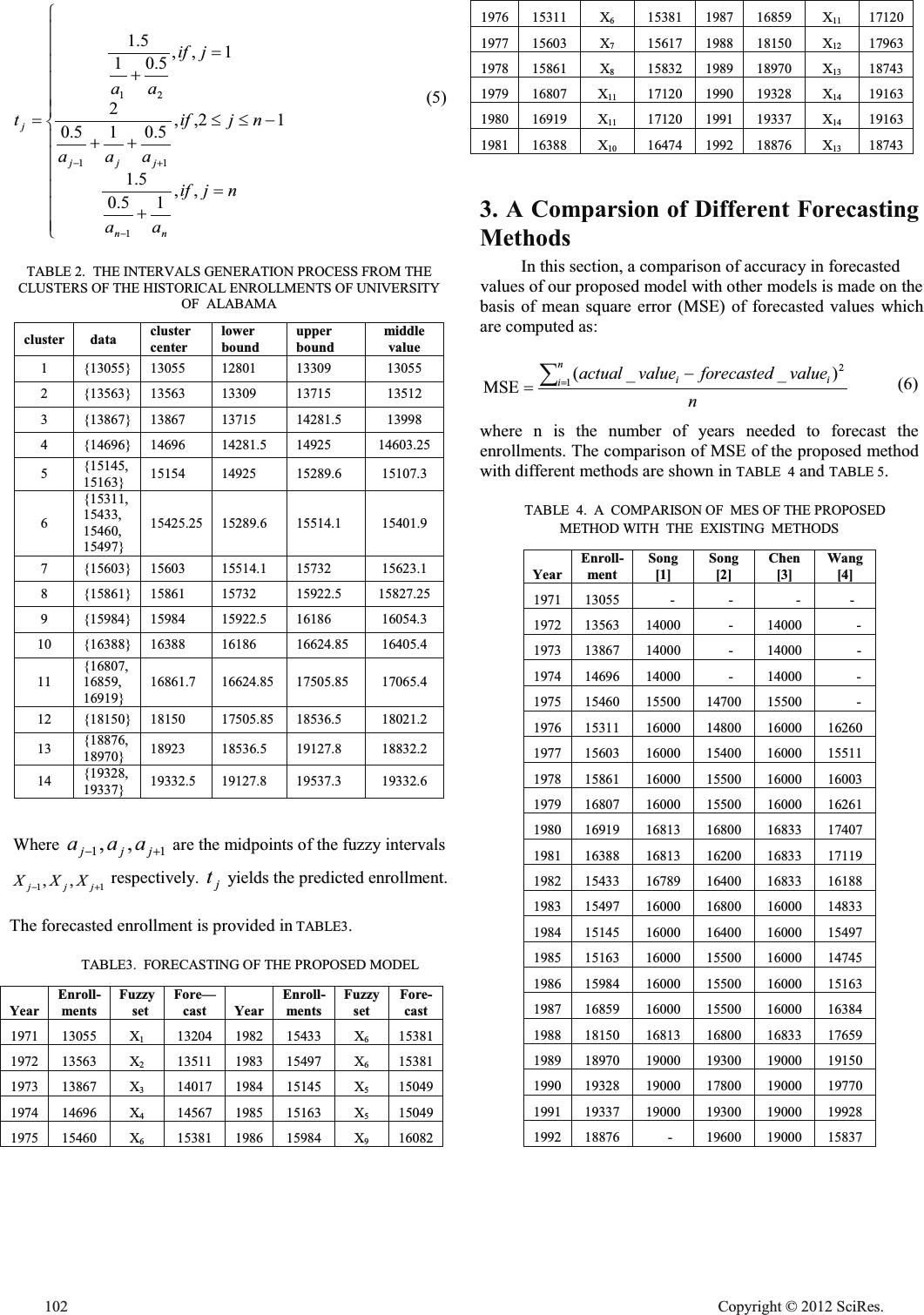

°
°
°
°
°
°
¯
°
°
°
°
°
°
®


dd




njif
aa
njif
aaa
jif
aa
t
nn
jjj
j
,,
15.0
5.1
12,,
5.015.0
2
1,,
5.01
5.1
1
11
21
(5)
TABLE 2. THE INTERVALS GENERATION PROCESS FROM THE
CLUSTERS OF THE HISTORICAL ENROLLMENTS OF UNIVERSITY
OF ALABAMA
cluster datacluster
center
lower
bound
upper
bound
middle
valu e
1 {13055} 13055 12801 13309 13055
2 {13563} 13563 13309 13715 13512
3 {13867} 13867 13715 14281.5 13998
4 {14696} 14696 14281.5 14925 14603.25
5 {15145,
15163} 15154 14925 15289.6 15107.3
6
{15311,
15433,
15460,
15497}
15425.25 15289.6 15514.1 15401.9
7 {15603} 15603 15514.1 15732 15623.1
8 {15861} 15861 15732 15922.5 15827.25
9 {15984} 15984 15922.5 16186 16054.3
10 {16388} 16388 16186 16624.85 16405.4
11
{16807,
16859,
16919}
16861.7 16624.85 17505.85 17065.4
12 {18150} 18150 17505.85 18536.5 18021.2
13 {18876,
18970} 18923 18536.5 19127.8 18832.2
14 {19328,
19337} 19332.5 19127.8 19537.3 19332.6
Where 11 ,,
 jjj
aaa are the midpoints of the fuzzy intervals
11
,,
jjj
XXX
respectively.
j
t yields the predicted enrollment.
The forecasted enrollment is provided in TABLE3.
TABLE3. FORECASTING OF THE PROPOSED MODEL
Year
Enroll-
ment s
Fuzzy
set
Fore—
cast Year
Enroll-
ment s
Fuzzy
set
Fore-
cast
1971 13055 X1 13204 1982 15433 X6 15381
1972 13563 X2 13511 1983 15497 X6 15381
1973 13867 X3 14017 1984 15145 X5 15049
1974 14696 X4 14567 1985 15163 X5 15049
1975 15460 X6 15381 1986 15984 X9 16082
1976 15311 X6 15381 1987 16859 X11 17120
1977 15603 X7 15617 1988 18150 X12 17963
1978 15861 X8 15832 1989 18970 X13 18743
1979 16807 X11 17120 1990 19328 X14 19163
1980 16919 X11 17120 1991 19337 X14 19163
1981 16388 X10 16474 1992 18876 X13 18743
3. A Comparsion of Different Forecasting
Methods
In this section, a comparison of accuracy in forecasted
values of our proposed model with other models is made on the
basis of mean square error (MSE) of forecasted values which
are computed as:
n
valueforecastedvalueactual
n
iii
¦

1
2
)__(
MSE
(6)
where n is the number of years needed to forecast the
enrollments. The comparison of MSE of the proposed method
with different methods are shown in TABLE 4 and TABLE 5.
TABLE 4. A COMPARISON OF MES OF THE PROPOSED
METHOD WITH THE EXISTING METHODS
Year
Enroll-
ment
Song
[1]
Song
[2]
Chen
[3]
Wan g
[4]
1971 13055 - - - -
1972 13563 14000 - 14000 -
1973 13867 14000 - 14000 -
1974 14696 14000 - 14000 -
1975 15460 15500 14700 15500 -
1976 15311 16000 14800 16000 16260
1977 15603 16000 15400 16000 15511
1978 15861 16000 15500 16000 16003
1979 16807 16000 15500 16000 16261
1980 16919 16813 16800 16833 17407
1981 16388 16813 16200 16833 17119
1982 15433 16789 16400 16833 16188
1983 15497 16000 16800 16000 14833
1984 15145 16000 16400 16000 15497
1985 15163 16000 15500 16000 14745
1986 15984 16000 15500 16000 15163
1987 16859 16000 15500 16000 16384
1988 18150 16813 16800 16833 17659
1989 18970 19000 19300 19000 19150
1990 19328 19000 17800 19000 19770
1991 19337 19000 19300 19000 19928
1992 18876 - 19600 19000 15837
102 Cop
y
ri
g
ht © 2012 SciRes.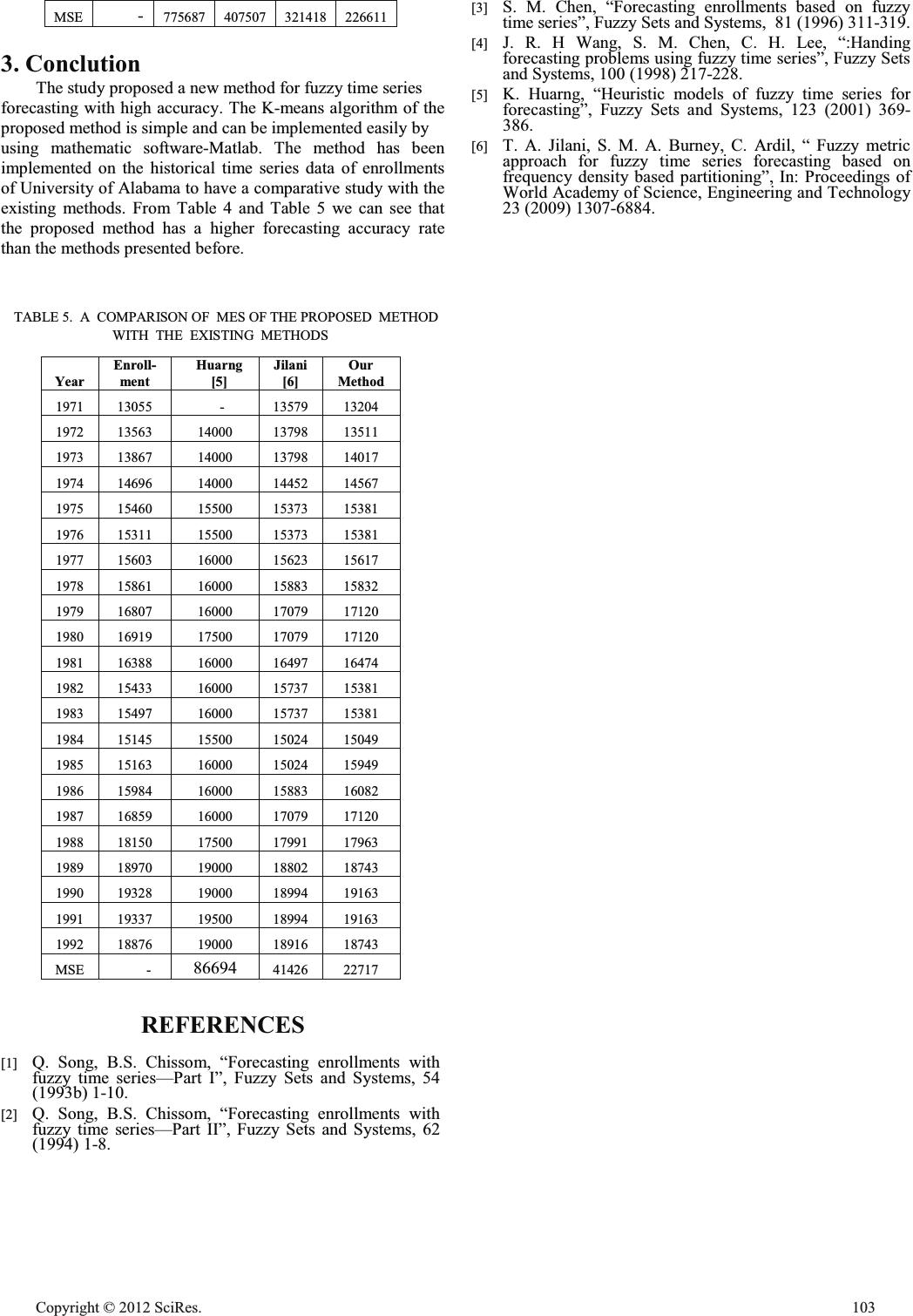

MSE - 775687 407507 321418 226611
3. Conclution
The study proposed a new method for fuzzy time series
forecasting with high accuracy. The K-means algorithm of the
proposed method is simple and can be implemented easily by
using mathematic software-Matlab. The method has been
implemented on the historical time series data of enrollments
of University of Alabama to have a comparative study with the
existing methods. From Table 4 and Table 5 we can see that
the proposed method has a higher forecasting accuracy rate
than the methods presented before.
TABLE 5. A COMPARISON OF MES OF THE PROPOSED METHOD
WITH THE EXISTING METHODS
Year
Enroll-
ment
Huarng
[5]
Jilani
[6]
Our
Method
1971 13055 - 13579 13204
1972 13563 14000 13798 13511
1973 13867 14000 13798 14017
1974 14696 14000 14452 14567
1975 15460 15500 15373 15381
1976 15311 15500 15373 15381
1977 15603 16000 15623 15617
1978 15861 16000 15883 15832
1979 16807 16000 17079 17120
1980 16919 17500 17079 17120
1981 16388 16000 16497 16474
1982 15433 16000 15737 15381
1983 15497 16000 15737 15381
1984 15145 15500 15024 15049
1985 15163 16000 15024 15949
1986 15984 16000 15883 16082
1987 16859 16000 17079 17120
1988 18150 17500 17991 17963
1989 18970 19000 18802 18743
1990 19328 19000 18994 19163
1991 19337 19500 18994 19163
1992 18876 19000 18916 18743
MSE -
86694 41426 22717
REFERENCES
[1] Q. Song, B.S. Chissom, “Forecasting enrollments with
fuzzy time series—Part I”, Fuzzy Sets and Systems, 54
(1993b) 1-10.
[2] Q. Song, B.S. Chissom, “Forecasting enrollments with
fuzzy time series—Part II”, Fuzzy Sets and Systems, 62
(1994) 1-8.
[3] S. M. Chen, “Forecasting enrollments based on fuzzy
time series”, Fuzzy Sets and Systems, 81 (1996) 311-319.
[4] J. R. H Wang, S. M. Chen, C. H. Lee, “:Handing
forecasting problems using fuzzy time series”, Fuzzy Sets
and Systems, 100 (1998) 217-228.
[5] K. Huarng, “Heuristic models of fuzzy time series for
forecasting”, Fuzzy Sets and Systems, 123 (2001) 369-
386.
[6] T. A. Jilani, S. M. A. Burney, C. Ardil, “ Fuzzy metric
approach for fuzzy time series forecasting based on
frequency density based partitioning”, In: Proceedings of
World Academy of Science, Engineering and Technology
23 (2009) 1307-6884.
Cop
y
ri
g
ht © 2012 SciRes.103