 Journal of Quantum Information Science, 2012, 2, 90-101 http://dx.doi.org/10.4236/jqis.2012.23015 Published Online September 2012 (http://www.SciRP.org/journal/jqis) A Comparative Study on Correlation Measures of Pure Bipartite States through Incomparability Amit Bhar1, Indrani Chattopadhyay2, Debasis Sarkar2 1Department of Mathematics, Jogesh Chandra Chaudhuri College, Kolkata, India 2Department of Applied Mathematic s, University of Calcut ta, Kolkata, India Email: bhar.amit@yahoo.com, icappmath@caluniv.ac.in, dsappmath@caluniv.ac.in Received July 20, 2012; revised July 30, 2012; accepted August 16, 2012 ABSTRACT The entanglement of a pure bipartite state is uniquely measured by the von-Neumann entropy of its reduced density matrices. Though it cannot specify all the non-local characteristics of pure entangled states. It was proven th at for every possible value of entanglement of a bipartite system, there exists an infinite number of equally entangled pure states, not comparable (satisfies Nielsen’s criteria) to each other. In this work, we investigate other correlation measures of pure bipartite states that are able to differentiate the quantum correlations of the states with entropy of entanglement. In Schmidt rank 3, we consider the whole set of states having same entanglement and compare how minutely such states can be distinguished by other correlation measures. Then for different values of entanglement we compare the sets of states belonging to the same entanglement and also investigate the graphs of different correlation measures. We extend our search to Schmidt rank 4 and 5 also. Keywords: LOCC; Entanglement; Incomparability 1. Introduction Non-local features of quantum mechanics distinguishes it from classical systems [1,2] and entanglement plays as a non-local resource to perform various computational tasks [3]. For this type of correlation between different subsystems of a composite system, we require a well defined process to quantify the amount of entanglement of a state. In asymptotic sens e, both th e quantities needed to prepare a pure bipartite state and distill pure entan- glement from it [4,5], are equal with the von-Neumann entropy of the reduced density matrices of the pure bi- partite state and is usually called as the entanglement of the state. Under stochastic local operations along with classical communications (in short, LOCC) this reversi- bility character and corresponding uniqueness of the measure of entanglement of pure bipartite systems are established [6]. It is found that the measures, not equiva- lent in asymptotic sense, with von-Neumann entropy of reduced density matrices for a pure system, are unable to impose consistent ordering on the set of all quantum sys- tems [7,8]. However the nature of evolution of composite systems in case of pure bipartite states under determinis- tic LOCC [9], are not very much clear to us. From the quantification procedures one may conclude that entan- glement is monotonic under LOCC [5,10,11]. Though it does not help us to identify a unique measure of entan- glement of pure bipartite systems. In case of mixed bi- partite systems the situation is more complex; e.g. the non-monotonicity of relative entropy of entanglement with negativity and concurrence [12]. We proceed here to find the existence of such ordering on different correla- tion measures for lower rank pure bipartite states. For this reason we critically observed the behaviour of pure bipartite systems under deterministic LOCC. The possi- bility of transforming one pure bipartite state to another is determined by the majorization relation between the Schmidt coefficients of the states specified by Nielsen’s criteria [13]. It immediately suggests us that it could not be always possible to transform a pure bipartite state to every other pure bipartite state having a lower amount of entanglement under deterministic LOCC. There are dif- ferent measures of entanglement, that are not equivalent with the von-Neumann entropy of reduced density ma- trices for pure bipartite states, depend directly on coeffi- cients of Schmidt decomposition of the state. Those measures could generate some ordering on the systems regarding possibility of its evolution under LOCC [14 ]. It is established that considering only single copy of the state, there are infinitely many measures generating dif- ferent ordering on the Schmidt form of the state [15]. This work is directed to characterize and compare the different correlation measures of entanglement under preservation of entanglement. We begin with the study C opyright © 2012 SciRes. JQIS  A. BHAR ET AL. 91 from 3 × 3 pure bipartite system, then 2 concentrating on 4 × 4 system ended with an example of 5 × 5 system. For higher and higher Schmidt rank, the behavior of lower rank systems indicate chaotic behavior. The brief outline of our work is as follows: in Section 2 we first recall the notion of entanglement of pure bipar- tite states shared between two distant parties. Then we discuss (Section 3) about the transformation of a pure bipartite system under deterministic LOCC governed by the majorization rule [16]. This is a nice ordering be- tween Schmidt vectors of the associated states. This pro- vides us the existence of pair of states, for which a higher entangled state could not be always transformed to a lower entangled one with certainty. In other words, their entanglement are not comparable (precisely, comparabil- ity means those states which would satisfy Nielsen’s cri- teria). This concept of incomparability (i.e. violets Niel- sen’s criteria, or in other words, the states are not con- vertible under deterministic LOCC) indicate a non-local feature not incorporated in the unique quantification scheme of entanglement for pure bipartite systems. Con- servation of entanglement under deterministic LOCC necessarily produced a class of states of same Schmidt rank, all mutually incomparable to each other (if not lo- cally unitarily connected). We mention here this class of states as equi-entangled. This work is mainly intended to study different measures of correlations in equi-entan- gled class. In Section 4, we recall the notions of such correlations measures [17] of pure states and some of their properties; e.g. Concurrence, Logarithmic Negativ- ity, Linear Entropy, Rényi Entropy, Concurrence Hier- archy, Maximum Fidelity, Robustness and some Dis- tance measures that depend only on the largest Schmidt coefficient of the state. In Section 5, we present all the graphs of the measures against the largest Schmidt coef- ficient and numerical tables for the correlation measures. We concentrate on studying pure bipartite system where the features of incomparability will be reflected neglect- ing the effect of entanglement via preservation of entan- glement under LOCC. In our whole work as we are mainly concerned about pure bipartite states, we will use occasionally the terms entanglement and entanglement of formation, as they have the same value and later is more operationally meaningful. In the appendix, we discuss about some other effects of incomparability. We prepare equal mixture of states from one equi-entangled class with maximally mixed states of same rank. The resulting mixed states sometimes preserve positivity under partial transpose operation, i.e. the states are PPT [18,19]. Whereas in equal mixture with some other states from the same class will generate NPT (negative under partial transposition) states. Also, we show that the o ptimal tele- portation fidelity, differ for different states of an equi- entangled class. 2. Pure State Entanglement The amount of entanglement of any pure bipartite state is uniquely described by the von-Neumann entropy of the reduced density matrices of the state and usually it is known as entropy of entanglement or simply entangle- ment of a pure bipartite state. It is established [20] that any measure of entanglement for a bipartite state (pure or mixed) is bounded by the limits defined by the two as- ymptotic measures, entanglement of formation and dis- tillable entanglement. For pure states both the measures coincide with the quantity entropy of entanglement. It is thus intuitive to con clude th at the non-local correlation of any pure bipartite state is uniquely characterized by the entropy of entanglement. However, recent observations in bipartite pure states compel us to rethink about the structure of state space with respect to the other measures of correlations [21]. To understand the nature of pure state entanglement we concentrate here on preservation of entanglement under LOCC. It has been found that for every possible amount of entanglement of non-maximally-entangled bipartite state of Schmidt rank d, there exists infinite number of equi-entangled pure bipartite states of same Schmidt rank [21]. This is quite understandable from the functional form of von-Neumann entropy, but what is much more physically significant that all such states are incomparable with each other. This is the key feature of investigating further the pure state entanglement and its evolution under local physical operations. We first recall the concept of comparability and in comparability of pure bipartite states. 3. Deterministic LOCC and Incomparability Any pure bipartite state of the joint Hilbert space =AB HH have the Schmidt representation: 1 =d iA B i ii (1) where A i and B i are orthonormal bases of the local Hilbert spaces A and respectively. The set of real numbers i , for , known as Schmidt coefficients of the state, are just the square-root of the eigenvalues of the reduced density matrices of the state, satisfying i =1 1,i ,2, ,id 0 and 1 d i 1 i . The number of Schmidt coefficients min dim,dim AB dHH known as the Schmidt rank of the pure bipartite state. The Schmidt coefficients remain invariant under any local unitary transformations on the pure bipartite state. Thus they are expected to serve well as ingredients of any good measure of entanglement. The notion of incomparability is a direct consequence Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. 92 of non-interconvertibility of pure bipartite states under deterministic LOCC. Given a pure bipartite state shared between two distant parties, suppose we want to convert it into another pure bipartite state under deterministic LOCC. The Schmid t vectors corresponding to the states , are 12 ,, n and 12 ,, m respectively(where 1ii0 0 for , =1,2, ,1in1jj nm for =1,2, ,1jm and =1 =1 =1= i ij j ). Then from Nielsen’s criterion [13], can be converted to with certainty under LOCC, denoted by , if and only if is majorized by (denoted by ) and describe as =1=1 , =1,2,, kk ii ii kd where we consider without loss of generality . Now, if the above criteria fails for at least one , then we usually denote it by ==dmn k , i.e. is not convertible to under deterministic LOCC. Though it may happen that . For some pair , whenever both and occur, then we denote it by and call , as a pair of incomparable states. For system there exists no incomparable pair of pure en tangled states. The explicit form of incomparability criteria for a pair of pure entangled states 22 , in , with Schmidt vectors 33 123 =, , and 12 =, 3 , is given by: whenever either of the following pair of relations 11223 1122 3 >>> >> > 3 3 (2) must hold. It is due to the fact that all incomparable pair of states in are strongly incomparable. The incomparability of pair of pure bipartite states could be used as a detector of many unphysical operations [22]. This aspect motivates us to investigate the effect of incomparability on different measures of correlations. In [23] it has been established that there is pair of in- comparable pure bipartite states for which entanglement of formation is not in general monotone with concurrence. Now, keeping in mind the criteria of deter- ministic local transformation of pure bipartite systems, one may ask about the effect on amount entanglement of the states involved. The consequence of Nielsen’s result is that if 33 of LOCC for this purpose. However, the mathematical form of von-Neumann entropy could not suggest us in either way. Interestingly it has been found that such states must be incomparable with each other [21]. Any pair of states, with different Schmidt vectors, from a class of equally entangled states cannot be deter- ministically converted to one another by LOCC. In other words, pure bipartite states with equal amount of en- tanglement, either they are locally unitarily connected or incomparable to each other. In the next section, we recall the notions of some correlation measures. 4. Correlation Measures Firstly, we consider some well-known correlation mea- sures, like, concurrence, linear entropy, logarithmic negativity, etc. Concurrence is one of the most important measure to quantify entanglement, functionally related to entangle- ment of formation [24] in systems (this is due to the wonderful invention of Wootters ). For any pure bipartite state 22 = in the Hilbert space AB H of two subsystems , B it is in general defined by 2 =21 A C , where A is the reduced density matrix of , after tracing out the subsystem . For mixed bipartite states, it is just the convex roof extension. The entanglement of formation for any state of the two-qubit system could be expressed as [25], B 2 11 =2 F C E where the function is defined as 22 =11 log log xx xx d . For higher dimen- sional pure bipartite state (say, ), concurrence is given by [26] d d2 <= =4 =21 ij i ij i C1 (3) which varies sm oothly from for product states to 0 21d d for maximally entangled pure states of Schmidt rank . d under LOCC with certainty, then EE where .E equals to the von-Neumann entropy of the reduced density matrices of the subsystems and usually known as the entropy of entanglement. Again, if someone search for what kind of deterministic LOCC, the amount of entanglement of the states could be preserved. All the local unitary operations preserve entanglement, so one must search for other kind Logarithmic Negativity is a computable measure of entanglement. It has functional relation with another important quantification scheme, known as negativity. Negativity is defined from the Peres-Horodecki criteria [18,19] by, 11 2 A T N (4) Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. 93 where 1 denote the trace norms of A T A T , partial transpose of the bipartite mixed state with respect to the subsystem A, which corresponds to the absolute value of the sum of the negative eigenvalues of A T and vanishes for separable states. For a pure state negativity is 2 11 2i i N . Now, Logarithmic Negativity, is defined by 22 1=2 log log A T LN N 1 It is an entanglement monotone[27], related to the PPT (positive under partial transposition) entanglement cost, PPT 2 = log EN 1 of the state , known as the cost of exact preparing under PPT preserving operations. For pure bipartite states this measure is calculated by d 2=1 =2 log i i LN (5) An interesting observation is that Negativity is a convex function [28] of the state, though Logarithmic Negativity is not. A series of correlation measures known as Rényi Entropy [29] or Alpha-Entropy ( S ), are proposed by generalizing the concept of von-Neumann entropy; 1 1 =ln 1 d i i S All the Rényi entropy measures (naturally excluding the von-Neumann Entropy function itself) are suitable to discriminate between any class of incomparable states with same entanglement. Here we only consider the Linear Entropy and for 2 S=3 i.e. . 3 Linear Entropy for the pure bipartite state in the form (1) is given by S 2 22 =log i i S (6) Giampaolo et al. [30] showed that for all non-maxi- mally entangled states of 3d system, there exists a range of values of linear entropy with same entangle- ment. Rényi entropy for =3 i.e. of the state (1) is computed by the fo rmula, 3 S 3 32 =log i i S (7) Now, we will provide notions of some other measure of correlations. Concurrence Hierarchy [31] is a series of correlation measures generalized from the concept of concurrence, in finite dimensional bipartite pure states. For a general bipartite pure state of rank d in the Schmidt form (1), the precise definition of the concur- rence hierarchy is given by: 12 112 ; 1,, kiii k iii d k Ck d (8) For 33 system, there is only one concurrence hierarchy for , i.e. =3k 31 =C23 . The Maximum fidelity for a pure state of the form (1), is given by, =1 max exp 2ln =d d i i F (9) The maximum fidelity is a convex function of the generalized entropy, max1 2 =exp H d where 12 is the Renyi entropy for 1 =2 . The correlation measure robustness of entanglement [32], denoted by R examines how much mixing can take place between an entangled state and any other state, so that the convex combination of these two states is separable. In the characterization of the state space in terms of entangled and separable states, we observe some interesting properties of this measure. Robustness R , is convex functio n of , i.e. for any two states 1 and 2 we have the following inequality 121 1ttR 2 1tRRt = . Robustness of entanglement remains unchanged under unitary transformation of state, i.e. L where RR UU U L is a local unitary transformation of the form 12 =UUU . Now for the pure state (1), we could define Robustness of entanglement as follows, 1 2 1 =exp2ln1 d i i R (10) Next we consider some of the distance measures of quantum correlationm [33], proposed from the view of measuring the distance of the state from its closest separable state [10]. For any two pure states and , the Fubini-Study distance is defined as, ,= FS dTr . It is bounded by, 0, 2 FS d . Fubini-Study distance is related to information theoretic measures of statistical distance between two probability distributions. From the concept of this distance between two states, a measure of correlation of a pure bipartite state is proposed as the minimum of Fubini-Study distance of the given state with all separable states and is obtained by the formula, max 1 = arccos=arccos min FS SEP FS d (11) Copyright © 2012 SciRes. JQIS 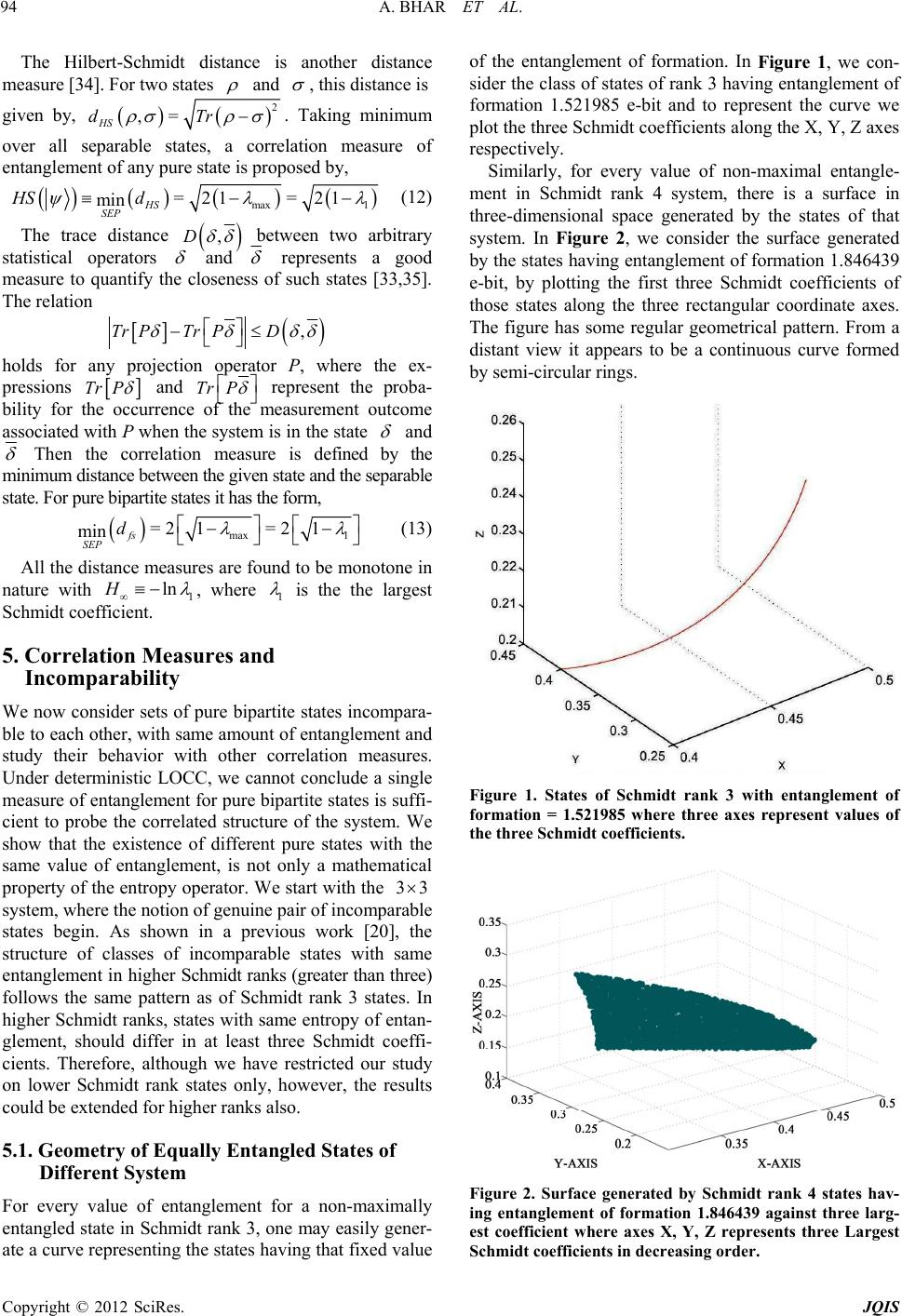 A. BHAR ET AL. 94 The Hilbert-Schmidt distance is another distance measure [34]. For two states and , this distance is given by, 2 ,= HS dTr . Taking minimum over all separable states, a correlation measure of entanglement of any pure state is proposed by, max 1 =21 =21 min HS SEP HS d (12) The trace distance ,D between two arbitrary statistical operators and represents a good measure to quantify the closeness of such states [33,35]. The relation ,Tr PTrPD holds for any projection operator P, where the ex- pressions Tr P and Tr P represent the proba- bility for the occurrence of the measurement outcome associated with P when the system is in the state and Then the correlation measure is defined by the minim um distanc e bet wee n the giv en stat e and the se para ble state. For pure bi partite states i t has the form , max 1 =2 1=2 1 min fs SEP d (13) All the distance measures are found to be monotone in nature with 1 lnH , where 1 is the the largest Schmidt coefficient. 5. Correlation Measures and Incomparability We now consider sets of pure bipartite states incompara- ble to each other, with same amount of entanglement and study their behavior with other correlation measures. Under deterministic LOCC, we cannot conclude a single measure of entanglement for pure bipartite states is suffi- cient to probe the correlated structure of the system. We show that the existence of different pure states with the same value of entanglement, is not only a mathematical property of the en tropy operator. We start with the 33 system, where the notion of genuine pair of incomparable states begin. As shown in a previous work [20], the structure of classes of incomparable states with same ent ang le ment i n h igh er Schmidt ranks (greater than three) follows the same pattern as of Schmidt rank 3 states. In higher Schmidt ranks, states with same entropy of entan- glement, should differ in at least three Schmidt coeffi- cients. Therefore, although we have restricted our study on lower Schmidt rank states only, however, the results could be extended for higher ranks also. 5.1. Geometry of Equally Entangled States of Different System For every value of entanglement for a non-maximally entangled state in Schmidt rank 3, one may easily gener- ate a curve representing the states having that fixed value of the entanglement of formation. In Figure 1, we con- sider the class of states of rank 3 having entanglement of formation 1.521985 e-bit and to represent the curve we plot the three Schmidt coefficients along the X, Y, Z axes respectively. Similarly, for every value of non-maximal entangle- ment in Schmidt rank 4 system, there is a surface in three-dimensional space generated by the states of that system. In Figure 2, we consider the surface generated by the states having entanglement of formation 1.846439 e-bit, by plotting the first three Schmidt coefficients of those states along the three rectangular coordinate axes. The figure has some regular geometrical pattern. From a distant view it appears to be a continuous curve formed by semi-circular rings. Figure 1. States of Schmidt rank 3 with entanglement of formation = 1.521985 where three axes represent values of the three Schmidt coefficients. Figure 2. Surface generated by Schmidt rank 4 states hav- ing entanglement of formation 1.846439 against three larg- est coefficient where axes X, Y, Z represents three Largest Schmidt coefficients in decre asing orde r. Copyright © 2012 SciRes. JQIS 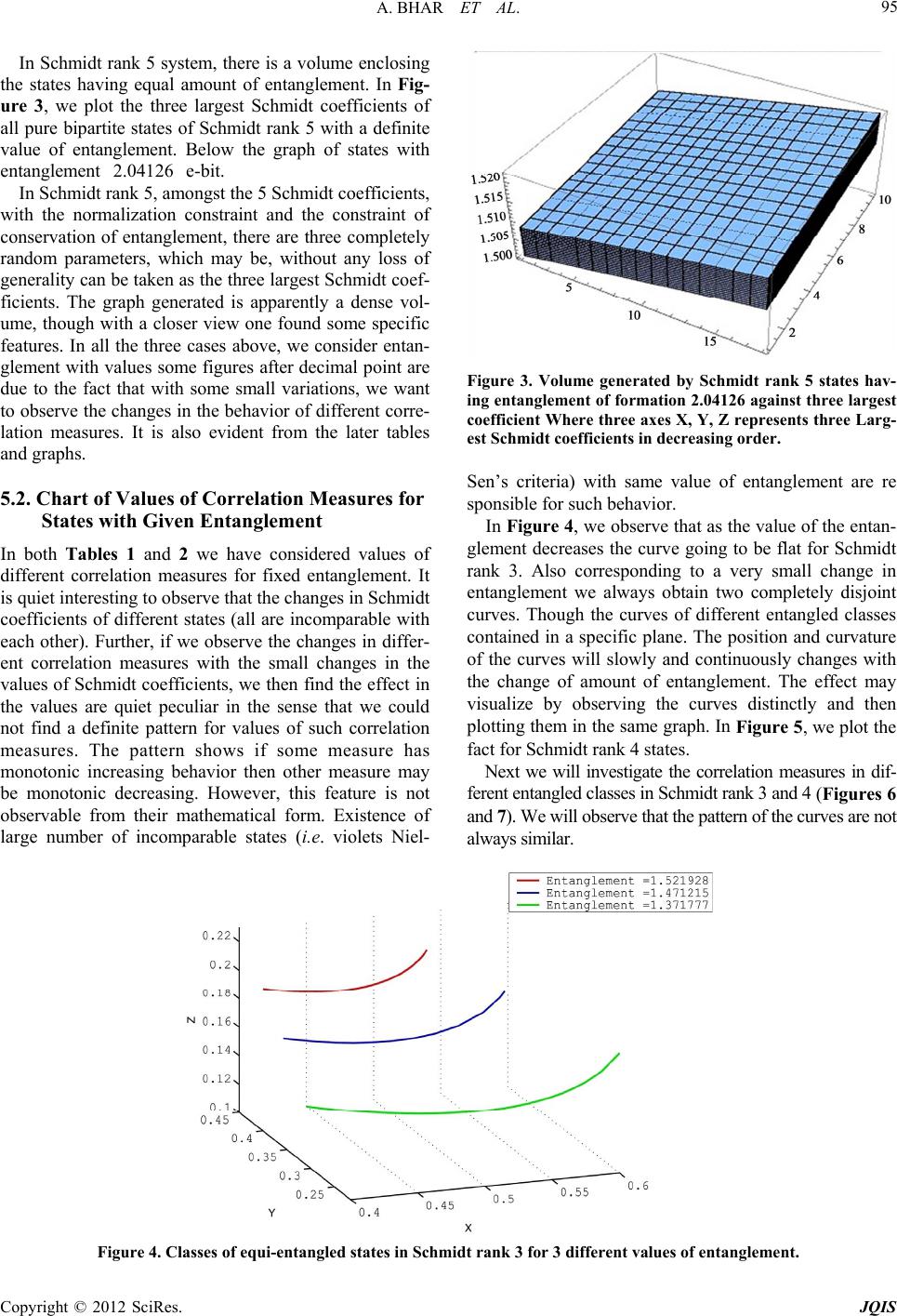 A. BHAR ET AL. Copyright © 2012 SciRes. JQIS 95 In Schmidt rank 5 system, there is a volume enclosing the states having equal amount of entanglement. In Fig- ure 3, we plot the three largest Schmidt coefficients of all pure bipartite states of Schmidt rank 5 with a definite value of entanglement. Below the graph of states with entanglement e-bit. 2.04126 In Schmidt rank 5, amongst the 5 Schmidt coefficients, with the normalization constraint and the constraint of conservation of entanglement, there are three completely random parameters, which may be, without any loss of generality can be taken as the three largest Schmidt coef- ficients. The graph generated is apparently a dense vol- ume, though with a closer view one found some specific features. In all the three cases above, we consider entan- glement with values some figures after decimal point are due to the fact that with some small variations, we want to observe the changes in the behavior of different corre- lation measures. It is also evident from the later tables and graphs. Figure 3. Volume generated by Schmidt rank 5 states hav- ing entanglement of formation 2.04126 against three largest coefficient Where three axes X, Y, Z represents three Larg- est Schmidt coefficients in decreasing order. Sen’s criteria) with same value of entanglement are re sponsible for such behavior. 5.2. Chart of Values of Correlation Measures for States with Given Entanglement In Figure 4, we observe that as the value of the entan- glement decreases the curve going to be flat for Schmidt rank 3. Also corresponding to a very small change in entanglement we always obtain two completely disjoint curves. Though the curves of different entangled classes contained in a specific plane. The position and curvature of the curves will slowly and continuously changes with the change of amount of entanglement. The effect may visualize by observing the curves distinctly and then plotting them in the same graph. In Figure 5, we plot the fact for Schmidt rank 4 states. In both Tables 1 and 2 we have considered values of different correlation measures for fixed entanglement. It is quiet interesting to observe that the changes in Schmidt coefficients of different states (all are incomparable with each other). Further, if we observe the changes in differ- ent correlation measures with the small changes in the values of Schmidt coefficients, we then find the effect in the values are quiet peculiar in the sense that we could not find a definite pattern for values of such correlation measures. The pattern shows if some measure has monotonic increasing behavior then other measure may be monotonic decreasing. However, this feature is not observable from their mathematical form. Existence of large number of incomparable states (i.e. violets Niel- Next we will investigate the correlation measures in dif- ferent e nta n gle d cl as ses in Schm idt rank 3 and 4 (Figures 6 and 7). We will observe that the patt ern of the curves are not always similar. Figure 4. Classes of equi-entangled states in Schmidt rank 3 for 3 different values of entanglement.  A. BHAR ET AL. 96 Table 1 . Entanglement of formation = 1.521928 e-bit. C CH LN 2 S 3 S (0.4, 0.4, 0.2) 1.13137085 0.032 1.5515754961.473931188 2.878321443 (0.402, 0.39798556, 0.20001444) (0.402, 0.39798547, 0.20001453) 1.131368833 1.131368864 0.032000349 0.032000356 1.551576754 1.551576924 1.473922043 1.473922185 2.878274014 2.878274353 (0.41, 0.3896249, 0.2003751) (0.41, 0.38962482, 0.20037518) 1.131319810 1.131319837 0.032009163 0.032009169 1.551609109 1.551609151 1.473699801 1.473699922 2.877111541 2.877111825 (0.415, 0.3841367, 0.2008633) (0.415, 0.3841362, 0.2008638) 1.13125411 1.131254272 0.032020971 0.032021009 1.551652439 1.551652699 1.473402018 1.473402753 2.875555225 2.875556928 (0.445, 0.345555, 0.209445) (0.445, 0.3455544,0.2094456) 1.130220805 1.130220949 0.032206771 0.032206808 1.552332793 1.552333037 1.468728979 1.468729631 2.851302596 2.851304012 (0.465, 0.30945889, 0.22554111) (0.465, 0.3094591, 0.2255409) 1.128841356 1.128841324 0.032455001 0.032454993 1.553237374 1.55323732 1.462520644 1.462520504 2.819567967 2.819567679 (0.473, 0.2867654, 0.2402346) (0.473, 0.2867657, 0.2402343) 1.128116964 1.128116939 0.032585429 0.032585423 1.553710668 1.553710624 1.459274145 1.459274034 2.803187775 2.803187552 MF R FS TR HS (0.4, 0.4, 0.2) 0.9771236171.9313708510.8860771241.54913338 1.095445115 (0.402, 0.39798556, 0.20001444) (0.402, 0.39798547,0.20001453) 0.977124469 0.977124502 1.931373407 1.931373506 0.8840367261.546609194 1.093617849 (0.41, 0.3896249, 0.2003751) (0.41, 0.38962482, 0.20037518) 0.977146382 0.977146411 1.931439146 1.931439233 0.8758913891.536229150 1.086278049 (0.415, 0.3841367, 0.2008633) (0.415, 0.3841362, 0.2008638) 0.977175731 0.977175907 1.931527193 1.931527721 0.8708129981.529705854 1.081665383 (0.445, 0.345555, 0.209445) (0.445, 0.3455544, 0.2094456) 0.977636661 0.977636827 1.932909983 1.932910481 0.8405096881.489966443 1.053565375 (0.465, 0.30945889, 0.22554111) (0.465, 0.3094591, 0.2255409) 0.978249840 0.978249803 1.934749520 1.934749409 0.8204268101.462873884 1.034408043 (0.473, 0.2867654, 0.2402346) (0.473, 0.2867657, 0.2402343) 0.978570819 0.978570789 1.935712457 1.935712367 0.8124113031451895313 1.026645021 Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. 97 Table 2. Entanglement = 1.4712154 e-bit. C CH LN 2 S 3 S (0.45, 0.39, 0.16) 1.113373253 0.02808 1.523115558 1.395169563 2.693947792 (0.46, 0.37804914,0.16195086) (0.46, 0.37804916, 0.16195084) 1.112879838 1.112879830 0.028163676 0.028163674 1.523457634 1.52345762 1.393086963 1.393086930 2.683948086 2.683948021 (0.47, 0.36532505, 0.16467495) (0.47, 0.36532508, 0.16467492) 1.112222791 1.112222780 0.028275146 0.028275143 1.523912199 1.523912178 1.390319798 1.390319752 2.670742795 2.670742882 (0.48, 0.35165453, 0.16834547) (0.48, 0.35165456, 0.16834544) 1.111394524 1.111394514 0.028415735 0.028415732 1.524483684 1.524483665 1.386841400 1.386841358 2.654273336 2.654273258 (0.49, 0.33676025, 0.17323975) (0.49, 0.33676030, 0.17323970) 1.110387791 1.110387776 0.028586728 0.028586724 1.525176047 1.525176018 1.382628248 1.382628187 2.634514394 2.634514282 | MF R FS TR HS (0.45, 0.39, 0.16) 0.958036852 1.874110556 0.835481874 1.483239679 1.048808848 (0.46, 0.37804914, 0.16195086) (0.46, 0.37804916, 0.16195084) 0.958264038 0.958264029 1.874792114 1.874792087 0.825440953 1.469693846 1.039230485 (0.47, 0.36532505, 0.16467495) (0.47, 0.36532508, 0.16467492) 0.958566002 0.958566016 1.875698006 1.875698048 0.815416193 1.456021978 1.029563014 (0.48, 0.35165453, 0.16834547) (0.48, 0.35165456, 0.16834544) 0.958945801 0.958945789 1.876837403 1.876837367 0.805403501 1.442220510 1.019803903 (0.49, 0.33676025, 0.17323975) (0.49, 0.33676030, 0.17323970) 0.959406119 0.959406100 1.878218357 1.8782183 0.795398830 1.428285686 1.009950494 0.65 Figure 5. Surface generated by equi-entangled states for different values of entangled states of Schmidt rank 4 where axes X, Y represents largest two Schmidt coefficients. Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. 98 Figure 6. Graphs of different correlation measures of equi-entangled states in Schmidt rank 3. Figure 7. Graphs of different correlation measures of equi-entangled state with entanglement of formation 2.04126 in Schmidt rank 4 considering three largest Schmidt coefficients. Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. Copyright © 2012 SciRes. JQIS 99 6. Observations The behavior of different correlation measures observed by plotting curves and by providing numerical figures. The nature of the curves show non-monotonic behavior of the measures in general with respect to the entangle- ment, e.g. concurrence [23]. This is observed due to only incomparability of a large number of states with same entanglement. For comparable states it would not be pos- sible to observe such behavior. This feature of state spaces has some other consequences, e.g. the behavior under partial transposition of mixtures of incomparable states from equi-entangled class with the maximally mixed state. We discuss this feature as distinguishing factor of the states belonging to any equi-entangled class in appendix. In conclusion, the work is intended to find the differ- ences by some known correlation measures of pure states through incomparability. As the Schmidt rank increases gradually only the measures depending on Schmidt coef- ficients would be able to differentiate the states of equal entanglement but incomparable with each other. For Schmidt rank 4 system, the behavior of the measures like, Concurrence, Linear Entropy and Rényi Entropy are similar in nature irrespective of some phase differences. Whereas the behavior of the measures like, Logarithmic Negativity, Concurrence Hierarchy, Maximum Fidelity and Robustness are quite opposite to that of the previous measures. Distance measures depending only on the largest Schmidt coefficient generate a straight line only indicating the variation of the largest Schmidt coefficient for preservation of entanglement under LOCC. The measure showing the largest variation for a fixed value of entanglement, for all most all values of entanglement in rank 4 system, is Concurrence Hierarchy and the next largest variation of values for constant entanglement is seen in the Rényi entropy for =3 . With the increase of entanglement, curvature of the surface as well as the area traced out by the states of an equi-entangled class will gradually shrinking down and tends to a line parallel to the X-axis, from a curved surface. REFERENCES [1] J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics, Vol. 1, No. 3, 1964, pp. 195-200. [2] C. H. Bennett and G. Brassard, “Quantum Cryptography: Public Key Distribution and Coin Tossing,”Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, 10-12 December 1984, pp.175-179. [3] C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres and W. K. Wootters, “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky- Rosen Channels,” Physical Review Letters, Vol. 70, No. 13, 1993, p. 1895. doi:10.1103/PhysRevLett.70.1895 [4] C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J. A. Smolin and W. K. Wootters, “Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels,” Physical Review Letters, Vol. 76, No. 5, 1996, pp. 722-755. doi:10.1103/PhysRevLett.76.722 [5] C. H. Bennett, H. J. Bernstein, S. Popescu and B. Schumacher, “Concentrating Partial Entanglement by Local Operations,” Physical Review A, Vol. 53, No. 4, 1996, pp. 2046-2052. doi:10.1103/PhysRevA.53.2046 [6] S. Popescu and D. Rohrlich, “Thermodynamics and the Measure of Entanglement,” Physical Review A (R), Vol. 56, No. 5, 1997, pp. 3319-3322. [7] S. Virmani and M. B. Plenio, “Ordering States with En- tanglement Measures,” Physical Revi ew Letters, Vol. 268, No. 1-2, 2000, pp. 31-34. doi:10.1016/S0375-9601(00)00157-2 [8] F. Verstraete, K. Audenaert, J. Dehaene and B. D. Moor, “A Comparison of the Entanglement Measures Negativity and Concurrence,” Journal of Physics A: Mathematical and General, Vol. 34, No. 47, 2001, p. 10327. doi:10.1088/0305-4470/34/47/329 [9] H. K. Lo and S. Popescu, “Concentrating Entanglement by Local Actions: Beyond Mean Values,” Physical Re- view A, Vol. 63, No. 2, 2001. doi:10.1103/PhysRevA.63.022301 [10] V. Vedral and M. B. Plenio, “Entanglement Measures and Purification Procedures,” Physical Review A, Vol. 57, No. 3, 1998, pp. 1619-1633. doi:10.1103/PhysRevA.57.1619 [11] V. Vedral, M. B. Plenio, M. A. Rippin and P. L. Night, “Quantifying Entanglement,” Physical Review Letters, Vol. 78, No. 12, 1997, p. 2275. doi:10.1103/PhysRevLett.78.2275 [12] A. Miranowicz and A. Grudka, “Ordering Two-Qubit States with Concurrence and Negativity,” Physical Re- view A, Vol. 70, No. 3, 2004, Article ID: 032326. doi:10.1103/PhysRevA.70.032326 [13] M. A. Nielsen, “Conditions for a Class of Entanglement Transformations,” Physical Review Letters, Vol. 83, No. 2, 1999, pp. 436-439. doi:10.1103/PhysRevLett.83.436 [14] K. Zyczkowski, “Volume of the Set of Separable States II,” Physical Review A, Vol. 60, No. 5, 1999, pp. 3496- 3507. doi:10.1103/PhysRevA.60.3496 [15] G. Vidal, “Entanglement Monotones,” Journal of Modern Optics, Vol. 47, No. 2-3, 2000, pp. 355-376. [16] M. A. Nielsen, “Lecture Notes,” Department of Physics, Univesity of Queensland, Queensland, 2002. [17] M. B. Plenio and S. Virmani, “An Introduction to Entan- glement Measures,” Quantum Information & Computa- tion, Vol. 7, No. 1, 2007, pp. 1-51. [18] A. Peres, “Seperability Criteria for Density Matrices,” Physical Review Letters, Vol. 77, No. 8, 1996, pp. 1413- 1415. doi:10.1103/PhysRevLett.77.1413 [19] M. Horodecki, P. Horodecki and R. Horodecki, “Separa- bility of Mixed States: Necessary and Sufficient Condi- tions,” Physical Review A, Vol. 223, No. 1-2, 1996, pp.  A. BHAR ET AL. 100 1-8. doi:10.1103/PhysRevLett.84.2014 [20] M. Horodecki, P. Horodecki and R. Horodecki, “Limits for Entanglement Measures,” Physical Review Letters, Vol. 84, No. 9, 2000, pp. 2014-2017. doi:10.1103/PhysRevLett.84.2014 [21] I. Chattopadhyay and D. Sarkar, “Character of Locally Inequivalent Classes of States and Entropy of Entangle- ment,” Physical Review A (R), Vol. 77, No. 5, 2008, Arti- cle ID: 050305. [22] I. Chattopadhyay and D. Sarkar, “General Classes of Impossible Operations through the Existence of Incom- parable states,” Quantum Information and Computation, Vol. 7, No. 4, 2007, pp. 392-400. doi:10.1103/PhysRevA.73.044303 [23] I. Chattopadhyay and D. Sarkar, “Entanglement of For- mation Is Non-Monotonic with Concurrence: A Simple Proof,” Quantum Information Processing, Vol. 7, No. 6, 2008, pp. 243-249. doi:10.1007/s11128-008-0085-6 [24] W. K. Wootters, “Entanglement of Formation of an Arbi- trary State of Two Qubits” Physical Review Letters, Vol. 80, No. 10, 1998, pp. 2245-2248. doi:10.1103/PhysRevLett.80.2245 [25] W. K. Wootters, “Entanglement of Formation and Con- currence,” Quantum Information & Computation, Vol. 1, No. 1, 2001, pp. 27-44. [26] K. Chen, S. Albeverio and S. M. Fei, “Concurrence of Arbitrary Dimensional Bipartite Quantum States,” Phy- sical Review Letters, Vol. 95, No. 4, 2005, Article ID: 040504. doi:10.1103/PhysRevLett.95.040504 [27] M. B. Plenio, “Logarithmic Negativity: A Full Entangle- ment Monotone That Is Not Convex,” Physical Review Letters, Vol. 95, No. 9, 2005, Article ID: 090503. doi:10.1103/PhysRevLett.95.090503 [28] G. Vidal and R. F. Werner, “Computable Measure of Entanglement,” Physical Review A, Vol. 65, No. 3, 2002, Article ID: 032314. doi:10.1103/PhysRevA.65.032314 [29] A. Rényi, “On the Notion of Entropy and Its Role in Probability Theory,” Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, Berkeley, Vol. 1, 1961, pp. 547-561. [30] S. M. Giampaolo and F. Elluminati, “Characterization of Separability and Entanglement in (2 × D)- and (3 × D)-Dimensional Systems by Single-Qubit and Single- Qutrit Unitary Transformations,” Physical Review A, Vol. 76, No. 4, 2007, Article ID: 042301. doi:10.1103/PhysRevA.76.042301 [31] H. Fan, K. Matsumoto and H. Imai, “Quantify Entangle- ment by Concurrence Hierarchy,” Journal of Physics A: Mathematical and General, Vol. 36, No. 14, 2003, p. 4407. doi:10.1088/0305-4470/36/14/316 [32] G. Vidal and R. Tarrach, “Robustness of Entanglement,” Physical Review A, Vol. 59, No. 1, 1999, pp. 141-155. doi:10.1103/PhysRevA.59.141 [33] K. Zyczkowski and I. Bengtsson, “Relativity of Pure States Entanglement,” Annals of Physics, Vol. 295, No. 2, 2002, pp. 115-135. doi:10.1006/aphy.2001.6201 [34] C. Writte and M. Trucks, “A New Entanglement Measure Induced by the Hilbert-Schmidt Norms,” Physics Letters A, Vol. 14, No. 1-2, 1999, pp.14-20. [35] G. Vidal, D. Jonathan and M. A. Nielsen, “Approximate Transformations and Robust Manipulation of Bipartite Pure-State Entanglement,” Physical Review A, Vol. 62, No. 1, 2000, Article ID: 012304. doi:10.1103/PhysRevA.62.012304 Copyright © 2012 SciRes. JQIS  A. BHAR ET AL. 101 Appendix Behavior of Mixture with Maximally Mixed State: Our observation is the signature of partial transpose on the mixture of states from a class of equally entangled states with the maximally mixed state through the PPT (positive under partial transpose) criteria [17,24]. Sup- pose 12 ,,, d be the Schmidt vector in decreas- ing order of the pure bipartite state of dd sys- tem. We prepare the mixture 2 1Ip dp for each state . Taking partial transpose over the subsystem B of the state, we find eigenvalues of the transpose matrix as, 2 1 ; =1,2,,d i pi dp and 2 1 ; =1,2,,1 ; =1,2,, ij pidjii dp d. Therefore, all the eigenvalues are non-negative when- ever, 2 < < < 12 1 {} min {1} 0 min {} max 1 ij ij ij ij ij ij p dp p p p Let be any pure bipartite state of system, having same entanglement but not local unitary equiva- lent with dd , i.e. both the states , are incom- parable with each other. Let the Schmidt vector in de- creasing order of be 12 ,,, d . When 12 12 , choosing the value of as p 12 12 11 <p we find is a PPT state and the state is NPT (negative under partial transpose). So for any pair of in- comparable states with same amount of entanglement if the product of two largest Schmidt coefficients are not equal, then we could always prepare equi-mixture of the two pure states with maximally mixed state in the same dimension( 2 1dd d ), such that one is PPT and another is a NPT state. The above feature undoubtedly probe the differences exist in different states of equi-entangled states, but not reflected by the unique quantification scheme for pure bipartite states through the von-Neu- mann entropy of the red uce d density mat ri c es. 0 1 (14) Copyright © 2012 SciRes. JQIS
|