Datum Definition in the Long Range Instantaneous RTK GPS Network Solution

Paper Menu >>

Journal Menu >>

Journal of Global Positioning Systems (2003)

Vol. 2, No. 2: 100-108

Datum Definition in the Long Range Instantaneous RTK GPS

Network Solution

Israel Kashani1,2, Pawel Wielgosz1,3, Dorota Grejner-Brzezinska1

1 The Ohio State University, CEEGS, 470 Hitchcock Hall, 2070 Neil Avenue, Columbus, OH 43210-1275

e-mail: kashani.1@osu.edu, tel.: 614-292-0169, fax: 614-292-2957

2 Technion - Israel Institute of Technology

3 University of Warmia and Mazury in Olsztyn, Poland

Received: 17 October 2003 / 16 December 2003

Abstract. This paper presents the multiple reference

station approach to wide area (and regional)

instantaneous RTK GPS, implemented in the MPGPSTM

(Multi Purpose GPS Processing Software) software,

developed at the Ohio State University. A weighted free-

net approach (WFN) was applied in the instantaneous

RTK software module, which enabled optimal estimation

of the rover coordinates, properly reflecting the

accuracies of the observations and the coordinates of the

CORS stations. The effect of using the distance-

dependent weighting scheme in the WFN approach on

the final rover solution is analyzed. The influence of the

different weights was studied by introducing the

distance-dependent weights as a function of the CORS

station separation L to the rover (1/L2). The results show

that almost 100% of the differences between the

computed horizontal rover coordinates and the known

reference coordinates are below a decimeter, and 95% of

the differences in the vertical coordinate are below 20

cm, when using the suggested approach. In addition, the

accuracy analysis of two other solutions, with different

datum definition (minimum constraint and over-

constrained), is presented. This analysis verifies the

suitability of the stochastic models used in the RTK

module and the rigorous approach, taking into account

inter-baseline correlation as well as the correlation in-

between each baseline component.

1 Introduction

1.1 RTK GPS Positioning

The most challenging mode among all the kinematic GPS

techniques is long range instantaneous RTK, while no

data accumulation is made throughout the adjustment

process. With longer distances to the reference stations,

the RTK technology faces great challenges, since many

distance-dependent biases (atmospheric, orbital errors,

etc.) need to be precisely modeled. If not properly

accommodated, these effects may seriously corrupt the

positioning and time transfer results. The success of

precise GPS positioning over long baselines depends on

the ability to resolve the integer phase ambiguities when

short observation time spans are required, which is

especially relevant to RTK applications (IAG SSG 1.179,

2000-2003). Instantaneous ambiguity resolution has

several advantages over the on-the-fly (OTF) method; it

is resistant to negative effects of cycle slips and can

provide immediate centimeter level positioning accuracy

without any delay needed for initialization as required by

the OTF technique (Pratt et al., 1998). However, the

ambiguity resolution can only be achieved if the

atmospheric, orbital and timing errors are properly

accounted for.

Over the past few years, the use of a GPS reference

station network approach has shown great promise in

extending the inter-receiver separation. The

implementation of multiple reference stations in a

permanent array offers several advantages over the

standard single-baseline approach. It improves the

accuracy of the mobile receiver and makes the results less

sensitive to the length of the rover-reference baselines

(Chen et al., 2000; Dai et al., 2001; Cannon et al., 2001).

Consequently, the precision of the baseline components,

Key words: RTK, GPS, Datum Definition

Some results presented here were reported at ION GNSS 2003, Portland, OR

Kashani et al.: Datum Definition in the Long Range Instantaneous RTK GPS Network Solution 101

in terms of their standard deviation is improved. The

most important contribution of the network solution, as

compared to the baseline approach, is not, however, the

improvement in precision, but rather the improvement in

the reliability and availability, as well as the new

possibilities for modeling atmospheric errors (Marel,

1998). Moreover, it is still possible to get an acceptable

solution even if there are gaps, outliers or cycle slips in

some of the reference station data.

1.2 Geodetic Control and Datum Definition

Observation equations relating to any geodetic network

are normally rank-deficient due to the lack of datum

reference. There is, therefore, a need to define the datum

in order to solve for the positioning parameters. Datum

definition can be accomplished by a careful selection of

some constraints added to the observation equation

model. This could be done while fixing one or more

reference stations during the adjustment procedure. When

only one reference station is held fixed we establish a

datum referred to as a minimum constraint solution; if

more than one station is fixed, the datum will be referred

to as an over-constrained solution. For a free network

approach, it is often desirable that the property of the

minimum sum of the variances and minimum sum of

squares of the correction to the coordinates is restricted to

certain points (Koch, 1999). These points are

undoubtedly those that correspond to the reference points

in the geodetic network. When dealing with GPS

multiple reference station processing, the CORS stations

should be considered a high order reference network.

Free net adjustment techniques play a major role in the

analysis of geodetic networks. Free networks are very

popular in geodesy, surveying and mapping, mainly due

to their unique property of being independent of errors in

external data. The results of the free net adjustment and

their superior quality serve as an authentic reflection

(undistorted mirror image) of the measurement quality

(Papo, 1999). There are several unique properties of the

free networks, as follows:

• The estimated accuracies of the coordinates are

optimal (Meissl, 1969). They depend solely on the

actual accuracies of the measurements. One of the

most important properties of a free network adjustment

is that of generating the minimum trace in the

dispersion matrix of the unknowns (Fritsch and

Schafrin, 1982).

• They are an unbiased representation of the adjusted

measurements.

• The coordinates of the network points define the

coordinate system. A more flexible approach may be

adopted by applying weights to these coordinates

(WFN).

In order to evaluate the quality and effectiveness of the

WFN approach, two more methods using different, datum

definition were tested; these are the minimum constraints

(MC) and the over-constrained (OC) methods, and the

comparison between the three models was carried out.

The results show noticeable improvements with respect

to the mean and standard deviation (STD) in the

estimated rover coordinates while using the suggested

WFN approach.

1.3 The MPGPSTM Software

The MPGPSTM software, currently under development at

OSU, includes different processing modules. The primary

goal of the development of the instantaneous RTK

module is to achieve reliable instantaneous real-time

solutions for distances over 100 km from the reference

stations. In order to accomplish this goal, a multi-

reference station approach is implemented. This paper

presents the test results from the current software

implementation, based on the actual field data. The

results analyzed here were obtained using instantaneous

processing and the ambiguity resolution technique in the

post-processing mode. The method is, however, suitable

for real time.

At the current stage of the software development, we

assume a unidirectional radio link from the reference

network stations (CORS) to the user receiver (rover). The

implemented algorithm is based on the double-

differences (DD) mode, which requires receiving

observations from one or more reference stations (i.e.

baseline or network solution). It should be noted that all

the processing is carried out at the rover. The

applicability of the unidirectional radio link was tested by

the Federal Highway Administration (FHWA) over long

distance, and real-time kinematic application was

demonstrated at 250 km (Remondi, 2002).

The ongoing developments of the MPGPSTM software

include transmitting the DD atmospheric corrections

derived from the reference network stations. These

corrections may further increase the system capabilities,

allowing for increased rover-network distances.

1.4 The VCV Matrix

The reliability of the variance-covariance (VCV) matrix

of the estimated parameters is of great importance,

especially in a multi-station processing mode (i.e.

network-based solution), when several baselines are

processed together (Kashani, 2002). The estimation of a

realistic VCV matrix by GPS processing software is a

function of the measurement weights (e.g. phase and

code) and the stochastic models taking into account both

mathematical and physical correlation between the

102 Journal of Global Positioning Systems

measurements. While the mathematical correlation can be

easily modeled, the physical correlation, unfortunately, is

more complicated to model. Consequently, if simplified

stochastic models are used, overly optimistic statistics

might result even in more comprehensive software,

which processes the measurements in a multi-station

mode, and produce a fully populated VCV (i.e.

considering the between baselines mathematical

correlation).

VCV matrices derived from a number of the existing

GPS software might not be realistic, especially in the

case of commercial packages (Howind et al., 1999). The

practical implication is that the produced accuracies are

too good, while the derived coordinates are in fact less

accurate. Therefore, a wrong decision could be made,

based on the software-derived accuracies, that the

solution the software presents is reliable and acceptable.

The majority of the GPS processing software packages

consider the VCV matrix of the observations to be either

diagonal - i.e., no correlation is considered, or block

diagonal - i.e., only the mathematical correlation is

considered (El-Rabbany et al., 2003).

All the modules in the MPGPSTM software include

rigorous stochastic models. The stochastic model used in

the network-based RTK module, which is based on DD

measurements, includes the inter-baseline mathematical

correlation (i.e., fully populated matrix). Even though,

the physical correlations are not taken into account, the

presented accuracy analysis indicates that the VCV

matrix seems realistic, rendering convincing coordinate

standard deviations.

2 Methodology

In this section, the review of the parameter estimation

procedure based on the model of DD GPS observations is

given, with a particular emphasis on different network

adjustment strategies. In general, the instantaneous RTK

software Module consists of three major steps as

presented by Kashani et al. (2003):

1. Float solution - based on network adjustment.

2. Integer ambiguity estimation - using the classical

wide-lane and 60/77 search algorithm.

3. Fixed solution - network adjustment introducing the

fixed ambiguities.

The parameter estimation is carried out by the least-

squares principle. An elevation-depended stochastic

model (weighting scheme) and mathematical correlation

including inter-baseline and baseline-component

correlations were taken into account and applied in the

algorithm. In addition, a fast Cholesky decomposition

was applied during the adjustment process. The network

solution was performed including all the independent

baselines in the network (i.e. from all the reference

stations to the rover).

2.1 Instantaneous RTK

2.1.1 Float Network Solution

The instantaneous RTK algorithm requires the use of

both the pseudo-range and phase observations due to the

low redundancy. Hence, the DD observation equations

for the GPS measurements are as follows:

1,1 1,

2,122 2,

2,1 2

(/)

klklkl klkl

ijij ijijij

klkl klklkl

ijij ijijij

klklkl kl

ijij ijij

klkl klkl

ijij ijij

TI N

TffI N

PTI

PTffI

Φρ λ

=+− +

=++



(1)

Where:

nij

DD phase observation on frequency n (n=1,2)

nij

P DD code observation on frequency n

DD geometric distance

T DD tropospheric delay

DD ionospheric delay

,ff

first and second GPS frequencies

while i,j denote the two receivers and k,l the two

satellites.

The Modified Hopfield model was used to calculate the

tropospheric DD corrections (T), and the DD

ionospheric delay (

) parameters were estimated in the

adjustment procedure. Thus, the adjustment model

becomes a simple one including only three types of

unknowns: rover coordinates (and some reference station

coordinates in the MC and the WFN), DD ambiguities,

and the DD ionospheric delay parameters.

The system of observation equations, which after

linearization with respect to the unknown parameters

gives the linear system of equations, is presented in

equation (2):

VLAX

= (2)

Where:

L Measured minus computed measurement

V Measurement corrections

Kashani et al.: Datum Definition in the Long Range Instantaneous RTK GPS Network Solution 103

A Design matrix relating measurements and

coordinates 11,2,

21,

ˆˆ

()

ˆˆ

(6077 )

kl kl

ij ij

kl kl

ij ij

Kround NN

K round NN

=−

X Corrections to the approximate unknowns

This approach deals with the DD code and phase

measurements from one pair of satellites and receivers at

a time that we call “one at a time” approach. Thus, at this

stage the network was decomposed to individual DD

pairs in order to fix the ambiguities. Although only a

particular combination yields the correct integer solution

for the two ambiguity sets, the 1

and 2

values may

not be free of errors. Consequently, not all of the

ambiguities can be recovered to their correct integer

values, especially for longer baselines. However, in the

test data analyzed here, almost all the ambiguities (96%)

were successfully fixed to their integer values. Since the

primary objective of this paper is the demonstration and

performance of the WFN approach, we do not

concentrate on the ambiguity search and validation

techniques here, but rather on the practically achievable

accuracy within the current software/algorithmic

configuration.

The unknown parameters X and the corresponding design

matrix A could be subdivided with respect to the

unknown ambiguities and the remaining parameters (i.e.,

the baseline components and the ionospheric delay

parameters), as follows:

112 2

VLAx Ax+= + (3)

Where 1

and the corresponding design matrix 1

refer

to the ambiguities; 2

and the corresponding design

matrix 2

refer to the remaining parameters.

As a result of the float network solution, real valued

estimates for both the ambiguities and the baseline

components are obtained, together with their

corresponding VCV matrices. Following Teunissen

(1998), the resulting float network adjustment solution

and its VCV matrix will be:

112

21 2

ˆˆˆ

ˆˆ ˆ

ˆ;

xxx

xx x

xQQ



 

 

 

(4)

2.1.3 Fixed Solution

Once the fixed solution 1

 has been obtained, as

described in the previous section, the ambiguity residuals

-1

) are used to correct the float solution 2

in order

tofinal positioning solution for the rover, prod

uce the

()



, shown in equation (6) (Teunissen 1998):

The solution of the integer least-squares problem is

denoted as 1

 and 2

; the corresponding float solution is

denoted as 1

and2

; 1

Q is the VCV matrix of1

; 2

is the VCV matrix of2.

12 1

ˆˆˆ

221 211

ˆˆ ˆ

()( )

xx x

xxxQQxx

−

==− −

 

(6)

2.1.2 Wide-Lane Ambiguity Search This equation refers to the relationship between the float

and the fixed solutions. It shows how the deference

between these two rover coordinate estimates depends on

the difference between the real-valued least squares

ambiguity estimates, 1

, and the integer least-squares

ambiguity estimate,1

. In order to get the VCV matrix of



one should apply the law of error propagation to (6) as

follows:

At this stage of the algorithm, the real-valued ambiguities

, denoted as and , from the float network

solution are fixed to their integer values,

ˆkl

N2,

ˆkl

, designated

as and . This step follows the classical wide-

lane and 60/77 search method with the integer

approximation on baseline-by-baseline basis (Yang et al.,

1994):



221212

ˆˆˆˆˆ

xxxxx

QQQQQ

−

=−

x

(7)

2,1 2

1,2, 1

(60) /17

kl kl

ij ij

NKK

NNK

=−

=+ (5)

2.2 Free-Net Adjustment Approach

Where:

The mathematical model of n measurements, which

produces a set of n observation equations linearized at the

approximated values of the coordinates, is given in

equation (2). The basis of the null space of A (Papo,

N and are the integer ambiguities from the center

of the search space.

104 Journal of Global Positioning Systems

According to Wolf (1977), any two X vectors, which

pertain to two different datums - for example, Xm and Xk,

- are related through the following simple equation:

1987), known also as the Helmert transformation matrix

E, has the following important property:

0AE = (8)

Datum based on selected m points is defined by

subjecting the vector X in (2) to the following linear

constraints (Papo and Perelmuter, 1981; Papo, 1986;

Papo, 1989):

EPXE X== (9)

where:

EP=E

and

PP=

mk k

XEt

+ (12)

where tkm is a d vector containing transformation

parameters from the k - to the m - datum. The solution for

tkm is derived from (12) under the minimum condition

(10), as follows (Wolf, 1977 and Papo, 1987):

()

kmmmkm k

tEEEXH

−

=−=− X (13)

When using a network-based approach with CORS

stations in RTK mode, only the CORS station coordinates

should be used to establish a datum, and the solution

should be the m-datum one, as presented in equation (9).

The Pm diagonal matrix entries include zeros or ones, and

define the datum points by setting ones in the correct

places. This solution is known as a “Weighted Free Net”

(WFN) adjustment. However, the Pm matrix could be

populated by different weights for the datum-defining

points, such as distance-dependent weights, as presented

here. Moreover, any a priori information, such as VCV

matrix of the CORS station coordinates, could also

replace the respective entries in the Pm matrix (Kashani,

2002).

Equation (10) is derived from seeking a minimum of the

following quadratic form:

min.

XPX= (10)

First, we minimize the VP quadratic form in order to

create the set of normal equations:

NX U= (11)

The above set is singular due to the need for datum

definition. It can be solved only if we apply at least d

independent linear constraints, as the order of the datum

defect to X. If, for example, we apply (9) to (11), we will

obtain a particular solution denoted as Xm. There is an

infinite number of sets of d constraints, which, when

applied to (11), will produce different solution vectors X,

all of which satisfy the normal equation (11).

3 Experiment

3.1 Data Source

The results shown herein were generated from

a static network of the Ohio CORS

(http://www.dot.state.oh.us/aerial/Cors.asp). In addition

to the three reference stations: SIDN, COLB and LEBA

from the Ohio CORS, a City of Dayton CORS static

station served as a rover. Figure 1 shows the test network

with the analyzed baselines marked. All the stations were

equipped with TRIMBLE 5700 high quality geodetic

receivers and antennas. The reference stations were

equipped with choke-ring GPS antennas, and the Dayton

station was connected to a geodetic antenna.

Let us consider one particular branch of such solutions,

which is characterized by the contents of the Pm weight

matrix. Out of the multitude of Pm matrices (and

respective datums), there is one particular solution, which

is unique, since the Pm matrix is equal to the identity

matrix. We will denote that unique solution as Xk. In this

case, m=k when each of the k points in the network

contributes to the datum definition on an equal basis, as

Pk=I.

Meissl (1969) and Koch (1999) have shown that such a

solution, as compared to the rest of the existing solutions,

is optimal and unique in the sense that the trace of the

VCV matrix is minimum. In addition, it can be shown

(Koch, 1999) that Qk, the un-scaled (σ0

2) VCV matrix of

X, is the pseudo-inverse of N, known also as the Moore-

Penrose inverse of N (Qk = N+). According to Meissl

(1969), the above optimal solution is the only one that

faithfully reflects the accuracy of the measurements,

where all the other (external) sources of error have been

effectively filtered out.

This reference-rover configuration reflects a possible

scenario common in surveying practice. Precise dual

frequency data collected on August 03, 2003 at a

sampling rate of 30-seconds for 13 hours between 00:00-

13:00 UT were used. A total of 1588 observation epochs

with the phase-smoothed code (Springer, 1999) and

carrier phase measurements were processed and

analyzed. The distances between the reference stations

varied from 98 to 121 km, and the distances to the rover

ranged from 40 to 100 km. The GPS data were collected

under moderate geomagnetic and ionospheric conditions

with the maximum Kp value reaching 3+.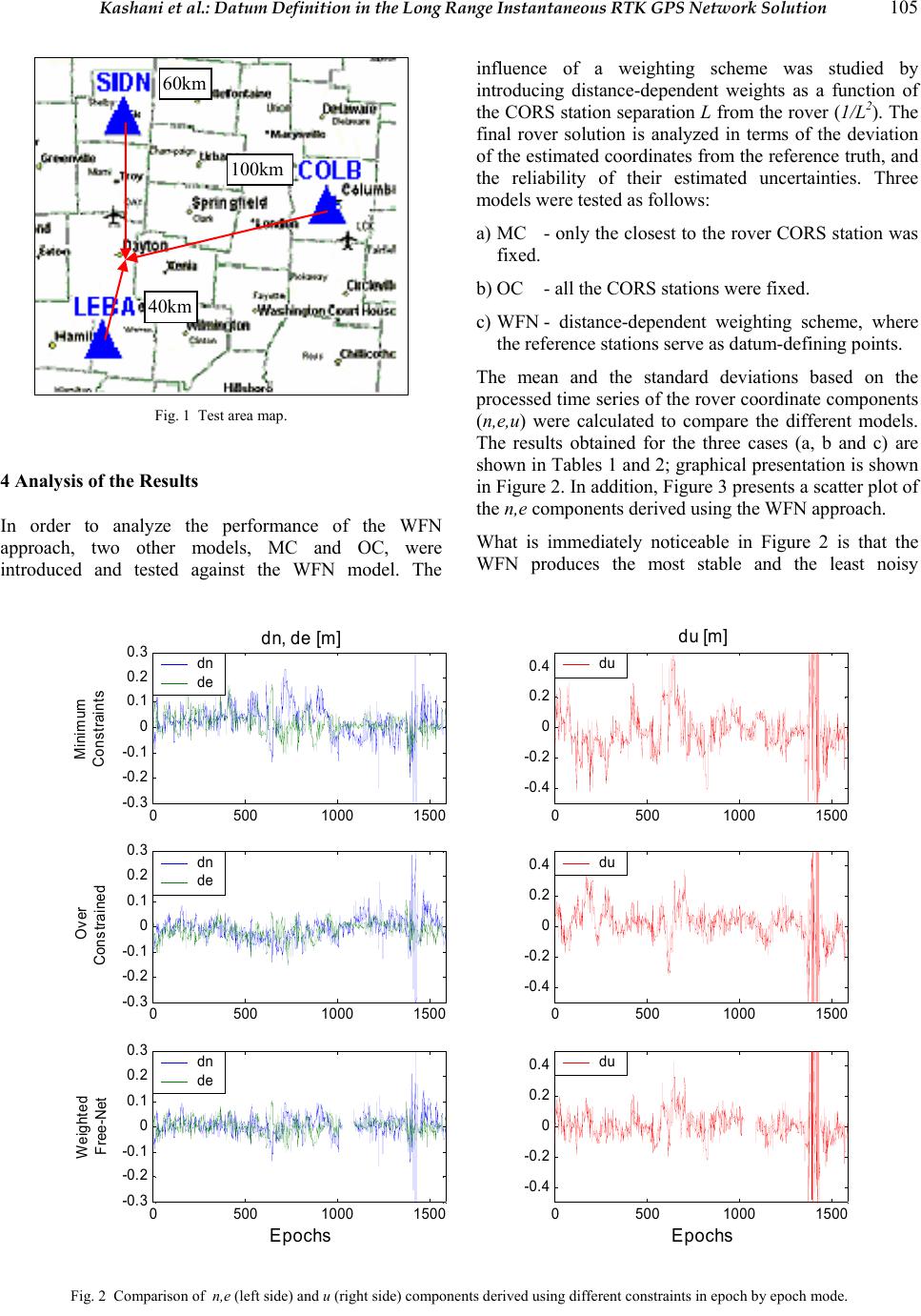

Kashani et al.: Datum Definition in the Long Range Instantaneous RTK GPS Network Solution 105

Fig. 1 Test area map.

4 Analysis of the Results

In order to analyze the performance of the WFN

approach, two other models, MC and OC, were

introduced and tested against the WFN model. The

influence of a weighting scheme was studied by

introducing distance-dependent weights as a function of

the CORS station separation L from the rover (1/L2). The

final rover solution is analyzed in terms of the deviation

of the estimated coordinates from the reference truth, and

the reliability of their estimated uncertainties. Three

models were tested as follows:

60km

40km

100km

a) MC - only the closest to the rover CORS station was

fixed.

b) OC - all the CORS stations were fixed.

c) WFN - distance-dependent weighting scheme, where

the reference stations serve as datum-defining points.

The mean and the standard deviations based on the

processed time series of the rover coordinate components

(n,e,u) were calculated to compare the different models.

The results obtained for the three cases (a, b and c) are

shown in Tables 1 and 2; graphical presentation is shown

in Figure 2. In addition, Figure 3 presents a scatter plot of

the n,e components derived using the WFN approach.

What is immediately noticeable in Figure 2 is that the

WFN produces the most stable and the least noisy

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

dn, de [m]

Minimum

Constraints

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

Over

Const rained

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

Weighted

F ree-Net

05001000 1500

-0.4

-0.2

0.2

0.4

du [m]

05001000 1500

-0.4

-0.2

0.2

0.4

05001000 1500

-0.4

-0.2

0.2

0.4

EpochsEpochs

Fig. 2 Comparison of n,e (left side) and u (right side) components derived using different constraints in epoch by epoch mode.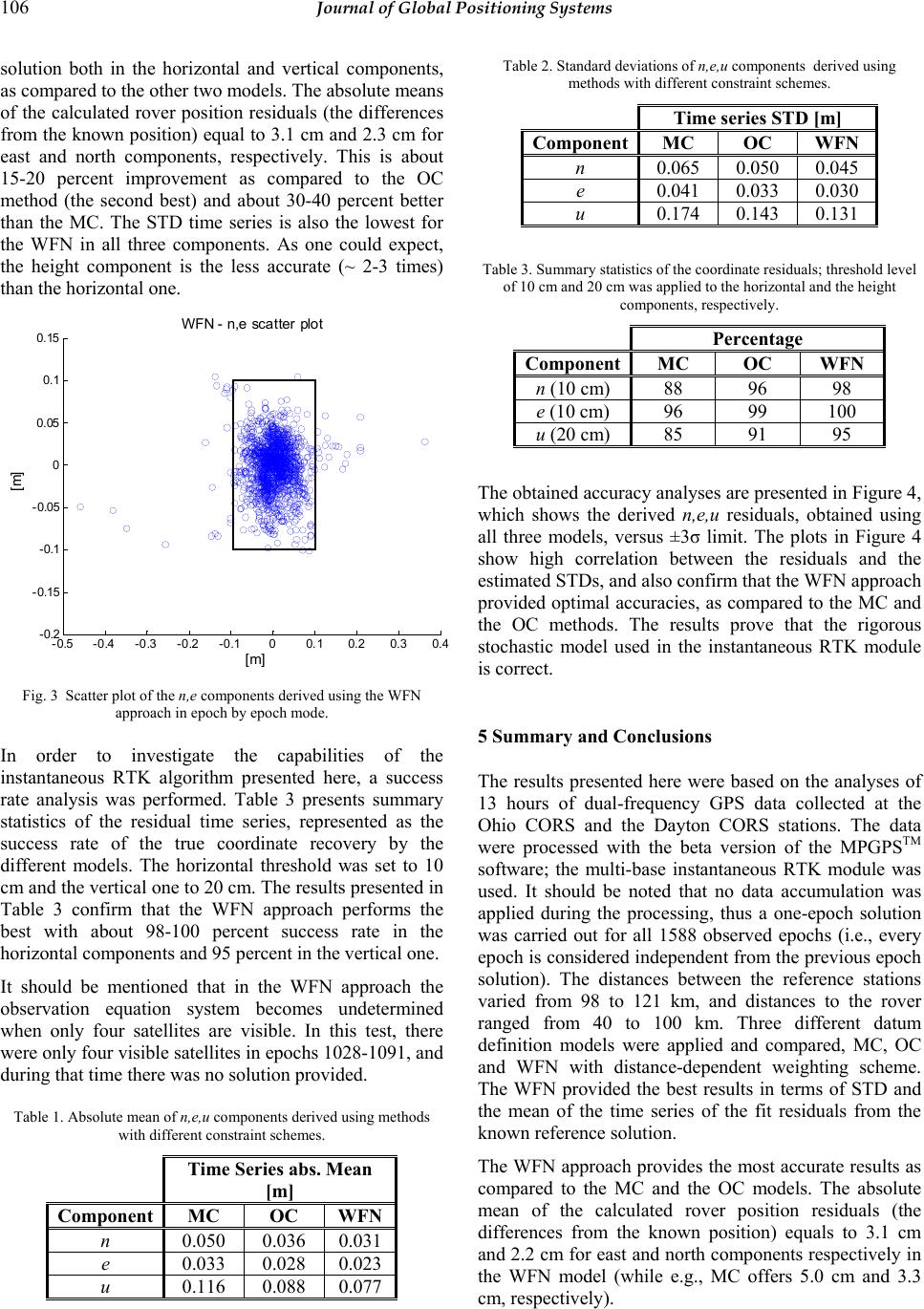

106 Journal of Global Positioning Systems

solution both in the horizontal and vertical components,

as compared to the other two models. The absolute means

of the calculated rover position residuals (the differences

from the known position) equal to 3.1 cm and 2.3 cm for

east and north components, respectively. This is about

15-20 percent improvement as compared to the OC

method (the second best) and about 30-40 percent better

than the MC. The STD time series is also the lowest for

the WFN in all three components. As one could expect,

the height component is the less accurate (~ 2-3 times)

than the horizontal one.

Table 2. Standard deviations of n,e,u components derived using

methods with different constraint schemes.

Time series STD [m]

ComponentMC OC WFN

n 0.065 0.050 0.045

e 0.041 0.033 0.030

u 0.174 0.143 0.131

Table 3. Summary statistics of the coordinate residuals; threshold level

of 10 cm and 20 cm was applied to the horizontal and the height

components, respectively.

-0.5 -0.4 -0.3 -0.2 -0.100.1 0.20.30.4

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

WFN - n,e scatter plot

[m]

Percentage

ComponentMC OC WFN

n (10 cm) 88 96 98

e (10 cm) 96 99 100

u (20 cm) 85 91 95

The obtained accuracy analyses are presented in Figure 4,

which shows the derived n,e,u residuals, obtained using

all three models, versus ±3σ limit. The plots in Figure 4

show high correlation between the residuals and the

estimated STDs, and also confirm that the WFN approach

provided optimal accuracies, as compared to the MC and

the OC methods. The results prove that the rigorous

stochastic model used in the instantaneous RTK module

is correct.

Fig. 3 Scatter plot of the n,e components derived using the WFN

approach in epoch by epoch mode.

5 Summary and Conclusions

In order to investigate the capabilities of the

instantaneous RTK algorithm presented here, a success

rate analysis was performed. Table 3 presents summary

statistics of the residual time series, represented as the

success rate of the true coordinate recovery by the

different models. The horizontal threshold was set to 10

cm and the vertical one to 20 cm. The results presented in

Table 3 confirm that the WFN approach performs the

best with about 98-100 percent success rate in the

horizontal components and 95 percent in the vertical one.

The results presented here were based on the analyses of

13 hours of dual-frequency GPS data collected at the

Ohio CORS and the Dayton CORS stations. The data

were processed with the beta version of the MPGPSTM

software; the multi-base instantaneous RTK module was

used. It should be noted that no data accumulation was

applied during the processing, thus a one-epoch solution

was carried out for all 1588 observed epochs (i.e., every

epoch is considered independent from the previous epoch

solution). The distances between the reference stations

varied from 98 to 121 km, and distances to the rover

ranged from 40 to 100 km. Three different datum

definition models were applied and compared, MC, OC

and WFN with distance-dependent weighting scheme.

The WFN provided the best results in terms of STD and

the mean of the time series of the fit residuals from the

known reference solution.

It should be mentioned that in the WFN approach the

observation equation system becomes undetermined

when only four satellites are visible. In this test, there

were only four visible satellites in epochs 1028-1091, and

during that time there was no solution provided.

Table 1. Absolute mean of n,e,u components derived using methods

with different constraint schemes.

The WFN approach provides the most accurate results as

compared to the MC and the OC models. The absolute

mean of the calculated rover position residuals (the

differences from the known position) equals to 3.1 cm

and 2.2 cm for east and north components respectively in

the WFN model (while e.g., MC offers 5.0 cm and 3.3

cm, respectively).

Time Series abs. Mean

[m]

Component MC OC WFN

n 0.050 0.036 0.031

e 0.033 0.028 0.023

u 0.116 0.088 0.077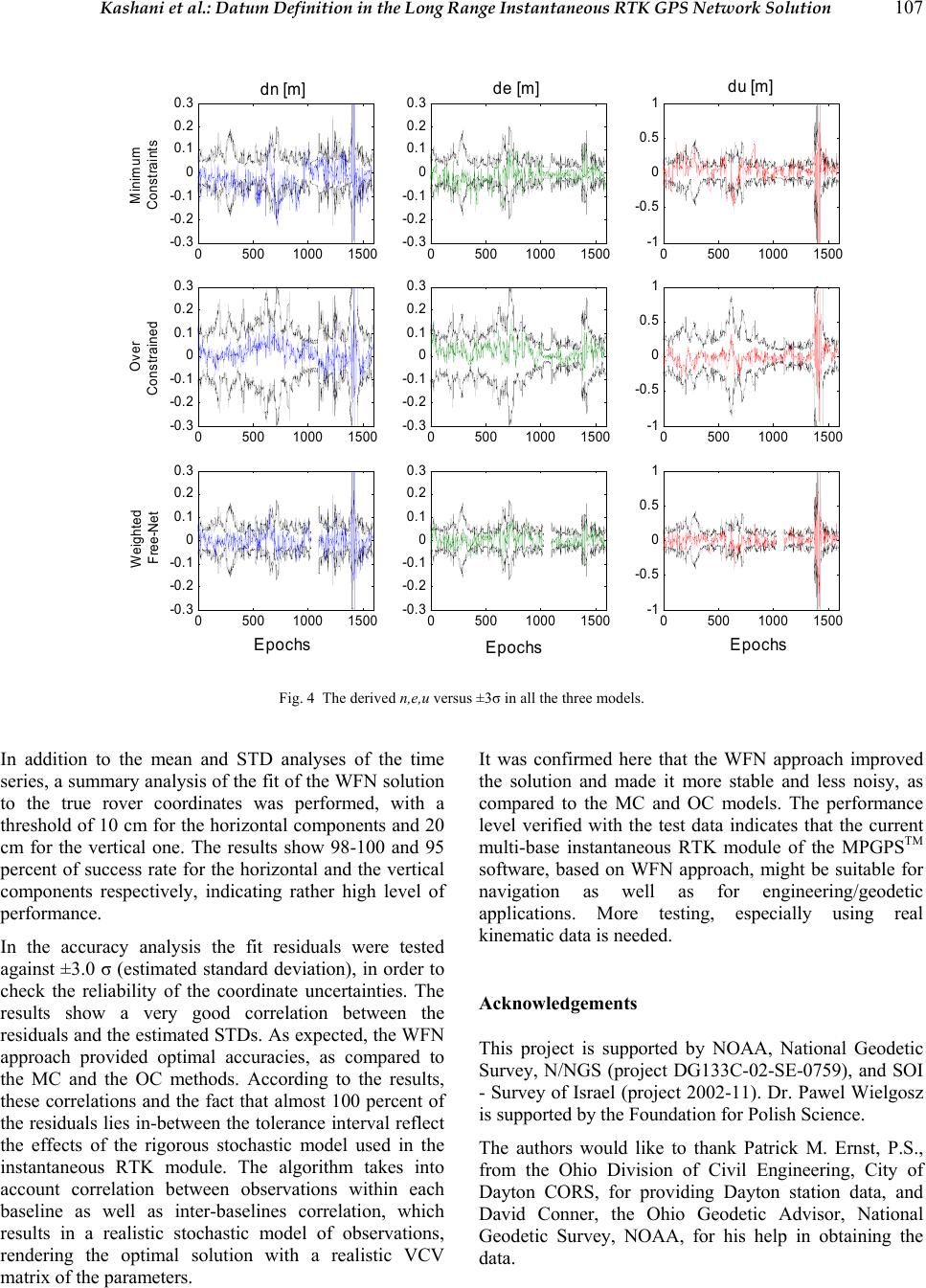

Kashani et al.: Datum Definition in the Long Range Instantaneous RTK GPS Network Solution 107

0500 1000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

dn [m]

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

de [m]

05001000 1500

-1

-0.5

0.5

du [m]

0500 1000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

05001000 1500

-1

-0.5

0.5

0500 1000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

05001000 1500

-0.3

-0.2

-0.1

0.1

0.2

0.3

05001000 1500

-1

-0.5

0.5

Minimum

Cons traints

Over

Constrained

Weighted

Free-Net

Epochs

Epochs Epochs

Fig. 4 The derived n,e,u versus ±3σ in all the three models.

In addition to the mean and STD analyses of the time

series, a summary analysis of the fit of the WFN solution

to the true rover coordinates was performed, with a

threshold of 10 cm for the horizontal components and 20

cm for the vertical one. The results show 98-100 and 95

percent of success rate for the horizontal and the vertical

components respectively, indicating rather high level of

performance.

It was confirmed here that the WFN approach improved

the solution and made it more stable and less noisy, as

compared to the MC and OC models. The performance

level verified with the test data indicates that the current

multi-base instantaneous RTK module of the MPGPSTM

software, based on WFN approach, might be suitable for

navigation as well as for engineering/geodetic

applications. More testing, especially using real

kinematic data is needed.

In the accuracy analysis the fit residuals were tested

against ±3.0 σ (estimated standard deviation), in order to

check the reliability of the coordinate uncertainties. The

results show a very good correlation between the

residuals and the estimated STDs. As expected, the WFN

approach provided optimal accuracies, as compared to

the MC and the OC methods. According to the results,

these correlations and the fact that almost 100 percent of

the residuals lies in-between the tolerance interval reflect

the effects of the rigorous stochastic model used in the

instantaneous RTK module. The algorithm takes into

account correlation between observations within each

baseline as well as inter-baselines correlation, which

results in a realistic stochastic model of observations,

rendering the optimal solution with a realistic VCV

matrix of the parameters.

Acknowledgements

This project is supported by NOAA, National Geodetic

Survey, N/NGS (project DG133C-02-SE-0759), and SOI

- Survey of Israel (project 2002-11). Dr. Pawel Wielgosz

is supported by the Foundation for Polish Science.

The authors would like to thank Patrick M. Ernst, P.S.,

from the Ohio Division of Civil Engineering, City of

Dayton CORS, for providing Dayton station data, and

David Conner, the Ohio Geodetic Advisor, National

Geodetic Survey, NOAA, for his help in obtaining the

data.

108 Journal of Global Positioning Systems

References

Cannon, M.E., G. Lachapelle, P. Alves, L.P. Fortes and B.

Townsend (2001) GPS RTK Positioning Using a

Regional Reference Network: Theory and Results,

Proceedings of 5th GNSS International Symposium,

Seville, May 8-11.

Chen, H.Y. (2000) An instantaneous ambiguity resolution

procedure suitable for medium-scale GPS reference

station networks, 13th Int. Tech. Meeting of the Satellite

Division of the U.S. Inst. of Navigation, Salt Lake City,

Utah, 19-22 September, pp. 1061-1070.

Dai, L., J. Wang, C. Rizos and S. Han (2001) Real-time carrier

phase ambiguity resolution for GPS/GLONASS reference

station networks, Int. Symp. on Kinematic Systems in

Geodesy, Geomatics & Navigation (KIS2001), Banff,

Canada, 5-8 June, p. 475-481.

El-Rabbany, A.E. (2003) Effect of Temporal Physical

Correlation on Accuracy Estimation in GPS Relative

Positioning, Journal of Surveying Engineering, Vol. 129,

No. 1, pp. 28-32.

Fritsch, D. and B. Schafrin (1982) The “Choice of Norn”

Problem for the Free Net Adjustment with Orientation

Parameters, Boll. Geod. Sci. Aff., Vol. 41, pp. 259-282.

Howind, J., H. Kutter and B. Heck (1999) Impact of temporal

correlation on GPS-derived relative point positions,

Journal of Geodesy, 73, pp. 246-258.

IAG SSG 1.179, Wide area modeling for precise satellite

positioning, Terms of Reference.

http://www.gfy.ku.dk/~iag/HB2000/part3/Sec1.htm, last

accessed in 2003.

Kashani, I., (2002) Geodetic control networks in the era of

permanent GPS stations, Ph.D thesis, Technion - Israel

Institute of Technology, 165p.

Kashani, I., P. Wielgosz and D. Grejner-Brzezinska (2003)

Free Net Adjustment in Multi Reference Stations

Approach for Instantaneous RTK, Proceedings, ION

GPS/GNSS, Sept 9-12, Portland, Oregon, pp. 1390-1396.

Koch, K.R. (1999) Parameter Estimation and Hypothesis

Testing in Linear Models, Springer Verlag, Berlin

Heidelberg New York, 333p.

Marel, H. van der (1998) Virtual GPS reference stations in

The Netherlands, Proc. of the 11th International Technical

Meeting, Algorithms and Methods ION-GPS '98,

Nashville, USA, 15-18 September 1998, part I: pp. 49-58.

Meissl, P. (1969) Inner Theory of Errors of a Cluster of

Points. Annex F in Systematic Investigations of Geodetic

Networks in Space, (ed) K. Rinner.

Papo, H. and A. Perelmuter (1981) Datum Definition by Free

Net Adjustment, Bulletin Geodesique, Vol.55, No.3.

Papo, H. (1986) Extended Free Net Adjustment Constraint,

NOAA Tech. Rep., NOS 119 NGS 37, Rockville MD.

Papo, H. (1987) Bases of Null Space in Analytical

Photogrammetry, Photogrammetria, Vol. 41.

Papo, H. (1989) Modeling in Non-Cartesian Reference

Frames, IAG General Meeting, Edinburgh, Scotland, UK.

Papo, H. (1999) Datum Accuracy and its Dependence on

Network Geometry, International Scientific and Technical

Conference, dedicated to the 220th anniversary of Moscow

State University of Geodesy and Cartography, May 24-29,

1999

Pratt, M., B. Burke and P. Misra (1998) Single epoch

ambiguity resolution with GPS-GLONASS L1-L2 data,

Proc. of the 11th International Technical Meeting,

Algorithms and Methods ION-GPS '98, Nashville, USA,

pp. 389-398

Remondi, B. W. (2002) Support of the System Test and

Analysis Program for the Nationwide Differential Global

Positioning System Modernization Program Phase I

High Accuracy-Nationwide Differential Global

Positioning System Report, FHWA-RD-02-110 (July

2002). http://www.tfhrc.gov/its/ndgps/02110/index.htm.

Springer, T.A. (1999) Modeling and Validating Orbits and

Clocks Using the Global Positioning System, Ph.D.

dissertation, Astronomical Institute, University of Berne,

Berne, Switzerland, 155p.

Teunissen, P.J.G and A. Kleusberg (Eds.), (1998) GPS for

Geodesy, Springer - Verlag Berlin Heidelberg New York,

650p.

Yang, M., C. Goad and B. Schaffrin (1994) Real-time on-the-

fly ambiguity resolution over short baseline in the

presence of anti-spoofing, in Proceedings of ION GPS-94,

Salt Lake City, pp. 519-525.