Applied Mathematics
Vol.05 No.19(2014), Article ID:51327,49 pages
10.4236/am.2014.519298
Modeling the Dynamics of Malaria Transmission with Bed Net Protection Perspective
Jean Claude Kamgang1, Vivient Corneille Kamla1, Stéphane Yanick Tchoumi2
1Department of Mathematics and Computer Sciences, ENSAI, University of N’Gaoundéré, N’Gaoundéré, Cameroon
2Department of Mathematics and Computer Sciences, Faculty of Science, University of N’Gaoundéré, N’Gaoundéré, Cameroon
Email: jckamgang@gmail.com, vckamla@gmail.com, sytchoumi83@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 September 2014; revised 15 October 2014; accepted 29 October 2014
ABSTRACT
We propose and analyze an epidemiological model to evaluate the effectiveness of bed nets as a prophylactic measure in malaria-endemic areas. The main purpose in this work is the modeling of the aggressiveness of anopheles mosquitoes relative to the way humans use to protect themselves against bites of mosquitoes. This model is a system of several differential equations: the number of equations depends on the particular assumptions of the model. We compute the basic re- production number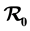 , and show that if
, and show that if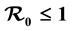 , the disease free equilibrium (DFE) is globally asymptotically stable on the non-negative orthant. If
, the disease free equilibrium (DFE) is globally asymptotically stable on the non-negative orthant. If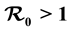 , the system admits a unique endemic equilibrium (EE) that is globally and asymptotically stable. Numerical simulations are presented corresponding to scenarios typical of malaria-endemic areas, based on data collected in the literature. Finally, we discuss the relative effectiveness of different kinds of bed nets.
, the system admits a unique endemic equilibrium (EE) that is globally and asymptotically stable. Numerical simulations are presented corresponding to scenarios typical of malaria-endemic areas, based on data collected in the literature. Finally, we discuss the relative effectiveness of different kinds of bed nets.
Keywords:
Epidemiological Model, Malaria, Basic Reproduction Number, Lyapunov Function, Global Asymptotic Stability, Non-Standard Finite Difference Scheme (NFDS), Simulation

1. Introduction
Malaria is a vector-borne infectious disease that is widespread in tropical regions, including parts of America, Asia and much of Africa. Humans contract malaria following effective bites of infected Anopheles female mosquitoes during blood feeding. Plasmodium falciparum is the most common cause of malaria mortality in Africa, and the chain of transmission can be broken through the use of insecticide-treated bed nets and anti-malarial drugs, as well as other control strategies.
Malaria accounts for more than 207 million infections and results in over 627,000 deaths globally in 2012 [1] . About 90% of these fatalities occur in Sub-Saharan Africa [1] [2] . Despite intensive social and medical research and numerous programs to combat malaria, the incidence of malaria across the African continent remains high.
In the field of mathematical epidemiology, numerous models have been proposed with the purpose of under- standing various aspects of the disease. The foundation model of Sir Ronald Ross, originally proposed in 1911 [3] and extended by MacDonald in 1957 [4] , serves as the basis for many mathematical investigations into the epidemiology of malaria. A prominent example is the model of Ngwa and Shu [5] , which introduces susceptible (S), exposed (E), and infectious (I) classes for both humans and mosquitoes, plus an additional Immune class (R) for humans. This model is extended in the Ph.D. theses of Chitnis [6] and Zongo [7] (these two theses also provide comprehensive reviews on the state of the art). Chitnis introduces immigration into the host population, which is a significant effect since hosts migrating from a naive region to a region with high endemicity are especially susceptible to infection. Zongo further extends the model by dividing the human population into non- immune and semi-immune sub-populations, which are modeled using (SEIS) and (SEIRS) model types, respectively.
In his thesis, Chitnis espoused the use of insecticide-treated bed nets, coupled with rapid medical treatment of new cases of infection, as the best strategy to combat malaria transmission. In this paper we make further extensions to the model to include the effects of bed-net use on malaria transmission. In particular, we divide the human population into groups that are characterized by the methods they use to protect themselves against the mosquito bites. These assumptions are consistent with the observable situation in many endemic areas, parti- cularly in poor countries. We believe that the current study represents the first systematic model-based analysis of the impact of bed nets on the dynamics of malaria transmission.
Malaria is highly seasonal [8] [9] : the highest endemicity typically occurs during rainy seasons, when mosquito density is high due to high humidity and the presence of standing water where mosquitoes can breed. During this period, even people with immune predisposition to malaria infection are at risk of attaining the critical level of malaria parasites in their bloodstream that could make them fall sick. In our model, we consider conditions characteristic of a rainy season in a region of high malaria endemicity: typically, such conditions last for a period between three to six months. Because of the brevity of the period being considered, we neglect the effects of death, birth and migration of hosts. We also omit exposed and recovered classes for hosts: due to the high density of anopheles mosquitoes during such periods, exposed individuals rapidly become infectious, and the partial immunity of hosts following recovery has negligible effect. Results for more sophisticated models that include exposed and/or recovered state(s) are reserved for forthcoming papers.
The paper is organized as follows. Section 2 describes our model and gives the corresponding system of differential equations. Section 3 establishes the well-posedness of the model by demonstrating invariance of the set of non-negative states, as well as boundedness properties of the solution. The equilibriums of the system are calculated, and a threshold condition for the stability of the disease free equilibrium (DFE) is calculated, which is based on the basic reproduction number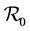 . The method used to derive the basic reproduction number is different for the method of the next generation operator of Van Den Driesshe and Watmough [10] currently used in literature. Section 4 analyzes the stability of equilibriums. We prove in Section 4.1 the global asymptotic stability (GAS) of the disease free equilibrium (DFE) when
. The method used to derive the basic reproduction number is different for the method of the next generation operator of Van Den Driesshe and Watmough [10] currently used in literature. Section 4 analyzes the stability of equilibriums. We prove in Section 4.1 the global asymptotic stability (GAS) of the disease free equilibrium (DFE) when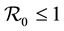 ; in Section 4.2 we prove the GAS of the endemic equilibrium (EE) when
; in Section 4.2 we prove the GAS of the endemic equilibrium (EE) when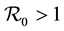 . Section 5 provides graphs of trajectories corresponding to various parameter sets computed based on data obtained from the literature. Section 6 discusses the significance of our results. Finally, the Appendix contains detailed proofs and computations required by the analysis.
. Section 5 provides graphs of trajectories corresponding to various parameter sets computed based on data obtained from the literature. Section 6 discusses the significance of our results. Finally, the Appendix contains detailed proofs and computations required by the analysis.
2. Model Description and Mathematical Specification
The model assumes an area populated by
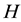 human hosts and
human hosts and
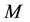 female mosquitoes (disease vectors) under conditions of higher endemicity of malaria. The human and mosquito populations are homogeneously mixed. In the following subsections, we provide a detailed description of the population structure and dynamics of hosts and vectors.
female mosquitoes (disease vectors) under conditions of higher endemicity of malaria. The human and mosquito populations are homogeneously mixed. In the following subsections, we provide a detailed description of the population structure and dynamics of hosts and vectors.
2.1. Host Population Structure and Dynamics
The human population is divided into
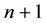 groups. One of these groups consists of humans who do not use bed nets, while the other
groups. One of these groups consists of humans who do not use bed nets, while the other
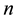 groups correspond to the various types of bed nets used as protection against mosquito bites. Some nets are untreated; others are treated with repellent; others are treated with insecticides, with varying degrees of toxicity (toxicity typically decreases with use). We let
groups correspond to the various types of bed nets used as protection against mosquito bites. Some nets are untreated; others are treated with repellent; others are treated with insecticides, with varying degrees of toxicity (toxicity typically decreases with use). We let
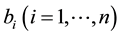 denote the proportion
denote the proportion
of the human population that is in the
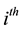 protected group, and
protected group, and
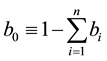 is the proportion of humans that
is the proportion of humans that
use no protection.
The dynamics of the
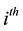 host population
host population
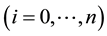 is described by a SIS-based compartment model as shown in Figure 1. As explained in the Introduction, we omit exposed and recovered classes, as well as the ef-
is described by a SIS-based compartment model as shown in Figure 1. As explained in the Introduction, we omit exposed and recovered classes, as well as the ef-
fects of birth, death, and migration. The incidence of infection for humans in the
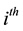 group is given by
group is given by
where a is the average number of bites per mosquito per unit time (the entomological inoculation rate);




2.2. Mosquito Population Structure and Dynamics
The population of disease vectors (adult female anopheles mosquitoes) is characterized by several classes, where each mosquito’s class membership is determined by its own history of past activity. Newly-emerged adult mosquitoes initially enter the susceptible class: the rate of entry (that is, the recruitment rate) is

Adult mosquitoes alternate between two activities: questing (that is, seeking a host to bite for its blood meal) and resting (to lay down eggs, or to digest a blood meal). In the current model we assume that all susceptible mosquitoes are in the questing state: the presence of susceptible resting mosquitoes can be approximately accommodated by reducing

Questing mosquitoes are equally likely to feed on any human, regardless of his/her protection method. Thus for any given blood meal, the probability that the human host belongs to the









we let




coming infected is
Susceptible mosquitoes that become infected enter the first exposed resting class
Figure 1. Dynamics of the

infectious after a fixed number l of resting/questing cycles following initial infection. These successive resting/
questing cycles are modeled as a sequence of


If a mosquito survives through all of these state, it then enters the infectious class, which is further divided into questing and resting sub-classes (

The overall dynamics of the mosquito population is depicted in the multi compartment diagram in Figure 2: The fundamental model parameters are summarized in Table 1, while derived parameters are summarized in Table 2.
Figure 2. Mosquito population dynamics.
Table 1. Fundamental model parameters.
Table 2. Derived model parameters.
2.3. Model Equations
The system of ordinary differential equations that characterize the model are given as follows:

The system (1) together with initial conditions completely specifies the evolution of the multi-compartment system shown in Figure 1 and Figure 2. Note that system (1) also determines



3. Well-Posedness, Dissipativity and Equilibria of the System
In this section we demonstrate well-posedness of the model by demonstrating invariance of the set of non- negative states, as well as boundedness properties of the solution. We also calculate the equilibriums of the system, whose stability properties will be examined in the following section.
3.1. Positive Invariance of the Non-Negative Cone in State Space
The system (1) can be rewritten in matrix form as

Equation (2) is defined for values of the state variable





represents the non-naive components of the state of the system. This notation is consistent with the notation of reference ([12] ), and we use results from this reference in our analysis.
The matrix


where the four matrices blocks may be described as follows:
The





The




terms of the first row, which are given by
vectors from the susceptible to the first exposed state, which depends on infectious the host components. The


entries are zero except the


from state


The






Remark 3.1. The second matrix form given in (2) can also be written in the form

where


the DFE (see Proposition 3.5 below) in the disease free sub-variety For such a system, Kamgang et al. in [12] gives a threshold condition for the stability of the DFE and an analysis of global asymptotic stability that we may apply to the current system.
For a given



The following proposition establishes that system (2) is epidemiologically well posed.
Proposition 3.1. The non-negative cone

Proof. For any

3.2. Boundedness and Dissipativity of the Trajectories
We have the following proposition.
Proposition 3.2. The simplex

where


ing set for the system (1).
Note that


Proof. From (1) we have


follows that








As a result of Proposition 2, we may limit our study to the simplex specified in (6).
3.3. Computation of the Threshold Condition
Several techniques exist for computing the basic reproduction number and threshold conditions for the local asymptotic stability of the disease free equilibrium of epidemiological models represented by systems of ordinary differential equations. In [10] the maximum eigenvalue of next generation operator is proposed. In many other papers in the literature, either the technique in [10] , or the Routh-Hurwitz criterion are used [13] - [15] . Unfortunately, these are not suitable for large-scale systems that may possess many equations. Instead, we use the technique in [12] to compute the threshold condition for the system under consideration, which also enables the evaluation of the basic reproduction number. Specifically, we have:
Proposition 3.3 ([12] ). Let



D are square matrices. Then




We refer the reader to reference [12] for the proof of the proposition. This result enables the reduction of the large-scale matrix

Proposition 3.4. The basic reproduction number for the system (1) is

where


The proof of the above proposition is postponed to Appendix B.
3.4. System Equilibria
Steady states of the system are specified by the following proposition.
Proposition 3.5. System (2) admits two equilibriums. The first (called the disease free equilibrium or DFE) is
given by



demic equilibrium or EE) is given by

where


The proof of Proposition 3.5 is postponed to Appendix C.
Remark 3.2. Equation (9) shows that the dynamics of the mosquito population (expressed in the parameters


4. Stability of System Equilibria
In this section we analyze the stability of the system equilibriums given in Proposition 3.5.
4.1. Global Asymptotic Stability of the Disease Free Equilibrium (DFE)
We have the following result for the global asymptotic stability of the disease free equilibrium:
Theorem 4.1. When

Proof. Our proof is based on Theorem 4.3 of [12] , which establishes global asymptotic stability for epidemiological systems that can be expressed in the matrix form (5). This theorem is restated as Theorem A.1 in the Appendix: for the proof, the reader may consult [12] . To complete the proof, we need only establish for the system (2) that the five conditions (h1)-(h5) required in Theorem A.1 are satisfied when
(h1) This condition is satisfied for the system (2) as a result of Proposition 2.
(h2) We note first that



duced to this sub variety is




(h3) We consider first the case



In this case, the two properties required for condition (h3) follow immediately: off-diagonal terms of the matrix




(h4) Defining





(h5) We first observe that






Figure 3. Graph associated to the matrix
Since the five conditions for Theorem 4.3 of [12] are satisfied, the theorem follows. □
4.2. Stability Analysis of Endemic Equilibrium (EE)
In this section we address the analysis of the behavior of the system when the condition

Theorem 4.2. When


Remark 4.1. The above theorem implies the GAS of the EE in the non-negative cone

Proof. Considering the system (1) when




where the coefficients,




With these positive constants,



Substituting the value of

Using relations between values of components of the state of the model at the EE given in Equation (8) (see Proposition 3.5) specifically
and after few algebraic arrangements, the above becomes:
Taking





The terms








whenever






the on the subset of


Using the fact that







It comes out that



5. Numerical Simulation
To illustrate results in this work, the system (1) is simulated using parameters value/range in the following Table 3 and Table 4. We assume in all our simulations the initial ratio of fifty vectors for one human, since the model assume an episode of high endemicity of the disease (i.e.














Table 3. Parameter values for vector population dynamics.
Note. Source of the estimation:
Table 4. Parameter values for host population dynamics.
We also assume different values of coefficients


We use for simulation Non-standard Finite Difference Scheme (NFDS) instead of classical ordinary differential packages that can be found in various scientific programming environment. The NFDS used is given in the Appendix D. As a matter of fact, the technique involved is designed by R. Anguelov et al. [33] as a numerical companion of [12] , that is well designed for system as ours (i.e. large scale system). Simulation using ode packages takes much time and solutions obtained, compared to those computed using NFDS are really less accurate.
5.1. Figures of Trajectories of Significatives Components of the States
Below, are plots of trajectories of significant components (when the time of the realization of the asymptotic stability is reasonable) of the states of the model (infectious hosts and infectious questing vector) or parametric curves (when the time of the realization of the asymptotic stability is very long) between significant components accompany by finishing sections of trajectories (to show how accurate the result produced by numerical scheme is) representing scenarios corresponding to set of data (with the corresponding values of the

5.1.1. Scenarios with One Protected Skill of Two Third of the Hosts with Net with Poor Killing Effect
Figures 4-11 show scenarios where humans are protected with bed nets with small killing effect (i.e.
and a repelling effect that increases from poor (see Figure 4, Figure 5, where

5.1.2. Scenarios with One Protected Skill of Two Third of the Hosts Using Net with Killing Effect
Figures 12-19 show scenarios where the killing effect of bed nets in protection skills is better (
Figures 20-27 are scenarios with one protection skill not corresponding to the section, and which, with parameters values have been chosen in order to compute situation of





5.1.3. Scenarios with One Protected Skill of Six Seventh of the Hosts Using Net
We now change the proportion of bed net users from two third to six seventh in scenarios corresponding to lowest feeding effects in figures (scenarios in Figure 10, Figure 18). Figures 28-31 show how important this impacts trajectories presented. It can be observed that the drop down of the endemicity happens quickly and strongly. e.g. in Figure 29, despite the value of

5.1.4. Scenarios with Two Protected Skills; Half Protected

For scenarios with two protections (






5.1.5. Scenarios with Three Protected Capabilities; Poor Protected

For scenarios with three protections (






Figure 32. Scenario with lower killing effect and poor protecting effect for





Figure 33. Scenario based on the same

since the components of infectious vectors behave nearly the same as what appears in scenarios with one protection in Figures 4-33 above, we present only figures of trajectories of the infectious hosts components of the state of the system (Figures 39). For chosen set of parameters such that









5.2. Comments on Figures
In the Graphical representation (Subsection 5.1 here above), we assumed a human population constituted in a




Figure 34. Scenario based on choice of


thousand of individuals and at any initial state, the size of vectors population is fifty time the size of the hosts population. We also assumed the hatching force of mosquitoes sufficiently high to figure situation of an area of higher malaria endemicity.
In all figures, we choose to present only coordinates of the states of the model corresponding to the infectious humans and infectious questing vectors, since they are the most relevant from the analysis in this paper. Figures 4-31 are plots of trajectories and parametric curves with the same initial states (three initial states) corresponding to scenarios based on one protection strategy. For values of













Figure 35. Scenario based on choice of


the endemicity regarding the level of the infectious hosts is still high. Figures 12-19 that correspond to scenarios where peoples are protected with bed nets with the killing effect












Figure 36. Finishing section of trajectories of infected host corresponding to parametric curves in Figure 34.
since the time of the realization of this stability was quite long and the finishing sections of trajectories (Figure 26, Figure 27) have been presented to let the obviousness of this stability appeared. What is enlightened in the presentation of these figures is the efficacy of the scheme used for our simulations. The Non Standard Finite Difference Scheme (NSFDS) of Anguelov et al. [33] is definitely established here as the unchangeable scheme for simulation of system like ours. (more than seventeen equations). Coming back to our initial goal, scenarios in Figures 28-31 are made up by increasing the proportion of protected bed net users in scenarios in Figure 10, Figure 11 and in Figure 18, and Figure 19 respectively. In these figures, it appears obviously and in all proportion how, when the great majority of hosts are bed net users, this impacts the endemicity of malaria. The area is quickly cleared from vectors, and the endemicity in term of the quantity of infected host drops down quickly.
Figures 32-38 are plots of trajectories (Figure 32, Figure 33 and Figure 38) and parametric curves with finishing sections of trajectories (Figures 34-37) with the same initial states (three initial states) representing scenarios based on two protection strategies (half protection indexed by






Figure 37. Finishing section of trajectories of infected host corresponding to parametric curves in Figure 35.
infectious questing mosquitoes component behave nearly in the same manner as those in plots of infectious questing mosquitoes components in Figures 4-31; we exclude them since they are very large files. Comparing Figure 32 and Figure 33, it comes out another presentation of the influence of the killing effect of the bed net protection on the prevalence of the disease. A minor modification of












Figure 38. Scenario with an increased proportion of protected host and other datas of the Figure 33.
Figures 39-46 are plots of trajectories (Figure 39 and Figure 46), parametric curves (Figures 40-43) and respective finishing sections of trajectories in scenarios represented with parametric curves (Figure 44 and Figure 45), with the same initial states (three initial states) representing scenarios based on three protection strategies (poor protection indexed by










Figure 39. Scenario with a choice of a



modifying the proportion of host with in data of the scenario in Figure 39. It obviously appear how in all proportions, the level of the endemicity goes down.
6. Discussion on the Contribution
This paper stands as a mathematical contribution in order to evaluate how effective the utilization of bed nets in the fight against malaria in endemic areas can be. We proposed a model of the dynamic of malaria transmission involving a population of vectors and a population of humans as hosts subdivided into several sub-populations depending on the way they usually protect themselves against mosquito bites. Even though the model is made of a generic number of equations that can be high, the model is sufficiently simple to capture what is essential (i.e. how the protecting factors (





Figure 40. Scenario with a choice of a





and probabilities of the transmission from host to vectors
















Figure 41. Scenario with a choice of a





combination of parameters. If the highest proportion of hosts uses insecticide treated bed nets with good protection capability (i.e. if hosts use bed nets treated with insecticide with good repelling and killing capabilities), this acts on the level of the endemicity. As it appears in simulations in scenarios of more than three sub-populations of hosts, even though there are sub-populations that use low level protection, the impact of the high proportion of bed nets users that use well-protecting bed nets on the level of endemicity is obvious. The policy in countries in endemic area is founding the ownership of mosquitoes―treated net and advertising by various media for its large utilization by people. In Cameroon Mosquitoes―treated nets that are freely distributed are called MILDA (i.e. Moustiquaire Imprégnée à Longue Durée d’Action), meaning Bed Nets with long lasting protection against mosquitoes. Even though there is some doubt for its long lasting protective and killing capability, there is no concern regarding hypothetical regain of endemicity of the malaria. There is no




Figure 42. Scenario with a choice of a





need of changing old one for new one. The long lasting protecting capability of those Bed Nets can be also based on the fact of continuing of sleeping under the protection of a bed net, and the continuation of the policy of the distribution of “MILDA”.
An interesting research topic that can follow this paper is studying the regain of endemicity that can be observed, in certain malaria endemic regions. In the far north region of Cameroon, after the rainy season, months August to November 2013, there have been an increase on the level of endemicity of the malaria that have resulted in many deaths. A naive explanation of this fact can be the stopping of the utilization of bed net protecting measures associated with the profusion of the area by new hatching mosquitoes that happens with seasonal weather changes to dry to rainy and rainy to dry. People that have lost the immunity due to long term protection become totally susceptible and are exposed again.




Figure 43. Scenario with a choice of a





In simulations, we made a strong focus on scenarios of endemicity (i.e. scenarios with








Figure 44. Finishing sections of trajectories of infected host corresponding to parametric curves in Figure 40, Figure 41.
Finite Difference Scheme (NSFDS) has been used for the effectiveness of the shows. NSFDS is the scheme highly adapted for the integration of system with many equations like our models. Ode packages are less efficient (i.e. much longer processing time, and results with less accuracies).
7. Conclusion and Perspective
We have considered the problem of analyzing the model of the utilization of bed net in the fight against malaria. The proposed model takes into account multiple levels of protection with bed net in human population, multiple (questing, resting) steps between the first successful infected blood meal and the infectious state of mosquitoes. This consideration is a modeling of the activity of vectors in the dynamic of the malaria, which has not yet been




Figure 45. Finishing sections of trajectories of infected host corresponding to parametric curves in Figure 42, Figure 43.
considered by modelers of vectors borne diseases. As it appears in the analysis that we addressed, this can be a considerable step in the understanding of the complexity of vector borne diseases. We have obtained the basic reproduction number, whatever is the scale of the system; we have established that the DFE of the model is GAS providing that

African countries. A more realistic model must take into account parameters of death, birth and migration in human sub-populations, and the account must also be taken for exposed and removed states in human sub- populations. Our work seems non-negligible to us, since the endemicity of malaria happens by episodes, and in different episodes, values of parameters must not be the same. It is also the first time that the activity of vectors is used in the modeling of a vector borne disease.
Cite this paper
Jean ClaudeKamgang,Vivient CorneilleKamla,Stéphane YanickTchoumi, (2014) Modeling the Dynamics of Malaria Transmission with Bed Net Protection Perspective. Applied Mathematics,05,3156-3205. doi: 10.4236/am.2014.519298
References
- 1. WHO (2013) World Malaria Report 2013. Technical Report, WHO.
- 2. Gollin, D. and Zimmermann, C. (2007) Malaria: Disease Impacts and Long-Run Income Differences. IZA Discussion Papers 2997, Institution for the Study of Labor (IZA).
- 3. Ross, R. (1911) The Prevention of Malaria. John Murray, London.
- 4. Barbour, A.D. (1978) MacDonald’s Model and the Transmission of Bilharzia. Transactions of the Royal Society of Tropical Medicine and Hygiene, 72, 6-15.
http://dx.doi.org/10.1016/0035-9203(78)90290-0 - 5. Ngwa, A.G. and Shu, W.S. (2000) A Mathematical Model for Endemic Malaria with Variable Human and Mosqioto Population. Mathematical and Computer Modelling, 32, 747-763.
http://dx.doi.org/10.1016/S0895-7177(00)00169-2 - 6. Chitnis, N. (2005) Using Mathematical Models in Controlling the Spread of Malaria. Ph.D. Thesis, University of Arizona, Tucson.
- 7. Zongo, P. (2009) Modélisation mathématique de la dynamique de transmission du paludisme. Ph.D. Thesis, Universite de Ouagadougou, Ouagadougou.
- 8. Fontenille, D., Lochouarn, L., Diagne, N., Sokhna, C., Lemasson, J.J., Diatta, M., Konate, L., Faye, F., Rogier, C. and Trape, J.F. (1997) High Annual and Seasonal Variations in Malaria Transmission by Anophelines and Vector Species Composition in Dielmo, a Holoendemic Area in Senegal. American Journal of Tropical Medicine and Hygiene, 56, 247-253.
- 9. Rogier, C., Tall, A., Diagne, N., Fontenille, D., Spiegel, A. and Trape, J.F. (2000) Plasmodium falciparum Clinical Malaria: Lessons from Longitudinal Studies in Senegal. Parassitologia, 41, 255-259.
- 10. van den Driessche, P. and Watmough, J. (2002) Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Mathematical Biosciences, 180, 29-48.
http://dx.doi.org/10.1016/S0025-5564(02)00108-6 - 11. Carnevale, P. and Vincent, R. (2009) Les anophèles, Biologie, transmission du Paludisme et lutte antivectorielle. IRD.
- 12. Kamgang, J.C. and Sallet, G. (2008) Computation of Threshold Conditions for Epidemiological Models and Global Stability of the Disease Free Equilibrium. Mathematical Biosciences, 213, 1-12.
http://dx.doi.org/10.1016/j.mbs.2008.02.005 - 13. Bame, N., Bowong, S., Mbang, J., Sallet, G. and Tewa, J.J. (2008) Global Stability for SEIS Models with n Latent Classes. Mathematical Biosciences and Engineering, 5, 20-33.
http://dx.doi.org/10.3934/mbe.2008.5.20 - 14. Bowong, S. and Tewa, J.J. (2009) Mathematical Analysis of a Tuberculosis Model with Differential Infectivity. Communications in Nonlinear Science and Numerical Simulation, 14, 4010-4021.
http://dx.doi.org/10.1016/j.cnsns.2009.02.017 - 15. Perelson, A.S., Kirschner, D.E. and De Boer, R. (1993) Dynamics of HIV Infection of CD4+ T Cells. Mathematical Biosciences, 114, 81-125.
http://dx.doi.org/10.1016/0025-5564(93)90043-A - 16. Guo, H., Li, M.Y. and Shuai, Z. (2006) Global Stability of the Endemic Equilibrium of Multigroup Models. Canadian Applied Mathematics Quarterly, 14, 259-284.
- 17. Guo, H., Li, M.Y. and Shuai, Z. (2008) A Graph-Theoretic Approach to the Method of Global Lyapunov Functions. Proceedings of the American Mathematical Society, 136, 2793-2802.
http://dx.doi.org/10.1090/S0002-9939-08-09341-6 - 18. Korobeinikov, A. (2001) A Lyapunov Function for Leslie-Gower Predator-Prey Models. Applied Mathematics Letters, 14, 697-699.
http://dx.doi.org/10.1016/S0893-9659(01)80029-X - 19. Korobeinikov, A. (2004) Lyapunov Functions and Global Properties for SEIR and SEIS Models. Mathematical Medicine and Biology, 21, 75-83.
http://dx.doi.org/10.1093/imammb/21.2.75 - 20. Korobeinikov, A. and Maini, P.K. (2004) A Lyapunov Function and Global Properties for SIR and SEIR Epidemiological Models with Nonlinear Incidence. Mathematical Biosciences and Engineering, 1, 57-60.
http://dx.doi.org/10.3934/mbe.2004.1.57 - 21. Korobeinikov, A. and Wake, G.C. (2002) Lyapunov Functions and Global Stability for SIR, SIRS, and SIS Epidemiological Models. Applied Mathematics Letters, 15, 955-960.
http://dx.doi.org/10.1016/S0893-9659(02)00069-1 - 22. Ma, Z., Liu, J. and Li, J. (2003) Stability Analysis for Differential Infectivity Epidemic Models. Nonlinear Analysis: Real World Applications, 4, 841-856.
http://dx.doi.org/10.1016/S1468-1218(03)00019-1 - 23. McCluskey, C.C. (2006) Lyapunov Functions for Tuberculosis Models with Fast and Slow Progression. Mathematical Biosciences and Engineering, 3, 603-614.
http://dx.doi.org/10.3934/mbe.2006.3.603 - 24. McCluskey, C.C. (2003) A Model of HIV/AIDS with Staged Progression and Amelioration. Mathematical Biosciences, 181, 1-16.
http://dx.doi.org/10.1016/S0025-5564(02)00149-9 - 25. McCluskey, C.C. (2005) A Strategy for Constructing Lyapunov Functions for Non-Autonomous Linear Differential Equations. Linear Algebra and Its Applications, 409, 100-110.
http://dx.doi.org/10.1016/j.laa.2005.04.006 - 26. McCluskey, C.C. and van den Driessche, P. (2004) Global Analysis of Two Tuberculosis Models. Journal of Dynamics and Differential Equations, 16, 139-166.
http://dx.doi.org/10.1023/B:JODY.0000041283.66784.3e - 27. Tewa, J.J., Dimi, J.L. and Bowong, S. (2009) Lyapunov Functions for a Dengue Disease Transmission Model. Chaos, Solitons & Fractals, 39, 936-941.
http://dx.doi.org/10.1016/j.chaos.2007.01.069 - 28. Tewa, J.J., Fokouop, R., Mewoli, B. and Bowong, S. (2012) Mathematical Analysis of a General Class of Ordinary Differential Equations Coming from Within-Hosts Models of Malaria with Immune Effectors. Applied Mathematics and Computation, 218, 7347-7361.
http://dx.doi.org/10.1016/j.amc.2011.10.085 - 29. Bhatia, N.P. and Szegö, G.P. (1970) Stability Theory of Dynamical Systems. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-62006-5 - 30. LaSalle, J.P. (1968) Stability Theory for Ordinary Differential Equations. Stability Theory for Ordinary Differential Equations. Journal of Differential Equations, 41, 57-65.
http://dx.doi.org/10.1016/0022-0396(68)90048-X - 31. LaSalle, J.P. (1976) The Stability of Dynamical Systems. Society for Industrial and Applied Mathematics, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970432 - 32. LaSalle, J.P. (1976) Stability Theory and Invariance Principles. Dynamical Systems, Vol. I, Academic Press, New York, 211-222.
- 33. Anguelov, R., Dumont, Y., Lubuma, J. and Shillor, M. (2013) Dynamically Consistent Nonstandard Finite Difference Schemes for Epidemiological Models. Journal of Computational and Applied Mathematics, 255, 161-182.
http://dx.doi.org/10.1016/j.cam.2013.04.042 - 34. Kamgang, J.C. and Sallet, G. (2005) Global Asymptotic Stability for the Disease Free Equilibrium for Epidemiological Models. Comptes Rendus Mathematique, 341, 433-438.
http://dx.doi.org/10.1016/j.crma.2005.07.015 - 35. Berman, A. and Plemmons, R.J. (1994) Nonnegative Matrices in the Mathematical Sciences, Volume 9. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia.
- 36. Jacquez, J.A. and Simon, C.P. (1993) Qualitative Theory of Compartmental Systems. SIAM Review, 35, 43-79.
http://dx.doi.org/10.1137/1035003 - 37. Luenberger, D.G. (1979) Introduction to Dynamic Systems. Theory, Models, and Applications. John Wiley & Sons Ltd., Hoboken.
- 38. McCluskey, C.C. (2007) Global Stability for a Class of Mass Action Systems Allowing for Latency in Tuberculosis. Journal of Mathematical Analysis and Applications, 338, 518-535.
http://dx.doi.org/10.1016/j.jmaa.2007.05.012 - 39. Li, J., Blakeley, D. and Smith, R.J. (2011) The Failure of . Computational and Mathematical Methods in Medicine, 2011, Article ID: 527610.
http://dx.doi.org/10.1155/2011/527610
Appendix
A. Useful Definitions and Results
Herein, one finds definition of terms and notions used throughout the paper; some results, useful in our proof found here and there in the literature are also included; this in order to avoid frequent interruption of the exposition and to make the paper as self-contained as possible. The readers are pleased to refer to the cited reference for the proof of results.
Definition A.1 (Metzler matrix [35] -[37] ). A given

The qualification currently used to such matrix is the “



Definition A.2 (Irreducible matrix). A given


a matrix of permutation


where



Irreducibility of









Lemma A.1 (Arithmetic-Geometric Means Inequality[38] ).
Let

Furthermore, exact equality only occurs if
An immediate consequence of the Arithmetic-Geometric Means Inequality follows.
Corollary A.1 ([38] ). Let


Furthermore, exact equality only occurs if
Theorem A.1 ([12] ). Consider the system (5) defined on a positively invariant set
h1: The system is dissipative on
h2: The equilibrium




h3: The matrix


h4: There is an upper-bound matrix


trices




that

h5:
Then, the DFE


B. Proof of Proposition 3.4
Since the system reduced on the infection free sub-variety of








and



is Metzler stable matrix.


with





We make another iteration of the algorithm given by the proposition 3.3 above; we have:

stable if and only if




is a Metzler stable matrix.
with

For the last iteration of the algorithm, since

We have that the necessary and sufficient condition of the matrix

i.e.
with the expression of

this inequality is rewritten as
with the value of

After few algebraic arrangements in the above, we have

Thus the Matrix

We recall that


By biological means, the coefficient in the left of the condition (14) is the basic reproduction number. As a matter of fact, following the description in [6] of different factors that must be taken in account in the expressions of the basic reproduction number, we have the coefficient
that describes the successfulness for mosquitoes of crossing the



from the susceptible state to the infectious state is

gives the average number of secondary cases of mosquitoes which are infectious from primary infection within the contact with one infectious host of the

of [6] . Straightforwardly the average number of secondary cases of host of the


It comes out as it is usual while dealing with vector born diseases that
represents the average number of secondary cases of infectious vectors (respectively hosts) that are occasioned by one infectious vector (respectively host) introduced in a population of susceptible vectors (respectively hosts). i.e.




C. Proof of Proposition 3.5
The purpose of Proposition 3.5 is to determine possible steady states of the system (1).
The disease free equilibrium occur at a state




this is a linear equation which admits the unique solution

The endemic equilibriums would happen at probable states of the model




make components of the vector field that describe variations of infected and infectious components of the state of the model vanish.
The value of




substituting this value in the expression of

and thus,

For each




All components given above assume that there is a feasible non-zero


The first comes from the equality


The second comes from the expression of


and the two expressions depends on

Merging (15) and (16) gives the following equation with


Setting




made by the expression of (7), the expression (17) becomes:

Classically, at this stage, a rational function is derived; the property of the solution is obtained from the function in the numerator of the rational function, using the Descartes criterion that depends on the value of

Setting
we have that
















D. Non Standard Finite Difference Scheme Used in Simulations
The Non Standard Finite Difference Scheme uses for simulations is:

with


The time step function corresponding is

The equation above can be written in the short form as

where

The matrix

with




and






















 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,



 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,

































 ,
,
 ,
,
 ,
,
 ,
,



























