Journal of Global Positioning Systems (2002)
Vol. 1, No. 2: 85-95
GPS Attitude Determination Reliability Performance Improvement
Using Low Cost Receivers
Chaochao Wang and Gérard Lachapelle
Department of Geomatics Engineering, University of Calgary
Received: 13 October 2002 / Accepted: 4 December 2002
Abstract. This paper describes different methods to
improve reliability of attitude estimation using low cost
GPS receivers. Previous work has shown that low cost
receiver attitude determination systems are more
susceptible to measurement errors, such as multipath,
phase center offsets, and cycle slips. In some cases, these
error sources lead to severely erroneous attitude estimates
and/or to a lower availability. The reliability control in
the attitude determination becomes imperative to users, as
most attitude applications require a high level of
reliability.
The three methods tested herein to improve reliability are
the use of a high data rate, fixed angular constraints, and
a quality control algorithm implemented with a Kalman
filter. The use of high rate measurements improves error
detection as well as ambiguity fixing time. Fixed angular
constraints in a multi-antenna attitude system is effective
to reject incorrect solutions during the ambiguity
resolution phase of the process. Utilizing a Kalman filter
with a high data rate, e.g. 10 Hz, not only increases
reliability through an increase of information, but also
can improve accuracy and availability. The simultaneous
utilization of the above methods significantly improves
reliability, as demonstrated through a series of hardware
simulations and field tests. The low cost receiver type
selected is the CMC Allstar receiver equipped with a
commercially available low cost antenna.
Finally, the use of statistically reliability measures,
namely internal and external reliability measures, shows
the inherent limitations of a low cost system and the need
to either use better antennas and/or external aiding in the
form of low cost sensors.
Key words: GPS, Attitude Determination, Low Cost
Receiver
1 Introduction
Multi-antenna GPS systems provide a high accuracy
attitude solution without error drift over time [e.g., Lu
1994]. The performance of GPS attitude determination is
a function of receiver firmware, satellite geometry,
antenna carrier phase stability, multipath rejection ability
and inter-antenna distances. With advances in GPS
receiver technology, low cost receivers equipped with
phase lock loops that output precisely time-synchronized
carrier phase measurements are now available on the
market. The use of this grade of GPS receiver for attitude
determination has proven feasible [e.g., Hoyle et al.
2002]. However, it has been found that multipath,
antenna phase center offsets and cycle slips are major
error sources that mitigate the performance of low cost
receiver attitude solutions. In worst-case scenarios, these
errors severely affect the integrated carrier phase
measurements and lead to incorrect attitude estimates in
attitude determination. Therefore, the reliability of
attitude estimation becomes a major issue.
The objective of this paper is to investigate three
methodologies to improve the reliability performance of
attitude determination using low cost receivers. Three
different schemes, namely the use of high rate carrier
phase measurements, fixed angular constraints and a
Kalman filter with a statistical quality control system, are
used interactively to improve reliability. These schemes
are implemented in a high performance, open architecture
attitude determination software, namely HEADRT+TM,
for testing [e.g. Hoyle et al 2002]. The performances of
different methods are examined both in hardware
simulation mode and under field static and kinematic
conditions.

86 Journal of Global Positioning Systems
2 GPS Attitude Determination Because of the short inter-antenna distance (generally less
than 20 m), the spatially correlated orbital and
atmospheric errors virtually cancel out from the equation.
The errors sources remaining here are only multipath,
antenna phase center offsets and carrier receiver noise,
provided that the double difference integer ambiguities
are correctly solved.
By definition, attitude is the rotation of a specific frame
with respect to a reference frame, which is well defined in
space. In the case of a multi-antenna system, this specific
frame is usually referred to as the antenna body frame,
while the local level frame is selected as the reference
frame. Once the antenna vector in the local level frame is
precisely determined, the three Euler attitude angles in
the rotation matrix can be estimated using Equation 1. 3 Reliability Problems Using Low Cost Receivers










=










ll
ll
ll
b
b
b
z
y
x
hRpRrR
z
y
x
)()()( 312 (1)
where
h, p, r denote heading, pitch and roll
x, y, z are the coordinates of the antenna vector
superscript b represents the body frame
superscript ll stands for the local level frame
The GPS receivers determine the inter-antenna vectors
firstly in a Conventional Terrestrial frame, namely WGS-
84. The carrier phase measurements have to be used as
observables in this application since the attitude
determination system requires high precision relative
positioning between the antennas. In the general case that
independent (non-dedicated} receivers are used and each
receiver has a separate oscillator, the double differencing
combinations are formed so that not only the clock errors
but also the line biases caused by the different cable
lengths can be removed. Without clock and line bias
errors, the carrier phase double difference observation
equation is expressed as
tropion dddN ∆∇+∆∇−∆∇+∆∇+∆∇=∆Φ∇
ρλρ
rxmulti
εε ∆∇+∆∇+ ant ε ∆∇+ (2)
Previous research has shown the advantages and
limitations of using low cost receivers such as the CMC
Electronic Allstar, for attitude determination [e.g, Hoyle
et al 2002]. Without multipath and antenna impact, this
receiver type can achieve attitude estimation performance
comparable with high quality/high cost units during
hardware simulation testing. This is because, under
hardware simulation conditions, error sources can be
separated. No multipath or antenna phase centre errors
need to be introduced, thereby allowing a performance
analysis of the receiver noise and tracking loops. Under
field conditions, the low cost receiver is more likely to
suffer from carrier phase multipath and antenna phase
instabilities. In practice each of these two error sources
range from a few mm to 1 cm (although higher values are
possible). In some severe cases, the two error sources,
coupled with cycle slips, significantly deteriorate the
carrier phase measurements and the wrong double
difference ambiguities could be produced from the
ambiguity resolution. The incorrect ambiguities
eventually lead to the erroneous attitude estimates, which
impair the reliability of the whole attitude determination
system. In order to improve the overall attitude
performance, some measures should be taken to enhance
the reliability of attitude determination using low cost
receivers.
4 Attitude Determination Algorithm
where:
∆∇ represents the double difference operator In the HEADRT+TM software, the attitude determination
estimation process is carried out in two phases. The first
phase determines the correct double difference carrier
phase ambiguities for the antenna vector(s). After the
coordinate transformation from WGS-84 into the local
level frame, the attitude parameters are estimated from
the vector components with corresponding variance-
covariance matrix in the second phase [e.g. Lu 1994].
∆Φ∇ is the double difference carrier phase
measurement
ρ ∆∇ is the double difference range
N∆∇ is the double difference integer ambiguity
λ is the carrier wavelength (m)
ρ
d∆∇ is the orbital error
tropion dd ∆∇∆∇ , are the errors due to the ionospheric
delay and tropospheric delay The ambiguity resolution used in the software is based on
the Least Squares Ambiguity Search Technique (LSAST)
[Hatch 1991]. This method has the advantages of a small
number of candidate ambiguity combinations and high
computational efficiency. Given that the vector lengths
are small, this technique is effective for this purpose. The
ambiguity search region is defined as a sphere with the
multi
ε ∆∇ is the double difference multipath error
rx
ε ∆∇ is the double difference carrier phase error due
to the receiver noise
ant
ε ∆∇ is the double difference antenna phase center
offset

Wang and Lachapelle: GPS Attitude Determination Using Low Cost Receivers 87
radius of the inter-antenna distance(s). After forming all
possible ambiguity combinations, different discrimination
tests are conducted to isolate the correct ambiguity set
using the fixed antenna distance(s) and some other
statistical properties [e.g., Hoyle et al. 2002]. Two
statistical tests are involved in the ambiguity resolution,
namely the ratio test and the Chi-square test. The
underlying assumption of a ratio test is that the residuals
of the correct ambiguities should be significantly smaller
than those of the incorrect ones. Only if the ratio of the
two smallest residual quadratic forms is greater than a
preset threshold (normally 2.5 to 4), is the potential
ambiguity set with the smallest quadratic form accepted
as the correct ambiguity set. For true ambiguities, it is
assumed that the double difference residuals are normally
distributed, and the sum of the quadratic forms follows
the Chi-square distribution, with the degree of freedom
being the redundant measurement number. Therefore, a
Chi-square test based on the residuals is conducted to
verify the double difference ambiguities in the software.
Once the inter-antenna vector ambiguities are fixed, the
inter-antenna vector components are transformed from
WGS-84 earth-fixed frame into local level coordinates
and the attitude parameters are computed from an implicit
least squares estimation. Currently, no dynamic
constraints of the platforms are implemented in the
filtering process to permit an epoch-by-epoch assessment
of attitude estimation under any dynamics, subject to the
availability of unbiased receiver carrier phase).
5 High Data Rate
As the CMC Allstar receiver can output raw time
synchronized carrier phase measurements up to 10 Hz, it
allows for high data rate processing in HEADRT+TM,
both for ambiguity resolution and attitude estimation. The
higher data rate can benefit the ambiguity resolution
process due to the high availability of phase
measurements. Also, platform dynamics can be predicted
for short time intervals in many applications and outlier
estimation in the antenna vector lengths can be easily
detected and further rejected using filtering of the high
rate measurements. In this section, only the effect of the
high data rate on ambiguity resolution will be
investigated. The impact of the high data rate on Kalman
filter estimation will be discussed in the sequel.
In order to evaluate the performance of ambiguity
resolution, the time to fixed ambiguities is utilized. In this
test, two receivers were used, both for the hardware
simulator and field test. In the latter case, two AT575-104
low cost antennas were used. The hardware simulation
test was done using a Spirent STR-4760 simulator. As no
errors were simulated, the only remaining error present
was receiver measurement noise. The field test was
conducted on the roof of Engineering building at the
University of Calgary. The inter-antenna distances were
about 1 m in both tests. The data was collected at a 10-Hz
rate. The double difference ambiguities were intentionally
reset every 120 seconds during the data processing to
gather enough trials for a meaningful analysis. The
Minimum Time To Ambiguity Fix (MTTAF) was set to 1
epoch and the fixing ratio was set to 3 in HEADRT+TM.
0
20
40
60
80
100
<0.1<1<5<10 <20>20
Ambiguity Fixing Time(Seconds)
Percentage(%)
0
20
40
60
80
100
Cumulative
Percent(%)
10Hz Data1Hz Data
Fig. 1 Time to Fix Ambiguity in hardware simulation
Fig. 1 shows the ambiguity fixing times for the case of
the hardware simulation test. Without multipath and
antenna phase center offset, the integer ambiguities were
successfully determined within a single epoch (1s or 0.1
s) during each trial, demonstrating that the CMC receiver
measurement noise is not a significant factor that is
affecting ambiguity resolution performance.
0
20
40
60
80
100
<1<5<10<60<120 >120
Ambiguity Fixing Time(Seconds)
Percentage(%)
0
20
40
60
80
100
Cumulative
Percent(%)
10Hz Data1Hz Data
Fig. 2 Time to Fix Ambiguity in static field test
The corresponding static field test statistics are shown in
Fig. 2. With the existence of multipath and antenna phase
center errors, 19.6 % of the ambiguities were fixed in one
second with 1 Hz data. The integer ambiguities were
fixed in 5 seconds 84.9 % of the time. Meanwhile, with
10 Hz measurement rate, the corresponding values were
89.4 % and 93.4 % respectively. The time required to fix
the ambiguity could be significantly reduced using high
data rate in this case during some trials. However, there
are cases where the fixing time was larger than 60
second. This was related to the presence of time-
correlated multipath and antenna phase center offset
errors. The high data measurement is less effective to
these errors.
Tab. 1 shows that the probability of resolving correct
ambiguities for the field test is 93% for 1 Hz data and

88 Journal of Global Positioning Systems
96% for 10 Hz data. With the higher rate measurements,
the ambiguity resolution reliability can thus be only
slightly improved. Even though the incorrect ambiguities
were selected occasionally, they can be easily rejected in
the attitude software either by improving the MTTAF
parameter in ambiguity resolution or by the reliability
control in the attitude estimation phase.
Then, the estimated angle is compared with the
known angle . If the ambiguities of two inter-antenna
vectors are correctly solved, the two angles should be
consistent within a certain tolerance.
E
θ
θ
δθθ <− E (4)
Tab. 1 Performance of ambiguity resolution using different data rate
measurements The numerical value of the angular tolerance in (4)
depends on the inter-antenna distance and the quality of
phase measurements, which are a function of
measurement noise, multipath and phase centre stability.
In the case of antenna vector lengths of 1-2 m and a
moderate carrier phase measurement quality, a 5-degree
tolerance is appropriate to detect the wrong ambiguities.
If at least four antennas are used in the attitude
determination system and only one vector ambiguity is
wrong, this erroneous ambiguity combination can be
detected and identified by checking all the angles
between the inter antenna vectors.
δ
Correctness (%) 10 Hz data 1 Hz data
Simulation Test 100% 100%
Static Field Test 96 93
6 Fixed Angular Constraint Scheme
If one can assume that the antennas are mounted on a
rigid platform, then their relative positions are fixed
regardless of the platform motion. The full antenna frame
geometry is known a priori and appropriate constraints
can be used in the ambiguity resolution process to take
advantage of this knowledge. Many geometric constraints
have been brought forward for the ambiguity resolution
in multi-antenna GPS attitude determination system. [El-
Mowafy 1994, Euler and Hill 1995] In this research, the
fixed angle between the antenna vectors, as well as the
vector length, was employed to verify the double
difference ambiguities.
A hardware simulation test was conducted with the 4760
simulator to investigate the validity of the angular
constraint scheme. An antenna body frame was simulated
using inter-antenna distances of 1 m. The angles between
the antenna vectors were intentionally set to 90 degrees in
this test. The initial parameters used in the software were
• Fixing ratio =3
• MTTAF =1 epoch
The implementation of the angular constraint is
straightforward. First, the fixed planar angles ()
between antenna vector pairs could either be measured a
priori or calculated using the antenna coordinates in the
body frame. Once the integer ambiguities of the antenna
vector pairs have been determined, the angle between the
pairs can be directly computed using the antenna vector
coordinates in the local level frame:
θ
LL
AC
LL
AB
LL
AC
LL
AB E
bb
bb v
r
rr
⋅
⋅
=−1 cos θ
ACAB
LL
AC
LL
AB
LL
AC
LL
AB
LL
AC
LL
AB
bb
VVNNEE
⋅
∆∆+∆∆+∆∆
=−1 cos (3)
where
E
θ
is the estimated angle between the two antenna
vectors
Fig. 3 DOPs and SV number during simulator test
Fig. 3 shows the satellite’s azimuth and elevation DOPs
during the test. At GPS time 216932 s, the loss of SV27
signal in one of the secondary receivers caused the failure
of the Chi-square test and the re-initialization of the
double difference ambiguity for the corresponding inter-
antenna vector. Unfortunately, the wrong ambiguity was
determined due to the short MTTAF. When SV27 was re-
acquired by the receiver, an incorrect ambiguity was first
LL
AC
LL
AB bb
rr
, are the antenna vectors in local level frame
ACABbb, are the lengths of the antenna vectors
VNE ∆∆∆ ,, are three components of antenna vector
in east, north, and vertical directions
subscripts represent the primary antenna and
two secondary antennas
CBA ,,

Wang and Lachapelle: GPS Attitude Determination Using Low Cost Receivers 89
found, with the true ambiguity obtained afterwards. The
effect of this error on the inter-antenna vector solutions
during this period is shown in Fig. 4. The inter-antenna
length components are obviously incorrect. However, the
length itself was corrected solved and testing of the
solution with that known length failed to detect the
incorrect solution in this case.
Fig. 4 Effects of an incorrect ambiguity on an inter-antenna vector
estimate
Since no quality control procedure was performed in the
least squares attitude estimation, the erroneous inter-
antenna vector solutions inevitably led to the wrong
attitude parameters. The error effects on the attitude
component estimates are shown in Fig. 5.
Fig. 5 Effects of an incorrect ambiguity on attitude component
estimates
After the angular constraint scheme was implemented in
the software, the wrong ambiguity was easily detected
and the erroneous vector solution was successfully
detected and excluded from the attitude estimation. As
shown in Fig. 6, the correct attitude components were
estimated in the least squares solution using the other two
inter-antenna vectors. The small shift in the attitude
estimates is due to the exclusion of SV27 and the
resulting slight change of satellite geometry. The mean
and rms agreements in heading, pitch and roll are 2.1, 0.3,
-0.2, 2.8, 3.4 and 3.3 arcmins, respectively.
Fig. 6 Attitude results after implementing angular constraints in static
simulation test
By employing the angle consistency check in the
ambiguity resolution, some incorrect ambiguity solutions
can be effectively rejected, which significantly improves
the reliability of multi-antenna attitude determination.
7 Kalman Filter Estimation
Kalman filtering estimation provides a recursive method
for the determination of attitude components through a
predicting and updating process. The general formulas in
Kalman filtering can be written as [Brown & Hwang
1992]
kkkk vxHz +⋅= (5)
kkkk wxx +⋅= −1
φ (6)
where
k
z is the measurement vector at time k
k
H is the design matrix
k
x is state vector at time k
k
v is the measurement noise with covariance R
k
φ is the transition matrix
k
w is the process noise with covariance Q
In attitude determination using vector components, the
“measurements” are the antenna vector components in the
local level frame. The design matrix is the partial
derivative of the rotation matrix with respect to the state
vector in Equation 1.

90 Journal of Global Positioning Systems
x
R
H∂
∂
= (7)
The state vector here includes the three Euler attitude
parameters and their angular rates:
(
T
x ϕθψϕθψ
&
&
&
= )
(8)
The transition matrix and the process noise can be
expressed as follows
φ




















=
100000
010000
001000
00100
00010
00001
dt
dt
dt
φ
(9)




















=
2
2
2
00000
00000
00000
000000
000000
000000
ϕ
θ
ψ
σ
σ
σ
&
&
&
Q
(10)
α
The numerical values of the angular rate variances in (10)
represent the tightness of the dynamic constraint of the
Kalman filter. In vehicular attitude determination, the
sigma of the angular rate in the Q matrix is empirically
selected as 2 degrees per epoch in 10 Hz sampling in the
present case. Intuitively, one realizes that the
effectiveness of the filter in detecting incorrect solutions,
thus improving reliability, will depend on our a priori
knowledge of the vehicle dynamic and of the
measurement rate.
Using this model, the attitude parameters and their
angular rates can be correctly estimated in the Kalman
filter as long as all the measurements are free of errors.
As previously mentioned, the measurements used in the
Kalman filter are the inter-antenna vector solutions after
ambiguity resolution. In the case that the wrong
ambiguity is determined, these “quasi-measurements” are
in error and the attitude estimates calculated from the
Kalman filter may deviate from the truth. In order to
reject the incorrect inter-antenna vector solutions from
the Kalman filter and improve the reliability of the
attitude estimates, a quality control system based on the
filter innovation sequences is introduced herein.
The innovation sequence is the difference between the
actual system output and the predicted output based on
the predicted state (see Equation 11) [Teunissen &
Salzman 1988].
)(−− −=kkk xfzv)
(11)
Under normal conditions, the innovation sequence is a
zero-mean Gaussian white noise sequence with known
variance. In the presence of erroneous measurements,
such assumptions are no longer valid, and the innovation
sequence deviates from its zero mean and white noise
properties. Thus some statistical tests can be conducted to
detect and identify outliers or faults in the measurements.
Firstly, an overall model test is conducted to detect the
errors in the measurement vector. The test statistics in
this global test are given as
)0,(~ 21 mvCvT ak
v
T
kk k
χ
−−−
−
= (12)
where
m is the number of observations taken at time , k
−
k
v
C is the covariance matrix of the innovation and
2
α
χ
is the Chi-square probability with a significance
level of .
If the global test is rejected, the system error can be
identified with the one-dimensional local slippage test.
)1,0(~
1
1
Ν= −
−−
−
−
i
v
T
i
k
v
T
i
ik lCl
vCl
w
k
k (13)
where
T
i
i
i
i
l)0,...,0,1,0,...0(11 +− = for =1,…,m i
The significant level in the local test is suggested to be
0.999, which leads to a boundary value of 3.29. Thus the
i-th measurement is flagged for rejection when
α
29.3>
i
w (14)
When implementing statistical tests to identify outliers in
the measurements, two types of errors may be made, as
shown in Fig. 7. The first type (Type I) is rejecting a
good measurement. The probability associated with this
type error is denoted by . If a bad measurement is
accepted by the test, a Type II error occurs. The
probability of a Type II error is expressed as .
α
β
Fig. 7 Type I/II Errors
Given the probability values of Type I and Type II errors,
the Minimum Detectable Blunder (MDB) can be
calculated as the ability to detect errors in the system as

Wang and Lachapelle: GPS Attitude Determination Using Low Cost Receivers 91
i
v
T
i
ilCl
z
k
1
0
−
−
=∇
δ
(15)
where is a function of and (see Fig. 8).
0
δα β
In GPS kinematic applications, and are commonly
selected to be 0.001 and 0.2 respectively and is then
4.13.
α
β
0
δ
In the presence of strong multipath, the identification test
(Equation 15) may be too sensitive and will sometimes
lead to a false alarm. In order to alleviate this problem, a
further step was introduced by comparing the innovations
with the MDB. If the innovation is larger than the MDB,
the measurement is identified erroneous, otherwise it is
considered a false alarm.
The modified Kalman-filter-based attitude determination
software was tested with the data collected with the
Spirent 4760 hardware simulator using four CMC
receivers. A vehicle trajectory was simulated in this test
and the antenna configuration is shown in Figure 8. The
maximum attitude changes were about 20 degree/s in
heading and several degrees per second in pitch. The true
attitude during the test is plotted in Fig. 9.
Fig. 8 Simulated vehicle test antenna configuration
Fig. 9 True attitude parameters during hardware simulator test
The results, summarized in Fig. 10 and Table 2, show
that the Kalman filter method did not work well with
tight dynamic constraints using a 1-Hz date rate, as over
shooting effects occur. With a 10-Hz data rate, the
performance of the filter is excellent, the attitude
parameter estimates being slightly better than those of the
least squares estimates.
Fig. 10 Attitude estimate errors using different estimation methods
Tab. 2 RMS – Kalman filter versus least-squares
RMS Heading Pitch Roll
10 Hz LS 3.9’ 11.8’ 9.9’
10 Hz KF 3.9 9.8 7.9
1 Hz KF1 31.9 11.8 9.0
In order to test the performance of cycle slip detection
using the quality control method implemented by the
Kalman filter, 80 cycle slips were introduced in the
carrier phase measurements on different receivers with a
magnitude ranging from 1 to 8 cycles. Using the
traditional phase prediction detection and inter-antenna
length consistency check, all the cycle slips but one were
either detected or recovered. The remaining cycle slip
was removed when the Kalman filter was used, as shown
in Fig. 12.
Fig. 11 Cycle slip detection using Kalman filter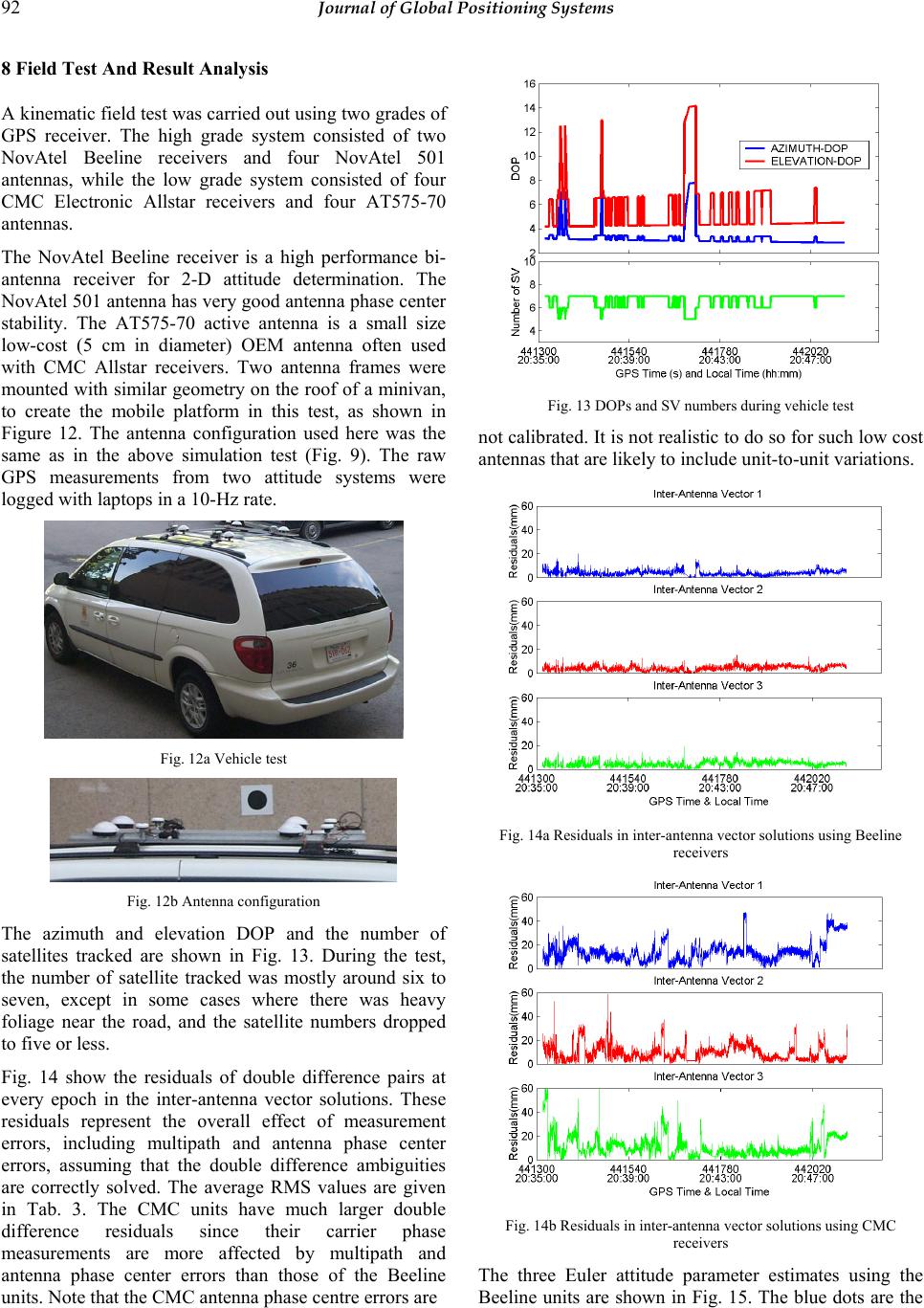

92 Journal of Global Positioning Systems
8 Field Test And Result Analysis
A kinematic field test was carried out using two grades of
GPS receiver. The high grade system consisted of two
NovAtel Beeline receivers and four NovAtel 501
antennas, while the low grade system consisted of four
CMC Electronic Allstar receivers and four AT575-70
antennas.
The NovAtel Beeline receiver is a high performance bi-
antenna receiver for 2-D attitude determination. The
NovAtel 501 antenna has very good antenna phase center
stability. The AT575-70 active antenna is a small size
low-cost (5 cm in diameter) OEM antenna often used
with CMC Allstar receivers. Two antenna frames were
mounted with similar geometry on the roof of a minivan,
to create the mobile platform in this test, as shown in
Figure 12. The antenna configuration used here was the
same as in the above simulation test (Fig. 9). The raw
GPS measurements from two attitude systems were
logged with laptops in a 10-Hz rate.
Fig. 13 DOPs and SV numbers during vehicle test
not calibrated. It is not realistic to do so for such low cost
antennas that are likely to include unit-to-unit variations.
Fig. 12a Vehicle test
Fig. 14a Residuals in inter-antenna vector solutions using Beeline
receivers
Fig. 12b Antenna configuration
The azimuth and elevation DOP and the number of
satellites tracked are shown in Fig. 13. During the test,
the number of satellite tracked was mostly around six to
seven, except in some cases where there was heavy
foliage near the road, and the satellite numbers dropped
to five or less.
Fig. 14 show the residuals of double difference pairs at
every epoch in the inter-antenna vector solutions. These
residuals represent the overall effect of measurement
errors, including multipath and antenna phase center
errors, assuming that the double difference ambiguities
are correctly solved. The average RMS values are given
in Tab. 3. The CMC units have much larger double
difference residuals since their carrier phase
measurements are more affected by multipath and
antenna phase center errors than those of the Beeline
units. Note that the CMC antenna phase centre errors are
Fig. 14b Residuals in inter-antenna vector solutions using CMC
receivers
The three Euler attitude parameter estimates using the
Beeline units are shown in Fig. 15. The blue dots are the

Wang and Lachapelle: GPS Attitude Determination Using Low Cost Receivers 93
least squares attitude estimates and their 3-sigma standard
deviation envelopes, while the red dots are the
corresponding estimates from the Kalman filter with the
quality control method turned on.
Tab. 3 Residuals RMS (mm) for Beeline and CMC receivers
Inter-antenna
Vector
Beeline Rcvrs CMC Rcvrs
1 5 17
2 5 12
3 5 15
Fig. 15 Attitude estimates using the Beeline system
Using least squares estimation, wrong attitude parameter
estimates were output when heavy satellite blockages
occurred. The reason for this is that the least squares
estimation was severely affected by incorrect vector
solutions in such circumstances. Once the base satellite is
lost, the double difference ambiguities have to be
resolved at the next epoch. As is known, ambiguity
resolution performance is highly correlated to the number
of visible satellites and their geometry. In a heavy signal
blockage area with strong multipath and phase center
variations, ambiguity resolution is more likely to result in
an incorrect solution, which leads to erroneous attitude
parameter estimates. These incorrect estimates can
however be easily identified by inspecting the 3-sigma
standard deviation envelopes.
Once a Kalman filtering with the quality control method
and the angular constraints are implemented, the wrong
inter-antenna vector solutions are detected and excluded
from the solution. This eliminates erroneous attitude
parameters from the output. The Kalman filter 3-sigma
standard deviation envelopes are slightly smaller than
those from the least squares method due to the filter
constraints. As can be seen in the figures, the standard
deviation improvement is more significant in pitch and
roll than in heading. This is because the pitch and roll
dynamics were lower than those of heading.
Fig. 16 Attitude estimates using the CMC system
The attitude results from the CMC units are shown in Fig.
16. The overall attitude estimation accuracy was slightly
lower than that obtained with the Beeline units. Using the
Kalman filter augmented with the quality method,
erroneous vector solutions, which caused wrong attitude
estimates in the least squares approach, were successfully
identified and rejected from the attitude estimation. As
the phase measurements from CMC units are more
vulnerable to multipath, phase center errors and cycle

94 Journal of Global Positioning Systems
slips, erroneous inter-antenna vector solutions were more
frequently determined. When more incorrect solutions
were rejected by the Kalman filter, the availability of
attitude estimates degraded due to the reduction of correct
“quasi-observables” compared with the result from the
least squares method. The lowered number of vector
solutions involved in attitude estimation, coupled with the
larger carrier phase errors, caused large variations in the
estimation accuracy of the Kalman filter.
The estimated attitude differences between the Beeline
and CMC systems are shown in Fig. 17, and the
corresponding statistics are summarized in Table 4. The
estimated differences are mostly within 1.5 degrees in
heading and 3 degrees in pitch and roll. The largest
differences occur during periods of poor satellite
geometry.
Fig. 17 Attitude differences between the Beeline and CMC systems
Tab. 4 Statistics of attitude difference between Beeline and CMC units
(Units: degrees
Difference Heading Pitch Roll
Mean 0.68 -
0.74
-
0.24
RMS 0.94 2.26 2.17
Max(abs) 4.56 8.64 9.44
Figure 18 shows the external statistical reliability of the
two systems. External reliability is the impact of the
maximum measurement errors that could occur and go
undetected, on the attitude estimates, for two systems.
This reliability measure is a function of the quality of
carrier phase measurements and of the redundancy
numbers in the Kalman filters. The external reliability of
the Beeline system is fairly consistent during the test
except during times of poor geometry. The corresponding
reliability of the CMC system is much poorer due to the
higher multipath and antenna phase center errors. It is
important to note that the estimated attitude differences in
Figure 23 are within the reliability numbers of Figure 24
and 25. Thus, one can conclude that the CMC units have
reached their limit in term of accuracy performance, if
one assumes that the choice of antennas is limited to
current low cost units. In order to increase attitude
component estimation performance, higher performance,
but more expensive antennas could be used. The use of
long inter-antenna distances would also improve
accuracy. Aiding with external sensors is the other
alternative.
Fig. 18 External reliability
9 Conclusions
Multipath, cycle slips and antenna phase center instability
are major error sources limiting the reliability of
standalone GPS-based attitude determination with low
cost receivers. Even if a required level of accuracy can be
achieved with a given multiple receiver configuration,
reliability becomes a major issue. It has been
demonstrated herein that the use of angular constraints
and a Kalman filter with a high data rate are effective to
significantly improve reliability. However, the use of
statistical reliability analysis has also shown the
limitations of the above techniques.
Another technique is currently being assessed to improve
reliability and error detection, namely the use of low cost
rate gyros integrated with the antenna assembly in
various configurations. Given a GPS data rate of 10 Hz,
such low cost rate gyro should still be useful for short
term prediction between the GPS measurements,
smoothing, error detection and enhancement of
availability. Early results indicate these are possible
enhancements indeed.

Wang and Lachapelle: GPS Attitude Determination Using Low Cost Receivers 95
References
Brown, R.G. and P.Y.C. Hwang (1992) Introduction of
Random Signals and Applied Kalman Filter, Second
Edition, John Wiley & Sons, Inc., New York
El-Mowafy, A, (1994) Kinematic Attitude Determination
From GPS, Ph.D dissertation, UCGE Reports 20074,
University of Calgary, Calgary, Alberta, Canada, 1994
Euler H.-J. and Hill C.D., (1995) Attitude Determination:
Exploiting All Information for Optimal Ambiguity
Resolution, Proceedings of the ION GPS-95, Palm
Springs, CA, September, 1995
Hatch, R. (1991) Instantaneous Ambiguity Resolution,
Proceedings of the IAG International Symposium 107 on
Kinematic Systems in Geodesy, Surveying and Remote
Sensing, Banff, Canada, September, 1990, Springer-
Verlag, New York.
Hoyle, V., Lachapelle, G., M.E. Cannon and Wang, C. (2002)
Low-Cost GPS Receivers and their Feasibility for
Attitude Determination, Proceeding of NTM02, The
Institute of Navigation, San Diego, CA, pp. 226-234
[http://www.geomatics.ucalgary.ca/research/GPSRes
earch/first.html]
Lu, G. (1994) Development of a GPS Multi-Antenna System
for Attitude Determination, Ph.D thesis, Report No.
20073, Department of Geomatics Engineering, University
of Calgary [http://www.geomatics.ucalgary.ca/links/
GradTheses.html]
Teunissen, P.J.G. and Salzman, M.A. (1988) Performance
Analysis of Kalman Filters, Report of the Faculty of
Geodesy, Delft University of Technology, Delft, The
Netherlands.