Theoretical Economics Letters
Vol. 2 No. 3 (2012) , Article ID: 21504 , 6 pages DOI:10.4236/tel.2012.23063
Economic Station-Centered Network and Invisible Collaboration: A Cyclic vs Semi-Cyclic View
1Kanagawa University, Yokohama, Japan
2University of Electro-Communications, Tokyo, Japan
Email: matsui@kanagawa-u.ac.jp, matsui@se.uec.ac.jp
Received April 12, 2012; revised May 15, 2012; accepted June 16, 2012
Keywords: Economics/Reliability; Ellipse Theory; Demand Speed (Invisible Hand); Station-Centered Approach; Economic Balancing; Parallel Type Collaboration
ABSTRACT
By our past review, this paper will verify the hypothesis that the autonomous (invisible) body balancing would be better under changeable demand speed and a leading principle in the collaborative networks. This hypothesis was first utilized in the Conveyor-Serviced Production System (CSP System) with cycle time by a Station-Centered Approach to the physical networks. Recently, we are ascertaining this hypothesis in cost/profit balancing under demand speed (invisible hand) at the economic body chain networks. Generally, it becomes simpler at series (cyclic) type, but would not be so at parallel (semi-cyclic) type. Throughout this paper, we will point out the principle of autonomous (invisible) body balancing by demand speed (cycle time), and would extend to a parallel (semi-cyclic) supply chain by the Station-Centered Approach. This thing would bring the invisible merit that the profit maximization occurs at the relative cost balancing of each enterprise in a series-parallel body network.
1. Introduction
From Reis et al. [1], the station-centered approach has first been used to Conveyor-Serviced Production Systems (CSP System) in Matsui [2-4]. This is superior to the system-centered approach (Hunt [5]) in terms of treating the detailed (or practical) model and designing each station buffer in networks (Matsui [4,6]). This contrast is seen in Aumanu [7].
Recently, this approach has been extended to treat the not only physical but also cost/profit performance and balancing issues (Matsui [8-10], Yamada and Matsui [11]). In this cyclic case, the product form of production rates becomes easy to the sum form of each performance of stations.
This paper would show to be able to apply this approach to visualize the invisible hand in network collaborations (Matsui & Ichihara [12], Matsui [10]). We will develop the hypothesis that each unit-optimization in profit gives in the total optimization in sum and this results in the non-cooperative solution.
This hypothesis is able to be visualized by the ellipse theory that the profit maximization is attainable at the optimal demand speed (Matsui [10]), and then, the relativecost/profit balancing is obtained in the near point (Matsui [13]). For the reliability, this ellipse shape intersects the ellipse shape in lead-/busy-time.
Recently, we are ascertaining this hypothesis in cost/ profit balancing under demand speed (invisible hand) at the economic body chain networks. Generally, it becomes simpler at series type, but would not be so at parallel type (Matsui and Dai [14]). Throughout this paper, we will ascertain the principle of autonomous (invisible) body balancing by demand speed (cycle time), and would extend to a parallel supply chain by the Station-Centered Approach at the point of semi-cyclic view.
Similar to Matsui [13], this thing would bring the invisible merit that the profit maximization occurs at the relative cost balancing of each enterprise in a series-parallel body network. Note that this balancing issues would be near to and recalled at non-equilibrium in analog.
The organization of the paper is as follows:
First, the station-centered approach is physically outlined. Next, this is developed to an economic world.
Finally, a class of enterprises network is discussed in visible collaboration.
2. Outline of Station-Centered Approach
2.1. Two Approaches to CSP System
A typical example of station-centered approach (SCA) to network problem is seen in the conveyor system with cyclic flow, and is called the CSPS System (see Figure 1). This CSP System is a class of queueing networks with lost units, and is one of complex and intractable queueing systems.
The CSP System (i) does not necessarily correspond to a queueing system of tandem type, since blocking does not occur in the sense that arriving units overflow when an operator is busy, and thus, is studied as the cyclic type (series system) by industrial practice or computer simulation. Only non-mechanical (or non-paced) lines may be treated as the queueing system of tandem type. Also, the CSP System (ii) may be treated as the semi-cyclic type (a multichannel queueing system with ordered entry), but the distance between stations and the detailed activity of each operator are neglected.
The traditional approach to CSP System is classified in the two types below. Such a treatment as the queueing system with ordered-entry or of tandem type is especially called the system-centered approach. The treatment that decomposes CSP System to each independent station (queueing sub-system) is called the station-centered approach. The treatment that decomposes CSP System to each independent station (queueing sub-system) is called the station-centered approach. One of the queueing subsystems for the case of fixed items is a moving-operator without delay, while the Conveyor-Serviced Production Station (CSPS) is a typical queueing sub-system for the case of removal items with delay.
The station-centered approach is superior the systemcentered approach in terms of treating the detailed (or practical) model and designing each station buffer of CSP System, but it is lacking of the basic theory that decomposes or synthesizes each queueing sub-system and designs the totally optimal CSP System. This reason results in the fact that the property of departure or overflow processed is not simple except the type of M/M/s, and thus, is an obstacle to the smooth development of conveyor theory.
2.2. Network Flow and Balancing
The mean input interval time is a design (or decision) variable of the coordinator, and is denoted by  . The production rate,
. The production rate,  , is defined as an inverse of the mean inter-departure time, i.e., mean time between successive departures. The overflow rate,
, is defined as an inverse of the mean inter-departure time, i.e., mean time between successive departures. The overflow rate,  , is defined as an inverse of mean inter-overflow time, i.e., mean time between successive overflows.
, is defined as an inverse of mean inter-overflow time, i.e., mean time between successive overflows.
In the Models I and II, the following relation is generally satisfied:
 (2.1)
(2.1)
A practical assumption for CSP System is here introduced to produce the production quantity required in the planning period. This thing is easy, if it is able to approach the inter-departure time to the input interval time, and is realized by providing the enough large buffers within stations. Then, the followings may be useful:
 (2.2)
(2.2)
Under this assumption, the input interval time, d, is called the cycle time. An estimated value of ,
, 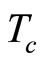 , is obtained from the planning period divided by the production quantity.
, is obtained from the planning period divided by the production quantity.
Each CSPS is manned by a single operator, which obtains arriving usables in accordance with the operation policy, Reserve-dependent and Sequential Range Policy (RdSRP) with control variable c (Matsui [3,6,15]). This shows a cycle of productive activity (called work-cycle time). The work-cycle time, Z, is a service time, X, plus a delay (or idle) time, D, involved in obtaining usables from the conveyor. Usables are units suitable for utilization by the CSPS, and the usables that arrive during the service time overflow along the conveyor.
Generally, the production, rate, r, is given by the reci-
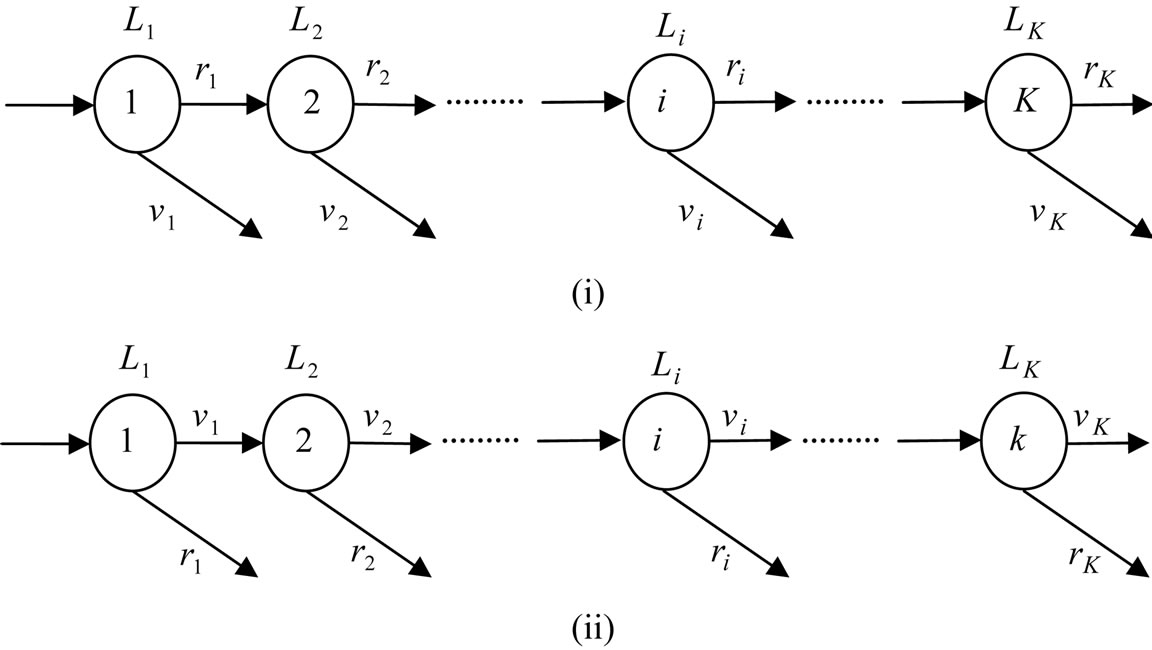
Figure 1. Two types of SCA. (i) Type I: Cyclic type (series system); (ii) Type II: Semi-cyclic type (ordered-entry system).
procal of cycle time, Z. Then, the production rates of Models I and II are respectively represented as follows:
 (2.3)
(2.3)
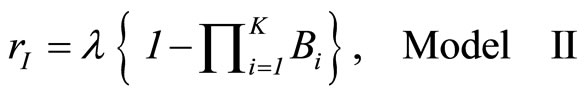 (2.4)
(2.4)
in which  and
and , are the probability of processing and loss, respectively.
, are the probability of processing and loss, respectively.
That is to say, the production rates for any network may be derived freely from the Equations (2.3) and (2.4). This production rate may be maximized at the balancing point, that is,  or
or . Also, there is the optimal cycle time (demand speed) for balancing.
. Also, there is the optimal cycle time (demand speed) for balancing.
3. Economic Balancing by SCA
3.1. Effect of Cost Decomposition
Now, we would propose a universal treatment for SCA. This is the transformation from physical (multiplicative) to economic (additive) domain, and would be superior to help the development of SCA at from the cyclic type to semi-cyclic type.
First, we consider this balancing point by the cost decomposition. In Feyzbakhsh et al. [16], the operating cost of CSPS is given by
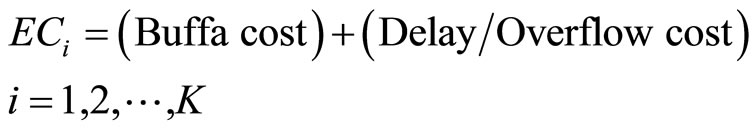 (3.1)
(3.1)
Then, the total cost of Models I or II is as follows:
 (3.2)
(3.2)
Tables 1 and 2 give a simulation comparison of station vs system-centered design, and show the validity and economy of station-centered approach. That is, the production rate would be changeable from the product form to the sum form, and the balancing point would be attainable at the even cost of each station.
3.2. Ellipse Hypothesis of Network
Next, we consider this balancing point at the network of Management Game Model (MGM) by Matsui [9,17]. Generally, the economic function of MGM is given by being similar to the cycle time as follows:
 (3.3)
(3.3)
in which the (operating) cost part is assumed to be similar to the traffic accounting as follows:
 (3.4)
(3.4)
where , is traffic intensity, and
, is traffic intensity, and ,
,  , are penalty costs.
, are penalty costs.

Table 1. Station vs system-centered design: d—viable case.

Table 2. A comparison of computational time: d = 0.9,  (Yamada and Matsui [11]).
(Yamada and Matsui [11]).
For reliability, the following lead time:
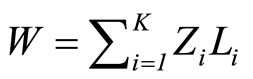 (3.5)
(3.5)
is introduced from Matsui’s equation, an extensive form of Little’s formula (Matsui [15,17]).
In there, the ellipse theory of enterprises was first found on a pair-matrix table in a Two-Center model (MGM), consisting of sales and production centers (Matsui [9]). The pair-matrix is formed by input (demand) variable in column and output (supply) in row. This theory is also the ellipse-cross theory of economics and reliability.
That of economics has two poles of revenue maximum and cost minimum, and the profit maximum is located in the medium zone. Also, that of reliability (busy time, BT) has two poles of lead time minimum and maximum. Following on, the two medium zones are the cross-region for the two ellipses.
Recently, the ellipse hypothesis of SCM was proposed in a series chain by Matsui & Motohashi [18]. Figure 2 shows the ellipse-cross theory of economics, EN, and reliability, BT, on the balance matrix, formed by the respective processing speeds of enterprises. The ellipsecross theory means that the maximal sum of profits is in

Figure 2. Ellipse hypothesis of SCM.
the middle on the balance matrix, and as follows, the profits and workloads are respectively even. This invisible balancing is a kind of integral optimization (Matsui & Ichihara [12]).
4. Semi-Cyclic Types
4.1. Manufacturing Type Model of SCM
For the study, we present two parallel models consisting of heterogeneous enterprises (agents). These situations are assumed under the different institutional environment of past research. One is the manufacturing type of makeor-buy, and the other is the sales type of supplier-retailers.
The first model consists of two communicated maketo-order enterprises under globalization. Suppose that Job-shop 1 is a domestic and high cost shop, EC1, while Job-shop 2 is in China and a low cost shop, EC2. Also, the profitable orders are accepted at Job-shop 1, and the rejected orders are accepted at Job-shop 2.
Thus, Job-shop 1 decides the make-or-buy action without comeback by a selection criterion (input speed), c, and may have the stock level of backlog, N. Job-shop 2 may have the stock level of backlog, M, and, if the number of backlog is over M, then an order arriving is lost.
Job-shop 2 is in communication with Job-shop 1, but both are in non-cooperative relation.
Figure 3 shows the ellipse shape on balancing table under even-cost ratio. This ellipse shape is a class of ellipse-cross theory of SCM. Note that the sum cost is not minimal but medium in balancing zone.
4.2. Sales Type Model of SCM
The second model is a multi-echelon-like system, and consists of a supplier and two order retailers. The supplier has an infinite capacity, but the two heterogeneous retailers have the stock level of N and M, respectively, in the VMI manner. Also, the supplier has a truck with capacity (travel time), and replenishes the goods (with price ) to the retailers at the approximate rate (input speed),
) to the retailers at the approximate rate (input speed), .
.
Figure 4 shows the ellipse shape on balancing table under relative-cost ratio. This ellipse shape is a class of ellipse-cross theory, but is in-complete in reliability.
5. Conclusions
In this paper, we reviewed a station-centered approach to Collaborative network, and presented the invisible collaboration in autonomous balancing at dual network of series and parallel types. Also, this result shows the importance role (invisible hand) of Ellipse hypothesis at the network collaboration/balancing of not only cyclic type but also semi-cyclic type.
In the near future, we would try to treat a structural framework for the economic analysis of interindustry relationship (EAIR) by this station-centered approach. This attempt would accompany with the MGM unit and traffic accounting (Matsui [9,10], Marukuni et al. [19]) at each body (station) in the demand and supply network.

Figure 3. Balancing table and ellipse of manufacturing type.
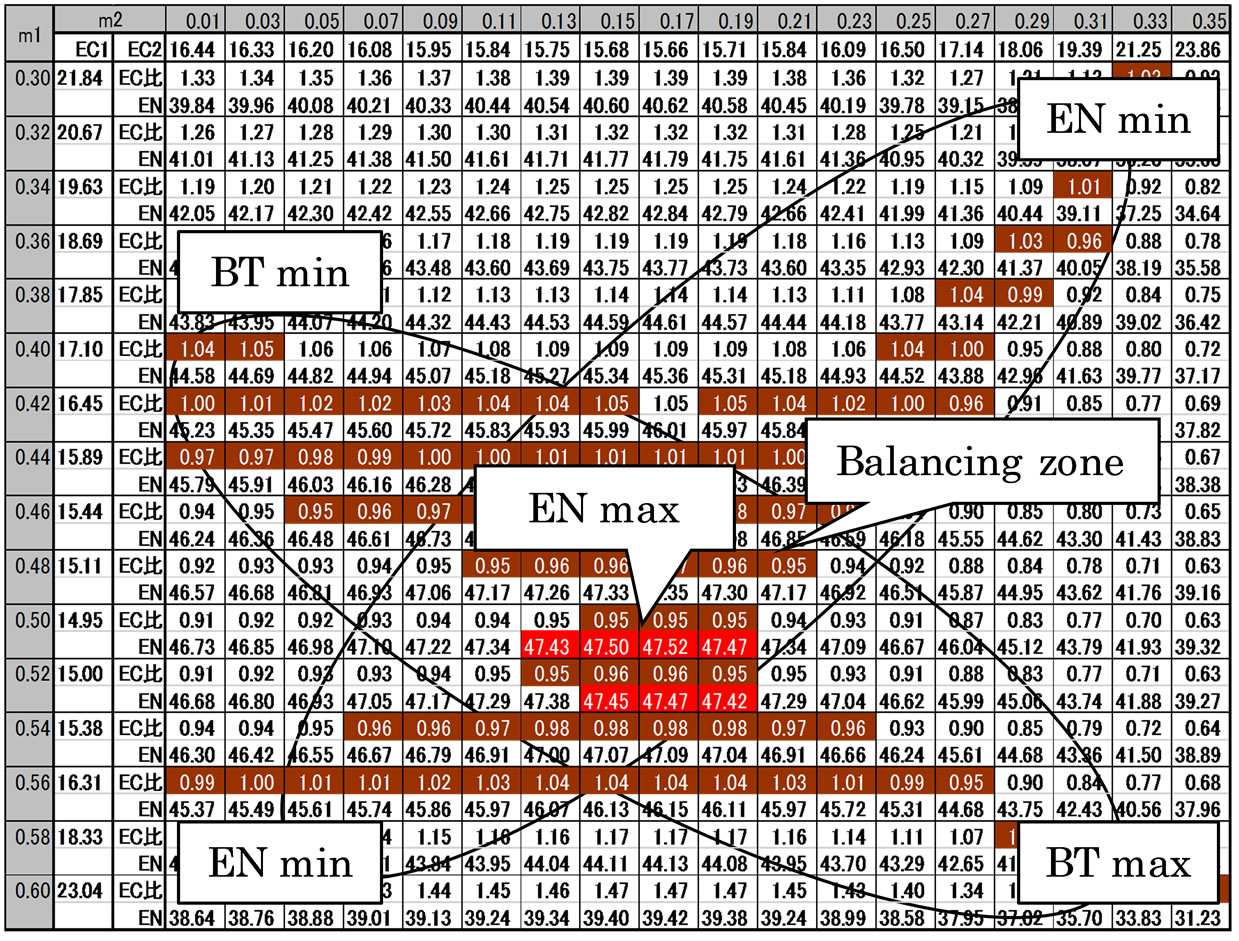
Figure 4. Balancing table and ellipse of sales type.
Finally, we would thank to M. H. Iizuka, my master student, for his help in a numerical example.
REFERENCES
- L. L. Reis, J. J. Brennan and R. M. Crisp Jr., “A Markovian Analysis for Delay at Conveyor-Serviced Production Station,” International Journal of Production Research, Vol. 5, No. 3, 1967, pp. 201-211. doi:10.1080/00207546708929752
- M. Matsui, T. Shingu and Makabe, “Conveyor-Serviced Production System: An Analytic Framework for StationCentered Approach by Some Queueing Formulas,” Preliminary Reports of the Operations Research Society of Japan, 1997, pp. 104-107.
- M. Matsui, “A Study on Optimal Operating Policies in Conveyor-Serviced Production System,” Doctoral Dissertation, Tokyo Institute of Technology, Tokyo, 1981.
- M. Matsui, “Conveyor-Like Network and Balancing,” In: A. B. Savarese, Ed., Manufacturing Engineering, NOVA Science Publishers, Inc., New York, 2011, pp. 65-87.
- G. C. Hunt, “Sequential Arrays of Waiting Lines,” Operations Research, Vol. 4, No. 6, 1956, pp. 674-683. doi:10.1287/opre.4.6.674
- M. Matsui, “Conveyor-Serviced Production System: Queueing Formulas, CSPS Analysis and 2-Level Mathematical Formulation,” Unpublished Paper, 1982.
- R. J. Aumann, “Subjectivity and Correlation in Randomized Strategies,” Journal of Mathematical Economics, Vol. 1, No. 1, 1974, pp. 69-96. doi:10.1016/0304-4068(74)90037-8
- M. Matsui, “An Optimal Design Problem of Production and Queueing Systems, Symposium on Performance Models for Information Communication Networks,” Optimal Economic Design of Production and Queueing Systems, Abstracts of APORS’94, Fukuoka, 1994, p. 266.
- M. Matsui, “A Management Game Model: Economic Traffic, Lead time and Pricing Setting,” Journal of Japan Industrial Management Association, Vol. 53, No. 1, 2002, pp. 1-9.
- M. Matsui, “Manufacturing and Service Enterprise with Risks: A Stochastic Management Approach,” Springer, New York, 2008.
- T. Yamada and M. Matsui, “2-Stage Design Method for Assembly Line System: A Unified Approach,” Journal of Japan Industrial Management Association, Vol. 51, No. 6, 2001, pp. 538-549.
- M. Matsui and S. Ichihara, “A Game Approach to SCM: Modeling, Formulation Example and Integral Optimization,” Journal of Japan Society of Logistics Systems, Vol. 4, No. 1, 2003, pp. 67-80.
- M. Matsui, “Economic (Re-)Balancing Problem: A Visualization of Invisible Hand and Ellipse Theory for MultiCenter,” Proceedings of International Conference on Production Research, Stuttgart, 31 July-3 August 2011, on CD-ROM.
- M. Matsui and Y. Dai, “Parallel SCM: Balancing Issues of Make-or-Buy and Supplier-Retailers Types,” Journal of Japan Industrial Management Association, Vol. 60, No. 1, 2009, pp. 1-10.
- M. Matsui, “CSPS Model: Look-Ahead Controls and Physics,” International Journal of Production Research, Vol. 43, No. 10, 2005, pp. 2001-2025. doi:10.1080/00207540412331331416
- S. A. Feyzbakhsh, M. Matsui and K. Itai, “Optimal Design of a Generalized Conveyor-Serviced Production Station: Fixed and Removal Item Cases,” International Journal of Production Economics, Vol. 55, No. 2, 1998, pp. 177-189. doi:10.1016/S0925-5273(98)00058-9
- M. Matsui, “Economic Demond-Balancing Problem of Multi-Center,” In: A. Tavidze, Ed., Economics, Trade and Globalization, Progress of Economics Research, NOVA Scientific Publishers, Inc., New York, Vol. 25, 2012, pp. 227-235.
- M. Matsui and M. Motohashi, “A Basic Study for Strategic Supply Chain Balancing,” Journal of Japan Society of Logistics Systems, Vol. 7, No. 1, 2007, pp. 21-31.
- S. Marukuni, M. Matsui and N. Ishii, “Introductory Traffic Accounting Practice for Advanced Management,” Proceedings of APIEMS 2010, Melaka, 7-10 December, 2010, on CD-ROM.

