Journal of Global Positioning Systems (2002)
Vol. 1, No. 1: 40-47
Accuracy Performance of Virtual Reference Station (VRS) Networks
Günther RETSCHER
Vienna University of Technology Department of Applied and Engineering Geodesy Gusshausstrasse 27-29 E128/3 A – 1040 Wien, AUSTRIA
Received: 24 February 2002 / Accepted: 30 May 2002
Abstract. Recent developments in differential GPS
(DGPS) services have concentrated mainly on the
reduction of the number of permanent reference stations
required to cover a certain area and the extension of the
possible ranges between reference and rover stations.
Starting from networked DGPS stations where all stations
are linked to a central control station for data correction
and modeling, the most advanced technique nowadays is
based on the virtual reference station (VRS) network
concept. In this case, observation data for a non-existing
“virtual” station are generated at the control center and
transmitted to the rover. This leads to a significant
improvement in positioning accuracy over longer
distances compared to conventional DGPS networks.
This paper summarizes the various DGPS architectures
and the corresponding accuracy. This is followed by a
description of the models and algorithms used for the
VRS station concept. Practical examples of correction
data services in Europe are given to highlight the
achievable positioning accuracy. The results of an
analysis of test data in a virtual reference station network
in southern Germany show that always a horizontal
positioning accuracy in the order of ± 5 cm can be
achieved for baselines with a length up to 35 km.
Key words: GPS, DGPS, VRS, RTK
1 DGPS NETWORK ARCHITECTURES
1.1 Single reference station concept
Figure 1 shows the architecture for the single reference
station concept. In this case, a reference station in a
DGPS network consists of the following main
components: a GPS antenna/receiver assembly; a wireless
data communication link to the user (usually a radio link);
the reference station software on a PC which performs
station monitoring, DGPS data correction model
estimation and data archiving; interfaces and
communication links for data transfer to the user
[Landau, 2000]. For integrity monitoring, a reference
station usually consists of 2 independent GPS receivers to
guarantee against system failure. The user receives either
DGPS corrections for code positioning or real-time
kinematic (RTK) GPS data for carrier phase positioning
in RTCM (Radio Technical Commission for Maritime
Services) format. As the observation errors and biases are
not modelled in the network, the error budget shows a
distance dependent growth as the user-to-station
separation increases [Retscher and Moser, 2001].
Fig. 1 Single reference station design
1.2 Multiple station concept
In the second concept, multiple reference stations are
connected to a central control station using a data
communication link (wireless radio link or cable
connection via local area network (LAN) or Internet).
Additional equipment at the reference station includes a
modem for data transfer and modification of the station
software package. The data transfer protocol employed
between each reference station and the control center is
usually RSIM (Reference Station Integrity Monitor
messages). Further information about the data format

Retscher: Accuracy Performance of VRS Networks 41
standards may be found in [Moser, 2001]. On the control
station, software is used to monitor several reference
stations simultaneously.
Fig. 2 Multiple reference station design with control center
1.3 Networked DGPS system concept
Due to the use of networked DGPS system concepts, a
reduction in initialization time for carrier phase
positioning (i.e., time required for resolving the carrier
phase ambiguities) and accuracy improvement for longer
ranges is achieved. Additionally the reliability of the
position solutions are improved allowing a larger
reference-to-user separation. Thereby the system
architecture is similar to the multiple reference station
concept (Figure 2), only due to the software modification
for data modeling in the control center a networked
solution is obtained. The software modification includes
new models for correction data estimation for modeling
of the major error sources, i.e., the satellite orbit errors,
ionospheric refraction as well as satellite and receiver
clock errors. For the modeling observation data from at
least three multiple reference stations are required. Then
so-called area correction parameters [Wanninger, 1999]
can be deduced for each triangle of three reference
stations in a network.
Other advantages of a networked DGPS station network
include the possibility for detecting station malfunction
or failure. Figure 3 compares the positioning accuracies
which are achieved over the SATVB reference station
network in Burgenland, Austria [Retscher and Chao,
2000] for a standard DGPS network on the left (Figure 3
(a)) and the networked solution on the right (Figure 3
(b)). From the comparison it can be seen that due to the
networked solution an accuracy of better than ± 2 cm can
be achieved for the whole area of Burgenland using only
4 reference stations where the station separation ranges
between 40 to 50 km. In the standard DGPS network the
position accuracy degrades as the user-to-station
separation increases and reaches values of ± 5 cm at a
distance of 50 km from the nearest reference station.
(a) Standard DGPS solution for four independent reference stations
(b) Networked DGPS solution with an additional central control
station
Fig. 3 SATVB network in Burgenland, Austria with 4 CORGS (Contiuous Operating Reference Geodetic Stations) [after Titz, 1999]

42 Journal of Global Positioning Systems
1.4 Virtual reference station network concept
Currently the most advanced approach for increased
spatial separation of permanent stations and error
modeling is the so-called virtual reference station (VRS)
network concept. The concept was firstly introduced in a
part of the German reference station network SAPOS
[Landau, 2000; Trimble, 2001]. The name of this
approach results from the fact that observations for a
“virtual” non-existing station are created from the real
observation of a multiple reference station network. This
allows to eliminate or reduce systematic errors in
reference station data resulting in an increase of distance
separation to the reference station for RTK positioning
while increasing the reliability of the system and reducing
the initialization time.
The system architecture is shown in Figure 4. To create
the virtual reference station data for a certain RTK GPS
rover station, the user receiver’s approximate location
accurate to about 100 m is transmitted to the network
control center. As a result, a bi-directional communication
link between the user and the control center is required.
The communication is usually performed using cellular
phones (Global System for Mobile Communication
GSM, in future Universal Mobile Telecommunication
Service UMTS). The observations for a given location are
estimated in the control center using real-time correction
models and then transferred in the RTCM format to the
rover station. On the rover side, standard RTK GPS
algorithms are employed to obtain the position fix.
Fig. 4 System architecture of the virtual reference station concept [after Trimble, 2001]
1.5 Virtual reference cell concept
Another possibility for networked DGPS solutions is the
virtual reference cell (VRC) concept. Here the correction
models are not estimated for a specific user on request as
in VRS concept, but the models are estimated for a given
gridded DGPS service area. The rover receiver is
assigned to a cell and there is no need for the virtual
station to follow the movement of the rover station. When
the rover leaves a VRC cell, then it is assigned to a new
cell. The main advantage using this concept is that there
is no limitation in the number of users and no bi-
directional communication link between the rover and the
control center is required. The positioning accuracy,
however, is lower than the accuracy which can be
achieved using the VRS approach. The VRC concept is
therefore mostly employed in WADGPS (Wide Area
DGPS) networks, such as the services provided by Thales
and Fugro. Further information about this services may

Retscher: Accuracy Performance of VRS Networks 43
be found in e.g. [Moser, 2001], [Retscher and Moser,
2001].
2 ERROR BUDGET AND MODELING
The main error sources and the models employed in
WADGPS networks have been discussed in detail in
[Retscher and Chao 2000]. The models can be adapted to
suit the requirements for correction data estimation in
networked DGPS services or in the virtual reference
station network concept. As usual, the main error sources
that have to be dealt with are the satellite orbit errors,
ionospheric refraction as well as satellite and receiver
clock errors. For the error budget see [Kaplan, 1996] and
for a detailed discussion of the error modeling see
[Ashkenazi et al., 1997; Retscher and Moser, 2001;
Whitehead et al., 1998]. In general, the approaches can be
classified into the following three types:
• Estimation of range corrections: In this case, networked
solutions are used to estimate the range corrections
from weighted observations of a multiple reference
station network. The main disadvantage is that the
positioning accuracy gets worse depending on the
distance between the user and the central point of the
multiple reference station triangle.
• Estimation of position corrections: Position dependent
algorithms estimate the position correction from the
weighted average of the rover positions derived from
each reference station. The accuracy degrades in a
similar way to the method using the range correction
approach.
• Estimation of corrections for the cell area: In the third
approach, the range error is divided into different
components that are estimated in a cell area
independently from the baselines between the reference
and rover stations. The user receives DGPS corrections
that are separated into several components and must
combine them to determine a position solution. The
calculation of the corrections is an iterative process.
This approach is most commonly applied and has many
advantages compared to the first two algorithms named
above. The disadvantage, however, is that the
corrections have to be applied at the rover and a
modification of standard DGPS algorithms would be
necessary. This problem has been solved using the
VRS approach.
For real-time applications, these error models have to be
predicted ahead. An approach for a dynamic orbit
determination has been introduced in [Retscher and Chao,
2000]. It can be summarized that then the satellite orbits
can be obtained with an accuracy of better than 10 m
r.m.s. using dual frequency raw pseudorange data from
only three reference stations. The accuracy is further
improved using data from more than three multiple
reference stations. In the dynamic orbit determination
algorithm also ionospheric correction parameters can be
estimated in an integrated Kalman filter approach.
Thereby the TEC (Total Electron Content) is estimated
using modified standard single layer models (e.g. a
modified Klobuchar model) [Klobuchar, 1986;
Kleusberg, 1998]. The clock errors are depending on the
other two error sources. They are estimated in an iterative
process and due to the improvement of the estimates of
the other error sources their impact is reduced. Site-
specific errors (e.g. multipath) can not be taken into
account as it has to be assumed that the reference stations
are situated at ideal locations and at the user site these
error sources are also minimized.
3 RESULTS OF TEST IN A VIRTUAL REFERENCE
STATION NETWORK
The performance and accuracy achievements of the
virtual reference station concept were analysed and
presented in [Retscher and Moser, 2001]. The main
results are summarized here. The VRS test network in
southern Germany of the company Trimble (Terrasat) is
shown in Figure 5. For the analysis presented here, the
observation data for three stations (Virtuell 1 to
Virtuell 3, see Figure 6) in the VRS network was
downloaded from the website of the company Terrasat1.
In total, 112 measurement epochs have been processed.
To analysis the distance dependance of the result, the
station Höhenkirchen was chosen as reference station in
all tests. In the first analysis, the accuracy of the solution
was investigated, followed by an analysis of system
performance and the overall precision of the result.
Fig. 5 VRS test network of the company Trimble (Terrasat) in Bayern,
Southern Germany (Map not to scale)
1 Website for Download of VRS observation data: www.virtualrtk.com

44 Journal of Global Positioning Systems
Fig. 6 Virtual reference station locations (Virtuell 1 to Virtuell 3)
3.1 Accuracy of the solution for the VRS stations
Table 1 shows the standard deviations of the processing
results for the VRS stations (Virtuell 1 to Virtuell 3). The
observations have been treated as kinematic observations
and positions were processed independently for each
measurement epoch. Figure 7 shows a classification of
the standard deviations of the horizontal coordinates
using a class interval of 10 cm. As expected, it can be
seen from Table 1 that the standard deviation increases
over larger distances from the reference station (i.e.,
station Höhenkirchen). On the other hand, surprisingly,
the standard deviations of station Virtuell 2 and Virtuell 3
have nearly the same value, although the station
Virtuell 3 is 18 km further away from the reference
station Höhenkirchen than Virtuell 2. The reason for this
phenomenon may be the fact that the station is located
outside the triangle of the three multiple reference
stations (see Figure 6) which are used to estimate the
correction parameters in VRS reference station network.
Tab. 1 Standard deviations of the kinematic solution for the VRS
stations Virtuell 1 to Virtuell 3
Standard deviations in [cm]
horizontal coord. Height
+/- 2.0 +/- 4.3
+/- 34.4 +/- 65.2
Point No.
Virtuell 1
Virtuell 2
Virtuell 3 +/- 37.1 +/- 68.8
Fig. 7 Standard deviations of horizontal coordinates of the virtual
reference stations (classification with intervals of 10 cm)
3.2 Overall precision of the result for the VRS stations
The overall precision of the result was obtained by
comparing the solution for the VRS stations with the true
values of the coordinates used to download the
observation data. Figure 8 shows a classification of the
deviations of the horizontal components X and Y for the
stations Virtuell 2 and Virtuell 3 where again a class
interval of 10 cm is used. As expected, the deviations for
station Virtuell 1 are very small and are not displayed in
Figure 8. The deviations follow a Gaussian distribution
which proves that no systematic errors occur in the data
sets.

Retscher: Accuracy Performance of VRS Networks 45
(a)
(b)
Fig. 8 Deviations of the horizontal component for the VRS stations Virtuell 2 (a) and Virtuell 3 (b) (classification with intervals of 10 cm)
The following major results can be summarized:
• The baseline accuracy of RTK GPS measurements is
usually described by a constant and a distance
dependent error, e.g. 5-20 mm ± 1-2 ppm. For a
baseline with a length of 10 km we would therefore get
an error of ± 40 mm in the worst case. In the analysed
concept of the VRS network, the maximum baseline
length is always very short as observations of a non-
existing “virtual” reference station are sent to the rover
station which is located nearby the rover. The baseline
length is given by the square root of the square sum of
the coordinate differences between the VRS and the
rover station. In our investigation the maximum
distance encountered was less than 1.05 m. Therefore
the precision of the position solutions for the rover
stations can be equated with the precision of the
corresponding VRS station. The precision of the VRS
station is given by the standard deviation of their
differences to the true values.
• For a comparison of all results the standard deviations
of the differences to the true values of the VRS stations
are summarized in Table 2. To achieve comparable
values at a probability level of 99%, the standard
deviations of the measurements of 112 epochs have to
be multiplied by a quantile of 1.211 which is obtained
from a student probability distribution. The results
show reasonable values for the standard deviations of
the X and Y coordinates for distances up to 30 km from
the network center point. In addition, the standard
deviations are also compared to values published by the
company Trimble (Terrasat) for the station Neufahrn.
They have been obtained from a continuous RTK
observation over a period of several hours. As can be
seen from Table 2 similar results are obtained for the
horizontal component, the standard deviations of the

46 Journal of Global Positioning Systems
height component, however, are much smaller. The
reason for this may be the fact that a larger number of
RTK results are available which are used to calculate
the standard deviation as the length of the observation
period was about 90 hours.
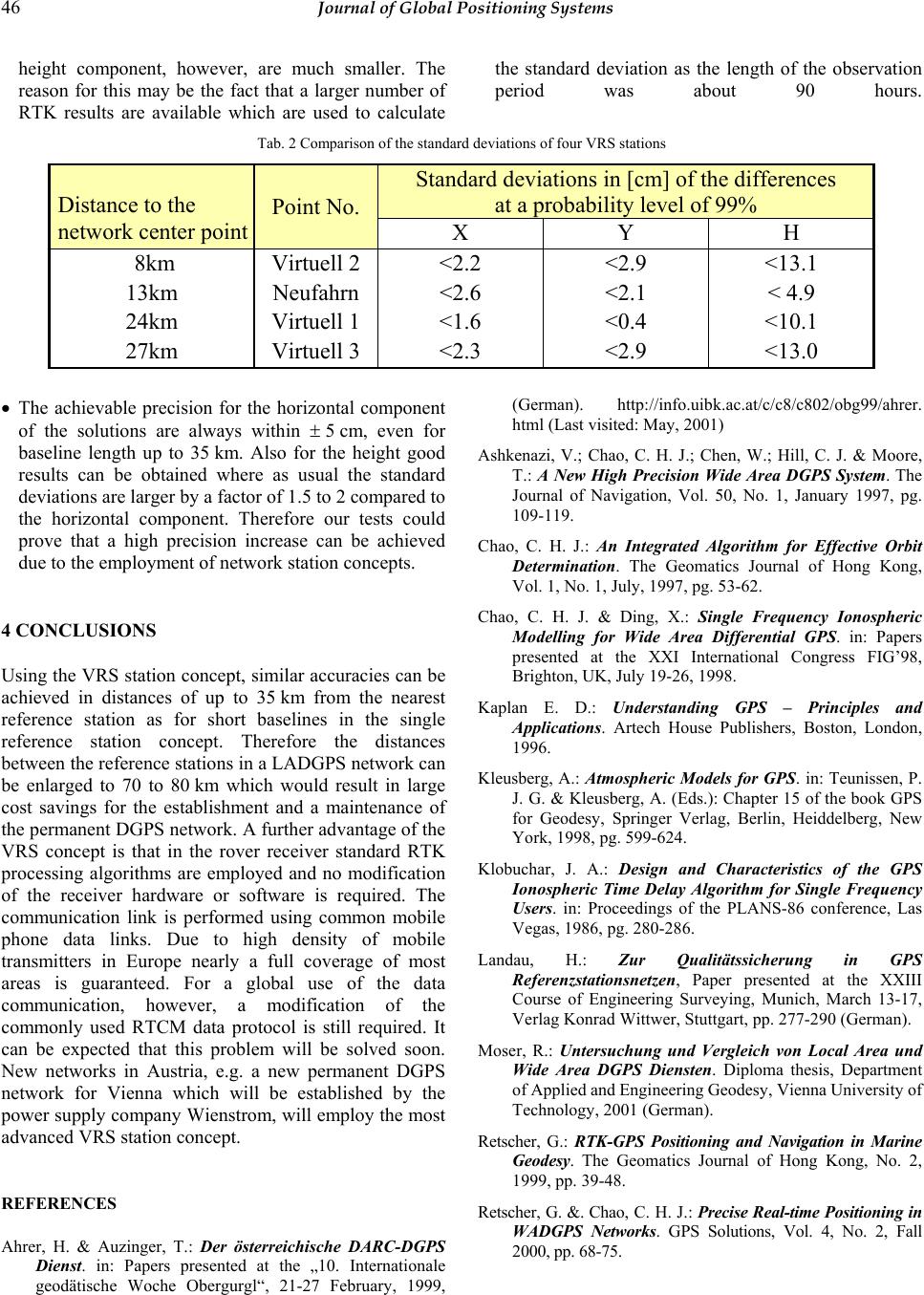
Tab. 2 Comparison of the standard deviations of four VRS stations
Standard deviations in [cm] of the differences
at a probability level of 99% Distance to the
network center point
Point No.
X Y H
8km Virtuell 2 <2.2 <2.9 <13.1
13km Neufahrn <2.6 <2.1 < 4.9
24km Virtuell 1 <1.6 <0.4 <10.1
27km Virtuell 3 <2.3 <2.9 <13.0
• The achievable precision for the horizontal component
of the solutions are always within ± 5 cm, even for
baseline length up to 35 km. Also for the height good
results can be obtained where as usual the standard
deviations are larger by a factor of 1.5 to 2 compared to
the horizontal component. Therefore our tests could
prove that a high precision increase can be achieved
due to the employment of network station concepts.
4 CONCLUSIONS
Using the VRS station concept, similar accuracies can be
achieved in distances of up to 35 km from the nearest
reference station as for short baselines in the single
reference station concept. Therefore the distances
between the reference stations in a LADGPS network can
be enlarged to 70 to 80 km which would result in large
cost savings for the establishment and a maintenance of
the permanent DGPS network. A further advantage of the
VRS concept is that in the rover receiver standard RTK
processing algorithms are employed and no modification
of the receiver hardware or software is required. The
communication link is performed using common mobile
phone data links. Due to high density of mobile
transmitters in Europe nearly a full coverage of most
areas is guaranteed. For a global use of the data
communication, however, a modification of the
commonly used RTCM data protocol is still required. It
can be expected that this problem will be solved soon.
New networks in Austria, e.g. a new permanent DGPS
network for Vienna which will be established by the
power supply company Wienstrom, will employ the most
advanced VRS station concept.
REFERENCES
Ahrer, H. & Auzinger, T.: Der österreichische DARC-DGPS
Dienst. in: Papers presented at the „10. Internationale
geodätische Woche Obergurgl“, 21-27 February, 1999,
(German). http://info.uibk.ac.at/c/c8/c802/obg99/ahrer.
html (Last visited: May, 2001)
Ashkenazi, V.; Chao, C. H. J.; Chen, W.; Hill, C. J. & Moore,
T.: A New High Precision Wide Area DGPS System. The
Journal of Navigation, Vol. 50, No. 1, January 1997, pg.
109-119.
Chao, C. H. J.: An Integrated Algorithm for Effective Orbit
Determination. The Geomatics Journal of Hong Kong,
Vol. 1, No. 1, July, 1997, pg. 53-62.
Chao, C. H. J. & Ding, X.: Single Frequency Ionospheric
Modelling for Wide Area Differential GPS. in: Papers
presented at the XXI International Congress FIG’98,
Brighton, UK, July 19-26, 1998.
Kaplan E. D.: Understanding GPS – Principles and
Applications. Artech House Publishers, Boston, London,
1996.
Kleusberg, A.: Atmospheric Models for GPS. in: Teunissen, P.
J. G. & Kleusberg, A. (Eds.): Chapter 15 of the book GPS
for Geodesy, Springer Verlag, Berlin, Heiddelberg, New
York, 1998, pg. 599-624.
Klobuchar, J. A.: Design and Characteristics of the GPS
Ionospheric Time Delay Algorithm for Single Frequency
Users. in: Proceedings of the PLANS-86 conference, Las
Vegas, 1986, pg. 280-286.
Landau, H.: Zur Qualitätssicherung in GPS
Referenzstationsnetzen, Paper presented at the XXIII
Course of Engineering Surveying, Munich, March 13-17,
Verlag Konrad Wittwer, Stuttgart, pp. 277-290 (German).
Moser, R.: Untersuchung und Vergleich von Local Area und
Wide Area DGPS Diensten. Diploma thesis, Department
of Applied and Engineering Geodesy, Vienna University of
Technology, 2001 (German).
Retscher, G.: RTK-GPS Positioning and Navigation in Marine
Geodesy. The Geomatics Journal of Hong Kong, No. 2,
1999, pp. 39-48.
Retscher, G. &. Chao, C. H. J.: Precise Real-time Positioning in
WADGPS Networks. GPS Solutions, Vol. 4, No. 2, Fall
2000, pp. 68-75.

Retscher: Accuracy Performance of VRS Networks 47
Retscher, G. & Moser, R.: Untersuchung und Vergleich von
Local Area und Wide Area DGPS Diensten. Allgemeine
Vermessungsnachrichten, No. 10, October 2001 (German).
Teunissen, P. J. G.: GPS Carrier Phase Ambiguity Fixing
Concepts. in: Teunissen, P. J. G. & Kleusberg, A. (Eds.):
Chapter 15 of the book GPS for Geodesy, Springer Verlag,
Berlin, Heiddelberg, New York, 1998, pg. 319-388.
Titz, H. & Weber, R.: SATVB – A multipurpose
GPS/GLONASS reference station network in
Burgenland/Austria. in: Papers presented at the
Symposium on Geodesy for Geotechnical and Structural
Engineering, April 20-22, 1998, Eisenstadt, Austria, pg.
564-569.
Trimble (Terrasat): Introducing the Concept of Virtual
Reference Stations into Real-Time Positioning. Technical
information, 2001. http://www.terrasat.com/applications/
refvirtual.htm (Last visited: January, 2002)
Whitehead, M. L.; Penno, G.; Feller, W. J.; Messinger, I. C.;
Bertiger, W. I.; Muellerschoen, R. J.; Iijima, B.A. &
Piesinger, G.: Satloc Real-Time Wide Area Differential
GPS System. GPS Solutions, Volume 2, Number 2, 1998,
pp. 46-63.