Journal of Electromagnetic Analysis and Applications
Vol.06 No.11(2014), Article ID:50215,15 pages
10.4236/jemaa.2014.611035
Transient Behavior of a System Composed of Conductive Thin Wire Structures Excited by Harmonic and Lightning Type Signals
Eduardo Faleiro1, Gabriel Asensio2, Daniel García3, Gregorio Denche3, Jorge Moreno3
1Departamento de Física Aplicada, ETSIDI, Universidad Politécnica de Madrid, Madrid, Spain
2Departamento de Matemática Aplicada, ETSIDI, Universidad Politécnica de Madrid, Madrid, Spain
3Departamento de Ingeniería Eléctrica, ETSIDI, Universidad Politécnica de Madrid, Madrid, Spain
Email: eduardo.faleiro@upm.es, gabriel.asensio@upm.es, daniel.gpuertas@upm.es, gdenche@ree.es,
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2014; revised 13 August 2014; accepted 11 September 2014
ABSTRACT
The transient response of a system of independent electrodes buried in a semi-infinite conducting medium is studied. Using a simple and versatile numerical scheme written by the authors and based on the Electric Field Integral Equation (EFIE), the effect caused by harmonic signals ranging on frequency from Hz to hundred of MHz, and also by lightning type driving signal striking at a remote point far from the conductors, is extensively studied. The value of the scalar potential appearing on the electrodes as a function of the frequency of the applied signal is one of the variables investigated. Other features such as the input impedance at the injection point of the signal and the Ground Potential Rise (GPR) over the electrode system are also discussed.
Keywords:
Transferred Potentials, Thin Wire Structures, Lightning Pulses, Electric Field Integral Equation, Method of Moments

1. Introduction
When a metallic conductor (the active electrode) is buried in a semi-infinite medium of non-zero conductivity, and is energized by either a voltage or a current signal variable in time, an electromagnetic field, which is produced by the induced currents, is established within the electrode and into the surrounding medium which produces an elevation of the electrical potential in all the space and in particular on the ground surface or GPR, [1] -[4] .
When metallic electrodes are located in the vicinity of the active electrode, even if they are not energized (passive electrodes), induced currents appear as a result of the interaction between them, all of which now form a system of interacting conductors and their potential will differ from the one they have when they are isolated or not part of the system [5] [6] . In this case we speak of transferred potentials by active to passive electrodes. This is particularly important since a metallic mass in low frequency regime can be considered equipotential, which means that a conductor can transmit the effect of belonging to a system of conductors to large distances compared with the characteristic size of the system. Suffice it to consider such a linear passive electrode of great length that is near a small casual energized electrode and to transfer a non-zero potential. This potential may appear in certain circumstances throughout the linear electrode at great distance from where the energization occurrs.
Everyday events that fit this simplified description happen when a fault current occurs in a grounding electrode of an electrical installation which is close to other grounding electrodes of other facilities that are initially isolated [7] . The release of the ground fault current and the subsequent appearance of an electromagnetic field lead to an electromagnetic coupling occurring between all adjacent metallic electrodes and the appearance of a transferred potential on each passive electrode [8] .
In the present paper, based on the classic EFIE scheme proposed in [9] , the authors have developed a simple and very versatile numerical code that is capable of handling complex systems with multiple electrodes and multiple feeding points for arbitrary time signals. Although there is commercial software that could run part of the calculations given in this paper, the authors have preferred to start from its own calculation scheme adapted to the problem under study.
The numerical code used is based upon the Moment Method as studied by Harrington [10] , and can be applied to any electrode configuration composed of thin wires with any number of signal injection points working simultaneously [11] . Thus, it is possible to study the effect on the ground caused by the excitation of two buried electrodes of any shape and interconnected by an external conducting wire or, as in this work, the potential induced in the isolated passive electrodes of the system while only one of them is activated [12] -[14] .
In this paper we consider a system of two electrodes, a simple square grid buried in the ground, the active electrode, and a square loop conductor placed on the ground surface above the first electrode and electrically isolated from the first one, the passive electrode. We will study the behavior of the potential transferred to the passive electrode as a function of the frequency of the signal applied.
The grounding impedance for the active electrode as a function of the excitation frequency is also studied, because it is considered as one of the most important parameters in the design of grounding systems. Finally we study the effect that causes an intense and short excitation lightning type signal applied directly to the active electrode and also at a remote point on the ground far from the electrode system [15] [16] . This is intended to simulate the effect of a lightning strike on the vicinity of a facility grounding system consisting of a buried wire mesh and a metallic fence on the surface surrounding the installation.
2. Theoretical Foundations
When a perfect conductor is buried in a semi-infinite medium of conductivity σ and ε and μ electromagnetic parameters and is subjected to an harmonic excitation of frequency , the induced charges and currents act as sources of scalar
, the induced charges and currents act as sources of scalar 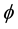 and magnetic
and magnetic 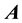 potentials, so that the electric field induced by the harmonic signal and created by the structure is (Figure 1).
potentials, so that the electric field induced by the harmonic signal and created by the structure is (Figure 1).
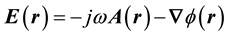 (1)
(1)
Scalar and vector potentials for the case of filamentary conductors have an expression with significant simplifications. In fact, taking the arc length 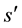 along the axis of the conductors as the independent variable.
along the axis of the conductors as the independent variable.
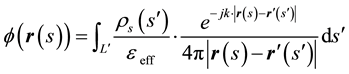 (2)
(2)
Figure 1. Curved thin wire conductor showing some of the variables used in the text.
 (3)
(3)
where everything is calculated along the axis of the wire, with the sole knowledge of the intensities 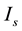 , along the conductor axis.
, along the conductor axis.
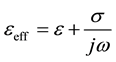 (4)
(4)
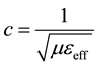 (5)
(5)
The calculation of currents is done by imposing the continuity of the tangential component of the total electric field, which is the sum of the exciting electric field and the induced electric field on the conductor surface. If the conductor is a PEC, the total electric field will be zero inside the conductor according to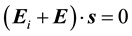 ,
, 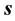 being a unit vector tangent to the conductor surface.
being a unit vector tangent to the conductor surface.
From the expression on the continuity of the tangential component of the total field, it follows that
 (6)
(6)
where the transient kernel has been introduced
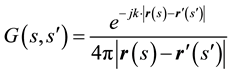 (7)
(7)
and the approximation has been used,
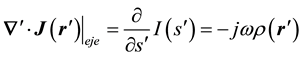 (8)
(8)
In order to work exclusively with the longitudinal currents

The second term of the RHS can be calculated by introducing the expression

which is a function of the variable


Considering these details,

but it is easy to check that 

which, in even more compacted, results

The Expression (13) is an integral equation for the variable

3. Numerical Solution and Application to Complex Systems
With the aim to find the distribution of longitudinal currents 
The Method of Moments is a numerical procedure that allows obtaining a solution to Equation (13) by reducing the integral equation to a matrix equation as defined by Harrington [10] . To do this, the overall curved wire of length




as an example, the unit step function can be chosen for

Note that this is a staircase-like approximation to the function




The choice of these functions 
Introducing the (14) into (13) and taking into account the definition of the basis functions it follows that,

expression valid at any point 


where, the points 


This gives us a system of 



The use of Dirac delta functions is not unique. If functions 


This procedure is known as Galerkin method and its main advantage is to ensure the electrode to be equipotential unlike the point matching method, in which only it is ensured that the electrode is equipotential at 
For the Galerkin method, the above expression is,

By application of the point matching method, considering the kernel 

where we have introduced the notation


in which we have established the following criteria: the segments are oriented from left to right assigning the left end to 






If we define the mutual impedance matrix as

and remembering that

Since 


which is a linear system of 


whose contribution to (27) is

which is valid for all




There only remains to be added the boundary condition associated with semi-infinite nature of the surroundings. For a perfectly horizontal surface that separates the conductive soil from the air, just consider the existence of a virtual electrode located symmetrically with respect to the horizontal ground surface and in an identical electrical state as the actual electrode. Currents must flow in such a way that they should be a mirror reflection of the actual ones with respect to the horizontal ground.
Under these conditions, the potential can be calculated correctly in any point at the ground. This does not apply to air, where the virtual electrode is located.
We introduce the mutual impedances by,

where F is a correction factor that takes into account the electrical parameters of the two media . For a rank of 


since the electrical conductivity of air is nearly zero,
In the above formula, 


In order to build the matrix of the complete system, including free ends and injection points, we extend the initial matrix size 



Finally, we propose a matrix impedances that is organized as

where the column vector of the RHS are known data corresponding to incoming-outgoing currents at the free ends


If the structure has no free ends being a loop, the impedances 
Once determined the distributions of charges and currents in the buried electrode, the relevant magnitudes and the electrical parameters can be calculated at any point in the ground. One of the most common ones is the absolute potential with respect to far earth at any point on the surface of the soil,

Using the entire set of operations made before, as the integration by parts, the method of moments for the numerical approximation, the introduction of the feeding points and discontinuity of the ground surface, a final expression is obtained,

where the following abbreviation it is introduced


4. Induced Potentials in the Electrode System
We will apply the above theoretical framework to the study of a system consisting of two conductors as shown in Figure 2. The lower regular mesh conductor, which will be called active conductor, which can be energized through the injection points IP1 and IP2 marked in Figure 2. The upper conductor, denominated as the passive conductor, is placed symmetrically on the active conductor and at the ground surface. Both conductors represent a simplified model of grounding protection facilities. In this model, the passive conductor simulates a metal fencing surrounding the facility.
First, the active conductor is energized by a defined frequency harmonic signal. With the help of the above theoretical expressions, the potential acquired by both electrodes will be calculated as a function of the frequency of the signal injected on the active electrode.
We are mainly interested in calculating the potential of the passive electrode, which simulates a metal fence surrounding an area electrically protected by the buried grid.
Potentials along point p2 to p4 of the buried grid and along the contour OABC on the passive electrode will be calculated at several frequencies.
The representative value of the potential will be its peak value, associated with the harmonic behavior of the electrode response.
The grounding impedance, as a function of the frequency, will be also calculated at the two feeding points IP1 and IP2.
Next, a fast and peaked pulse of electrical current is injected into the buried grid through the feeding point IP2 and the potential as a function of time is estimated on the points p3 and p4 of the active electrode. The same is done at the point p5 on the passive electrode. Finally, another fast and peaked pulse is injected into the ground surface far from the system of conductors at the external injection point EIP of Figure 2. The potential at points p1 to p5 is evaluated as a function of time. For both pulses, the potential appearing at the ground surface along the diagonal OB on the passive electrode is also evaluated.
The calculations were carried out for a 4 m length L of the upper conductor and 1 m length l for the wires on the bottom grid. The burial depth h is 0.5 m and the distance between the injection point EIP and the surface conductors D as seen in Figure 2, ranks from 2 m to 8m.
In all calculations, the electrodes are initially divided into 
Figure 2. System of electrodes, all buried at a depth h in a conducting soil. The system is composed of a regular mesh half-edged l, and of a square conductor on the surface edged L, which simulate a metallic fence.

with the values for the constants are 




4.1. Harmonic Regime
The active electrode is fed with a 10 A sinusoidal current and variable frequency injected through IP1 or IP2.
4.1.1. Grounding Impedance as a Function of Frequency for the Both Feeding Points IP1 and IP2
Defining the input impedance with respect to a feeding point, at a given value of the frequency

where 

Figure 3 shows the results for the modulus of the grounding impedance at injection points IP1 and IP2 as a function of the frequency of the harmonic signal injected.
It should be mentioned that at low frequency, the impedance values should be independent of the injection point with significant differences at medium and high frequency. Figure 3 shows that at low frequencies, there is a small difference in impedance values approximately 10%. This is explained by the segmentation of the electrodes considered here. Table 1 shows the values of the input impedance for IP1 and IP2 points at a frequency
Figure 3. Absolute value of the input grounding impedance associated to injection points IP1 (blue line) and IP2 (red line), as a function of the frequency decimal logarithm.
Table 1. Input impedance (module) to the injection points IP1 and IP2 at the frequency of 50 Hz, for several values of the partition into N segments of the rods.
of 50 Hz when the segmentation is refined.
It is clear that there is a convergence towards a common value of the grounding impedance and that the differences are due to the errors arising from the numerical treatment of the problem.
4.1.2. Harmonic Potential Values along p2 and p4 of Figure2 on the Active Electrode, When Considered IP2 as the Feeding Point
Figure 4 shows the potential phasors along the active electrode between points p2 and p4, in Figure 2 for low and medium frequency. It is noted that at low and medium frequency the potential profiles are very similar to each other. Significant differences are found from the frequency of 1 MHz on, at which the grounding impedance begins to grow significantly.
For high frequencies, as shown in Figure 5, the profiles are similar to each other but differ from those found
Figure 4. Potential profile along the points p2 to p4 (Figure 2) on the active electrode at the written frequencies.
Figure 5. The same as in Figure 4 but at higher frequencies.
at low frequencies. It is observed, that the voltage increases in the range between 1 and 10 MHz and has a certain saturation with oscillations in the vicinity of 450 volts, which corresponds with ripples observed in Figure 3 in the mentioned frequency range.
4.1.3. Peak Values of the Harmonic Potential in the Passive Electrode Contour OABC for IP2 as the Feeding Point
With respect to the passive electrode, for low and medium frequency, Figure 6 shows the potential profile along the electrode contour OABC. It is noteworthy that for low and medium frequency the induced potential in the passive electrode accounts for is between 31% and 37% of the potential recorded at the feeding point.
For high frequency, Figure 7 shows the induced potential in the passive electrode. As can be seen, it is substantially lower than those recorded at low and medium frequency. In this case induced potentials account for 4% of the potential in the feeding point.
Figure 6. Potential profile along the contour OABC on the passive electrode at the frequencies shown.
Figure 7. The same as in Figure 6, but at higher frequencies.
4.2. Impulse Response
We will study two completely different situations. On one hand a peaked and short in time signal starting immediately at 

4.2.1. Instantaneous Potential at Points p3 and p4 of the Active Electrode and at Point p5 on the Passive Electrode
When a lightning type 1 signal starting immediately at 
It can be seen that the peak of the induced potential on the passive electrode represents approximately 37% of the peak of the potential on the active electrode which is excited by the signal. The ripples that appear in the figures are due to the finite number of Fourier components of the driving signal with which we have worked.
4.2.2. Instantaneous Potential at Points p1 to p5 of Both Electrodes, When a Lightning Type 2 Signal Is Injected Far from the System of Conductors at EIP (See Figure 2)
Figure 9 shows the instantaneous potential appearing at the points p1 to p5 on the electrodes of the system,
Figure 8. Instantaneous potential at points p3 and p4 on the active electrode and at point p5 on the passive electrode when a lightning type 1 signal is injected at IP2.
Figure 9. Instantaneous potential at points p1 to p5 on the system (Figure 2) when a lightning type 2 signal is injected at EIP at D = 2 m.
when the distance between the EIP point and point p1 on the passive electrode is 2 m. In the subfigure, the instantaneous ground potential generated by the applied signal at the injection point EIP is represented.
When the distance 


Taking the potential peak at p1 as a function of the distance 

The coefficients with 95% confidence bounds have the values




4.2.3. Ground Potential Profile along the Diagonal OB (Figure 2), When a Lightning Type 1 Signal Is Injected at IP2
In Figure 12, the ground potential profile along the diagonal OB for several time values is represented. The sequence of graphs cover the period of time, in which the potential increases from the initial value and reaches its maximum value, decreasing thereafter. The two symmetrical peaks in the figure correspond to the passive elec-
Figure 10. Instantaneous potential at points p1 to p5 (Figure 2) for D ranging from 4 to 10 m from top to bottom and from the left to the right of the panel.
Figure 11. Potential at point p1 as a function of the distance D (Figure 2). The fitting to a power law, whose coefficients are in the text, is shown as a continuous red line superimposed.
Figure 12. Ground potential profile along the diagonal OB of Figure 2. A lightning type 1 signal strikes at IP2 and a time sequence is shown from t = 0 (line at the bottom) to the time when the ground potential reaches its maximum value.
trode potential at the points O and B because it is located on the ground.
4.2.4. Ground Potential Profile along the Diagonal OB (Figure 2), When a Lightning Type 2 Signal Is Injected at EIP
In Figure 13, the ground potential profile along the diagonal OB for several time values is also represented. As before, the sequence of graphs covers the period of time, in which the potential increases from the initial value and reaches its maximum value decreasing thereafter.
5. Conclusions
With the help of a numerical code written entirely by the authors and intended to solve the Electric Field Integral Equation (EFIE) for a thin wire structure, in this paper, we have studied the response of a system of independent electrodes to various types of driving signals. These signals are of two kinds, namely current harmonic signals injected directly on one of the electrodes, the active electrode, and lightning type signals injected at a point on the ground surface far away from the system, although they have also been directly applied to the active electrode.
Figure 13. Ground potential profile along the diagonal OB of Figure 2. A lightning type 2 signal strikes at EIP with D = 2 m far from p1. As in Figure 12, a time sequence is shown from t = 0 (line at the bottom) to the time when the ground potential reaches its maximum value.
The response has been measured by the scalar potential generated in the electrodes of both the system and the ground surface above the buried electrodes. In particular, it has been of great interest to determine the induced potential on the electrodes not directly excited in all cases studied.
It can be stated that, regardless of the size of the electrodes of the system and their relative positions, induced potentials appearing in the electrodes may represent a significant fraction of the potential generated by the drive signal, which can pose risks for equipment and staff.
It was also concluded from the preceding analysis, that the low frequency excitations induce a greater fraction of the driving potential in the passive electrode; however, at higher frequencies the vicinity of the injection point experiences a large potential rise while it decays significantly in the passive electrode.
Acknowledgements
The authors would like to thank the Departments of Electrical Engineering, Applied Mathematics and Applied Physics of the Escuela Técnica Superior de Ingeniería y Diseño Industrial (ETSIDI) at Polytechnic University of Madrid (UPM) for their support to the undertaking of the research summarized here. Furthermore, the authors appreciate the useful suggestions and selfless assistance of Prof. P. Navarro. Finally, the authors would like to thank Ms. Gabriela Andres for her contribution to the linguistic correction of the original paper.
References
- Grcev, L. and Dawalibi, F. (1990) An Electromagnetic Model for Transients in Grounding Systems. IEEE Transactions on Power Delivery, 5, 1773-1781. http://dx.doi.org/10.1109/61.103673
- Grcev, L. (1996) Computer Analysis of Transient Voltages in Large Grounding Systems. IEEE Transactions on Power Delivery, 11, 815-823. http://dx.doi.org/10.1109/61.489339
- Grcev, L. (1992) Computation of Transient Voltages Near Complex Grounding Systems Caused by Lightning Currents. Symposium Record of the IEEE 1992 International Symposium on Electromagnetic Compatibility, 92CH3169-0, 393- 400.
- Vuckovic, D.D. et al. (2012) Study on a Standard for Grounding Systems Realization. Serbian Journal of Electrical Engineering, 9, 393-401. http://dx.doi.org/10.2298/SJEE1203393V
- Colominas, I., et al. (2012) Advanced Computer Methods for Grounding Analysis. Proceedings of the World Congress on Engineering and Computer Science 2012 (WCECS 2012), Vol. II, San Francisco, 24-26 October 2012.
- Cristina, S. and Orlandi, A. (1992) Calculation of the Induced Effects Due to a Lightning Stroke. Proc. Inst. Elect. Eng. B, 139, 374-380.
- Charlton, T., Davies, M. and Baudin, D. (2007) Tranfer Potentials from MV to LV Installations during an Earth Fault. CIRED, 19th International Conference on Electricity Distribution, Vienna, 21-24 May 2007, Paper No. 0805.
- Poljak, D., et al. (2011) Electromagnetic Field Coupling to Multiple Buried Thin Wires. Proceedings of the 10th Symposium on Electromagnetic Compatibility, (EMC, Europe 2011), York, 26-30 September 2011, 272-277.
- Ala, G. and Di Silvestre, M.L. (2002) A Simulation Model for Electromagnetic Transients in Lightning Protection Systems. IEEE Transactions on Electromagnetic Compatibility, 44, 539-554. http://dx.doi.org/10.1109/TEMC.2002.804773
- Harrington, R.F. (1993) Field Computation by Moment Methods. IEEE Press, New York. http://dx.doi.org/10.1109/9780470544631
- Gibson, W.C. (2008) The Method of Moments in Electromagnetics. Chapman & Hall/CRC, Boca Raton.
- Wang, J.H. (1991) Generalized Moment Methods in Electromagnetics. Wiley Interscience, New York.
- Berberovic, S., Haznadar, Z. and Stih, Z. (2003) Method of Moments in Analysis of Grounding Systems. Engineering Analysis with Boundary Elements, 27, 351-360. http://dx.doi.org/10.1016/S0955-7997(02)00123-6
- Ala, G., Buccheri, P., Francomano, E. and Tortorici, A. (1994) An Advanced Algorithm for Transient Analysis of Grounding Systems by Moments Method. 2nd International Conference on Computation in Electromagnetics, London, 12-14 April 1994, 363-366.
- Liu, Y., Theethayi, N. and Thottappillil, R. (2005) An Engineering Model for Transient Analysis of Grounding System under Lightning Strikes: Nonuniform Transmission-Line Approach. IEEE Transactions on Power Delivery, 20, 722- 730. http://dx.doi.org/10.1109/TPWRD.2004.843437
- Geri, A. (1999) Behavior of Grounding Systems Excited by High Impulse Currents: The Model and Its Validation. IEEE Transactions on Power Delivery, 14, 1008-1017. http://dx.doi.org/10.1109/61.772347


















