Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 3 (2010) , Article ID: 1538 , 5 pages DOI:10.4236/jemaa.2010.23019
The Additional Criterion for the Determination of the Time of Minimum of a Solar Cycle
![]()
Pulkovo Observatory, St. Petersburg, Russia.
Email: abduss@gao.spb.ru
Received September 22nd, 2009; revised October 18th, 2009; accepted October 23rd, 2009.
Keywords: Sun, Solar Cycle, Solar Cycle Minimum, TSI, Sunspot Activity
ABSTRACT
The sunspot number is becoming an increasingly insufficiently reliable parameter for the determination of the time of minimum of a solar cycle during the prolonged and deep minimum of the 23rd solar cycle. Moreover, the sunspot number does not quantitatively reflect physical processes and is a practically conventional qualitative “noisy” parameter. Introduction of an additional criterion for the determination of the time of minimum of a solar cycle is becoming particularly topical due to the upcoming common descent of the level of the 2-secular cycle, when the amplitude of sunspot activity variation will sequentially decrease during several subsequent cycles (after the 23rd cycle). We propose the adoption of the smoothed minimal level of the total solar irradiance (TSI) as an additional physically justified criterion for the determination of the time of minimum of a solar cycle during the minimum of sunspot activity. The minimal level of the monthly average values of the TSI smoothed for 13 months when the last two of its values exceed the preceding value at the point of minimum will additionally indicate the time of minimum of a cycle. The additional criterion has been successfully used for the determination of the time of minima of the preceding 21st and 22nd cycles.
1. Introduction
The elapsing 23rd solar cycle is unique by its duration. It has become the longest (longer than 12.5 years) cycle among all reliably established and studied 11-year solar cycles for more than 150 years of their reliable observations (starting from the 10th cycle). The maximal duration of this cycle additionally confirms the approach of the active descent phase of the 2-secular solar cycle because the duration of an 11-year cycle in whole depends on the phase of a 2-secular solar cycle. Durations of 11-year cycles sequentially increase from the phase of growth to the phases of maximum and descent of a 2-secular cycle [2]. The determination of the exact time of minimum of the ongoing cycle and, consequently, of the beginning of the new 24th solar cycle is becoming more and more topical problem nowadays. The traditional method for the determination of the time of minimum of an 11-year cycle is mostly based on the computation of the sunspot number. Here, the main criterion for the determination of the time of minimum of an 11-year cycle is the minimum of monthly average values of the sunspot number smoothed for 13 months (other criteria are used as well). However the sunspot number does not quantitatively reflect physical aspects of the processes of cyclic variations on the Sun and is practically a conventional qualitative “noisy” parameter. Additionally, during the prolonged and deep minimum of the ongoing 23rd cycle the appearance of sunspots has become a rare event. Due to very low fluctuations of the sunspot number it is becoming an increasingly unreliable quantitative physical parameter for the determination of the time of minimum of the solar cycle (Figure 1). This fact indicates the importance of the search for and introduction of an additional criterion for the determination of the time of minimum of a cycle. The additional criterion should be based on the accurate quantitative measurement of a global parameter of the Sun.
2. The Additional Criterion
Introduction of the additional criterion for the determination of the time of minimum of a solar cycle has become particularly topical due to the upcoming overall descent of the level of the 2-secular cycle, when the amplitude of the sunspot activity variation will sequentially decrease during several subsequent 11-year cycles [1,3,4,6]. Determination of the times of minima of the subsequent cycles (after the 23rd cycle) by the means of traditional method will be less accurate because of a more substantial decrease of the sunspot number and because of its near-zero fluctuation for a long time during the periods of minima of the sunspot activity of these cycles. The uncertainty of determination of the time of minimum of the above cycles can last longer after the minimum takes place. It is known that being the consequences of the same processes occurring deeply inside the Sun, 11-year and 2-secular cyclic variations of the sunspot activity and total solar irradiance (TSI) are synchronized and cross-correlated both in phase and amplitude [1,3]. 11-year cyclic variations of the TSI take place with respect to its 2-secular variation component (dashed line, revealed by us) (Figure 2). By the course of gradient variation of the 2-secular component of the TSI during the minima of three successive cycles one can determine the further course of both TSI and sunspot activity for not only the approaching cycle but also for several subsequent cycles (with somewhat less accuracy) [3].
We propose the use of a high-precision global physical parameter – the minimal level of smoothed TSI variation

Figure 1. Variations of the monthly average values of the TSI (Fröhlich, 2009) and sunspot number (SIDC, 2009) and their values smoothed over 13 months during the period of minimum of the 23rd cycle in 2006-2009
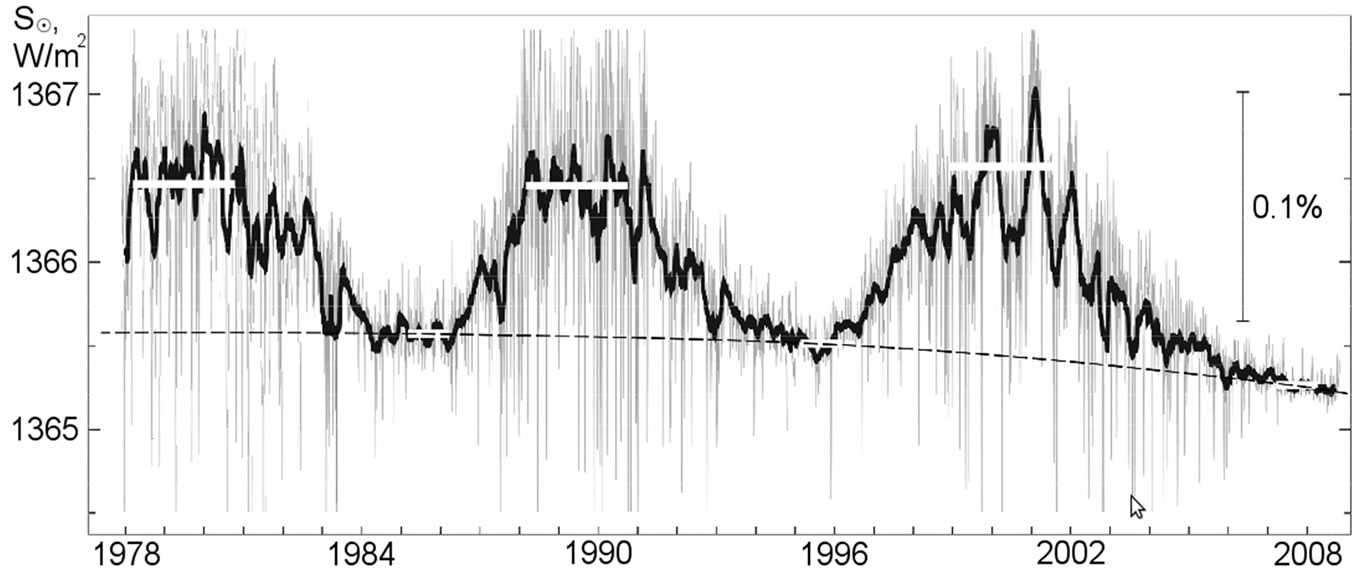
Figure 2. Variations of the TSI over the period from November 16, 1978 to October 24, 2009 (bold line) (Fröhlich, 2009) and of its 2-secular component (dashed line), revealed by us
measured more reliably during the period of minimum of sunspot activity – as an additional criterion for the determination of the time of minimum of a solar cycle. The measured values of the TSI are virtually free of distortions due to the minimal number of sunspots and faculae fields crossing the disc of the Sun during this period. The minimal level of the monthly average values of the TSI smoothed for 13 months when the last two of its values exceed the preceding value at the point of minimum indicates the time of minimum of a cycle. This method involving 13 months smoothing allows one to virtually get rid of the influence of random monthly fluctuations of the TSI which take place due to the transits of small sunspots and small faculae fields across the disc of the Sun during the period of minimum of the cycle.
The given method allows one to determine the time of minimum of a solar cycle with assured reliability. The gradual adoption of 11-month and later 9-month smoothing instead of 13-month will be possible when the direct measurements of the TSI become more reliable and accurate. The proposed additional method for the determination of the time of minimum of a cycle on the basis of the smoothed minimal level of the TSI will provide the possibility of a reliable determination of the dates of these events particularly for the future 11-year cycles which will take place during the phase of descent and minimum of the 2-secular cycle. Here, the smoothed minimal level of the TSI entirely and quantitatively reflects physical aspects of the global cyclic variations of activity of the Sun and is not a practically conventional and more “noisy” qualitative parameter unlike the sunspot numbers.
In order to test the reliability and viability of the proposed method on the basis of the additional criterion we have used it for the determination of the dates of minima of the preceding 21st and 22nd cycles on the basis of the smoothed TSI values and compared them to the dates of these minima determined earlier on the basis of sunspot numbers. For comparison we have plotted the corresponding courses of variations of the monthly average values of the TSI [5], of the sunspot number [7] and of their smoothed values over 13 months during the periods of minima of sunspot activity within the 21st and 22nd cycles (Figures 3 and 4). It has been confirmed that according to the smoothed sunspot number the minimum of the 21st cycle had taken place in September 1986 and the minimum of the 22nd cycle in May 1996. According to the additional criterion based on the smoothed TSI the minimum of the 21st cycle had unambiguously taken place in October 1986 and the minimum of the 22nd cycle in June 1996 (see Table 1). Correlation coefficients between the series of W and TSI smoothed for 13 months near the minima of the 21st, 22nd and 23rd cycles are equal to 0.95, 0.97 and 0.97 respectively.

Table 1. Values of the TSI and sunspot numbers smoothed over 13 months during the minima of the cycles 21-23 and the dates of minima of these cycles determined on the bases of the TSI and sunspot number
The dates of minima determined by the means of the traditional method both in 21st and 22nd cycles lag one month behind the dates determined on the basis of the additional criterion. What is the reason of the mentioned time lag? The lag is observed doubtlessly due to the direct influence of the observed common descent of the TSI. This influence compensates the new 11-year cyclic rise of the TSI within a common (overall) course of observed TSI variation during a certain period of time (the period depends on the gradients of two-secular descent and 11-year rise). This leads to a certain offset (time lag) of the beginning of the new cycle. Anyway, this question deserves further dedicated research partly in order to determine more precisely the duration of the time lag in the descent phase of the two-secular cycle. We suggest that the time of minimum of a cycle determined by the new additional criterion is closer to the truth especially in the period of a deep minimum because it is based on the smoothed quantitative global physical parameter. In the deep minimum of the 23rd cycle in January 2009 the value of TSI smoothed over 13 months reached the record low level of 1365.25 W/m2 which is 0.32 W/m2 and 0.25 W/m2 less, than in the minima of the 21st (October 1986) and 22nd (June 1996) cycles respectively. The smoothed value of the sunspot number in December 2009 also reached the record low level and was equal to 1.7 (see Table 1).
REFERENCES
- H. I. Abdussamatov, “Long-term variations of the integral radiation flux and possible temperature changes in the solar core,” Kinematics and Physics of Celestial Bodies, Vol. 21, No. 6, pp. 328–332, 2005.
- H. I. Abdussamatov, “The time of the end of the current solar cycle and the relationship between duration of 11-year cycles and secular cycle phase,” Kinematics and Physics of Celestial Bodies, Vol. 22, pp. 141–143, 2006.
- H. I. Abdussamatov, “Optimal prediction of the peak of the next 11-year activity cycle and of the peaks of several succeeding cycles on the basis of long-term variations in the solar radius or solar constant,” Kinematics and Physics of Celestial Bodies, Vol. 23, pp. 97–100, 2007.
- S. Duhau, “An early prediction of maximum sunspot number in solar cycle 24,” Solar Physics, Vol. 213, pp. 203–212, 2003.
- C. Fröhlich, “Solar constant,” 2009. http://www.pmodwrc. ch/pmod.php?topic=tsi/composite/SolarConstant
- S. Sello, “Solar cycle activity: A preliminary prediction for cycle 24,” Astronomy and Astrophysics, Vol. 401, pp. 691–693, 2003.
- SIDC (Solar Influences Data Analysis Center), 2009. http://sidc.oma.be/sunspot-data/



