Received 2 June 2015; accepted 7 July 2015; published 10 July 2015

ABSTRACT

The flux of papers from electron positron colliders containing data on the photon structure function 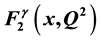ended naturally around 2005. It is thus timely to review the theoretical basis and confront the predictions with a summary of the experimental results. The discussion will focus on the increase of the structure function with x (for x away from the boundaries) and its rise with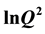, both characteristics being dramatically different from hadronic structure functions. The agreement of the experimental observations with the theoretical calculations is a striking success of QCD. It also allows a new determination of the QCD coupling constant 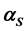which very well corresponds to the values quoted in the literature.

Keywords:

Structure Functions, Photon Structure, Two Photon Physics, QCD, QCD Coupling Constant

1. Historical Introduction

The notion that hadron production in inelastic electron photon scattering can be described in terms of structure functions like in electron nucleon scattering is on first sight surprising because photons are pointlike particles whereas nucleons have a radius of roughly 1 fm. Nevertheless the concept makes sense, not because the photon consists of pions, quarks, gluons etc., but because it couples to other particles and thus can fluctuate e.g. into a quark antiquark pair or a meson. These two basic processes are distinguished by the terms pointlike and hadronic throughout the paper. The idea of a photon fluctuating into a 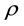meson or other vector mesons was soon applied to estimate the inelastic 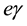scattering cross section in the vector meson dominance model [1] [2] . Calculating the structure function in the quark model [3] then opened the intriguing possibility to investigate experimentally a structure function rising towards large x and showing a distinctive scale breaking because of the proportionality to.

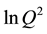Excitement rose after the first calculation of the leading order QCD corrections, because Witten [4] not only calculated the markedly different x dependence of the structure function in QCD but demonstrated that the QCD parameter 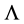could in principle be determined by measuring an absolute cross section quite in contrast to lepton nucleon scattering, where small scale breaking effects in the 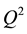evolution of the structure function have to be studied. This “remarkable result” [5] initiated intensive discussions between theorists and experimentalists and passed the first experimental test [6] with flying colors. QCD calculations at next to leading order [7] [8] allowed to give 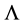a precise meaning in the 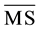renormalization scheme, but also revealed a sickness of the absolute perturbative calculation, producing negative values of 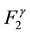near.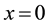

In an invited talk at the 1983 Aachen conference on photon photon collisions [9] , the audience was warned that the implications of these discoveries for the experimental goal of a direct determination of 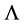from 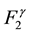were not altogether positive despite “the almost incredible advances on the experimental side”. Instead it was recommended to utilize the 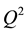evolution like in deep inelastic scattering, a program which was also pursued by other groups [10] .

Ten years later an algebraic error in the original calculation [7] was discovered. Correcting this error [11] [12] squeezed the negative spike near to very small x values where it is of negligible practical importance. For the same reason ad hoc attempts [13] to cure the problem (although still in principle important) proved to be unnecessary for experimental analyses at NLO accuracy.

A new approach to follow the original goal [14] showed promising results. However, based on the results of [15] [16] the structure function for virtual photons was calculated [17] in next-to-next-to-leading-order (NNLO). The findings of this investigation forces one to the conclusion that an absolute prediction for the structure function of real photons is unstable at the three loop level. The concern of the 1980’s is thus still valid, albeit at a higher order in the perturbative series.

2. Basics

Deep-inelastic electron-photon scattering at high energies

(1)

is characterized by a large momentum transfer Q of the scattered electron and a large invariant mass W of the hadrons. The electron energies and in initial and final state combined with the scattering angle define the (negative) momentum transfer squared, , on the electron line with

(2)

and the Bjorken scaling variable x defined as

(3)

are the essential variables for discussing the dynamics of the scattering process as can be seen from the cross section formula corresponding to Figure 1

(4)

which depends on the two structure functions and. Here is a linear combination of, describing the exchange of transversely polarized virtual photons, and

, associated with the exchange of longitudinally polarized virtual photons. The scaling variable y used in the last equation is given by

(5)

(with) and can also be directly calculated from and via

(6)

For QED processes in a region of phase space where one of the muons travels along the

direction of the incoming photon and the other is scattered at large angels (balancing the transverse momentum of the outgoing electron) the structure function has been calculated [11] [18] to be

(7)

with and M denoting the muon mass. The functions and are given by

(8)

(9)

For heavy quarks with three colors, fractional charge e_q and masses the right hand side of Equation (7) has to be multiplied by. Light quarks have current masses with (or at least). Neglecting all terms in Equations (8), (9) and respecting leads for each light quark to the expression

(10)

where is a mass parameter somehow describing the confinement of the light quarks [3] . The QCD parameter can be interpreted as an inverse confinement radius. We therefore replace by and keep in the leading log approximation only terms proportional to resulting in

(11)

as the quark model or zero order QCD expression¹ for the photon structure function if only light quarks are considered.

Using the general quark model relation

(12)

connecting structure function and quark densities one obtains for light quarks the expression

(13)

with

(14)

The factor 2 in Equation (12) accounts for the fact that the photon contains quarks and antiquarks with equal densities but the sum runs over quarks only.

3. QCD Predictions

3.1. Introduction, Leading Order Calculations

The first QCD analysis of the photon structure function [4] based on the operator product expansion (OPE) gave a unified picture of the hadronic and pointlike pieces including gluon radiation in leading order. It was shown that the x and dependence of is unambiguously calculable for asymptotically high values of. Due to the term in front of the pointlike piece this in turn allows for a determination of the strong coupling constant by measuring an absolute cross section. This unique result was later confirmed by calculations using a diagrammatic ansatz [5] and/or solving the Altarelli-Parisi equations [19] [20] like in deep inelastic lepton nucleon scattering (DIS). A modern comprehensive summary of the theoretical foundations has been given by Buras [21] . In this paper we refer to [11] , where the evolution equations for massless quarks (and gluons) are solved in the Mellin n-moment space in leading logarithmic order (LO) and next to leading logarithmic order (NLO).

The nth Mellin moment of a function is defined as

(15)

For example, the quark model function in Equation (14) is projected to

(16)

Like in DIS the quark densities are grouped into two classes described by different evolution equations, flavor non-singlet ( NS) and singlet (S):

(17)

where is the first element of a two component singlet parton density, composed of and the gluon density. Here is the average charge squared in a system with f quark flavors, e.g. for. The connection between structure function and quark densities is in LO defined by

(18)

analogous but not identical to the convention defined by Equation (12). Because of the factor x in Equation (18) the moments of the structure function are related to the moments of the quark densities by

(19)

or with.

We start with a discussion of the LO result for the pointlike, which is given by

(20)

with

(21)

and. The finding of [11] for can be written as

(22)

with

(23)

(24)

and giving the ratio of the strong coupling constant at and the starting point of the evolution. In these equations the effect of gluon radiation on the quark model prediction is cast into a simple form. The quark model term in Equation (22) is multiplied by a factor accounting for the quark quark splitting in the process. The last term in Equation (22) gives a precise meaning to the so called asymptotic solution: becomes independent of and in the limit i.e. for.

Similar (albeit more complicated) relations hold for:

(25)

with

(26)

and

(27)

(28)

The dependence of and on the parameter is not expressed explicitly on the left hand side of Equation (22) and Equation (26). The most important consequence of this dependence is the vanishing of the parton densities at the starting scale because L = 1 at.

All splitting terms required for the evaluation of equations (22) and (26) can be derived from the splitting function moments in [11] (and reference [22] quoted therein) using. Equ- ation (24) above may serve as a check of the normalization used in this paper. The asymptotic solution for can be cast into the compact form [25]

(29)

with

(30)

A very useful combination of the results obtained so far is given by

(31)

where and

(32)

(33)

Setting and all with the quark model result

(34)

with is retained.

The splitting functions (or anomalous dimensions as they are often called following the OPE method) are not restricted to integer n values. For example, the harmonic sum in Equation (24) can be inter- polated with the help of the Digamma function. There are more complicated harmonic sums contained in the other functions and it is even necessary to continue all n dependent functions in equations (22) and (26) into the complex plane in order to invoke the standard method of inverting the Mellin moments by evaluating the integral

(35)

where m is now a continuous complex variable and the contour c has to lie on the right hand side of the rightmost singularity in.

In practice, instead of inverting and the linear combinations

(36)

were chosen because the shape of the corresponding valence and sea distributions in x-space is quite different. The pointlike LO solution in x-space is then given by

(37)

We focus on the asymptotic solution, where and do not depend on and. It was found advantageously to follow the inversion method outlined in [8] , because it quickly leads to analytical ex-

pressions for which can be further used in fitting the data. Using the ansatz

for and the coefficients were determined by fitting the moments of these model functions to and with respectively. The method can easiliy be extended to nonasymptotic solutions by repeating this procedure for any given pair of and.

The results of both inversion methods agree very well, which is demonstrated in Figure 2, where and for and have been plotted. The lines were obtained using functions modeling the moments, whereas the points were calculated by numerically evaluating the integral (35) in the complex plane [24] .

The coefficients necessary for calculating the asymptotic functions and are listed in Table 1(a) for and Table 1(b) for. Note that conventional factors connecting structure functions and quark densities like in Equations (12), (18) have been absorbed in and.

Obviously the LO QCD calculation (37) preserves the behavior of the quark model but changes the x dependence significantly. This is demonstrated in Figure 3 where i.e. the quark model result (11) in units of

(38)

is compared to the evaluation of Equation (37) in units of.

The fact that the behavior of the quark model is preserved, is a consequence of the delicate balance between the increase of the quark population within the photon by the source term and the depletion by gluon radiation which however is damped by the decreasing coupling due to asymptotic freedom. Would the coupling be fixed at a non-zero value [23] , then the gluon radiation would be so strong that asymptotically the parton densities would fall off to zero as a power for any finite value. Thus, the rise of the photon structure function is an exciting consequence of asymptotic freedom in QCD. For the same reason, the quark population is depleted at large x by gluon radiation, and the quarks accumulate at small x. As a result, the photon structure function is strongly tilted―a remarkable prediction of perturbative QCD.

To complete the picture, Figure 3 also contains a QED like variant of the quarkmodel (10) with a log factor instead of. With the curve was calculated for and and then divided by using. The curve is closer to the QCD prediction depending on the new parameter.

Finally a careful inspection of the LO QCD result in Figure 3 reveals a small upward kink beginning at, because increases for. This divergence can be traced back to a pole of (26) when approaches for. These poles which plague the asymptotic perturbative calculations need not concern us as long as they are confined to very small values of x. The full solution has no poles because for

any finite value of L the quotient in Equation (26) remains finite for.

3.2. Next to Leading Order Calculations

In next to leading order the moments of the parton densities are changed, for example Equation (20) reads now

(39)

All NLO effects are contained in thus is the leading order result defined in Equation

(22). A similar relation holds for replacing Equation (25). Besides adding new terms to the parton

densities, in NLO the quark model like relation Equation (19) between structure function and quark densities is also changed. Depending on the factorization scheme used, products of quark densities and the so called Wilson terms have to be added to the right hand side. The lengthy expressions needed to calculate the moments of the structure function in the scheme are again all contained in [11] and [22] . The results can be nicely cast into the form of Equation (31)

(40)

containing all NLO contributions in the last three terms on the right hand side.

For the numerical evaluation we prefer again to regroup all terms according to the valence and sea scheme. After inverting the moments the final equation describing the pointlike solution

(41)

is obtained. The strong coupling constant now has to be evaluated in NLO

(42)

with. For the asymptotic solution the functions, , , can be calculated in a good approximation with the help of Table 1(a), Table 1(b) for. Because and are defined including non leading terms, Equation (41) constitutes in the asymptotic regime an unambiguous QCD prediction depending on one parameter only.

Like in the LO case the structure of Equation (41) does not change if non asymptotic solutions are considered. One has then, however, for each pair of -values first to go through the procedure of calculating and inverting the moments including now explicitly dependent factors like in Equation (22).

Due to the negative correction at the region of high x values is further depleted in NLO as can be seen in Figure 4 where the asymptotic LO and NLO results are compared for and with. At low x values the NLO correction is also negative and would for due to the divergence of even lead to a negative unphysical structure function. This time the divergence is caused by for leading to a pole in which for the asymptotic solution is not compensated by the factor in (40). The resulting spike is confined to very small x-values but is nevertheless of principal importance because it does not allow the calculation of a sum rule for at.

A further example is studied in Figure 5 choosing at and. is positive in the whole domain considered (red curve) with a positive sea term given

by the green curve. Due to an unfortunate algebraic error [7] the moments used in all papers up to

1992 were not correct and resulted in a strongly negative sea term (black curve in Figure 5) which in turn led to a negative pointlike structure function already for [8] i.e. much earlier than in the example of Figure 4. It is not surprising that this finding caused a lot of concern in the literature.

3.3. Master Formula and the Problem of Singularities

As already shown by Witten [4] the moments of the photon structrure function contain besides the pointlike

piece an additional term which in lowest order is written as showing the characteristic hadronic

dependence. The functions can, however, not be calculated perturbatively. Adding the pointlike and hadronic pieces the resulting formula

(43)

determines the moments of the structure function for. The functions are either calculated from a fit to a structure function measured at some low input scale or taken from hadronic models like vector meson dominance (VMD) with an input scale around 0.5 GeV² (see next section). In any case (43) is free of singularities but with the sensitivity to is much reduced. In order to obtain an equation containing an absolute prediction which is sensitive to the QCD scale parameter one has to set in the pointlike part above. Instead of simply doing this by hand we investigate the conditions which allow this procedure.

The pointlike terms can be rewritten as

(44)

The terms proportional to and in the second row showing the typical hadronic dependence can

be combined with the first term in (43) into a new hadronic contribution. The singularities connected

with the term are damped by a factor but can alo be systematically absorbed into the original higher order (h.o.) hadronic terms. We thus find

(45)

In this sum of hadronic terms and the asymptotic solution the new hadronic piece contains divergencies which exactly cancel the divergencies of the asymptotic solution [9] [26] . The basic assumption for comparison with data is then to identify the new hadronic piece for large enough x-values (say) with the VMD parameterization of section 3.4, which is certainly only justified if the spikes are confined to very small x.

We have shown this assumption to be valid for the LO and the NLO calculations. However in NNLO a completely different situation is to be faced. The most dangerous singularities originate now from NNLO terms which have to be added on the right hand side of (45). As an example we study the behaviour of which for approaches 1 for n = 6.0445. In the vicinity of the pole at we write

(46)

which leads in x-space to a divergent term. The coefficient c can be estimated from table II of [17] . Using we get resulting after multiplication with in a contribution

to the structure function at small x. This huge singularity is obviously not confined to small x-values and makes (together with additional singularities) the prediction of the asymptotic un- reliable.

The principal problem of the poles of, and in the LO, NLO and NNLO eva-

luation of is known since long [27] . But only after the necessary explicit three loop QCD calculations had been performed [15] [16] [28] it became clear that the residues of the NNLO-poles are not small enough to avoid a contamination of the large x-region. Consequently only the full pointlike solution (starting at) has been calculated beyond the next to leading order [28] .

3.4. Modelling the Hadroncic Piece of

The coupling of the photon to the final-state hadrons is mediated by quarks and antiquarks. If the transverse momentum in the splitting process is small, quark and antiquark travel for a large distance almost parallel with the same velocity so that strong interactions can develop and bound states form eventually. Associating a light vector meson with this hadronic quantum fluctuation, the corresponding com- ponent of the photon wave-function is described by

(47)

which is identical to the vector meson dominance (VMD) ansatz describing the hadronic nature of the photon

(48)

if the photon vector meson couplings are taken from the quark model neglecting mass effects. Preferring the measured couplings as determined from the partial decay width and utilizing isospin invariance [30] has been tied to the well known pionic quark densities which are available in an easy to use parameterization [30] .

The result for is shown in Figure 6 for. Above there is little variation with Q² whereas below the sharp increase already indicates a tendency to cancel negative spikes in. It is interesting to see, how close a simple straight line approaches the results of the complicated evolution model at. Straight line models of this sort have been used in the early experimental papers [31] .

4. Two Photon Kinematics

Experiments measuring the photon structure function have until now only been performed at storage rings. The reaction

(49)

is dominated by the so called two photon diagram shown in Figure 7 which also includes some kinematical definitions. Originally these reactions have been considered only as a background to annihilation

but became, due to the absence of high energetic real photon beams, the only source of direct experimental information about.

The incoming leptons in Figure 7 radiate virtual photons with four momenta producing a hadronic

system X with an invariant mass The sixfold differential cross section is given

by a complicated combination of kinematical factors and six in principle unknown hadronic functions (four cross sections and two interference terms) depending on. The general formalism has been discussed in great detail in [18] , for a recent review and extension see [32] . The paper of Budnev et al. [18] served as the basis of all experimental analyses.

In the limit which is realized by very small forward scattering angles of one of the incoming leptons (e.g. the positron) the relevant formulae are greatly simplified and the cross section reads

(50)

with

(51)

(52)

and

(53)

where the definition has been used.

The two photon cross sections and depend on and. The indices represent the transverse (T) and longitudinal (L) polarization of the virtual photons. The physical interpretation of these equations is like follows: the incoming positron is replaced by a beam of quasi real photons with transverse polarization traveling along the positron direction. The number of photons in the energy interval is given by. The term denotes the number of transversely polarized photons radiated from the electron scattered into the solid angle and energy interval at angles. With the help of the polarization parameter the number of longitudinal photons is given by. A very useful feature of this formalism is the factorization of the flux factors into and where and depend on electron variables and on positron variables only. This allows for a considerable simplification calculating the photon fluxes in Monte Carlo routines simulating the experiments. It has been shown [33] that for mrad the numerical difference in evaluating the incoming photon densities from this approach or from the exact formula [18] is less than 0.5% for.

Replacing the cross sections by the structure functions

(54)

we arrive after a change of variables at

(55)

which corresponds to Equation (4) multiplied by the spectral density of the incoming photons. Under actual experimental conditions, y is quite small in general, so that is very difficult to measure. Experiments usually focus on the measurement of and neglect. This is theoretically backed further by the fact that quark model and QCD predict to be the leading component.

The standard expression (53) has first been derived by Kessler [34] . In the spirit of the leading log appro- ximation it can be replaced by

(56)

useful for rough estimates of the counting rate. One has, however, to keep in mind that neglecting the cutoff has not only numerical consequences, but quickly violates the basic assumption. It is difficult to quote unambiguous limits for the maximum allowed mean values. Detailed calculation of pair production [35] revealed that for and mrad one has and 97% of the cross section is contained in Equation (50), a result which is likely also to be valid for the quark model and QCD. It follows that the experiments need forward spectrometers with electromagnetic calorimeters very close to the beam pipe which allow to reject positrons with angles larger than about 25 mrad via the method of antitagging.

The basic experimental procedure is thus given by investigating the reaction with the electron scattered at angles larger than and the positron traveling undetected down the beam pipe (and vice versa). Due to the unknown energy of the outgoing positron is also not known and the usual relation cannot be used for calculating x. Therefore hadronic calorimeters reaching down to small forward scattering angles are needed in order to measure the invariant mass W of the produced hadronic system and calculate x from Equation (3). Unfortunately the remnants of the antiquark in Figure 1 will also be dominantly concentrated at small angles and losses in the hadronic energy are unavoidable. With sophisticated unfolding methods have to be employed in order to reconstruct x. These methods are described in the experimental publications and reviewed in [26] and [35] . A discussion of the various Monte Carlo routines used by the different experimental groups in evaluating the cross section can e.g. be found in [35] .

5. Experimental Analysis

Following the pioneering work of the PLUTO collaboration [6] many experiments have been performed at all high energy storage rings. In order to avoid the region of small x with its mixture of correlated hadronic and pointlike contributions we exclude data with. Data where the charm component has been subtracted and all data published in conference proceedings only are also discarded. Only the most recent publication of statistically overlapping data of the same collaboration was accepted. This selection leads to 109 experimental values of with values ranging from 4.3 GeV² to 780 GeV² from the collaborations ALEPH [36] [37] , AMY [38] [39] , DELPHI [40] , JADE [41] , L3 [42] - [45] , OPAL [46] - [48] , PLUTO [31] [49] , TASSO [50] , TOPAZ [51] and TPC/2g [52] . In cases where the experimental uncertainties could only be read off the figures the tables of Nisius [35] were used. As usual the experimental x and values are obtained from an averaging procedure over the sometimes rather large x and bins. In most cases x coincides with the bin center.

After the 1980 crisis of the perturbative calculation most QCD analyses were performed like in deep inelastic scattering by comparing the data to models obtained by evolving the parton densities from a starting scale up to. For a recent extensive study see [53] . On the other hands side data at high and high x (defined by and) were fitted to the asymptotic pointlike solution (41) for, supplemented by the quark model formula (7) for a charm quark with mass 1.5 GeV [14] . The fit described the data very well and resulted in with for 20 experimental data.

Here we follow a more radical approach and fit the whole sample of 109 data sets to a model whose three components have been discussed in the previous sections:

1) The pointlike asymptotic NLO QCD prediction for 3 light flavors in the scheme with as the only free parameter using the coefficients of Table 1(a).

2) A quark model calculation of the charm and bottom quark contribution using Equation (7) multiplied by. Applying the scheme for the light quark QCD calculation it is only natural to use the masses and as quoted by the Particle Data Group [54] .

3) A detailed parameterization (VMD) for the hadronic part of the structure function [30] including the evolution. Examples for different values of are displayed in Figure 6.

Fitting the data with this model results in a value of. The quality of the fit, mea- sured in terms of the value per degree of freedom, is given by. A value slightly below unity is probably explained by the neglect of bin to bin correlations in the fitting procedure. These correlations were only given in six of the seventeen experimental publications used.

Following the method explained in [55] is converted to and therefore is obtained in NLO where the error only reflects the experimental uncertainties. In order to estimate the theoretical error we first neglected the bottom quark contribution which changes by a very small amount (0.0002). Varying within the quoted error of resulted in . The most important source of theoretical uncertainty is the treatment of the hadronic contri- bution. This error is hard to estimate. Possible interferences between hadronic and pointlike part are very likely restricted to the region which is excluded by our data selection. The authors of [29] emphasize the very good agreement of their result with pionic and photonic structure function data. Assuming a 10% normalization error for yields. Adding all errors in quadrature the final result is

(57)

which agrees nicely with the DIS average and the world average as given in [54] [56] .

In order to visualize the impressive agreement between data and theory two examples are presented. In Figure 8 the PLUTO data [31] at 4.3 GeV² (black crosses) and the OPAL data [48] at 39.7 GeV² (blue crosses) are compared with our model. The data clearly do not follow the typical mesonic dependence and also demonstrate implicitly the rather strong dependence predicted by QCD.

Next the dependence of is directly tested by selecting data with. The average x value was determined taking the mean value of the x intervals quoted in the experimental papers. The 36 data sets are grouped in bins with equal bin width in. Each value is then shifted to the center of the corresponding bin using the theoretical model and the weighted average of all data within the bin is calculated. The result is shown in Figure 9 together with the theoretical curve calculated for. The increase of the data with is clearly seen, especially in contrast to the well known slight decrease of the proton structure function for between Q² = 5 and 800 GeV². Neglecting the small dependence of the hadronic

piece the theoretical model can in LO be written as. A fit of the data in

Figure 9 according to this ansatz yields thus establishing numerically the predicted increase with beyond any doubt. This value agrees very well with the earlier analysis of [35] .

6. Virtual Photon Structure

The perturbative calculations have been extended to the region [57] [58] which is experi- mentally accessible requesting also the positron being scattered into finite angles (double tagging). Regarding the theory one has in the formalism of [11] simply to replace the parameter by the variable for the cal- culation of in LO. Ueamtsu and Walsh [58] emphasized that for virtual photons also the hadronic piece is perturbatively calculable. The required additional terms are given in [17] [58] .

Gluon radiation is efficiently suppressed for virtual photons, thus moving closer to the quark

model result. Analytically this can be proven easily [57] by investigating the LO order solution, e.g., Equation (20). Because in LO is proportional to we have

(58)

Using the nominator reduces in the limit to. Since a similar relation holds for the singlet term, the final result² is

(59)

i.e. the quark model formula (34) with the log factor replaced by. As an illustration the LO prediction for, and is compared in Figure 10 with Equation (59) showing perfect agreement at small and medium x values. The parameter free QCD prediction (59) is, however, difficult to be tested experimentally because with the present value of the condition

can hardly be achieved.

Regarding the determination of from the measured cross section, it should be remembered

that the virtual photon photon scattering is in general described by four cross sections and two interference terms

(see Section IV). After proper integration over the interference terms the cross section formula of [18] can be written as

(60)

where the factor is approximately interpreted as describing the fluxes of transverse virtual photons from the incoming electron and positron. The polarization parameters and are for typical experimental con- ditions close to 1 and therefore

(61)

The relation between structure functions and cross sections is more complicated than discussed above for electron scattering off real photons. In the limit the general formulae given in [26] reduce to

(62)

using and. Defining an effective structure function via

(63)

one gets finally

(64)

Experimental data is scarce. The first results of the PLUTO collaboration [60] at and (black crosses in Figure 11) were only followed by data of the L3 collaboration [44] at and (blue crosses in Figure 11).

For comparison with theory is calculated in NLO for 3 flavors choosing. According to Equation (64) cannot be neglected. The longitudinal structure function of real photons is extensively discussed in the literature [59] . For virtual photons has been calculated in

LO and NLO [17] [58] . Here we combine the LO result with the NLO calculation of the pointlike and hadronic terms. The charm quark contribution for and is taken from the quark model result for real photons as recommended in [29] . Because the PLUTO data are taken at a value close to the real photon case a VMD

part was added multiplied by a form factor where is the meson mass. Using this

form factor the VMD term is reduced by a factor 2.5 and thus for the sake of simplicity the straight line model is applied improving somehow the agreement with the data at low x. Altogether the red curve (PLUTO) and the green curve (L3) in Figure 11 are in very good agreement with the data although admittedly this is not a very decisive test due to the large experimental errors. A comparison including the rather small NNLO corrections can be found in [63] .

7. Conclusions

Measurements of the photon structure function taken at colliders were confronted with theoretical models. For real photons the main component is the fixed flavor NLO asymptotic QCD result in the scheme as given in Equation (41) evaluated with the functions of Table 1. This part is complemented by charm and bottom heavy quark contributions calculated in the quark model and by a hadronic contribution taken from vector meson dominance. The model describes not only the x and distributions very well but also allows for a precise determination of the strong coupling constant, yielding. As explained above, the treatment of the hadronic and the heavy quark contribution to does not follow from first principles but is based on model assumptions. The validity of these assumptions is supported by the observation that using the standard model value of the selected data are described by the model of Section 5 with. Finally the few available data for virtual photons agree well with the QCD predictions.

New experimental input can only be expected from a new high energy collider. At the planned linear collider ILC [61] it is in principle possible to install a high intensity beam of real photons via backscattering of laser light. This would for the first time allow to study inelastic electron photon scattering in a beam of real pho- tons with a spectrum and intensity far superior to the virtual photons used until now [62] . In addition nagging doubts about the P² cutoff in some of the two photon experiments are baseless in such an environment.

Acknowledgements

First of all, I want to thank P.M. Zerwas for his constant support and the many discussions concerning the theoretical basis. I am very grateful for the help I got from R. Nisius. Useful conversations with M. Klasen are also gratefully acknowledged.

Cite this paper

ChristophBerger, (2015) Photon Structure Function Revisited. Journal of Modern Physics,06,1023-1043. doi: 10.4236/jmp.2015.68107

References