Received 14 May 2015; accepted 21 November 2015; published 24 November 2015

ABSTRACT

We show that the lateral regularizations of the generator of any uniformly bounded set-valued composition Nemytskij operator acting in the spaces of functions of bounded variation in the sense of Riesz, with nonempty bounded closed and convex values, are an affine function.

Keywords:

j-Variation in the Sense of Riesz, Set-Valued Functions, Left and Right Regularizations, Uniformly Bounded Operator, Composition (Nemytskij) Operator, Jensen Equation

1. Introduction

Let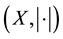, be real normed spaces, C be a convex cone in X and I be an arbitrary real interval. Let 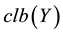denote the family of all non-empty bounded, closed and convex subsets of Y. For a given set-valued

function 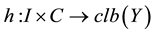we consider the composition (superposition) Nemytskij operator defined by 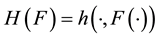for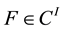. It is shown that if H maps the space 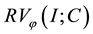of function of bounded j-variation in the sense of Riesz into the space 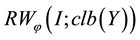of closed bounded convex valued functions of bounded y-variation in the sense of Riesz, and H is uniformly bounded, then the one-side regularizations 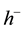and 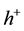of h with respect to the first variable exist and are affine with respect to the second variable. In particular,

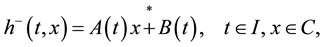(1)

for some functions 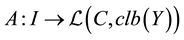and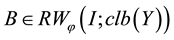, where stands for the space of all linear mappings acting from C into. This considerably extends the main result of the paper [1] where the uniform continuity of the operator H is assumed.

The first paper concerning composition operators in the space of bounded variation functions was written by J. Miś and J. Matkowski in 1984 [2] ; these results shown here have been verified by varying the hypothesis, in other contributions (see for example, [1] [3] - [7] ).

Let us remark that the uniform boundedness of an operator (weaker than the usual boundedness) was introduced and applied in [8] for the Nemytskij composition operators acting between spaces of Hölder functions in the single-valued case and then extended to the set-valued cases in [6] for the operator with convex and compact values, in [7] for the operators with convex and closed values, and also, in [4] for the Nemytskij operator in the spaces of functions of bounded variation in the sense of Wiener.

Some ideas due to W. Smajdor [9] and her co-workers [10] [11] , V. Chistyakov [12] , as well as J. Matkoswki and M. Wróbel [6] [7] are applied.

The motivation for our work is due to the results of T. Ereú et al. [3] and Głazowska et al. [4] , but only that our research is developed for some functions of bounded j-variation in the sense of Riesz.

2. Preliminaries

Let be the set of all convex functions such that and for.

Remark 2.1. If, then is continuous and strictly increasing. An usually, stands for the set of all functions.

Definition 2.2. Let and be a normed space. A function is of bounded j-variation in the sense of Riesz in the interval I, if

(2)

where the supremum is taken over all finite and increasing sequences, ,.

For condition 2 coincide with the classical concept of variation in the sense of Jordan [13] when, and in the sense of Riesz [14] if. The general Definition 2.2 was introduced by Medvedev [15] .

Denote by the set of all functions such that for some. is a normed space endowed with the norm

(3)

where and.

For the linear normed space was studied by Ciemnoczołowski and Orlicz [16] and Merentes et al. [5] . The functional is called Luxemburg-Nakano-Orlicz seminorm (see [17] -[19] ).

Let be a normed real vector space. Denote by the family of all nonempty closed bounded convex subset of Y equipped with the Hausdorff metric D generated by the norm in Y:

(4)

Given, we put and we introduce the operation in defined as follows:

(5)

where stands for the closure in Y. The class with the operation is an Abelian semigroup, with {0} as the zero element, which satisfies the cancelation law. Moreover, we can multiply elements of by nonnegative number and, for all and, the following conditions hold:

(6)

Since,

(7)

is an abstract convex cone, and this cone is complete provided Y is a Banach space (cf. [9] [12] [20] ).

Definition 2.3. Let and. We say that F has bounded j variation in the sense of Riesz, if

(8)

where the supremum is taken over all finite and increasing sequences, ,.

Let

(9)

For put

(10)

where

(11)

and

(12)

where the supremum is taken over all finite and increasing sequences.

Lemma 2.4. ([12] , Lemma 4.1 (c)) The and. Then for

(13)

Let, be two real normed spaces. A subset is said to be a convex cone if for all and. It is obvious that. Given a set-valued function we consider the composition operator generated by h, i.e.,

(14)

A set-valued function is said to be ^*additive, if

(15)

and ^*Jensen if

(16)

The following lemma was established for operators C with compact convex values in Y by Fifer ( [21] , Theorem 2) (if) and Nikodem ( [22] , Theorem 5.6) (if K is a cone). An abstract version of this lemma is due to W. Smajdor ( [9] , Theorem 1). We will need the following result:

Lemma 2.5. ([12] , Lemma 12.2) Let C be a convex cone be in a real linear space and let be a Banach space. A set-valued function is ^*Jensen, if and only if, there exists an ^*additive set-valued function and a set such that

(17)

for all.

For the normed spaces, by, briefly, we denote the normed space of all additive and continuous mappings.

Let C be a convex cone in a real normed space. From now on, let the set consists of all set-valued function which are ^*additive and continuous (so positively homogeneous), i.e.,

(18)

The set can be equipped with the metric defined by

(19)

3. Some Results and Its Consequences

For a set, we put

(20)

Theorem 3.1. Let be a real normed space, a real Banach space, a convex cone, an arbitrary interval and let. Suppose that set-valued function is such that, for any the function is continuous with respect to the second variable. If the composition operator H generated by the set-valued function h maps into, and satisfies the inequality

(21)

for some function, then the left and right regularizations of h, i.e., the functions and defined by

exist and

for some functions, , and , where, , and.

Proof. For every, the constant function, belongs to. Since H maps into, the function belongs to. By

( [12] , Theorem 4.2), the completeness of with respect to the Hausdorff metric implies the existence of the left regularization of h. Since H satisfies the inequality (21), by definition of the metric, we obtain

(22)

According to Lemma 2.4, if, the inequality (22) is equivalent to

(23)

Therefore, if, , , , the definitions of the operator H and the functional, imply

(24)

For, we define the function by

(25)

Let us fix. For an arbitrary finite sequence and , the functions defined by

(26)

belongs to the space. It is easy to verify that

whence

and, moreover

Applying (24) for the functions and we get:

(27)

All this technique is based on [12] . From the continuity of and the definition of, passing to the limit in (27) when, we obtain that

(28)

that is

(29)

Hence, since is arbitrary, we get,

and, as only if, we obtain

Therefore

(30)

for all and all.

Thus, for each, the set-valued function satisfies the ^*Jensen functional equation.

Consequently, by Lemma 2.5, for every there exist an ^*additive set--valued function and a set such that

(31)

which proves the first part of our result.

To show that is continuous for any, let us fix. By (7) and (31) we have

(32)

Hence, the continuity of h with respect to the second variable implies the continuity of and, consequently, being ^*additive, for every. To prove that let us note that the ^*additivity of implies. Therefore, putting in (31) we get

(33)

which gives the required claim.

The representation of the right regularization can be obtained in a similar way.

Remark 3.2. If the function is right continuous at 0 and, then the assumption of the continuity of h with respect to the second variable can be omitted, as it follows from (2).

Note that in the first part of the Theorem 3.1 the function is completely arbitrary.

As in immediate consequence of Theorem 3.1 we obtain the following corollary Lemma 3.3.

Lemma 3.3. Let be a real normed space, a real Banach space, C a convex cone in X and suppose that. If the composition operator H generated by a set-valued function maps into, and there exists a function right continuous at 0 with, such that

(34)

then

for some, , and.

4. Uniformly Bounded Composition Operator

Definition 4.1. ([8] , Definition 1) Let X and Y be two metric (normed) spaces. We say that a mapping is uniformly bounded if for any there is a real number such that for any nonempty set we have

(35)

Remark 4.2. Obviously, every uniformly continuous operator or Lipschitzian operator is uniformly bounded. Note that, under the assumptions of this definition, every bounded operator is uniformly bounded.

The main result of this paper reads as follows:

Theorem 4.3. Let be a real normed space, be a real Banach space, be a convex cone, be an arbitrary interval and suppose. If the composition operator generated by a set-valued function maps into, and is uniformly bounded, then

for some functions, , and , where, , and.

Proof. Take any and arbitrary such that

(36)

Since, by the uniform boundedness of H, we have

(37)

that is

(38)

and the result follows from Theorem 3.1.

Acknowledgements

The author would like to thank the anonymous referee and the editors for their valuable comments and suggestions. Also, Wadie Aziz want to mention this research was partly supported by CDCHTA of Universidad de Los Andes under the project NURR-C-584-15-05-B.

Cite this paper

WadieAziz,NelsonMerentes, (2015) Uniformly Bounded Set-Valued Composition Operators in the Spaces of Functions of Bounded Variation in the Sense of Riesz. International Journal of Modern Nonlinear Theory and Application,04,226-233. doi: 10.4236/ijmnta.2015.44017

References