Open Journal of Acoustics
Vol.3 No.4(2013), Article ID:40571,7 pages DOI:10.4236/oja.2013.34016
The Scattering of a Cylindrical Shear-Axial Wave by a Circular Cavity in Piezoelectric Crystal
Sarov Physics Technical Institute of National Nuclear Research University, Sarov, Russia.
Email: ns_shev@mail.ru
Copyright © 2013 Evgenij Kosyak, Nikolaj Shevyakhov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 20, 2013; revised October 20, 2013; accepted October 27, 2013
Keywords: diffraction; scattering indicatrix; section of scattering; piezoeffect
ABSTRACT
The features of a cylindrical shear-axial wave scattering by a circular cavity in piezoelectric crystal of 6(4)-class of symmetry are discussed. It is shown that the basic integral characteristics of scattering—scattering indicatrix and total cross-section scattering have large changes with approach of a linear shear-axial wave source to cavity boundary. The small-scale oscillations in spectra of scattering are caused by the interference contribution of waves circulating on a boundary as they are capable of effective capture by concave metallized boundary of a cavity.
1. Introduction
The scattering of a plane monochromatic shear wave by cylindrical inсlusion in piezoelectric crystal was a subject of discussion in works of one of the authors [1-4]. Main influence of conductivity and azimuthal drift of charge carriers in the semi-conductor cylinder placed in a cavity on partial waves of a scattering field and changes of the amplitude characteristic of scattering (scattering indicatrix) connected with it in a far-wave zone was considered in [1,2]. In works [3,4] the attention was paid to changes of total cross-section scattering of a plane shear wave by a cavity in piezoelectric crystal due to piezoeffect. The purpose of our investigation is the subsequent generalization of these results on the case, when the incident shear harmonic wave doesn’t have plane, but cylindrical front. In other words wave oscillations are propagating from a linear source of shear-axial radiation located in piezoelectric crystal on restricted distance from a cavity.
Some academism of statement of the research problem is aggravated, certainly, by the circumstance which is against works [1-4], where the plane shear wave could be considered as idealization of radiation of a shear wave source, located on an external surface of a crystal (a situation, typical in experimental practice). Here, linear source of radiation is located in the volume of a crystal. It is known, however, [5] and it is confirmed experimentally [6] that cylindrical pulses of acoustic radiation arise in crystals in the process of dislocation annihilation. In particular, at annihilation of pair parallel screw dislocations of opposite signs, the pulse of divergent cylindrical shear waves is formed [5]. Thus, our investigation of features of a cylindrical shear wave scattering by a circular cavity in piezoelectric crystal besides general theoretical interest can be useful to mathematical modeling of the acoustic emission phenomena in crystals with piezoeffect.
2. Formulation and the Solution of a Boundary Problem
Let us consider the piezoelectric crystal of 6 (4, 6 mm, 4 mm, ¥ mm) class symmetry with a cavity of circular section of radius R, which axis z coincides with the high order 6 (4) axis of crystal symmetry. We assume too, that cavity is filled with strongly rarefied gas (air); ec is the permittivity of gas. If the shear waves have axial polarization of displacement u||z, the crystal, occupying in cylindrical coordinates (r, q, z), area r > R, it is enough to characterize by longitudinal e15 and cross e14 coefficients of piezoelectricity, module of shear l, density r and permittivity e. Then connected electroelastic field in piezoelectric crystal may be found in quasi-static approach from the decision of the following system of the equations [3].
 ,
, 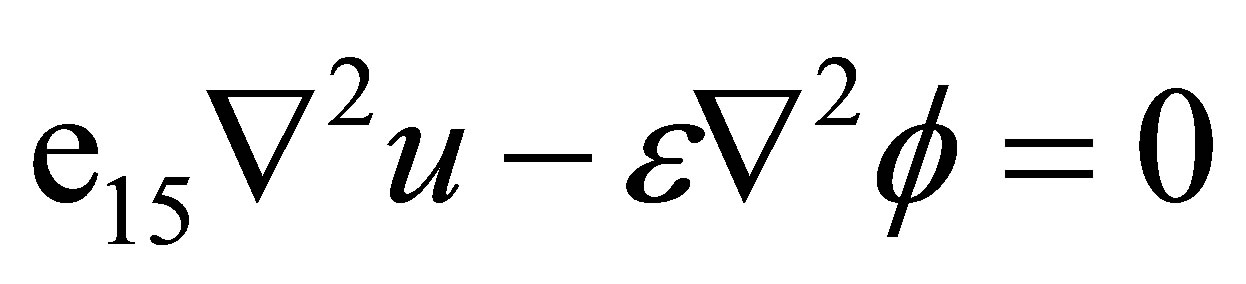 , (1)
, (1)
where u is the shear-axial displacement,
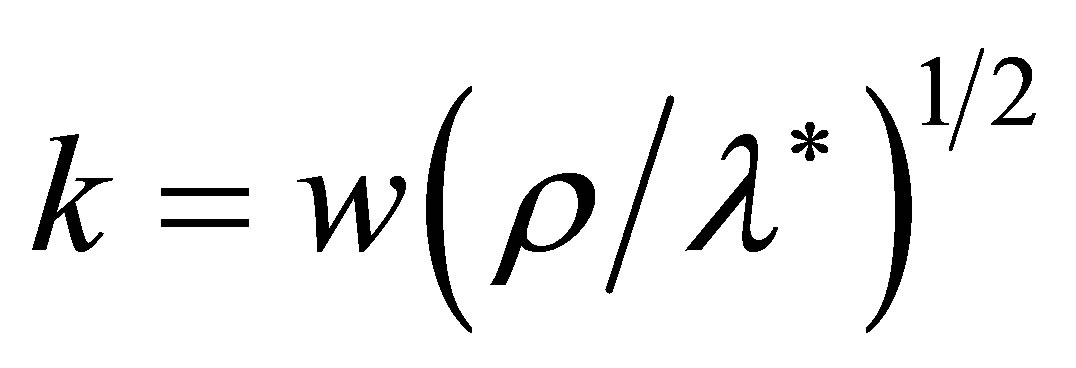
is the wave number, 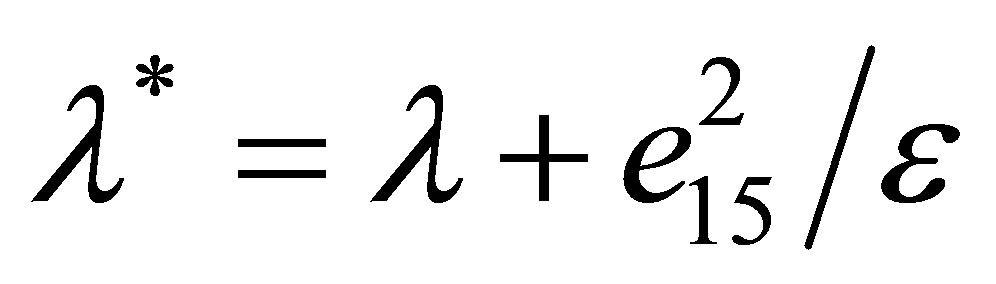 is the shear module with correction on piezoelectricity,
is the shear module with correction on piezoelectricity,  is Laplacian operator in plane x0y, j is the electric potential.
is Laplacian operator in plane x0y, j is the electric potential.
equations (1) should be considered together with the equation
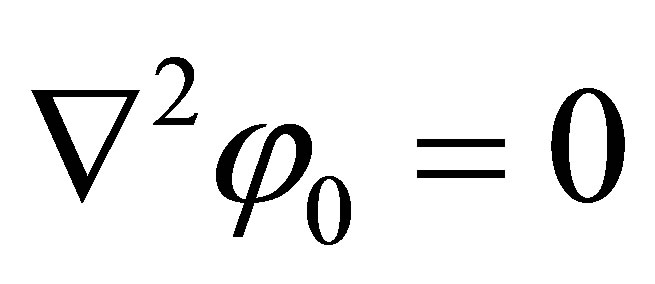 (2)
(2)
for the potential j0 of electrical field in a cavity. It may be noticed, that the second of equations (1) allows to present potential j as
 . (3)
. (3)
Here F is the potential of near-boundary electrical oscillations in piezoelectric crystal, satisfying as j0 to Laplace equation. Linear harmonic source of a cylindrical shear-axial wave of the given amplitude U and frequencies w we shall arrange (see Figure 1) in parallel axes of a cavity on distance d > R from it along a radial direction with the azimuth q = p. Let us designate as a the corner between a polar direction O1Ox and direction on observation point M from a source and as l the distance from a source up to the observation point.
The field of shear displacement u in the expression (3) we shall present as the sum
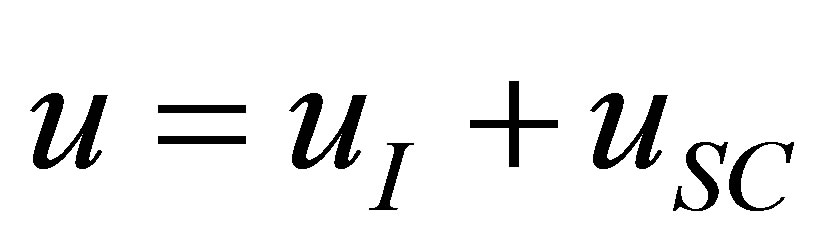 . (4)
. (4)
The members, included in it, are the decisions of the Helmholtz equation (1), representing accordingly the radiation field uI of a linear harmonic source O1 and the field of shear waves uSC, scattering by a cavity (radiated by a virtual source O). By a principle of ultimate absorption we have in coordinates of each source
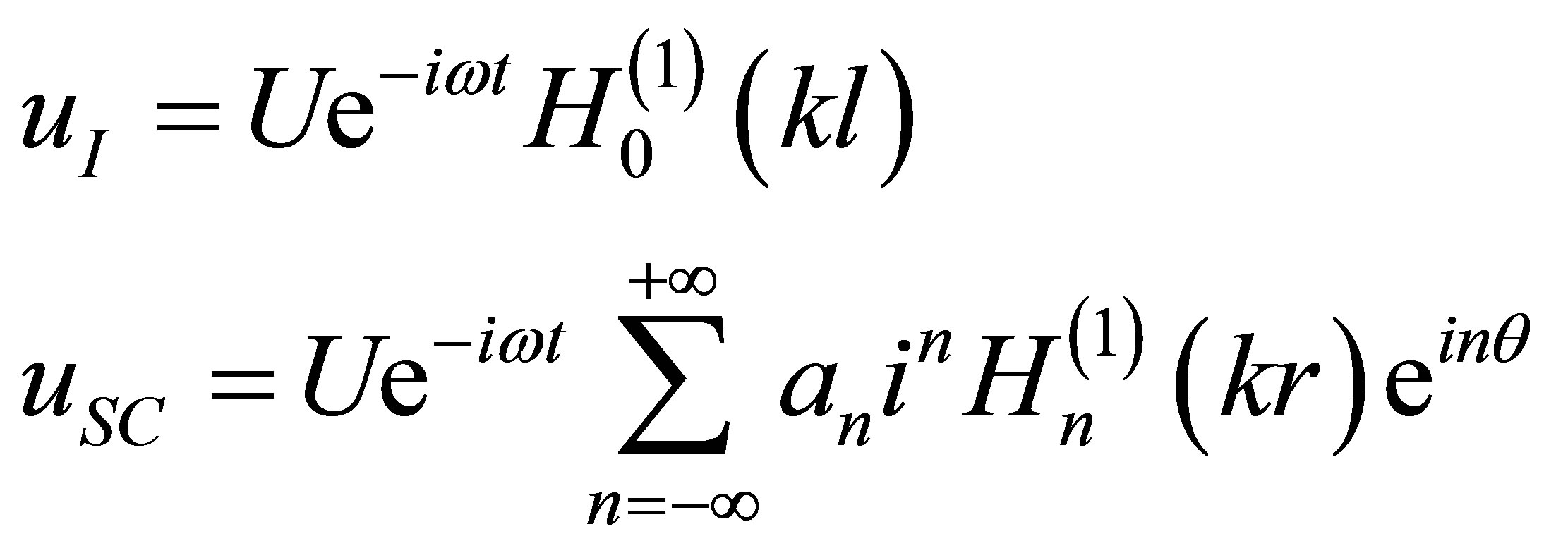 . (5)
. (5)
Here t is the time,  is the first kind Hankel function of integer order
is the first kind Hankel function of integer order  [7], an is the amplitude factors of partial waves, scattering by a cavity.
[7], an is the amplitude factors of partial waves, scattering by a cavity.
Potentials F and j0, as the decisions of Laplace equations, results from scattering of the cylindrical wave (5) by a cylindrical cavity and, therefore, it is natural to express them in coordinates of a cylindrical cavity by the following sums of partial azimuthal harmonics
 (6)
(6)
with some coefficients bn and cn, which are found from

Figure 1. Geometry of the problem. The concentric dashed circles represent fronts of a divergent shear-axial wave, emitted by a harmonic source O1.
the boundary conditions. Ones express the absence of shear stress Trz and the continuity of potentials and radial components of electric induction on the boundary r = R.
To satisfy with above mention conditions on the boundary of a cavity, it is necessary also to write a radiation field of a linear source uI (5) in coordinates (r, q). With this purpose we shall use the addition theorem for cylindrical functions [7]—the method, which is often done at the solution of scattering problems with linear sources of radiation [8,9]. For represented on a figure 1 triangle O1OM of pair of cylindrical coordinates with the parallel axes O1 and O, displaced in polar direction, any point of boundary r = R satisfies to the condition r < d. Suitable on a reason of convergence of cylindrical functions expansion there will be, therefore, the following form of the addition theorem:
 . (7)
. (7)
In that formula Zn(x) is any cylindrical function.
With the account (7), equality
and properties of cylindrical functions [7], the field of shear displacement u, after simple manipulations similarly made in [8,9], can to represent in a form
 (8)
(8)
Comparing the expression (8) with a field arising at the scattering of a plane monochromatic shear wave, when the linear source O1 is removed in infinity (d ® ¥) [3]
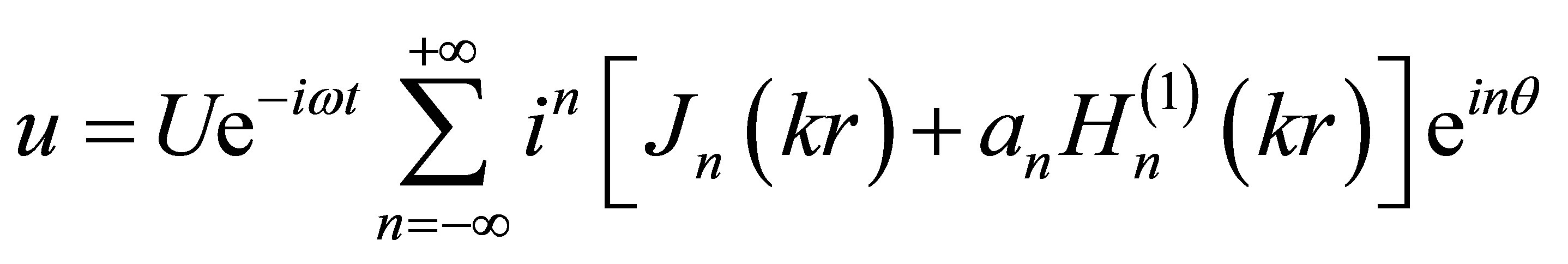 , (9)
, (9)
it is possible to notice, that the difference of amplitude coefficients
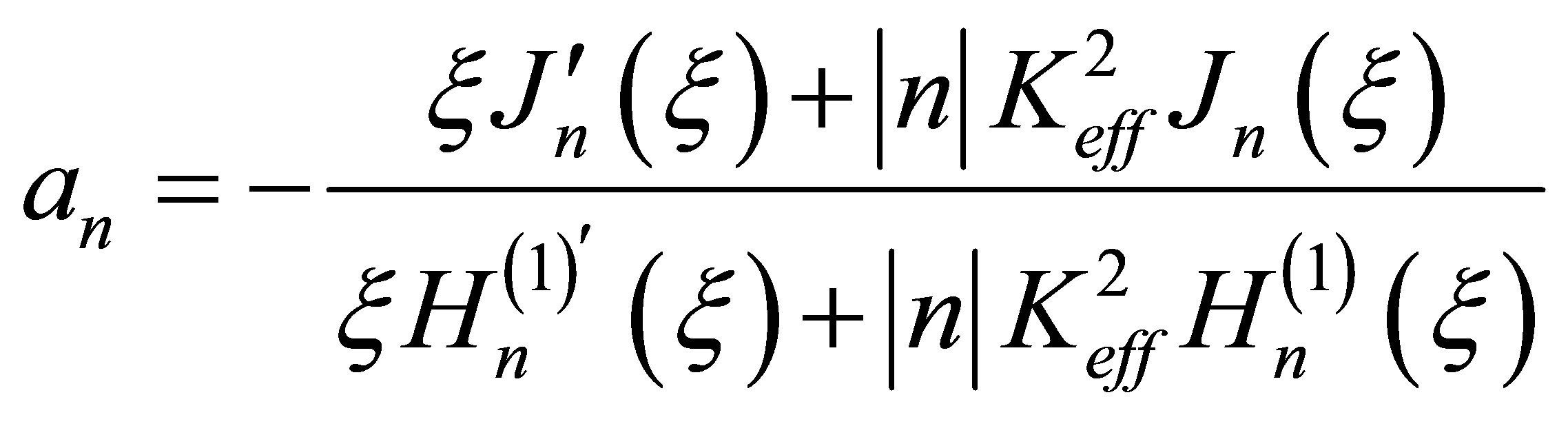 , (10)
, (10)
which were found in work [3], from the amplitude coefficients of a considered boundary problem of a cylindrical wave scattering by a circular cavity in piezoelectric crystal, will be shown in (10) extremely by addition of factor
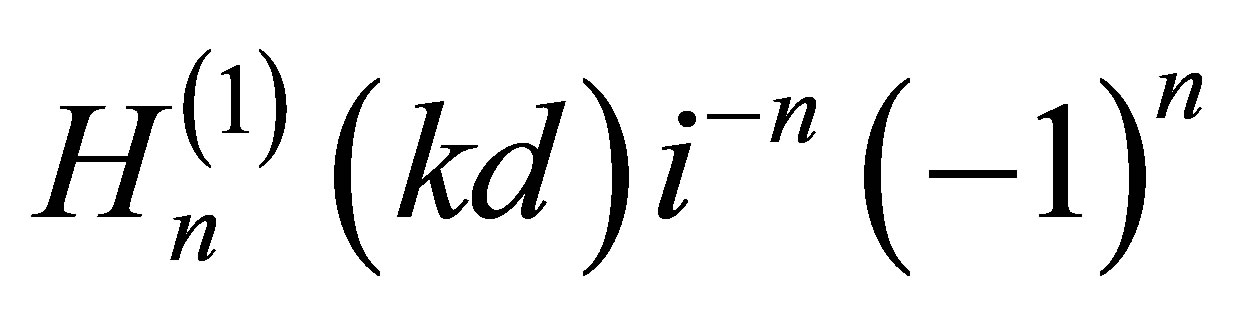
before Bessel function

and its derivative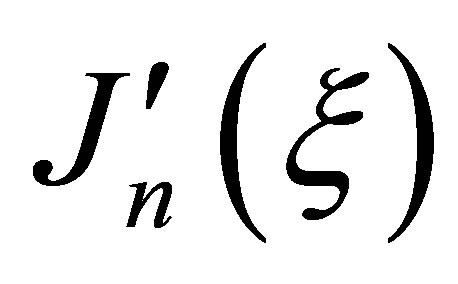 . Thus, we shall receive
. Thus, we shall receive
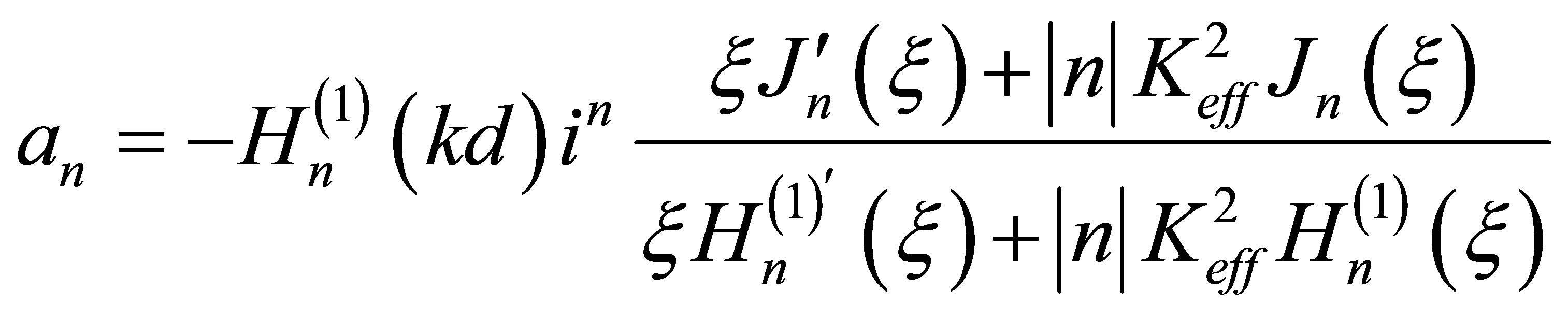 . (11)
. (11)
In formula (11) the value
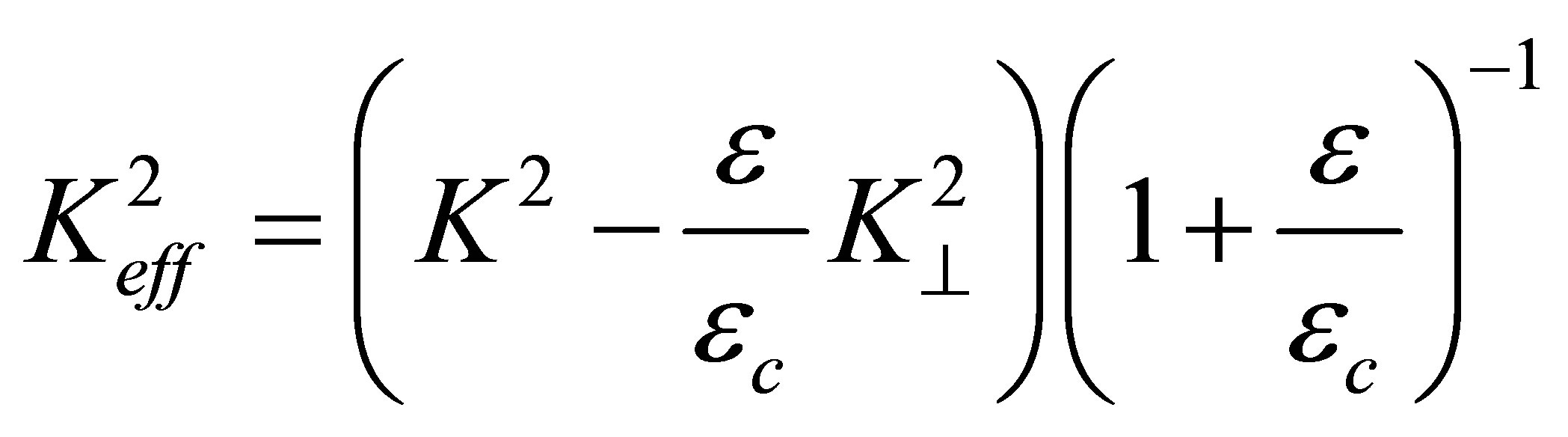 (12)
(12)
is square of the effective electromechanical coupling coefficient and the values
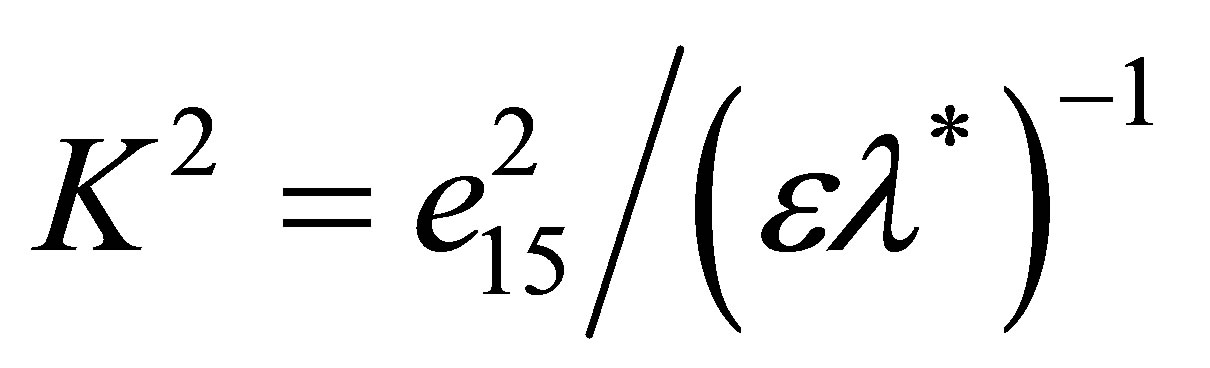
and
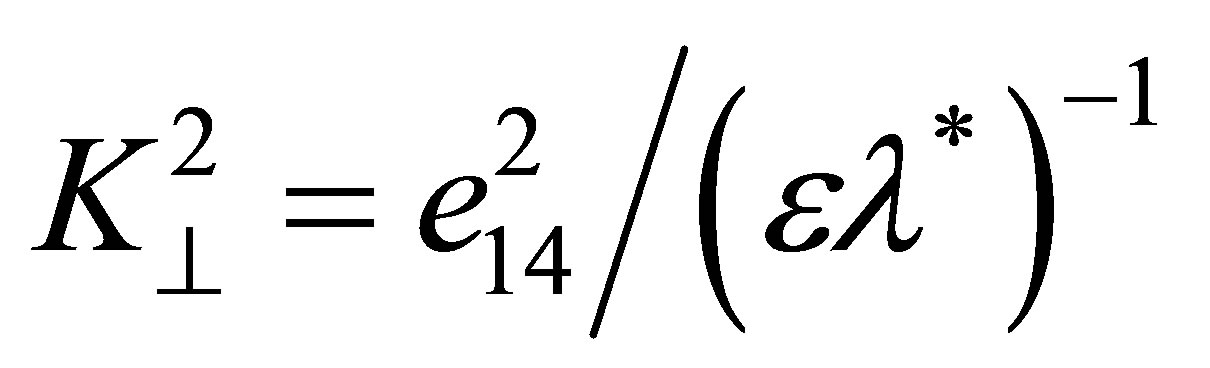
have sense of squares of the electromechanical coupling coefficients of piezoelectric with one only longitudinal or cross piezoactivity.
The procedure of addition before Bessel function and its derivative the above mentioned factor for transition from a boundary problem of a plane wave scattering to scattering of a cylindrical wave is in fact the basic result of work [9]. In our case this procedure, certainly, may be applied too to amplitude coefficients bn and cn of potentials of partial electrical oscillations in the expantions (6). It is enough to know only coefficients (11) for the analysis of wave scattering. Therefore we do not write out here appropriate expressions for bn and cn, as we do not research potentials of multipole oscillations (6).
According to asymptotic form of Hankel function [7] the radiation field of a linear source determined by the first sum (8), will be expressed in a case  by equality
by equality
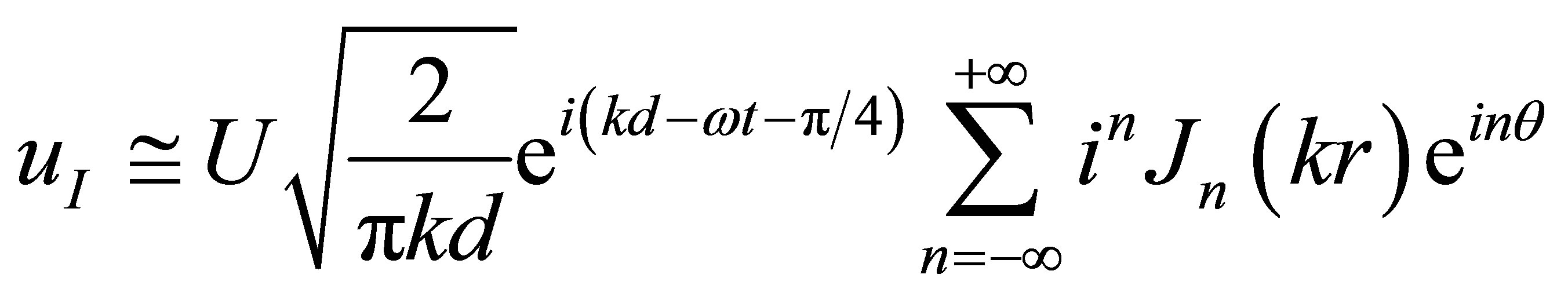 (13)
(13)
Infinite series in this formula converges to the exponent exp(ikx), where x = rcosq, and it is easy to conclude, that radiation field is the plane monochromatic shear wave propagating at the polar direction. The considered decision of a scattering problem of shear-axial cylindrical wave by a circular cavity in piezoelectric crystal, thus, turns into the decision of a scattering problem for wave with plane front [3]. It is necessary, however to remember, that as against [3] the amplitude of incident wave not remains constant. More adequately to consider the incident wave in asymptotic approximation 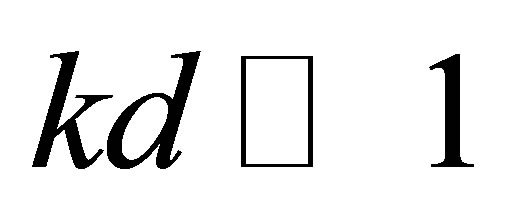 together with additional phase multiplier
together with additional phase multiplier
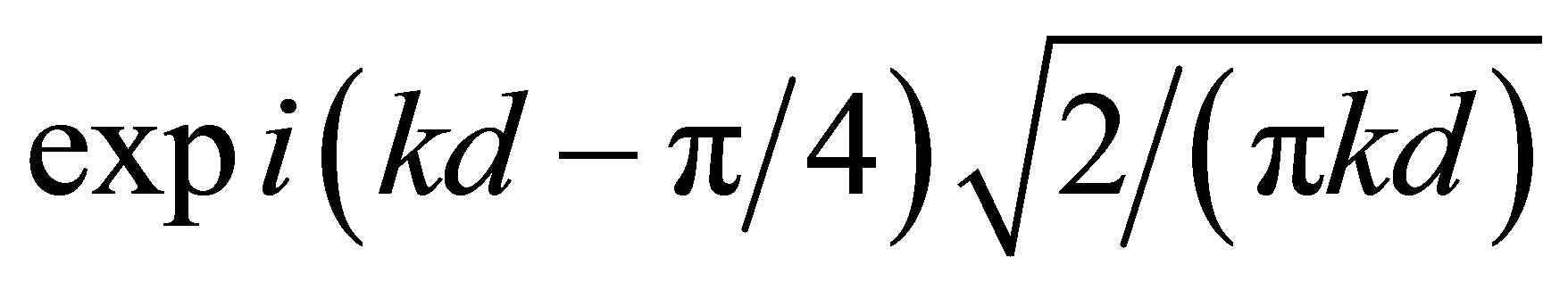 .
.
The given circumstance is necessary to take into account at comparison of results of the decisions (8), (9) in the area . This difference of asymptotic expressions of fields explains, in particular, disappearance of a shadow zone at scattering of a plane wave as an observation point is moving from an obstacle and, opposite, preservation of shadow zone at scattering cylindrical wave at any removals [8].
. This difference of asymptotic expressions of fields explains, in particular, disappearance of a shadow zone at scattering of a plane wave as an observation point is moving from an obstacle and, opposite, preservation of shadow zone at scattering cylindrical wave at any removals [8].
3. Integral Characteristics of a Cylindrical Wave Scattering
In order to judge about scattering over all set of partial waves use such integral characteristics, as amplitude characteristic of scattering FS(q) and total cross-section of scattering s(x). By definition (see, for example, [8]) FS represents complex amplitude of a scattering field in a far wave zone. Given value is interesting by one’s module, which characterizes azimuthal redistribution of scattering power. As opposite to it, the value s allows consider a frequency dependence of the part of radiated by a source, of total power that scatters by obstacle. In the certain sense FS is the efficiency characteristic of scattering estimated on angular (spatial) spectrum, and s is a spectral parameter of similar kind, but only in frequency representation. As dependences FS(q) and s(x) mutually supplements each other they must be analyzed together to give more complete picture of scattering.
For determination FS(q) may be used an asymptotic expression of scattering field (5), that is similar to (13) and follows from an asymptotic expression of function 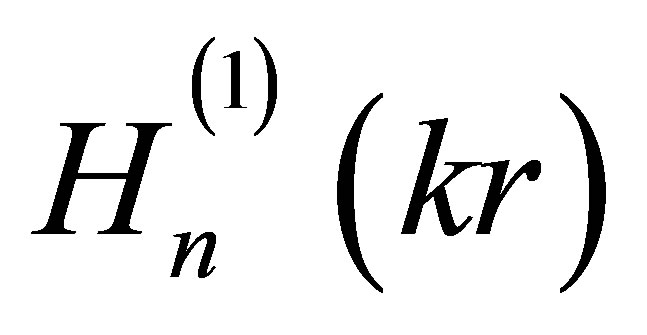 for
for :
:
 .
.
The appropriate substitution in formula (6) for the scattering field, gives
 . (14)
. (14)
Here multiplier before the sum of series presents the cylindrical wave uniformly divergent from a cavity on all directions. At the same time the series of convergent azimuthal harmonics is the factor that corrects the amplitude of this wave due to non-uniformity of its scattering on an azimuth and has usually name of the amplitude characteristic of scattering. Thus, the definition of value FS in case of a cylindrical wave scattering does not differ in form from its definition for scattering of a plane wave [1, 2]
 . (15)
. (15)
The actually having place the distinction between these cases of scattering will be shown only through difference of amplitude coefficients an in the formulas (10), (11).
For the total cross-section scattering s we have 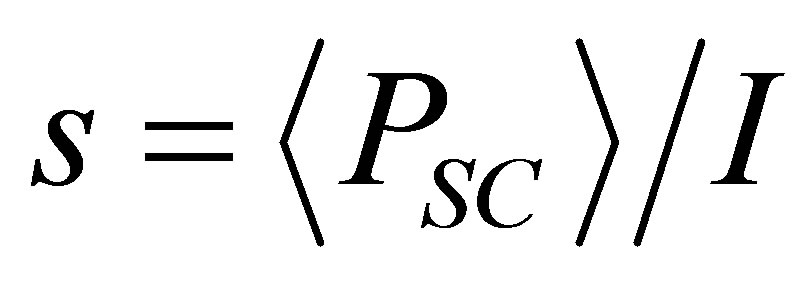 and if on the average the scattering power
and if on the average the scattering power 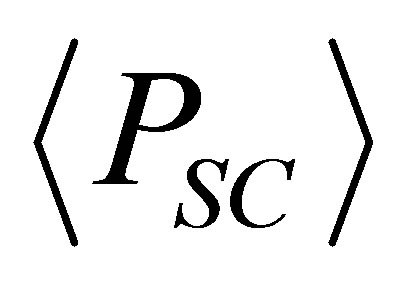 in view of independence of properties of a radiation source is like FS will not change the form:
in view of independence of properties of a radiation source is like FS will not change the form:
 the intensity of a radiation source I will change. For a plane wave it is equal [9,10] I = wl*kU2/2 that leads to classical result
the intensity of a radiation source I will change. For a plane wave it is equal [9,10] I = wl*kU2/2 that leads to classical result
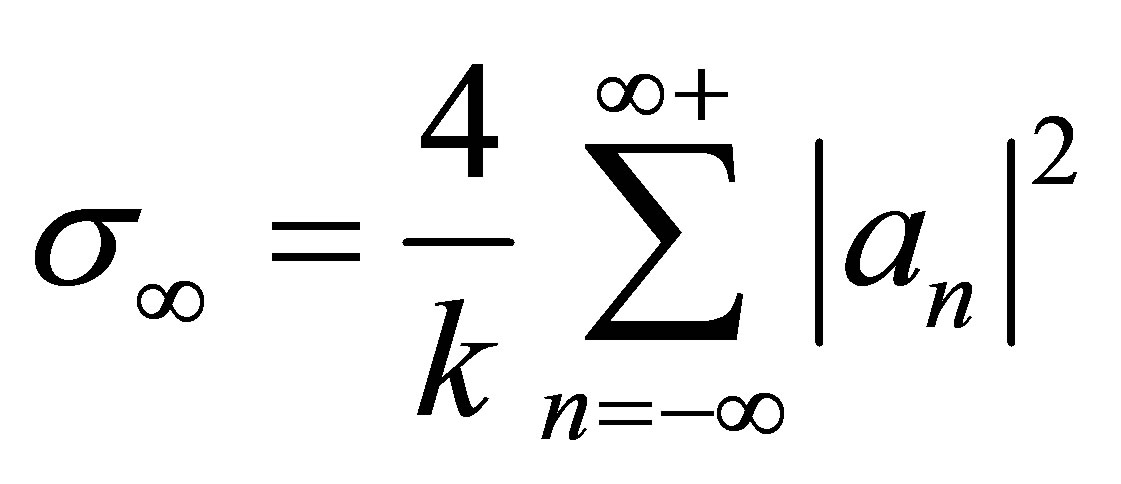 . (16)
. (16)
for the ultimate (at kd ® ¥) value of the cross section s of cylindrical wave scattering. Equation (16) was used in [3] at performance of numerical calculations of total cross-section scattering of a plane monochromatic wave by a cavity in a piezoelectric crystal.
For the shear-axial cylindrical wave the calculation of intensity can be executed, proceeding from representation of an average radial flow of energy in cylindrical coordinates of a source [11], following the formula
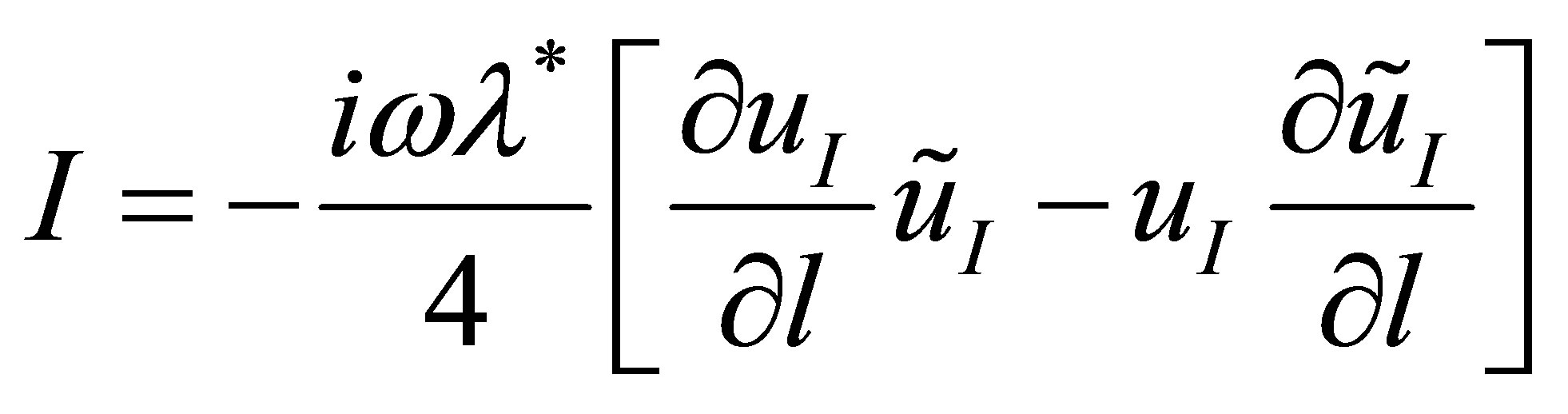 . (17)
. (17)
Here as radial coordinate the module of a vector l (see figure 1) is used, and tilde from above designates complex conjugation. According to the first formula (5), the value in square brackets of expression (17) to within multiplier kU2 forms Wronskian  of Hankel functions of the first and second kind of the zero order from argument x = kl [7]. By a result of the calculations we have
of Hankel functions of the first and second kind of the zero order from argument x = kl [7]. By a result of the calculations we have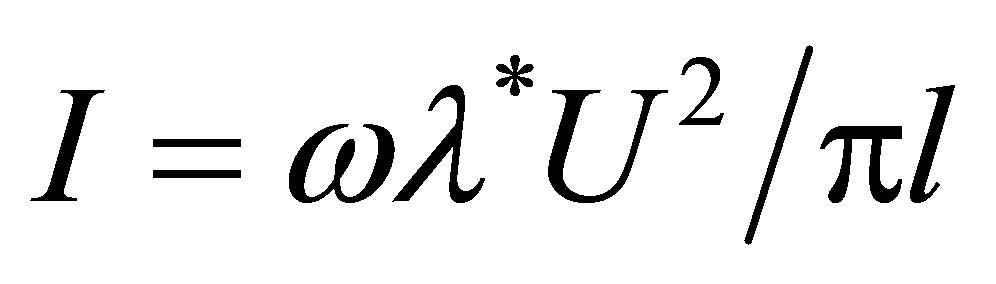 , that gives
, that gives
 . (18)
. (18)
It is visible, that because of divergence of a cylindrical wave front a section scattering on unit of length of a cavity any more will not be similar s¥ the constant value, and linearly depends on radial coordinate counted off source up to an observation point. The choice of observation point at calculation of intensity of a cylindrical wave uI it is natural to connect with a location of the scattering obstacle i.e. with centre of a cavity. In this connection in (18) at definition of total cross-section scattering of cylindrical wave by a cavity sS let us assume l = d, i.e. we shall accept
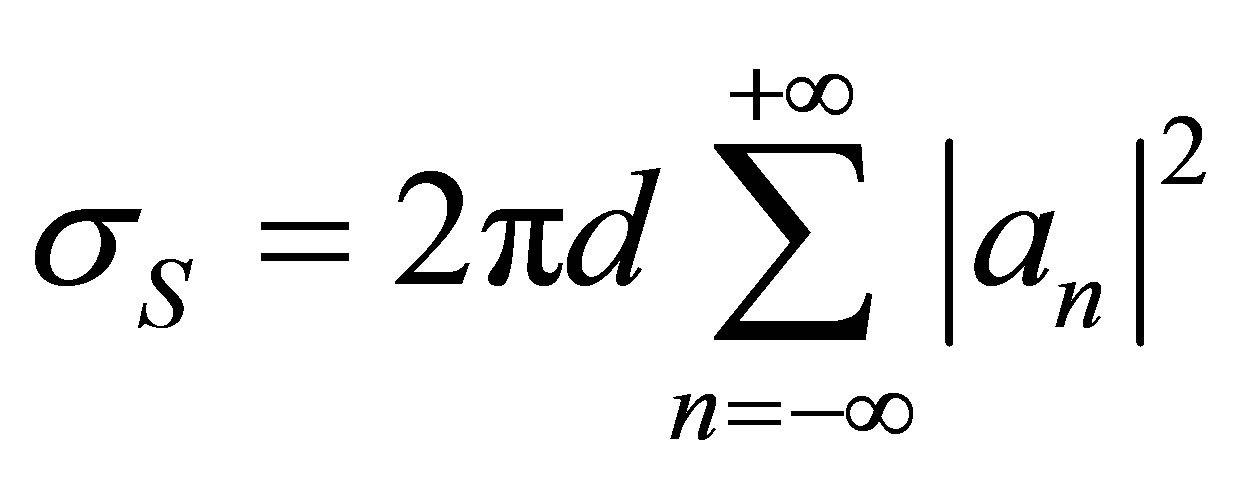 . (19)
. (19)
Similar renormalization of value s on spatial coordinate was used in work [12].
4. Discussion of the Results
The formulas (11), (15), (19) are used below for calculation of scattering indicatrix 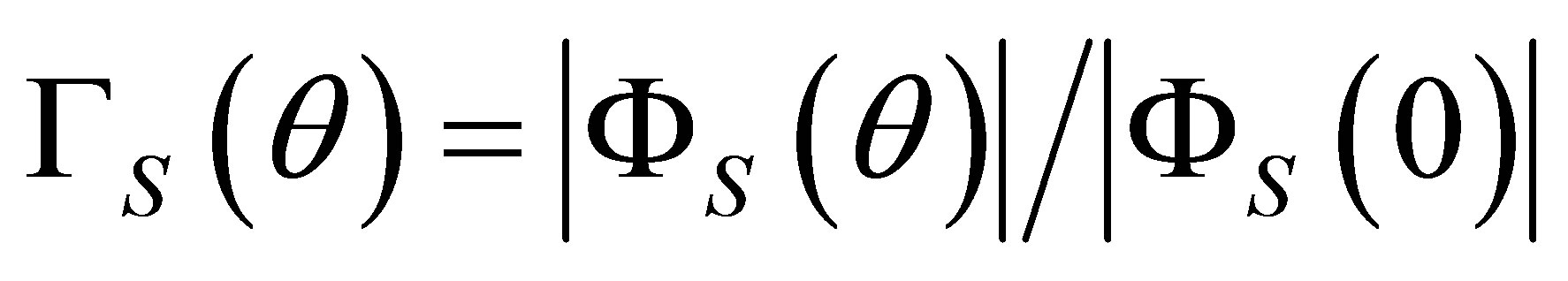 and section of scattering sS of a shear-axial wave by a circular air cavity with metallized (eC ® ¥) or not metallized (eC = e0, e0 is the permittivity of free space) surface in piezoelectric ceramics PZT-4 (K2 = 0.5,
and section of scattering sS of a shear-axial wave by a circular air cavity with metallized (eC ® ¥) or not metallized (eC = e0, e0 is the permittivity of free space) surface in piezoelectric ceramics PZT-4 (K2 = 0.5,  , e @ 730 e0). As varied parameter wave distance from a source up to an axis of a cavity kd > x was considered.
, e @ 730 e0). As varied parameter wave distance from a source up to an axis of a cavity kd > x was considered.
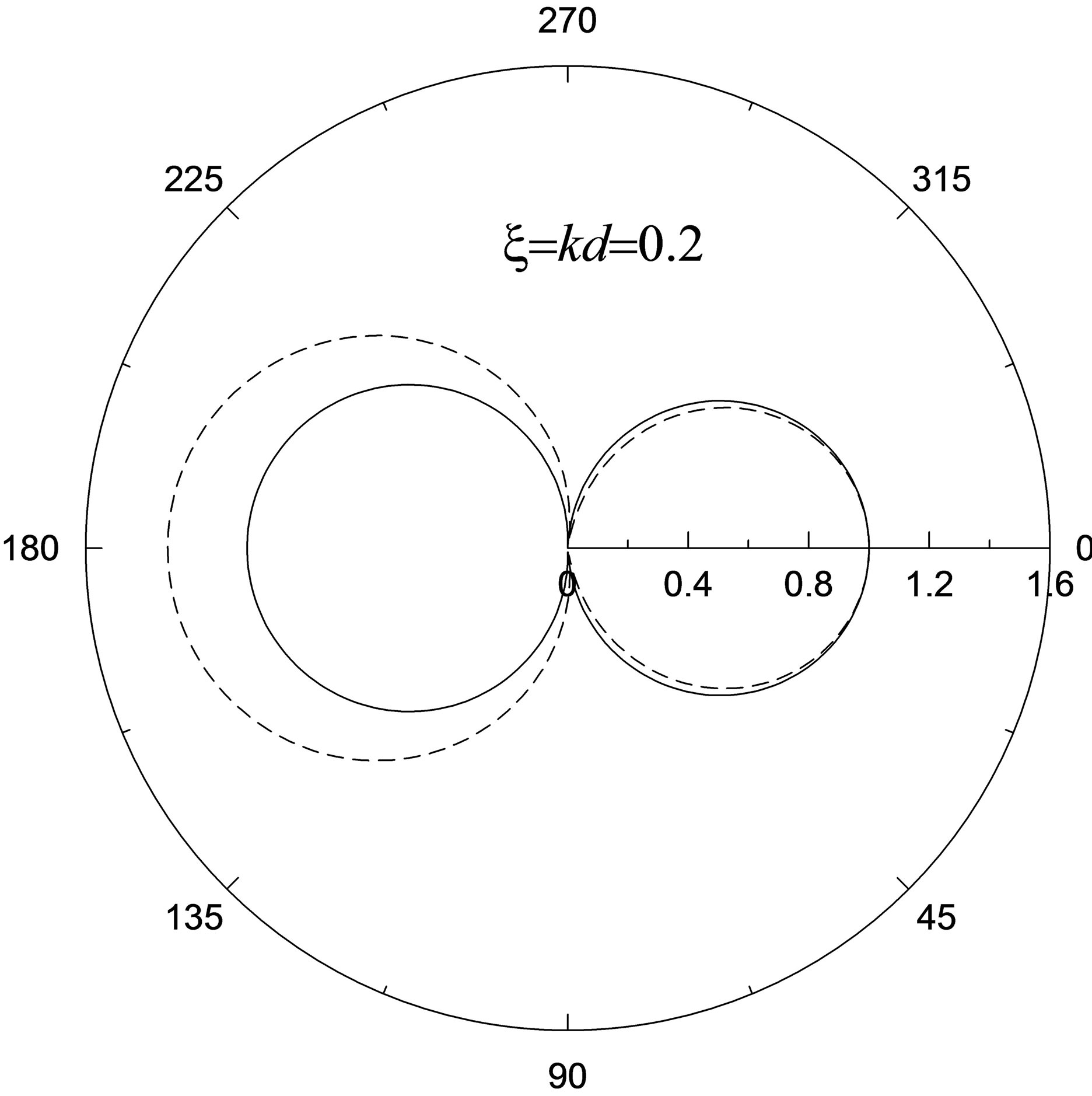
On low frequencies  scattering indicatrixes have the characteristic dipol form: the scattering a little or is absent in vertical azimuths (figures 2) q = p/2, 3p/2, and, on the contrary, is maximum in location direction q = 0 (shady lobe) or direction of back scattering: q = p. As a radiation source move off a cavity (kd changes from the minimal value x to infinity) scattering indicatrixes of a cylindrical wave (see continuous curves) change only in the direction of a back scattering, appreciably approaching to the scattering indicatrixes of a plane wave shown dashed lines. Thus, the curvature of front of a scattering wave in area of low frequencies practically has not an effect for formation of a shadow. For an explanation this should search that at the small wave sizes of a cavity of scattering waves with identical efficiency come into area of a shadow as in case of plane, and cylindrical wave.
scattering indicatrixes have the characteristic dipol form: the scattering a little or is absent in vertical azimuths (figures 2) q = p/2, 3p/2, and, on the contrary, is maximum in location direction q = 0 (shady lobe) or direction of back scattering: q = p. As a radiation source move off a cavity (kd changes from the minimal value x to infinity) scattering indicatrixes of a cylindrical wave (see continuous curves) change only in the direction of a back scattering, appreciably approaching to the scattering indicatrixes of a plane wave shown dashed lines. Thus, the curvature of front of a scattering wave in area of low frequencies practically has not an effect for formation of a shadow. For an explanation this should search that at the small wave sizes of a cavity of scattering waves with identical efficiency come into area of a shadow as in case of plane, and cylindrical wave.
Concerning back scattering here it is necessary to add, that at a close arrangement of a source to a cavity (kd @ x) it will be weaker not only back scattering of a plane wave (figure 2(a)), but also back scattering of the appropriate cylindrical wave at absence piezoelectric effect. The situation varies at kd > 1, when the back scattering becomes close to back scattering of a plane wave (figure 2(b)) and will exceed back scattering of a cylindrical wave of the same curvature by a cavity of the same wave size, but not in a piezoelectric material.
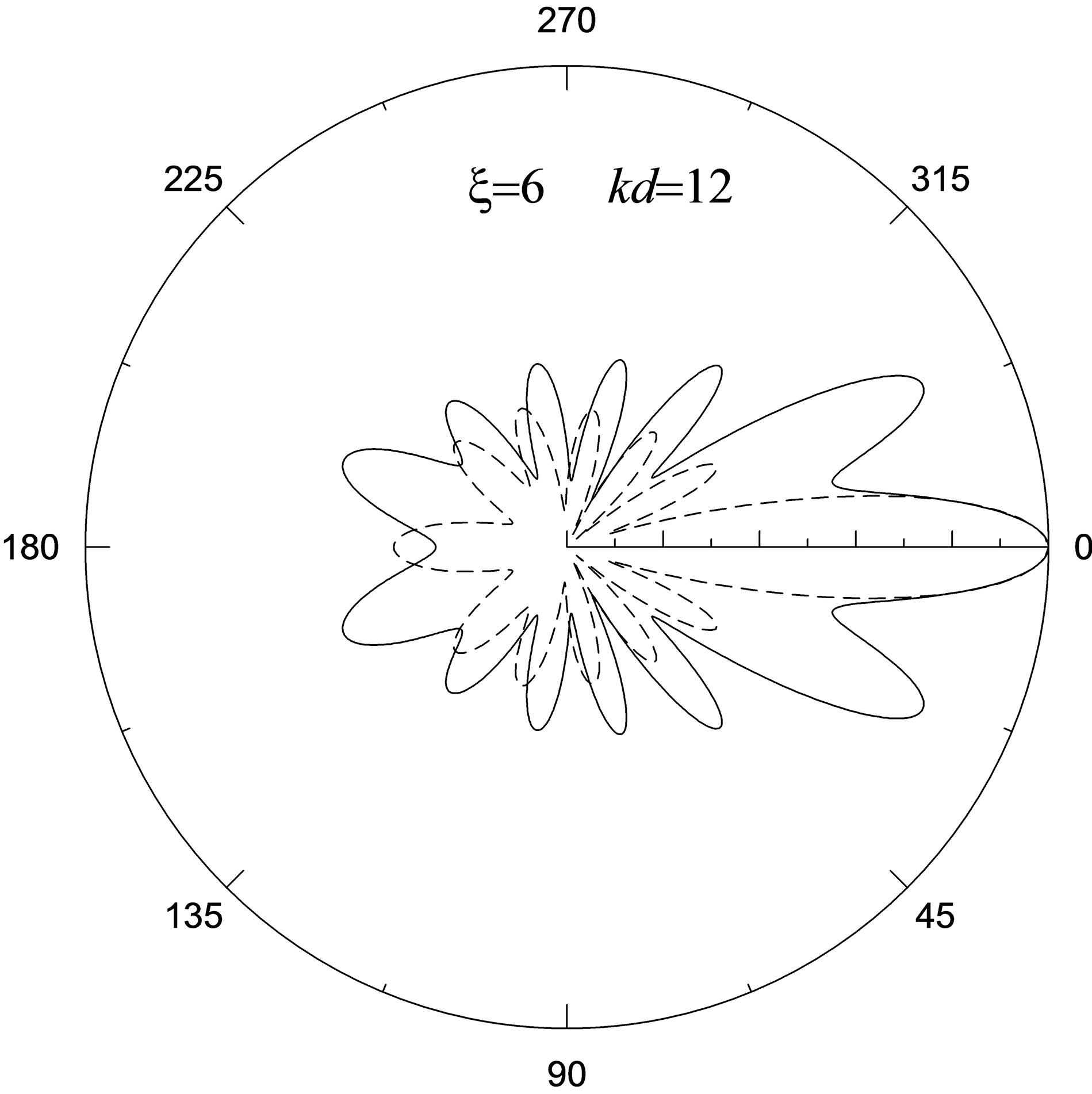
On moderate frequencies (1 < x < 10), as show a figures 3 and 4, as a radiation source is being removed off a cavity the form of scattering indicatrixex with growth x becomes complicated of the appearance of more and
 (a)
(a)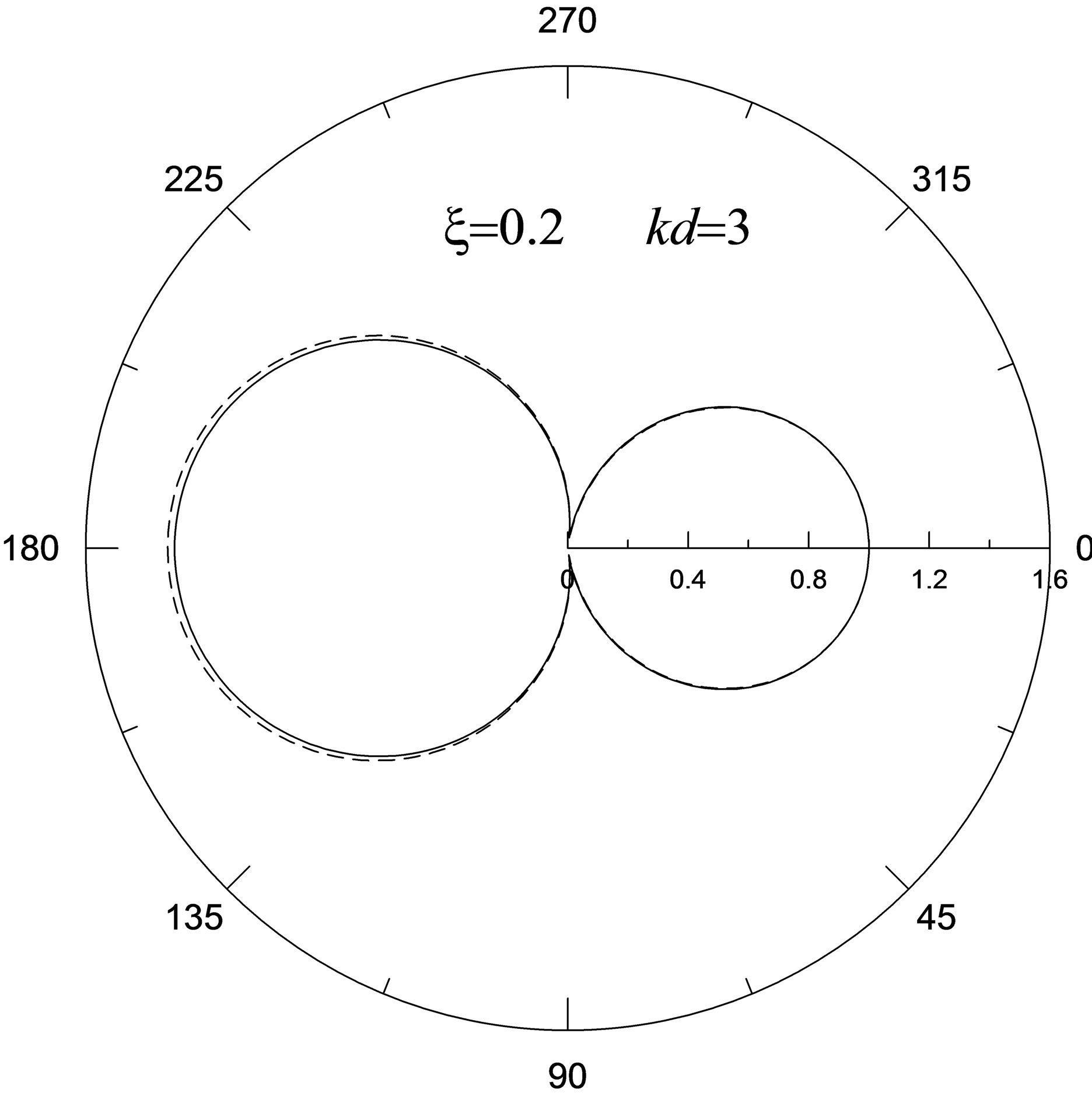 (b)
(b)
Figure 2. Low-frequency (x = 0.2) scattering indicatrixes for the cylindrical (continuous curves) and plane (dashed curves) shear-axial waves scattered by circular metallized cavity in piezoelectric ceramics PZT-4: a): kd = 0.2 ; b): kd = 3.
more great number of minor lobes and decrease of intensity I of a scattering wave. The greatest difference of scattering indicatrix of a cylindrical wave, that expressed by amplification of its scattering in comparison with a plane wave on all azimuths with the exception forward direction q = 0, take place at the small distances between a radiation source and cavity when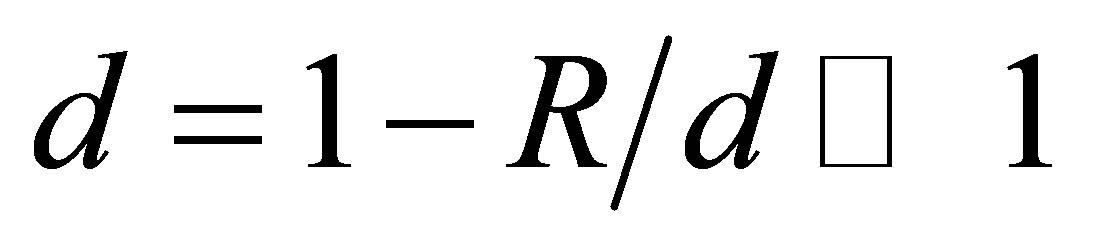 . The indicatrix in figure 3(b) corresponds to the least value d = 0.25 accepted in calculations, while for the greatest
. The indicatrix in figure 3(b) corresponds to the least value d = 0.25 accepted in calculations, while for the greatest
 (a)
(a)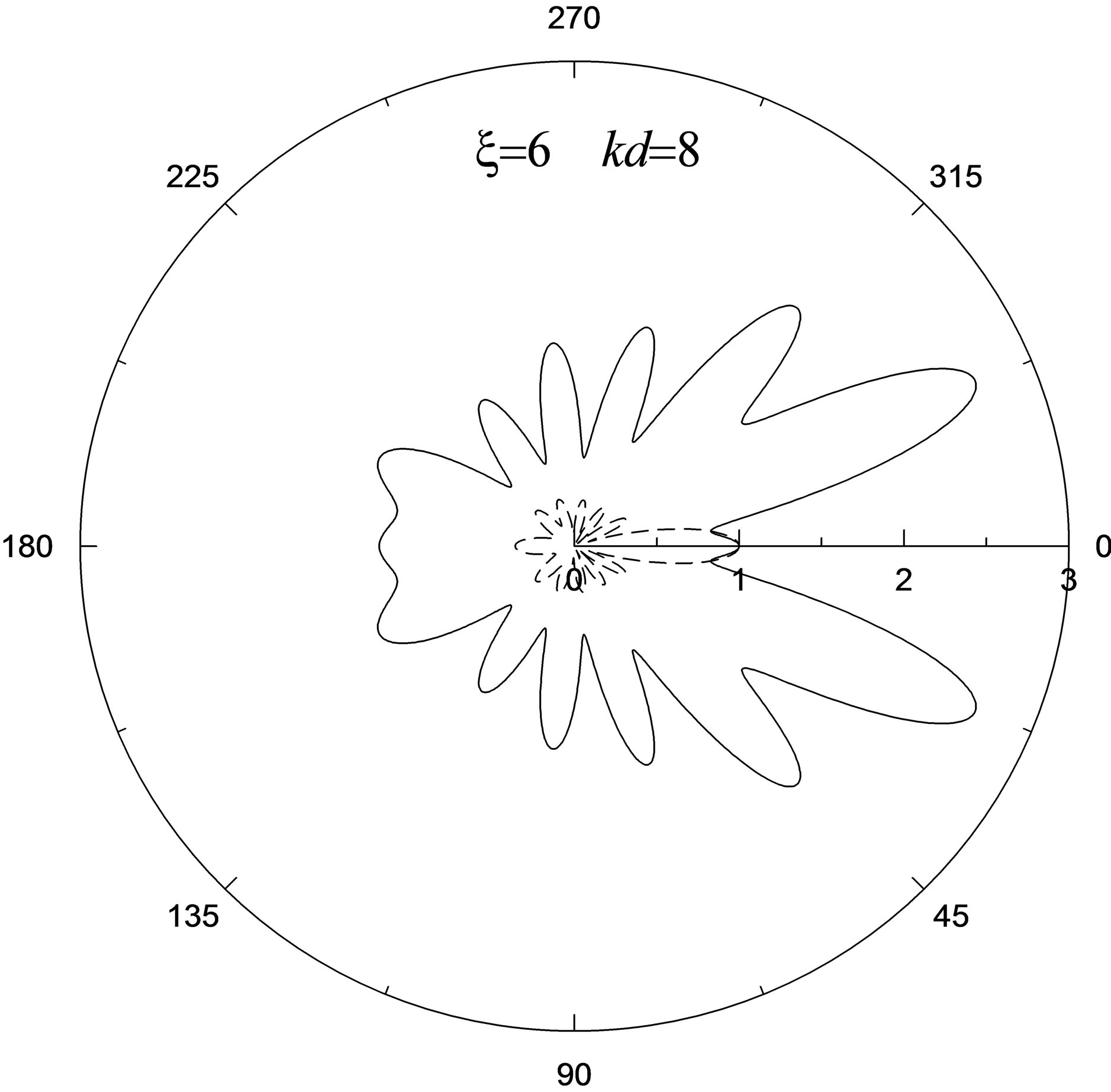 (b)
(b)
Figure 3. The indicatrixes of shear cylindrical (continuous curves) and plane (dashed curves) wave scattering by circular metallized cavity in piezoelectric ceramic PZT-4 on moderate frequencies: a) x = 3, kd = 5 ; b) x = 6, kd = 8.
value d = 0.8 the proper indicatrix is presented in figure 4(b). So in first case we have especially high distinctions of the indicatrixes for scattering of cylindrical and plane waves. On the contrary in second case the scattering indicatrix of the cylindrical wave approaches in the form to the scattering indicatrix of the plane wave having parameter d = 1.
In a figure 5 the spectra 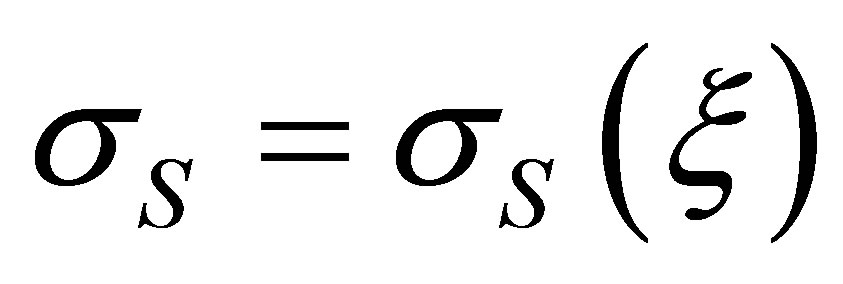 of total crosssection scattering of a cylindrical wave by a metallized
of total crosssection scattering of a cylindrical wave by a metallized
 (a)
(a) (b)
(b)
Figure 4. The indicatrixes of shear cylindrical (continuous curves) and plane (dashed curves) wave scattering by circular metallized cavity in piezoelectric ceramic PZT-4 on moderate and high frequencies: a) x = 6, kd = 12; b) x = 10, kd = 50.
cavity, which were normalized to geometric-optical value 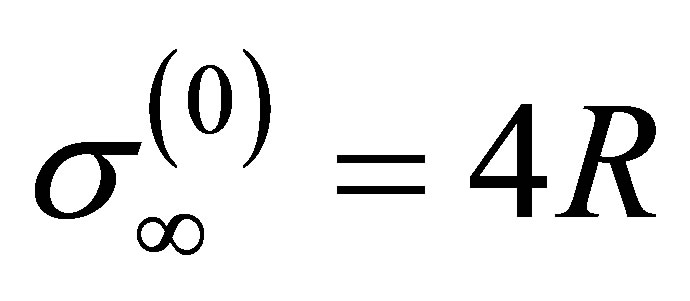 of cross-section scattering for a plane wave, are submitted. The horizontal dashed line here and in a figure 6, where the similar spectra were calculated for the case of nonmetallized cavity, corresponds to the geometric-optic limit. The spectral curve coming nearer and nearer to horizontal dashed line as kd ® ¥ and appropriate to a plane wave scattering, was calculated at the
of cross-section scattering for a plane wave, are submitted. The horizontal dashed line here and in a figure 6, where the similar spectra were calculated for the case of nonmetallized cavity, corresponds to the geometric-optic limit. The spectral curve coming nearer and nearer to horizontal dashed line as kd ® ¥ and appropriate to a plane wave scattering, was calculated at the

Figure 5. The spectra of total cross-section scattering of a cylindrical shear-axial wave by the metallized cavity in piezoelectric ceramic PZT-4 at the values: kd = 10, 15, 40 and 70.

Figure 6. The spectra of total cross-section scattering of a cylindrical shear-axial wave by the nonmetallized cavity in piezoelectric ceramic PZT-4 at the values: kd = 10, 15, 40 and 70.
large values kd @ 300. As against it all other spectra of total cross-section scattering have due to the finiteness of variable parameter kd = 10, 15, 40 and 70 the top boundary xmax = kd resulting from obvious geometrical restriction (see figure 1) d ³ R.
Distinctive feature of spectra of a figure 5 is the small-scale oscillations of total cross-section scattering caused by piezoelectric effect. Their nature was explicated in [3] for a case of a plane wave scattering and connected with a possibility of existence on metallized boundary of a cavity of well-localized circulating electroacoustic waves. It is visible, that on the top boundary of a spectrum the curves of dependences 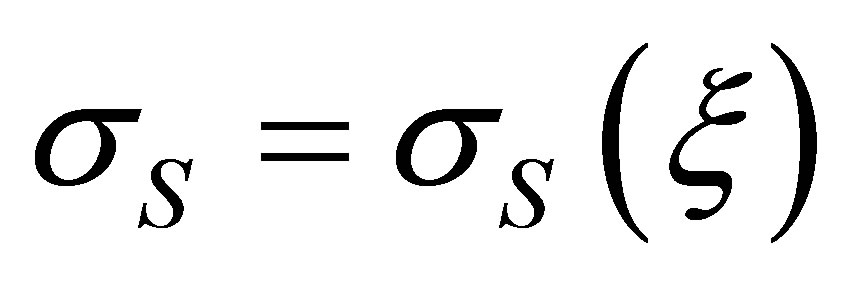 because of growth of shielding action of a cavity on a radiation source undergo essential rise. Here the amplitudes of spectral oscillations (kd @ 70, kd ® ¥) sharply grow too. Indirectly it testifies effective excitation of a circulating electroacoustic wave by near-located linear source on boundary of the large wave size cavity.
because of growth of shielding action of a cavity on a radiation source undergo essential rise. Here the amplitudes of spectral oscillations (kd @ 70, kd ® ¥) sharply grow too. Indirectly it testifies effective excitation of a circulating electroacoustic wave by near-located linear source on boundary of the large wave size cavity.
Submitted on a figure 6 for comparison the spectra of total cross-section scattering of a cylindrical wave by nonmetallized cavity have no appreciable small-scale oscillations, as in the case value  reduces almost on three orders. The spectra
reduces almost on three orders. The spectra 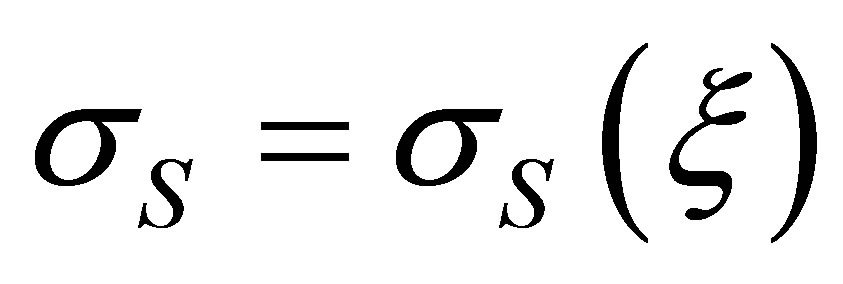 therefore do not differ from spectra of total cross-section scattering of a cylindrical shear-axial wave by a cavity in usual elastic medium. However, they also have the top boundaries, near to which undergo some rise above the geometricoptic level.
therefore do not differ from spectra of total cross-section scattering of a cylindrical shear-axial wave by a cavity in usual elastic medium. However, they also have the top boundaries, near to which undergo some rise above the geometricoptic level.
5. Conclusion
In the paper the distinctive features of a cylindrical shear wave scattering by a circular cavity of a piezoelectric crystal are considered in comparison with the scattering of a plane shear wave. It is shown that they are essential to a location of a radiation source of a shear wave near to a cavity surface and disappear in the process of its removal off a cavity on distances and in large scale wave length. The top boundary of scattering spectrum, specific to cylindrical waves, is established, and near to the waves, essential oscillations of total cross-section scattering take place due to piezoelectric effect in a case of a metallized cavity in high frequencies.
REFERENCES
- N. S. Shevyakhov, “Scattering of a Shear Wave from a Low-Ohmic Cylinder Cavity in a Piezoelectric of Class C6V (C4V),” Soviet Physical Acoustics, Vol. 24, No. 2, 1978, pp. 150-153.
- N. S. Shevyakhov, “Some Features of Transverse Wave Scattering on Cylindrical Cavity with Semiconductor in Hexagonal Piezoelectric,” Akusticheskij Zhurnal, Vol. 31, No. 3, 1985, pp. 380-384.
- N. S. Shevyakhov, “Total Scattering Cross-Section of a Shear Wave Scattered from a Cavity in a Hexagonal or Tetragonal Piezoelectric,” Acoustical Physics, Vol. 44, No. 6, 1998, pp. 747-749.
- N. S. Shevyakhov, “On Electrodynamic Addition to the Total Cross Section of Shear Wave Scattering by Cylindrical Cavity in a Piezoelectric Material,” Fisika Volnovykh Protsessov i Radiotekhnicheskie Sistemy, Vol. 2, No. 1, 1999, pp. 15-19.
- V. D. Natsik and K. A. Chishko, “Sound Radiation during Annihilation of Dislocations,” Fisika Tverdogo Tela, Vol. 14, No. 11, 1972, pp. 3126-3132.
- V. S. Boiko, R. I. Garber, V. F. Kivshik and L. F. Krivenko, “Experimental Investigation of the Transition Sound Radiation Emitted by Dislocations Emerging to the Surface,” Soviet Physics JETP, Vol. 44, No. 2, 1976, pp. 372-375.
- G. N. Watson, “A Treatise on the Theory of Bessel Functions,” Cambridge University Press, London, 1922.
- E. L. Shenderov, “Radiation and Scattering of Sound,” Sudostroenie, Leningrad, 1989.
- T. J. Cavicci and W. D. O’Brien, “Acoustic Scattering of an Incident Cylindrical Wave by an Infinite Circular Cylinder,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Contral, Vol. 35, No. 1, 1988, pp. 78-80. http://dx.doi.org/10.1109/58.4152
- R. Truell, Ch. Elbaum and B. Chick, “Ultrasonic Methods in Solid State Physics,” Academic, New York, 1969.
- M. K. Balakirev and I. A. Gilinskii, “Waves in piezo-crystals,” Nauka, Novosibirsk, 1982.
- S. Arslanagic, R. W. Ziolkowski and O. Breinbjerg, “Exitation of an Electrically Small Metamaterial-Coated Cylinder by an Arbitrary Located Line Source,” Microwave and Optical Technology Letters, Vol. 48, No. 12, 2006, pp. 2598-2606. http://dx.doi.org/10.1002/mop.21990

