Open Journal of Discrete Mathematics
Vol.2 No.3(2012), Article ID:21140,5 pages DOI:10.4236/ojdm.2012.23016
Hamiltonian Cayley Digraphs on Direct Products of Dihedral Groups*
Department of Mathematics and Statistics, University of Winnipeg, Winnipeg, Canada
Email: chuker31@hotmail.com, s.gosselin@uwinnipeg.ca, easyzeng@gmail.com
Received May 9, 2012; revised June 10, 2012; accepted June 26, 2012
Keywords: Hamilton Cycle; Cayley Digraph; Dihedral Group
ABSTRACT
We prove that a Cayley digraph on the direct product of dihedral groups D2n × D2m with outdegree two is Hamiltonian if and only if it is connected.
1. Introduction
1.1. Definitions
For a finite group G and a subset S of G, the Cayley digraph  is the directed graph with vertex set G and arcs from
is the directed graph with vertex set G and arcs from  to
to  for each
for each  and
and . The set S is often called the connection set of the digraph
. The set S is often called the connection set of the digraph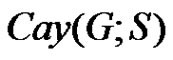 , and this digraph is connected if and only if
, and this digraph is connected if and only if 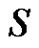 is a generating set for G. The connection set S is said to be minimal if it is a minimal generating set of G, and it is said to be minimum if it is a minimal connection set of minimum cardinality. A Hamilton cycle (path) in a digraph of with n vertices is a directed cycle (path) with n vertices. A digraph is said to be Hamiltonian if it has a Hamilton cycle.
is a generating set for G. The connection set S is said to be minimal if it is a minimal generating set of G, and it is said to be minimum if it is a minimal connection set of minimum cardinality. A Hamilton cycle (path) in a digraph of with n vertices is a directed cycle (path) with n vertices. A digraph is said to be Hamiltonian if it has a Hamilton cycle.
Each arc in  of the form
of the form  is labelled
is labelled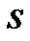 , and called an s-arc. A Hamilton cycle in
, and called an s-arc. A Hamilton cycle in 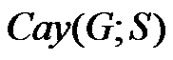 can be specified by the sequence of vertices encountered or by the sequence of arcs traversed. In the latter case, it is often more convenient to list the labels of the arcs, rather than the arcs themselves, since for each vertex there is exactly one out-arc with label
can be specified by the sequence of vertices encountered or by the sequence of arcs traversed. In the latter case, it is often more convenient to list the labels of the arcs, rather than the arcs themselves, since for each vertex there is exactly one out-arc with label  for each
for each . An ordered sequence
. An ordered sequence  of the arc labels encountered in a Hamilton cycle is called a Hamiltonian arc sequence. Since Cayley digraphs are vertextransitive, any cyclic shift of a Hamiltonian arc sequence of a Cayley digraph is also a Hamiltonian arc sequence of the digraph, and traversing a Hamiltonian arc sequence of a Cayley digraph starting from any vertex will yield a Hamilton cycle of the digraph. For convenience and brevity, we sometimes omit the commas and brackets from an arc sequence. For an arc sequence x, the symbol
of the arc labels encountered in a Hamilton cycle is called a Hamiltonian arc sequence. Since Cayley digraphs are vertextransitive, any cyclic shift of a Hamiltonian arc sequence of a Cayley digraph is also a Hamiltonian arc sequence of the digraph, and traversing a Hamiltonian arc sequence of a Cayley digraph starting from any vertex will yield a Hamilton cycle of the digraph. For convenience and brevity, we sometimes omit the commas and brackets from an arc sequence. For an arc sequence x, the symbol 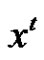 denotes the concatenation of
denotes the concatenation of  copies of
copies of . If
. If  for some
for some  and
and , we sometimes write
, we sometimes write

to denote the fact that there is an s-arc from 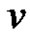 to
to  in
in .
.
For an integer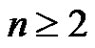 , the symbol
, the symbol  denotes the dihedral group of order
denotes the dihedral group of order . For
. For  this is the group of symmetries of the regular
this is the group of symmetries of the regular  -gon under the operation of function composition, and it has the presentation
-gon under the operation of function composition, and it has the presentation , where R is the counterclockwise rotation of
, where R is the counterclockwise rotation of  and
and  is a reflection across any axis of symmetry. For n = 2 the same presentation can be used to define D4. Note that
is a reflection across any axis of symmetry. For n = 2 the same presentation can be used to define D4. Note that .
.
1.2. History and Layout of the Paper
One fundamental problem is that of determining which Cayley digraphs are Hamiltonian. This is a longstanding problem which can be traced back to bell ringing, or campanology, since the orders in which a set of church bells may be rung form a group, and a Hamilton cycle in a Cayley digraph of this group gives a sequence of these bell ringing orders which is pleasing to the ear. The problem is longstanding mainly due to its difficulty. There are several good surveys on the problem, including [1-3], which discusses recent progress and current directions in the more general related problem of finding Hamilton cycles and paths in vertex-transitive graphs.
One of the first elegant results on the problem of the Hamiltonicity of Cayley digraphs is due to Rankin [4], who determined which connected Cayley digraphs on a group  with connection set
with connection set 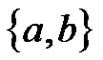 are Hamiltonian, in the case where
are Hamiltonian, in the case where  is a normal subgroup of
is a normal subgroup of .This solves the problem for Cayley digraphs with two generators for a class of groups which includes the Abelian groups, and some Cayley digraphs on solvable groups with two generators. In Section 2 we prove the following theorem.
.This solves the problem for Cayley digraphs with two generators for a class of groups which includes the Abelian groups, and some Cayley digraphs on solvable groups with two generators. In Section 2 we prove the following theorem.
Theorem 1.1. A Cayley digraph on  with outdegree two is Hamiltonian if and only if it is connected.
with outdegree two is Hamiltonian if and only if it is connected.
This is a new result since such digraphs do not satisfy the hypothesis of Rankin’s result. We first prove that if  is generated by two elements then both
is generated by two elements then both  and m are odd, and the proof makes use of the following result due to Gaschütz in 1955 [5].
and m are odd, and the proof makes use of the following result due to Gaschütz in 1955 [5].
Proposition 1.2. (Gaschütz [5]) Let  and
and  be groups. If
be groups. If  is finite, then
is finite, then  is generated by two elements if and only if each of the groups
is generated by two elements if and only if each of the groups  is generated by two elements, where
is generated by two elements, where 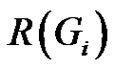 is the intersection of the maximal proper normal subgroups of
is the intersection of the maximal proper normal subgroups of  for
for .
.
2. Direct Products of Dihedral Groups
In this section we prove Theorem 1.1. We make use of the following lemma.
Lemma 2.1. If  is generated by two elements, then both
is generated by two elements, then both 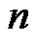 and
and  are odd.
are odd.
Proof: Since any dihedral group is generated by two elements, Proposition 1.2 implies that  is generated by two elements if and only if
is generated by two elements if and only if  is generated by two elements, where
is generated by two elements, where  and
and  denote the intersections of the maximal normal subgroups of
denote the intersections of the maximal normal subgroups of  and
and , respectively. If
, respectively. If  is even and
is even and , then the normal subgroups of
, then the normal subgroups of
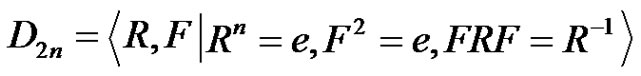
are
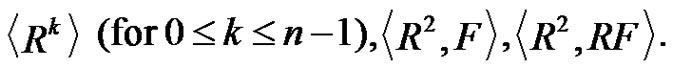
Thus the intersection of the maximal normal subgroups of  is
is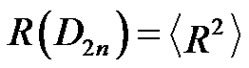 . On the other hand, if
. On the other hand, if  is odd, then the normal subgroups of
is odd, then the normal subgroups of  are all of the form
are all of the form  for
for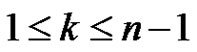 , and so in this case there is only one maximal normal subgroup, namely
, and so in this case there is only one maximal normal subgroup, namely . Note that
. Note that  and
and  . Thus Proposition 1.2 implies that if
. Thus Proposition 1.2 implies that if  and
and  are both even then
are both even then 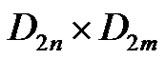 is generated by two elements if and only if
is generated by two elements if and only if  is generated by two elements, and if exactly one of n or m is even, say n is even, then
is generated by two elements, and if exactly one of n or m is even, say n is even, then  is generated by two elements if and only if
is generated by two elements if and only if 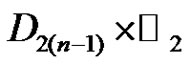 is generated by two elements. Using induction and the fact that
is generated by two elements. Using induction and the fact that , we conclude that if
, we conclude that if  or
or  is even and
is even and 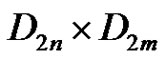 is generated by two elements, then either
is generated by two elements, then either  or
or  is generated by two elements, a contradiction. Hence both
is generated by two elements, a contradiction. Hence both 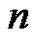 and
and  must be odd.
must be odd.
Proof of Theorem 1.1: If a Cayley digraph is Hamiltonian, then it is certainly connected. Conversely, if a Cayley digraph on  of outdegree two is connected, then
of outdegree two is connected, then  is generated by two elements. Let
is generated by two elements. Let 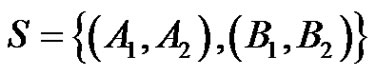 be a generating set for
be a generating set for . By Lemma 2.1, both
. By Lemma 2.1, both  and
and  must be odd. If
must be odd. If  and
and  are both rotations in
are both rotations in  for some
for some , then S does not generate
, then S does not generate , a contradiction. Hence at least one of
, a contradiction. Hence at least one of  and
and  is a reflection for
is a reflection for . If
. If 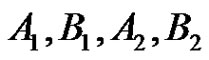 are all reflections, then every element in
are all reflections, then every element in  is an ordered pair of reflections or an ordered pair of rotations, a contradiction. If a rotation in
is an ordered pair of reflections or an ordered pair of rotations, a contradiction. If a rotation in  does not generate the cyclic subgroup of rotations of
does not generate the cyclic subgroup of rotations of , or if a rotation in
, or if a rotation in  does not generate the cyclic subgroup of rotations of
does not generate the cyclic subgroup of rotations of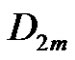 , then S does not generate all of
, then S does not generate all of , a contradiction. Thus any 2-element generating set
, a contradiction. Thus any 2-element generating set  must have one of the following two forms:
must have one of the following two forms:
1)  for reflections
for reflections  and
and , and rotations
, and rotations  and
and  or orders
or orders 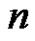 and
and , respectively.
, respectively.
We will show that
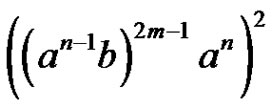
is a Hamiltonian arc sequence in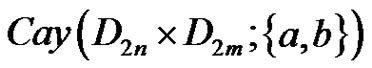 . Each element of
. Each element of  may be written uniquely in the form
may be written uniquely in the form  where
where ,
,  , and
, and . For convenience, we will represent the element
. For convenience, we will represent the element  by the ordered string
by the ordered string . Following the arc labelled
. Following the arc labelled  from a given vertex
from a given vertex  of the digraph increases the value of
of the digraph increases the value of  by 1 modulo
by 1 modulo  if
if , decreases the value of
, decreases the value of  by 1 modulo
by 1 modulo 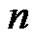 if
if , fixes the value of
, fixes the value of , increases the value of
, increases the value of 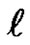 by 1 modulo 2, and fixes the value of
by 1 modulo 2, and fixes the value of . Similarly, following the arc labelled
. Similarly, following the arc labelled  from a given vertex
from a given vertex 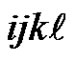 of the digraph increases the value of
of the digraph increases the value of  by 1 modulo
by 1 modulo 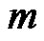 if
if , decreases the value of
, decreases the value of  by 1 modulo
by 1 modulo  if
if , fixes the value of
, fixes the value of , increases the value of
, increases the value of  by 1 modulo 2, and fixes the value of
by 1 modulo 2, and fixes the value of .
.
Starting for the identity vertex 0000 and following the sequence , we form a path which visits each vertex of the form
, we form a path which visits each vertex of the form , for which
, for which  and
and  have the same parity, exactly once. Now following
have the same parity, exactly once. Now following  we extend this path to visit each vertex of the form
we extend this path to visit each vertex of the form  where
where . Again following
. Again following , we visit each vertex of the form
, we visit each vertex of the form  where
where . Continuing in this way, starting from 0000 and following the arc sequence
. Continuing in this way, starting from 0000 and following the arc sequence , we form a path which visits each vertex of the form
, we form a path which visits each vertex of the form 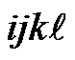 where both
where both  and
and . Starting from the last vertex on this path and following the arc sequence
. Starting from the last vertex on this path and following the arc sequence , we visit each vertex of the form
, we visit each vertex of the form 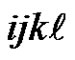 where
where  and
and . In total, starting from the identity vertex 0000 and following arc sequence
. In total, starting from the identity vertex 0000 and following arc sequence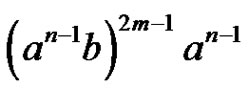 , we form a path which visits each vertex of the form
, we form a path which visits each vertex of the form  exactly once, where
exactly once, where . Now following arc
. Now following arc  from the last vertex on this path, we land on the first vertex
from the last vertex on this path, we land on the first vertex  of our path of the form
of our path of the form  with
with . Now repeating the arc sequence
. Now repeating the arc sequence , we visit each vertex of the form
, we visit each vertex of the form 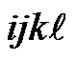 with
with  exactly once, and finish on the vertex
exactly once, and finish on the vertex . Thus we have formed a Hamilton path. Finally, following arc
. Thus we have formed a Hamilton path. Finally, following arc , we land back on the identity vertex 0000. Hence the complete arc sequence
, we land back on the identity vertex 0000. Hence the complete arc sequence is a Hamiltonian arc sequence. This arc sequence is shown in Figure 1 for the case where
is a Hamiltonian arc sequence. This arc sequence is shown in Figure 1 for the case where  and
and .
. 
2)  for reflections
for reflections  and
and , and rotations
, and rotations  and
and  or orders
or orders 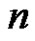 and
and , respectively.
, respectively.
In this case, we show that

is a Hamiltonian arc sequence in . First we will prove that this arc sequence traces out a walk in
. First we will prove that this arc sequence traces out a walk in  which visits all vertices, then we will show that this walk is closed. Note that each vertex of this graph can be written uniquely in the form
which visits all vertices, then we will show that this walk is closed. Note that each vertex of this graph can be written uniquely in the form  where
where ,
,  and
and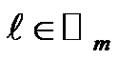 .
.
To see that the arc sequence  visits all vertices of the digraph, notice that starting at any vertex
visits all vertices of the digraph, notice that starting at any vertex  and following arc sequence
and following arc sequence , we visit all vertices in the coset of
, we visit all vertices in the coset of 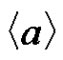 which contains
which contains . Hence, starting from
. Hence, starting from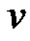 , if the vertex
, if the vertex 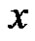 reached by arc sequence
reached by arc sequence 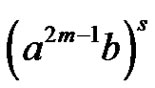 and the vertex
and the vertex  reached by arc sequence
reached by arc sequence  lie in different cosets of
lie in different cosets of  whenever
whenever , we can conclude that the arc sequence
, we can conclude that the arc sequence  traces out a walk which visits all vertices of the digraph. Suppose, for the sake of contradiction, that
traces out a walk which visits all vertices of the digraph. Suppose, for the sake of contradiction, that  and
and  lie in the same coset of
lie in the same coset of . We have
. We have
• 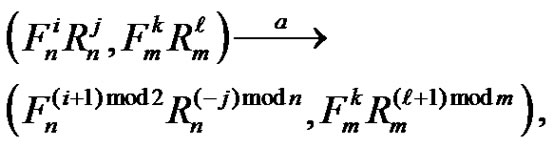
• 
• 
It is easy to see that traveling by a sequence of  -arcs doesn’t change the exponent of
-arcs doesn’t change the exponent of . Also, each time a vertex travels by an a-arc, its first coordinate alternates between
. Also, each time a vertex travels by an a-arc, its first coordinate alternates between  and
and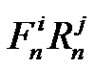 , and each time a vertex travels by the arc sequence
, and each time a vertex travels by the arc sequence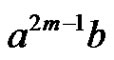 , its second coordinate alternates between
, its second coordinate alternates between  and
and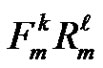 . Hence
. Hence
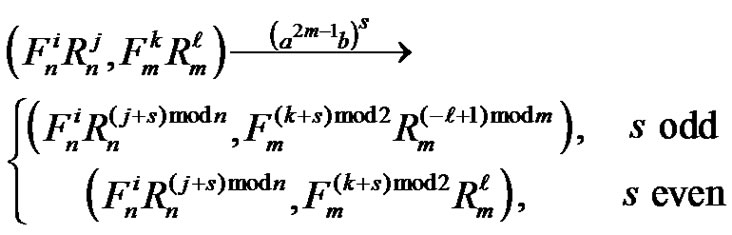
and
 .
.
Since  and
and  are in the same coset of
are in the same coset of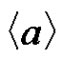 ,
,  can be reached from
can be reached from  through a sequence of
through a sequence of  -arcs, which does not change the exponent of
-arcs, which does not change the exponent of  in the second coordinate. Thus
in the second coordinate. Thus
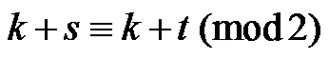
and so
 (1)
(1)
Also, since the exponent of  in
in  and
and  are equal,
are equal,  can be reached from
can be reached from  by a sequence of aarcs of even length. This implies that
by a sequence of aarcs of even length. This implies that
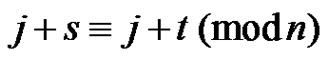
and thus

Since , this implies
, this implies , so
, so

But then since  is odd we have
is odd we have

which contradicts (1). We conclude that  and
and  lie in different cosets of
lie in different cosets of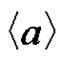 , and so the walk traced by the arc sequence
, and so the walk traced by the arc sequence  visits every vertex of the digraph.
visits every vertex of the digraph.
To show the walk is closed, we choose an initial vertex  and observe that
and observe that

Figure 1. Hamilton cycle in the Cayley digraph on D10 × D6 with connection set . The label
. The label 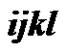 denotes the vertex
denotes the vertex .
.
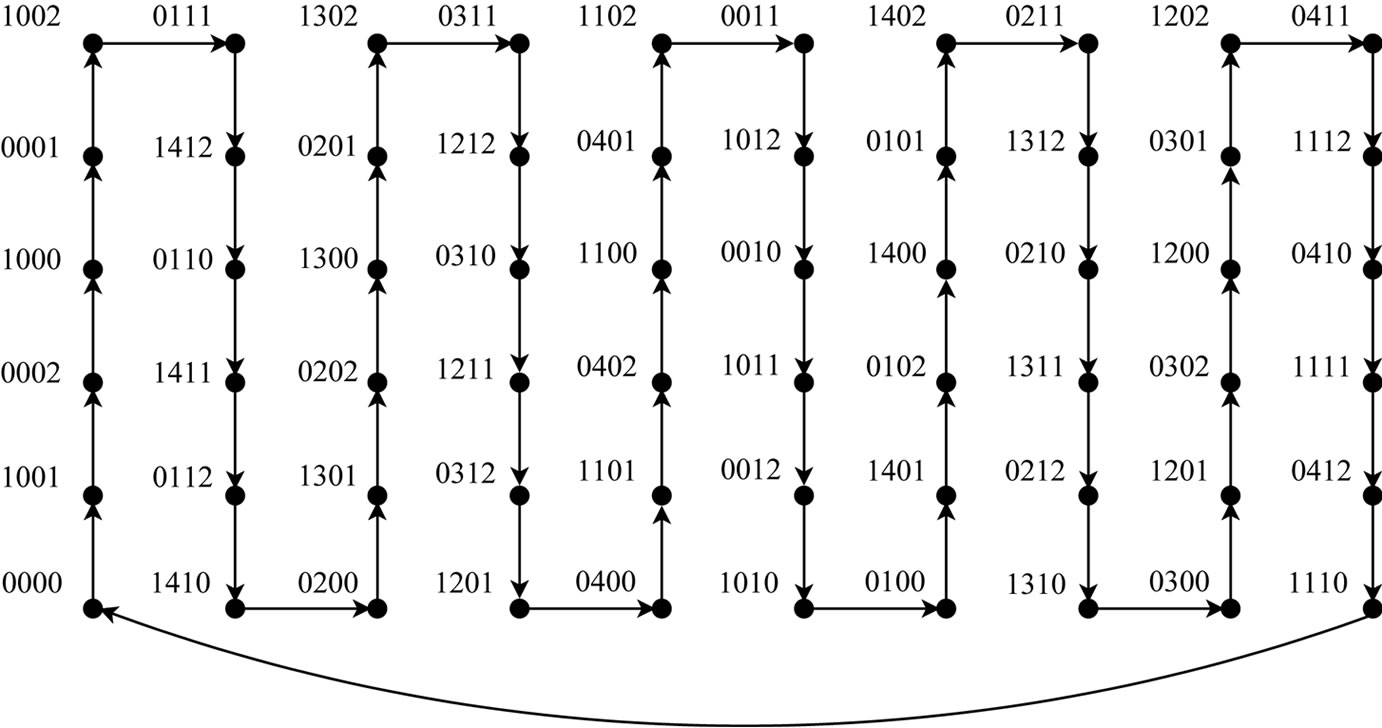
Figure 2. Hamilton cycle in the Cayley digraph on D10 × D6 with connection set . The label
. The label  denotes the vertex
denotes the vertex .
.

which reduces to the initial vertex v.
Finally, since the arc sequence  traces out a walk of length
traces out a walk of length 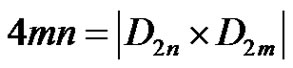 which is closed and visits every vertex of the digraph, we conclude that it is a Hamiltonian arc sequence. This arc sequence is shown in Figure 2 for the case where
which is closed and visits every vertex of the digraph, we conclude that it is a Hamiltonian arc sequence. This arc sequence is shown in Figure 2 for the case where  and
and .
.
REFERENCES
- S. Curran and J. Gallian, “Hamiltonian Cycles and Paths in Cayley Graphs and Digraphs—A Survey,” Discrete Mathematics, Vol. 156, No. 1-3, 1996, pp. 1-18. doi:10.1016/0012-365X(95)00072-5
- J. Gallian and D. Witte, “A Survey: Hamiltonian Cyles in Cayley Graphs,” Discrete Mathematics, Vol. 51, No. 3, 1984, pp. 293-304. doi:10.1016/0012-365X(84)90010-4
- K. Kutnar and D. Marušič, “Hamilton Cycles and Paths in Vertex-Transitive Graphs—Current Directions,” Dicrete Mathematics, Vol. 309, No. 17, 2009, pp. 5491-5500. doi:10.1016/j.disc.2009.02.017
- R. A. Rankin, “A Campanological Problem in Group Theory,” Proceedings of the Cambridge Philosophical Society, Vol. 44, No. 1, 1948, pp. 17-25. doi:10.1017/S030500410002394X
- W. Gaschütz, “Zu Einem von B. H. und H. Neumann Gestellten Problem,” Mathematische Nachrichten, Vol. 14, No. 4-6, 1955, pp. 249-252. doi:10.1002/mana.19550140406
NOTES
1The research of S. Gosselin was supported by the University of Winnipeg Board of Regents.

