Vol.3, No.1, 49-57 (2012) Journal of Biophysical Chemistry
http://dx.doi.org/10.4236/jbpc.2012.31007
Quantitative structure-property relationship (QS P R)
model for predicting acidities of ketones
Yunyun Yuan, Philip D. Mosier, Yan Zhang*
Department of Medicinal Chemistry, Virginia Commonwealth University, Richmond, USA;
*Corresponding Author:
Received 6 December 2011; revised 17 January 2012; accepted 29 January 2012
ABSTRACT
Ketones are one of the most common functional
groups, and ketone-containing compounds are
essential in both the nature and the chemical
sciences. As such, the acidities (pKa) of ketones
provide valuable information for scientists to
screen for biological activities, to determine
physical properties or to study reaction mecha-
nisms. Direct measurements of pKa of ketones
are not readily available due to their extremely
weak acidity. Hence, a quantitative structure-
property relationship (QSPR) model that can
predict the acidities of ketones and their acidity
order is highly desirable. The establishment of
an acidity scale in dimethyl sulfoxide (DMSO)
solution by Bordwell et al. made such an effort
possible. By utilizing the pKa values of forty-
eight ketones determined in DMSO as the training
set, a QSPR model for predicting acidities of
ketones was built by stepwise multiple linear re-
gression analysis. The established model showed
st atistical significance and predictiv e power (r2 =
0.91, q2 = 0.86, s = 1.42). Moreover, the QSPR
model also gave reasonable acidity predictions
for five ketones in an external pre diction set that
were not included in the model generation phase
(r2 = 0.92, s = 1.618). Overall, the reported QSPR
model for predicting acidities of ketones pro-
vides a useful tool for both biologists and che-
mists in understanding the biophysical proper-
ties and reaction rates of different classes of
ketones.
Keywords: QSPR; Acidity; Ketones; Linear
Regression
1. INTRODUCTION
Ketones play a crucial role in nature. For example,
metabolism of carbohydrates, fatty acids and amino acids
in humans and most vertebrates generates acetone, ace-
toacetate and beta-hydroxybutyrate, which are known as
ketone bodies in biochemistry. Acetoacetate and beta-
hydroxybutyrate are important fuels for many tissues.
For example, it was reported that acetoacetate contrib-
utes over 90% to the energy required for respiration in
the sheep heart, 85% in the sheep kidney cortex and 74%
in the sheep diaphragm [1]. Ketone bodies are also found
to have therapeutic values for neurological diseases such
as Alzheimer’s disease [2,3] and Parkinson’s disease [3,
4]. Hasebe and Hauptman et al. have discovered their
function in reducing epileptic seizures as well [5,6]. Ad-
ditionally, it was reported that monoacetoacetin (glycerol
monoacetoacetate) has the potential to decrease growth
of human gastric cancer cells [7].
Being inspired by their imperative role in nature, ke-
tones are also commonly applied scientifically and com-
mercially, especially in the field of chemistry. Not only
are they massively produced as solvents in industry, but
base-catalyzed condensation reactions with ketones are
also employed on a daily base in organic synthesis labs.
According to the reaction mechanism, in the presence of
a base, the chemoselectivity (relative reaction rates) or
regioselectivity (preferred reaction site), is primarily de-
termined by the acidities (pKa) of different ketones, i.e.
the acidities of alpha hydrogen atoms at different posi-
tions (Figure 1). Since ketones are extremely weak acids,
direct measurements of their acidities in hydroxylic sol-
vents seem to be impossible. Although measurements of
deuterium exchange rates along with some other methods
have determined the equilibrium acidities for a number
Figure 1. Alpha hydrogens at dif-
ferent positions may have different
acidities due to the effect of different
R group substituents (pKa(H1) ≠
pKa(H2)).

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57
50
of ketones [8-11], the accuracy and applicability were not
very satisfying. The establishment of an acidity scale in
dimethyl sulfoxide (DMSO) solution by Bordwell [12]
was undoubtedly a milestone in this respect. It provided
a large number of pKa values for a variety of weak acids
in DMSO, including ketones. With these pKa values as
well as the oxidation potentials of ketones and their con-
jugate bases, Bordwell et al. were able to predict both the
acidities of the radical cations formed from the parent
acids [13] and the homolytic bond dissociation energies
(BDEs) of their acidic C-H bonds [14]. BDEs are very
useful in terms of studying reaction mechanisms and
assessing stabilities of radicals [15]. Due to its simplicity
and general applicability, this method of calculating
BDEs is still being used today since it was first intro-
duced about twenty years ago [16].
Several groups have described QSPR models to pre-
dict pKa values of acids, alcohols, phenols, chlorinated
phenols and amines [17-23]. To our knowledge, no such
effort has been focused on the acidities of ketones yet.
Because ketones are so important both in nature and sci-
ence and because experimental determination of pKa
values is an exhausting process, the development of a
computational model that can accurately predict their
acidities is both valuable and timely. More specifically,
by utilizing such a QSPR model, biologists can easily
explore a variety of ketones that may carry comparable
pKa with the aforementioned ketone bodies to address the
same diseases based on the concept of “bioisosterism”,
whereas chemists can predict a reaction mechanism
where ketones are involved in order to design a more
reliable synthetic route for their target compounds. In
this report, we present a quantitative structure-property
relationship (QSPR) model to predict acidities of ketones
in DMSO. The effects of different functional groups and
substitution patterns on their acidity as represented by
five descriptors in the model are discussed.
2. MATERIALS AND METHODS
2.1. Data Set
Fifty-eight ketones with experimental pKa data [16,24,
25] were subjected to initial data screening. Three of the
ketones were first discarded to avoid incongruence of
data. Among them, two have markedly different struc-
tures (one is a quaternary ammonium salt and another is
a chromium tricarbonyl complex), while the pKa of the
third ketone was acquired under different condition. The
final set of fifty-five ketones (Figure 2) can be catego-
rized into three groups based on their structures. Group A
is composed of aliphatic noncyclic ketones 1 - 6. Group
B consists of cyclic ketones 7 - 17. The remaining ke-
tones 18 - 55, which typically contain at least one phenyl
ring in their structures and are exocyclic with respect to
the ketone, form the group C. Group C can be further
divided into five subgroups: C1, CH3COCHR1R2 (R1, R2
can be either same or different), 18 - 20; C2, CH3COR
(R is substituted or non-substituted aromatic ring), 21 -
33; C3, PhCOCH2R (R can be either aliphatic or aro-
matic), 34 - 51; C4, PhCOCHR1R2 (R1, R2 can either be
independent or form a cyclic ring), 52 - 54; C5, 55,
which falls into none of the above groups.
In order to evaluate how well a model to be built can
predict the acidities of ketones, an external prediction set
(PSET) that includes one or more members from each
group is considered necessary. The criteria for building
such a PSET were: 1) ketones which have either highest
(7) or lowest (39) pKa values are not eligible for the
PSET because a model cannot reliably predict properties
out of the range it was built, i.e. extrapolation; 2) the
qualified candidates for the PSET should be able to rep-
resent at least several of their group members or their
counterparts from other groups that share the same moie-
ties in their structures. For example, the effect on alpha
hydrogen acidity by replacing one hydrogen atom with a
methyl group can be calculated from comparing ketones
34 and 31. Similarly ketone 5 is qualified to enter the
PSET as long as ketone 1 remains in the training set
(TSET). In other words, those that have unique structures
were not considered for inclusion in the PSET. Based on
these guidelines and the size of each group, ketone 5
from group A, ketone 10 from group B, and ketones 20,
30, and 35 from group C were selected for the PSET. The
remaining fifty ketones were used as the training set to
generate the QSPR model.
2.2. Computational Details
The structures of the selected fifty-five ketones were
sketched and energy-minimized by SYBYL 8.1 [26] us-
ing the Tripos Force Filed and Gasteiger-Hückel charges
with a 0.05 kcal/(mol × Å) energy termination gradient,
dielectric constant ε = 1.0, and an 8.0 Å nonbonded in-
teraction (NB) cutoff. Molecular descriptors used for
describing the acidity and generating the QSPR equation
were calculated for each molecule using MDL QSAR
version 2.2.0.365. The stepwise multiple linear regres-
sion method was used to build the model. The number of
descriptors (n) in the equation was limited to no more
than the square root of the number of ketones in the
TSET minus 2 (n ≤ (TSET)0.5 – 2), which is 5 in this case.
The following criteria were considered when selecting the
descriptors: 1) higher F-statistic value introduced first; 2)
absolute t-statistic value not less than 3.5; 3) descriptors
should not be highly correlated with each other (intercor-
relation coefficient below 0.7); 4) no descriptors with
nly a few non-zero (or different) values. o

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57
51
Figure 2. Structures of the ketones employed in this study.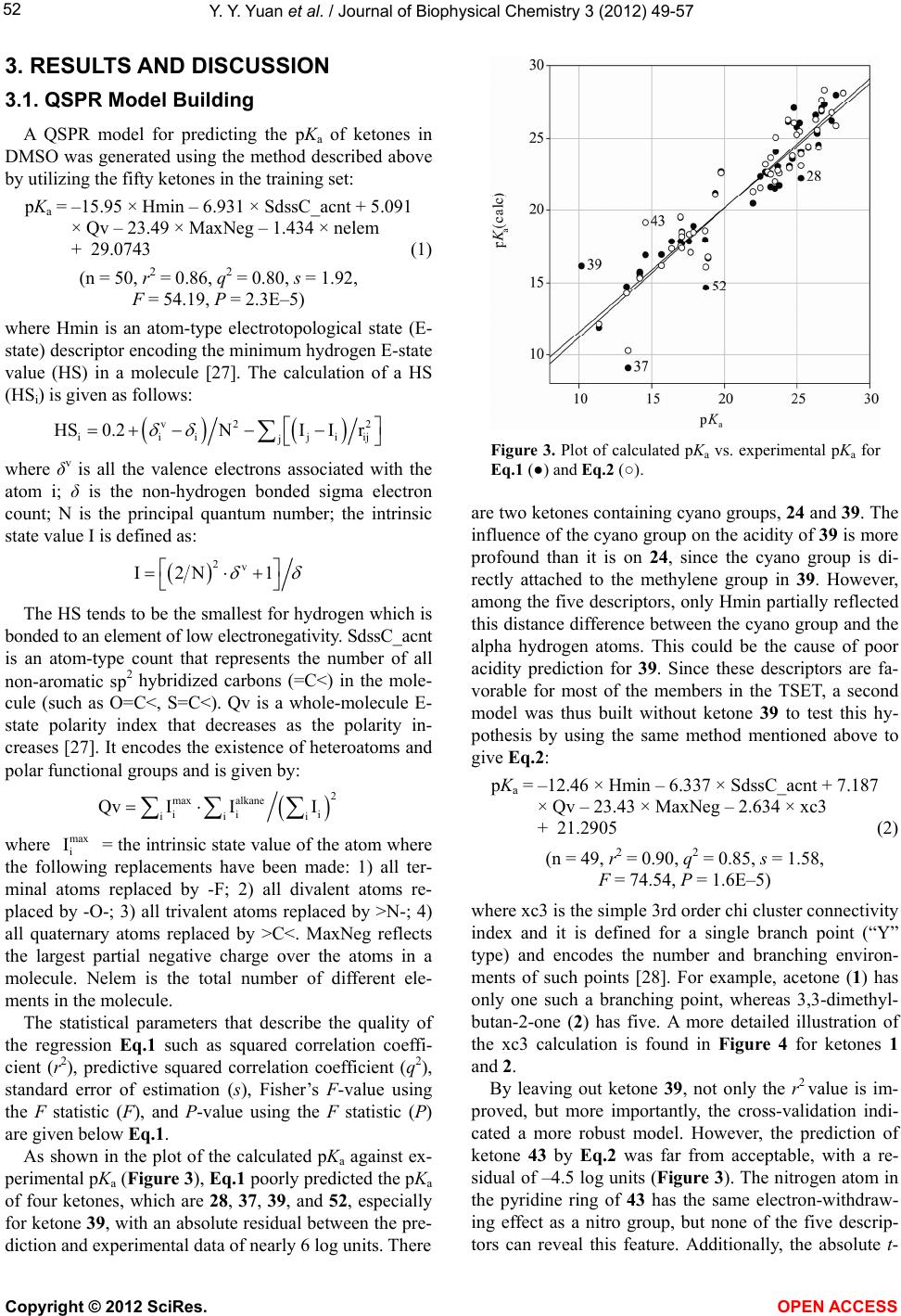

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57
52
3. RESULTS AND DISCUSSION
3.1. QSPR Model Building
A QSPR model for predicting the pKa of ketones in
DMSO was generated using the method described above
by utilizing the fifty ketones in the training set:
pKa = –15.95 × Hmin – 6.931 × SdssC_acnt + 5.091
× Qv – 23.49 × MaxNeg – 1.434 × nelem
+ 29.0743 (1)
(n = 50, r2 = 0.86, q2 = 0.80, s = 1.92,
F = 54.19, P = 2.3E–5)
where Hmin is an atom-type electrotopological state (E-
state) descriptor encoding the minimum hydrogen E-state
value (HS) in a molecule [27]. The calculation of a HS
(HSi) is given as follows:


v2 2
ijiii ji
j
HS0.2NI Ir 

 


where δv is all the valence electrons associated with the
atom i; δ is the non-hydrogen bonded sigma electron
count; N is the principal quantum number; the intrinsic
state value I is defined as:

2v
I2N 1





The HS tends to be the smallest for hydrogen which is
bonded to an element of low electronegativity. SdssC_acnt
is an atom-type count that represents the number of all
non-aromatic sp2 hybridized carbons (=C<) in the mole-
cule (such as O=C<, S=C<). Qv is a whole-molecule E-
state polarity index that decreases as the polarity in-
creases [27]. It encodes the existence of heteroatoms and
polar functional groups and is given by:

2
max alkane
ii i
iii
Qv III
 
where = the intrinsic state value of the atom where
the following replacements have been made: 1) all ter-
minal atoms replaced by -F; 2) all divalent atoms re-
placed by -O-; 3) all trivalent atoms replaced by >N-; 4)
all quaternary atoms replaced by >C<. MaxNeg reflects
the largest partial negative charge over the atoms in a
molecule. Nelem is the total number of different ele-
ments in the molecule.
max
i
I
The statistical parameters that describe the quality of
the regression Eq.1 such as squared correlation coeffi-
cient (r2), predictive squared correlation coefficient (q2),
standard error of estimation (s), Fisher’s F-value using
the F statistic (F), and P-value using the F statistic (P)
are given below Eq.1.
As shown in the plot of the calculated pKa against ex-
perimental pKa (Figure 3), Eq.1 poorly predicted the pKa
of four ketones, which are 28, 37, 39, and 52, especially
for ketone 39, with an absolute residual between the pre-
diction and experimental data of nearly 6 log units. There
Figure 3. Plot of calculated pKa vs. experimental pKa for
Eq.1 (●) and Eq.2 (○).
are two ketones containing cyano groups, 24 and 39. The
influence of the cyano group on the acidity of 39 is more
profound than it is on 24, since the cyano group is di-
rectly attached to the methylene group in 39. However,
among the five descriptors, only Hmin partially reflected
this distance difference between the cyano group and the
alpha hydrogen atoms. This could be the cause of poor
acidity prediction for 39. Since these descriptors are fa-
vorable for most of the members in the TSET, a second
model was thus built without ketone 39 to test this hy-
pothesis by using the same method mentioned above to
give Eq.2:
pKa = –12.46 × Hmin – 6.337 × SdssC_acnt + 7.187
× Qv – 23.43 × MaxNeg – 2.634 × xc3
+ 21.2905 (2)
(n = 49, r2 = 0.90, q2 = 0.85, s = 1.58,
F = 74.54, P = 1.6E–5)
where xc3 is the simple 3rd order chi cluster connectivity
index and it is defined for a single branch point (“Y”
type) and encodes the number and branching environ-
ments of such points [28]. For example, acetone (1) has
only one such a branching point, whereas 3,3-dimethyl-
butan-2-one (2) has five. A more detailed illustration of
the xc3 calculation is found in Figure 4 for ketones 1
and 2.
By leaving out ketone 39, not only the r2 value is im-
proved, but more importantly, the cross-validation indi-
cated a more robust model. However, the prediction of
ketone 43 by Eq.2 was far from acceptable, with a re-
sidual of –4.5 log units (Figure 3). The nitrogen atom in
the pyridine ring of 43 has the same electron-withdraw-
ing effect as a nitro group, but none of the five descrip-
tors can reveal this feature. Additionally, the absolute t-

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57 53
Figure 4. Illustration of the xc3 descriptor cal-
culation. The digit (δ) near each atom indicates
the number of non-hydrogen atoms that is at-
tached to it. The xc3 descriptor for each mole-
cule is then calculated by the following function:
xc3 =


0.5
ijkl
 

. For ketone 1, xc3 = (1 ×
3 × 1 × 1)–0.5 = 0.57735, whereas for ketone 2,
xc3 = (1 × 3 × 1 × 4)–0.5 + (1 × 1 × 4 × 1)–0.5 +
(1 × 1 × 4 × 3)–0.5 + (1 × 1 × 4 × 3)–0.5 + (1 × 1 ×
4 × 3)–0.5 = 1.6547.
statistic values for both MaxNeg and xc3 in Eq.2 are
below 3.5 (data not shown). This is important because
the t-statistic indicates the significance of each individual
descriptor in the linear regression equation. A third model
(Eq.3) was thus built after leaving out 43 to improve the
t-statistic by following the same procedure stated above
as:
pKa = –11.42× Hmin – 6.365 × SdssC_acnt + 7.487 × Qv
– 3.274 × xc3 – 24.12 × MaxNeg + 20.5577 (3)
(n = 48, r2 = 0.91, q2 = 0.86, s = 1.42,
F = 89.54, P = 3.6E–6)
Although there was not much difference for r2 and q2
between Eq.2 and Eq.3, the F statistic is modestly im-
proved along with the t-statistic for each descriptor (Ta-
ble 1). Among the five descriptors, the t values for
Hmin, SdssC_acnt and Qv are each above 4.0 and all t
values are ≥3.5, which implies that these descriptors
contribute significantly to the model. Furthermore, to
check the validity of the selected descriptor set (Hmin,
SdssC_acnt, Qv, xc3, and MaxNeg), 100 randomizations
of the dependent variable values among the training set
were carried out. Values of the multiple r2 were com-
puted for each of corresponding regressions. The mean
of r2 was 0.11. The mean square deviation of r2 value
was 0.058, indicating that the model was not arrived at
merely by chance.
High F, low s, a P value near 0, and r2 and q2 values
near 1 all indicate a reasonable QSPR model. In general,
a QSPR model is considered significant when P < 0.001
[29]. The established QSPR model (Eq.3) thus shows a
significant statistical quality, both in a reliability (r2 =
0.91) and a predictability (q2 = 0.86). The following dis-
cussion will therefore focus only on Eq.3.
A correlation plot of the calculated pKa against ex-
perimental pKa for Eq.3 is shown in Figure 5. The cal-
culated pKa values for each ketone in the TSET and cor-
relation matrix for the five descriptors can be found in
Tables 2 and 3 respectively. The absolute value of the
highest intercorrelation coefficient between any two of
the five descriptors in Ta b l e 3 is 0.6345 (Hmin to xc3),
which is below 0.7. As shown in Ta ble 2, the residuals
between calculated pKa and experimental pKa for over
70% of the TSET (thirty-four ketones out of forty-eight
in total) are smaller than standard error of estimation. In
general, the equation gave better prediction for group C2
(CH3COR), followed by group B (cyclic ketones) and
group C3 (PhCOCH2R). This is not surprising since the
group sizes of these three groups are much larger than
others, which let them take a leading role in selecting
descriptors that are more favorable for them. In most of
the groups, pKa values for ketones that show a distin-
guishable structure than other members are not very well
predicted by the model (e.g. ketones 2, 15, and 28). In
addition, it seems that the effect of substitutions is not
additive: if two identical functional groups are present in
a molecule, the pKa doesn’t simply change twice as much
compared to a molecule containing only one of such.
This is illustrated by the two series of ketones 1→18→
55 and 3→38→37.
3.2. Interpretation of Ketone Acidity
As pointed out by Bordwell et al. [25], acidity changes
observed for ketones by different substituents are mainly
Table 1. Mean, standard deviation (SD) and t-statistic (t) for
variables in Eq.3.
pKaQv MaxNeg xc3 SdssC_acnt Hmin
Mean 21.671.13–0.419 0.798 1.064 0.701
SD 4.470.190.0370 0.339 0.247 0.227
t NAa4.62–3.472 –3.557 –7.467 –7.474
aNA = Not applicable.
Figure 5. Plot of calculated pKa (Eq.3) vs. experimental
pKa for training set (●) and predicting set (○).

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57
54
Table 2. Calculated descriptor and pKa values (Eq.3) for ketones employed in this study.
Compd. Qv MaxNeg xc3 SdssC_acnt Hmin pKa (calc) pKa (exp) Residual Set Type
1 1.18837 –0.363773 0.57735 1 0.495833 24.3131 26.5 2.187 TSET
2 1.71171 –0.362911 1.6547 1 0.447569 25.2345 27.7 2.466 TSET
3 0.921785 –0.362257 0.816497 2 0.589958 14.0578 13.3 –0.7578 TSET
4 0.910359 –0.362154 0.696923 2 0.523632 15.1185 14.2 –0.9185 TSET
5 1.38932 –0.363201 0.288675 1 0.411125 27.7148 27.1 –0.6148 PSET
A
6 1.72295 –0.362625 0.859117 1 0.441347 27.9874 28.2 0.2126 TSET
7 0.926293 –0.363181 0.288675 1 0.440625 23.912 25.3 1.388 TSET
8 1.04132 –0.363182 0.288675 1 0.462847 24.5195 25.8 1.28 TSET
9 1.13987 –0.363182 0.288675 1 0.430569 25.6259 26.4 0.7741 TSET
10 1.22499 –0.363182 0.288675 1 0.443069 26.1192 27.8 1.6808 PSET
11 1.29913 –0.363182 0.288675 1 0.427722 26.8508 27.4 0.5492 TSET
12 1.42173 –0.363182 0.288675 1 0.427536 27.7709 26.7 –1.071 TSET
13 1.51875 –0.363182 0.288675 1 0.428395 28.4874 26.9 –1.587 TSET
14 0.992438 –0.444381 0.538452 1 0.677375 22.845 23 0.155 TSET
15 0.979818 –0.449867 0.816229 1 0.874486 19.723 17 –2.723 TSET
16 1.01571 –0.452228 1.08839 1 0.951111 18.2827 17.1 –1.183 TSET
B
17 1.01571 –0.452207 1.09401 1 0.92667 18.5429 17.9 –0.6429 TSET
18 1.13081 –0.363127 0.612372 1 0.594142 22.6294 19.8 –2.829 TSET
19 1.14996 –0.362471 0.777778 1 0.692451 21.093 19.4 –1.693 TSET
C1
20 0.817223 –0.360885 1.60306 1 0.706621 15.6978 12.5 –3.1978 PSET
21 1.03258 –0.440311 0.788675 1 0.646047 22.5859 23.8 1.214 TSET
22 1.03258 –0.440311 0.788675 1 0.652433 22.513 23.2 0.687 TSET
23 1.14927 –0.448196 0.788675 1 0.644333 23.6693 23.2 –0.4693 TSET
24 1.04142 –0.457447 0.788675 1 0.642647 21.3198 22 0.6802 TSET
25 1.22222 –0.444696 0.788675 1 0.550583 25.2015 25 –0.2015 TSET
26 1.22222 –0.444696 0.788675 1 0.532923 25.4031 25.2 –0.2031 TSET
27 1.50044 –0.439044 1.20452 1 0.548923 25.8057 24.8 –1.006 TSET
28 1.04142 –0.457447 0.788675 1 0.642647 23.1043 25.3 2.196 TSET
29 1.09917 –0.435697 0.704124 1 0.665776 23.0247 24.5 1.475 TSET
30 1.09917 –0.428801 0.704124 1 0.655976 22.9683 25.7 2.7317 PSET
31 1.0651 –0.439062 0.5 1 0.628361 23.9463 24.7 0.7537 TSET
32 1.09295 –0.445689 0.772166 1 0.680545 22.8278 23.7 0.8722 TSET
C2
33 1.10829 –0.448904 1.04994 1 0.732728 21.515 22.5 0.985 TSET
34 1.13081 –0.43878 0.402369 1 0.488934 26.343 24.4 –1.943 TSET
35 1.05257 –0.438425 0.606493 1 0.915111 20.2119 17.7 –2.5119 PSET
36 1.09714 –0.444395 0.606493 1 0.775684 22.2841 23.5 1.216 TSET
37 0.908075 –0.443194 0.804738 2 1.05672 10.6166 13.4 2.783 TSET
38 0.917396 –0.443207 0.810617 2 0.650357 15.3071 14.2 –1.107 TSET
40 0.830623 –0.44186 1.59718 1 1.20175 12.1195 11.4 –0.7195 TSET
41 1.25082 –0.443047 0.810617 1 0.573968 25.037 23.55 –1.487 TSET
42 1.02249 –0.441973 0.402369 1 0.676746 23.4647 22.85
–0.6147 TSET
44 1.08644 –0.438425 1.27316 1 0.996096 17.3608 16.4 –0.9608 TSET
45 1.08644 –0.438425 1.14395 1 1.06836 16.9588 18.9 1.941 TSET
46 1.08644 –0.438425 1.21199 1 0.996096 17.5611 17 –0.5611 TSET
C3
47 1.08644 –0.438425 1.21199 1 1.00519 17.4573 17.1 –0.3573 TSET
48 1.08644 –0.438425 1.14395 1 1.04392 17.2378 17.7 0.4622 TSET
49 1.08031 –0.438425 1.42734 1 1.05132 16.1796 15.7 –0.4796 TSET
50 1.0727 –0.438425 0.871785 1 0.991736 18.6218 17.6 –1.022 TSET
C3
51 1.0727 –0.438425 0.939826 1 0.967295 18.6781 17.1 –1.578 TSET
52 1.08506 –0.43778 0.803561 1 1.19256 16.6292 18.75 2.121 TSET
53 1.26181 –0.444132 0.69245 1 0.511156 26.2495 26.3 0.05051 TSET
C4
54 1.2096 –0.444113 0.525783 1 0.465708 26.9227 26.7 –0.2227 TSET
C5 55 1.09714 –0.36248 0.696923 1 0.880892 18.8109 18.7 –0.1109 TSET

Y. Y. Yuan et al. / Journal of Biophysical Chemistry 3 (2012) 49-57 55
Table 3. Correlation matrix (r values) for descriptors in Eq.3.
pKa Qv MaxNeg xc3 SdssC_acntHmin
pKa 1
Qv 0.628 1
MaxNeg 0.2247 0.3353 1
xc3 –0.5299 0.0181 –0.3723 1
SdssC_acnt –0.4585 –0.3003 0.21 –0.01812 1
Hmin –0.7548 –0.4545 –0.5028 0.6345 –0.1316 1
a balance among three effects: 1) steric effect on reso-
nance and solvation of the anion; 2) stabilizing effect on
the enolate ion either through delocalization or induction;
and 3) lone-pair-lone-pair electron repulsions.
Among the five descriptors in Eq.3, Qv is positively
correlated with pKa, and the other four descriptors con-
tribute negatively to the pKa value, especially Hmin. Be-
ing developed to encode both the electronic and steric
attributes of atoms in a molecule, two indices might be
expected to successfully capture the features influencing
pKa as noted in the previous paragraph. Indeed, the E-
state index Hmin was selected as one of the most sig-
nificant descriptors in the model. As shown in Ta ble 2,
except for 44 and 46, the ketones have unique Hmin
values. Furthermore, Hmin is significantly inversely cor-
related with pKa (Table 3) and ketones that have Hmin
values larger than 0.8 (e.g. 15 - 17, 37, 40, etc.) tend to
be more acidic (observed pKa values are among 11.4 to
18.9). Therefore these compounds are well predicted. A
more specific example could be illustrated by comparing
21 to 22. Having identical values for the other four de-
scriptors, the differences in their Hmin properties de-
cided the variations in their pKa values. The meta-chloro
group in 22 generates a stronger induced electron with-
drawing effect on the enolate ion than the para-chloro
group in 21 does, and hence 22 is more acidic than 21.
The steric effect reflected by Hmin is exemplified by
comparing 16 to 17 (although 16 and 17 don’t have ex-
actly matching MaxNeg and xc3 values, the role of both
descriptors is quite insignificant comparing to Hmin, in
this case). As suggested by their 3D structures, atoms C2,
C2a and C3 are not in the same plane as the C4-C10 at-
oms, and this generates a more hindered environment for
the methylene group in 17 than the one in 16. Since
steric effect contributes negatively to the acidity, 16 is
more acidic than 17. On the other hand, Hmin seemed
not sufficient to evaluate the acidity of polycyclic aro-
matic ketones. For example, although 48 is more acidic
than 45, 45 shows a higher Hmin value than 48 in spite
of the fairly strong inverse relationship between pKa and
Hmin (see Table 2).
The impact of SdssC_acnt on ketones acidities can be
easily observed for 3 - 4 and 37 - 38 compared to the rest
of the ketones. The SdssC_acnt values for these four ke-
tones are 2, two times of those for other ketones (Table
2), which makes them quite acidic as demonstrated by
the lower pKa of 3 and 38 than 1 and 31 respectively.
This was due to the additional electron withdrawing ef-
fect contributed by the second carbonyl group.
Not surprisingly, geometric and positional isomers
have the same Qv values (for example, 44 - 48). Among
the forty-eight ketones, only 3 - 4, 7, 37 - 38, and 40
have Qv values less than 0.95. It is not difficult to under-
stand that 3 - 4, and 37 - 38 are more polar due to the
presence of second carbonyl groups. Similarly, the sul-
fonyl group in 40 makes the molecule more polar. These
moieties are electron-withdrawing groups, which have a
stabilizing effect on the enolate ion through their induc-
tive stabilizing effect, and therefore the ketones contain-
ing these moieties are more acidic. Cyclobutanone 7 is
the most polar compound in the aliphatic cycloketones
category, and has the lowest pKa amongst them. On the
other hand this descriptor as well as others would not be
able to distinguish among different conformation of ke-
tones (such as cis vs. trans, chair vs. boat) and its influ-
ence to the acidity of the ketones.
Descriptor xc3 is an indicator of the degree of third
order branching, and thus implicates the effect of substi-
tution in a molecule. A molecule that is relatively com-
pact at some point(s) will have a higher xc3 value. There
are eleven ketones of which xc3 values are larger than 1
in the TSET. A critical aspect will have to be considered
when xc3 is involved to explain the acidities of ketones
in addition to the hindrance effect it causes, that is,
whether the branching at certain position(s) can stabilize
the enolate ion. This factor is perfectly demonstrated by
ketones 16 - 17, 44 - 49 and 40. The enolate ion for ke-
tone 40 is stabilized through inducing effect by sulfonyl
group, whereas the delocalization of the anion (the nega-
tive charge is distributed to the phenyl rings through
resonance) is achieved for ketones 16 - 17 and 44 - 49. In
contrast, the increased branching in ketone 2 can’t attain
either of the above effects, and this counts for its de-
creased acidity, compared to the less branching counter-
part 1. For ketone 2, the steric hindrance for the solvation
of its anion is the determining factor for pKa.
MaxNeg is a charge index. Most of the ketones carry
similar MaxNeg values. Interestingly, no matter what the
size of the cycloketones is, they share the same MaxNeg
value. More importantly, the MaxNeg values for ketones
in which the carbonyl groups are directly attached to a
phenyl ring are around –0.44. The MaxNeg values for
the remaining ketones are approximately –0.36. The re-
pulsion between the negatively charged carbonyl oxygen
and the aromatic pi-bonds, which is unfavorable for the
stability of the enolate ion, might be the reason that
MaxNeg contributes negatively to the pKa of the ketones,
a similar effect that lone-pair-lone-pair electron repul-

Y. Y. Yuan et al. / Journal of Biophysical C he m istry 3 (2012) 49-57
56
sions have.
3.3. Ketone Acidity Prediction
To further validate the built QSPR model, the gener-
ated regression Eq.3 was used to predict the pKa of the
five ketones in the external prediction set (Table 2). A
correlation plot of the calculated pKa against experimen-
tal pKa for the PSET is shown in Figure 5. A linear re-
gression was performed for the calculated pKa and the
experimental pKa. The statistics r2 and s are 0.92 and
1.618 respectively, which was considered to be satisfac-
tory. Table 2 showed that the QSPR model estimated the
acidity for those ketones with acceptable values while
the best prediction was obtained for compound 5. Com-
pound 20 is one of the only two ketones that carry a sul-
fonyl group, providing an explanation for the relatively
poor prediction.
The pKa shows a parabolic relationship with the ring
size of cycloketones 4 - 9, with the pKa of cyclohepta-
none 10 being the highest. However, cycloheptanone 10
wasn’t in the TSET when the model was built to reveal
this characteristic and hence none of the five descriptors
in the QSPR model Eq.3 can actually reflect this par-
ticular feature of cycloketones. Having a small number
of members among the whole training set also likely
confounded the prediction of the relative acidities of ke-
tones in this series, although the residuals for most cy-
cloketones are acceptable.
4. CONCLUSION
Ketones are important in both biochemistry and or-
ganic chemistry, and information about their pKa proper-
ties will be beneficial for both biologists and chemists.
The direct measurements of pKa of ketones are not avail-
able due to their extremely weak acidity. Hence, a QSPR
model which can be used to predict the acidities of ke-
tones is highly desirable. Fifty-five ketones of which the
pKa in DMSO were determined using the method devel-
oped by Bordwell were used to build such a QSPR
model. By leaving out two ketones (39 and 43) that show
unique structures from others, the training set of forty-
eight ketones in three main classes covering most func-
tional groups with an overall pKa in DMSO ranging from
11.4 to 28.2 is very well described by the statistically
significant regression Eq.3 (r2 = 0.91, q2 = 0.86, s =
1.42). Steps have been taken to ensure the quality of the
generated QSPR model in this paper. Importantly, the
five descriptors used to build the model are largely che-
mically intuitive and in agreement with the proposed
theory that describes the acidity of ketones, which further
strengthened the significance of the model. Moreover,
the QSPR model can reasonably predict the acidity of the
five ketones in the external prediction set (r2 = 0.92, s =
1.618). We anticipate that the model obtained will be
useful for prediction of ketone acidity that may be related
to their reactivity, reaction mechanism, and possibly
some biophysical properties in biological systems.
5. ACKNOWLEDGEMENTS
The authors thank Dr. Lemont B. Kier for his kind encouragement
and guidance during the study. Dr. Y. Y. would like to acknowledge the
Department of Medicinal Chemistry, Virginia Commonwealth Univer-
sity for providing excellent learning experience for all the postdoctoral
fellows.
REFERENCES
[1] Krebs, H.A. (1961) The physiological role of ketone
bodies. Biochemical Journal, 80, 225-233.
[2] Henderson, S.T. (2010) Ketone bodies as a therapeutic for
Alzheimer’s disease. RSC Drug Discovery Series, 2, 275-
306.
[3] Kashiwaya, Y., Takeshima, T., Mori, N., Nakashima, K.,
Clarke, K. and Veech, R.L. (2000) D-β-Hydroxybutyrate
protects neurons in models of Alzheimer’s and Parkin-
son’s disease. Proceedings of the National Academy of
Sciences of the United States of America, 97, 5440-5444.
doi:10.1073/pnas.97.10.5440
[4] Cornille, E., Abou-Hamdan, M., Khrestchatisky, M.,
Henderson, S.T., Nieoullon, A., De Reggi, M. and Gharib,
B. (2010) Enhancement of L-3-hydroxybutyryl-CoA de-
hydrogenase activity and circulating ketone body levels
by pantethine. Relevance to dopaminergic injury. BMC
Neuroscience, 11 , 51. doi:10.1186/1471-2202-11-51
[5] Hasebe, N., Abe, K., Sugiyama, E., Hosoi, R. and Inoue,
O. (2010) Anticonvulsant effects of methyl ethyl ketone
and diethyl ketone in several types of mouse seizure
models. European Journal of Pharmacology, 642 , 66-71.
doi:10.1016/j.ejphar.2010.05.036
[6] Hauptman, J.S. (2010) From the bench to the bedside:
Breaking down the blood-brain barrier, decoding the ha-
benula, understanding hand choice, and the role of ketone
bodies in epilepsy. Surgical Neurology International, 1,
86. doi:10.4103/2152-7806.74143
[7] Sawai, M., Yashiro, M., Nishiguchi, Y., Ohira, M. and
Hirakawa, K. (2004) Growth-inhibitory effects of the ke-
tone body, Monoacetoacetin, on human gastric cancer cells
with succinyl-CoA: 3-oxoacid CoA-transferase (SCOT)
deficiency. Anticancer Research, 24, 2213-2217.
[8] Novak, M. and Loudon, G.M. (1977) The pKa of aceto-
phenone in aqueous solution. Journal of Organic Chem-
istry, 42, 2494-2498. doi:10.1021/jo00434a032
[9] Chiang, Y., Kresge, A.J., Tang, Y.S. and Wirz, J. (1984)
The pKa and keto-enol equilibrium constant of acetone in
aqueous solution. Journal of the American Chemical So-
ciety, 106, 460-462. doi:10.1021/ja00314a055
[10] Chiang, Y., Kresge, A.J. and Wirz, J. (1984) Flash-ph-
otolytic generation of acetophenone enol. The ketoenol
equilibrium constant and pKa of acetophenone in aqueous

Y. Y. Yuan et al. / Journal of Biophysical C he m istry 3 (2012) 49-57
57
solution. Journal of the American Chemical Society, 106,
6392-6395. doi:10.1021/ja00333a049
[11] Pollack, R.M., Mack, J.P.G. and Eldin, S. (1987) Direct
observation of a dienolate intermediate in the base-cata-
lyzed isomerization of 5-androstene-3,17-dione to 4-and-
rostene-3,17-dione. Journal of the American Chemical
Society, 109, 5048-5050. doi:10.1021/ja00250a061
[12] Bordwell, F.G. (1988) Equilibrium acidities in dimethyl
sulfoxide solution. Accounts of Chemical Research, 21,
456-463. doi:10.1021/ar00156a004
[13] Bordwell, F.G. and Bausch, M.J. (1986) Radical cation
acidities in dimethyl sulfoxide solution. Journal of the
American Chemical Society, 108, 2473-2474.
doi:10.1021/ja00269a071
[14] Bordwell, F.G., Cheng, J.P., et al. (1988) Homolytic bond
dissociation energies in solution from equilibrium acidity
and electrochemical data. Journal of the American Che-
mical Society, 110, 1229-1231.
doi:10.1021/ja00212a035
[15] Lowry, T.H. and Richardson, K.S. (1981) Mechanism and
theory in organic chemistry. 2nd Edition, Harper and Row,
New York.
[16] Alnajjar, M.S., Zhang, X.-M., Gleicher, G.J., Truksa, S.V.
and Franz, J.A. (2002) Equilibrium acidities and homo-
lytic bond dissociation energies of acidic C-H bonds in
α-arylacetophenones and related compounds. Journal of
Organic Chemistry, 67, 9016-9022.
doi:10.1021/jo020275s
[17] Yu, H.-Y., Kühne, R., Ebert, R.-U. and Schüürman, G.
(2010) Comparative analysis of QSAR models for pre-
dicting pKa of organic oxygen acids and nitrogen bases
from molecular structure. Journal of Chemical Informa-
tion and Modeling, 50, 1949-1960.
doi:10.1021/ci100306k
[18] Eckert, F. and Klamt, A. (2006) Accurate prediction of
basicity in aqueous solution with COSMO-RS. Journal of
Computational Chemistry, 27, 11-19. doi:1002/jcc.20309
[19] Klamt, A., Eckert, F., Diedenhofen, M. and Beck, M.E.
(2003) First principles calculations of aqueous pKa values
for organic and inorganic acids using COSMO-RS reveal
an inconsistency in the slope of the pKa scale. Journal of
Physical Chemistry A, 107, 9380-9386.
doi:10.1021/jp034688o
[20] Liptak, M.D. and Shields, G.C. (2001) Accurate pKa Cal-
culations for carboxylic acids using complete basis set
and Gaussian-n models combined with CPCM continuum
solvation methods. Journal of the American Chemical
Society, 123, 7314-7319. doi:10.1021/ja010534f
[21] Schüürman, G., Cossi, M., Barone, V. and Tomasi, J.
(1998) Prediction of the pKa of carboxylic acids using the
ab initio continuum-solvation model PCM-UAHF. Jour-
nal of Physical Chemistry A, 102, 6706-6712.
doi:10.1021/jp981922f
[22] Schüürman, G. (1998) Quantum chemical analysis of the
energy of proton transfer from phenol and chlorophenols
to H2O in the gas phase and in aqueous solution. Journal
of Chemical Physics, 109, 9523-9528.
doi:10.1063/1.477614
[23] Schüürman, G. (1996) Modelling pKa of carboxylic acids
and chlorinated phenols. Quantitative Structure-Activity
Relationships, 15, 121-132.
doi:10.1002/qsar.19960150206
[24] Bordwell, F.G. and Harrelson, J.A. Jr. (1990) Acidities
and homolytic bond dissociation energies of the αC-H
bonds in ketones in DMSO. Canadian Journal of Chem-
istry, 68, 1714-1718. doi.org/10.1139/v90-266
[25] Bordwell, F.G., Harrelson, J.A. Jr. and Zhang, X.-M.
(1991) Homolytic bond dissociation energies of acidic
carbon-hydrogen bonds activated by one or two electron
acceptors. Journal of Organic Chemistry, 56, 4448-4450.
doi.org/10.1021/jo00014a022
[26] SYBYL 8.1, Tripos International, St. Louis, USA.
[27] Kier, L. and Hall, L. (1999) Molecular structure descrip-
tion: The electrotopological state. Academic Press, New
York.
[28] Kier, L. and Hall, L. (1986) Molecular connectivity in
structure-activity analysis. Research Studies Press, Chich-
ester.
[29] Liao, S.-Y., Xu, L.-C., Qian, L. and Zheng, K.-Ch. (2007)
QSAR and action mechanism of troxacitabine prodrugs
with antitumor activity. Journal of Theoretical & Com-
putational Chemistry, 6, 947-958.
doi:10.1142/S0219633607003428