Applied Mathematics
Vol.05 No.17(2014), Article ID:50913,7 pages
10.4236/am.2014.517268
A Mathematical Model for Schistosomiasis Japonicum with Harmless Delay
Huahua Cao, Shujing Gao*, Xiangyu Zhang, Youquan Luo
College of Mathematics and Computer Science, Gannan Normal University, Ganzhou, China
Email: 870577346@qq.com, *gaosjmath@126.com, xyzhang5@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 August 2014; revised 28 August 2014; accepted 16 September 2014
ABSTRACT
From the lifecycle of schistosome, the phenomenon of time delay is widespread. In this paper, a two-dimensional system is studied that incorporates two time delays which are the incubation period of human and snail, respectively. Our purpose is to demonstrate that the time delays are harmless for stability of equilibria of the system. Further, sufficient conditions of stability of equilibria are obtained.
Keywords:
Stability, Schistosomiasis Japonicum, Time Delay

1. Introduction
Mathematical models ([1] -[7] , etc.) have been used to study the transmission and control of schistosomiasis since the first model that has been given by MacDonald in [8] . MacDonald’s model consists of two differential equations in two state variables that correspond to average parasite burden in the definitive hosts and the prevalence of infection in snails. DAS et al. [5] added a layer of biological realism to these early models to study the delay effect on schistosomiasis transmission with control measures. The model is given by
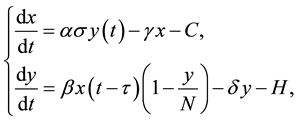 (1)
(1)
where 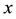 is the current number of egg laying schistosomes in the human host population and
is the current number of egg laying schistosomes in the human host population and 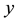 is the current number of infected snails in the environment. Here,
is the current number of infected snails in the environment. Here, 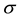 is the human population density per unit accessible water area;
is the human population density per unit accessible water area;  is the multiplication rate due to the infected snail population;
is the multiplication rate due to the infected snail population; 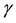 and
and 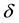 are the intrinsic death rates of two populations
are the intrinsic death rates of two populations  and
and 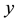 respectively;
respectively;  is the simple contact rate;
is the simple contact rate; 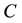 is the constant decay rate due to chemotherapy; and
is the constant decay rate due to chemotherapy; and 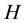 is the constant decay rate by predation or harvesting. Further
is the constant decay rate by predation or harvesting. Further 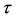 is the incubation period for becoming
is the incubation period for becoming  to be infectious. For simplicity, it is assumed that
to be infectious. For simplicity, it is assumed that 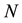 is the constant total population of snails.
is the constant total population of snails.
In [5] , for the sake of mathematical simplicity, they assumed the development of schistosoma is instantaneous. In fact, the developmental time of schistosome is not short. Under normal circumstances, the transit time from parasite eggs to miracidia to infect snail is about 21 days, cercariae are produced about 44 - 159 days after the miracidium penetration in snail hosts. In this paper, we also assume that 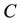 and
and 

where 

From biological view, we assume that system (2) holds for the time 

where
into

In the following, we focus on dynamics of system (2) in a nonnegative cone
It is well known by the fundamental theory of functional differential equations [9] that system (2) has a unique solution 


The remainder of the paper is organized as follows. In the next section, the stability of the disease-free equilibrium of system (2) is obtained. In Section 3, we investigate the stability of the endemic equilibrium. Some dynamical behaviors are given by numerical simulations in Section 4. This paper is ended with a brief discussion.
2. Stability Analysis of the Disease-Free Equilibrium
In this section, the stability of the disease-free equilibrium of system (2) is investigated.
Using standard methods, it is easy to see that the disease-free equilibrium 
Define the basic reproductive number by
Then for system (2), it is easy to obtain the following result:
(i) If

(ii) If


In the following, we study the global stability of the disease-free equilibrium 
Theorem 2.1. If

Proof. First, according to [9] , the Jacobian matrix at 

Then the characteristic equation of system (2) at

where



When

If





Assume that there exists a 

Separating real and image parts:
Adding up the squares of both equations, we obtain that

Note that
and 



Next, the global stability of the disease-free equilibrium of system (2) is analyzed. And the strategy of proof is to use Lyapunov functionals and the LaSalle invariance principle.
Theorem 2.2. If



Proof. Let 
Define

where
Calculating the derivative of 

Define

We derive from (8) and (9) that

Define

It follows from (10) and (11) that

On substituting 


If









which yields



3. Stability Analysis of the Endemic Equilibrium
It is obtained that the endemic equilibrium 


Similar to the proof of Theorem 2.1, the following result is obtained.
Theorem 3.1. If

Proof. First, according to [9] , the Jacobian matrix at 

Then the characteristic equation of system (2) at

where
When

If


Assume that there exists a 

Separating real and image parts:
Adding up the squares of both equations, we obtain that

We know that 



Now, we are interested in the global stability of
Theorem 3.2. If



Proof. It is easy to check that equilibrium 






When
It follows that
which leads to the nonexistence of periodic orbits by Bendixson theorem, therefore, 
4. Numerical Simulations
It is reported that cercariae are produced about 44 - 159 days after the miracidium penetration in snails. And the time from parasite eggs to miracidia to infect snail is about 21 days. Therefore, we choose 









Thus, we can obtain





From the above theorems, we know that the two time delays are harmless. According to the expression of
Figure 1. The figure (a) shows that a numerical solution of system (2) tends to the disease-free equilibrium as time tends to infinity, where 

Figure 2. Simulation results:

the impact of C and H on schistosomiasis transmission is discussed. Fixing




From the formula of the basic reproductive number, we know that the basic reproductive number is a decrease function of the rates of chemotherapy and predation or harvesting. This means chemotherapy and predation or harvesting can influence the system.
However, to find out the most influential control measure, we need sensitivity analysis. Now we carry out the sensitivity analysis by calculating the derivation of 


From Figure 4(a), we can see that when






Figure 3. Forward bifurcation diagrams for the parasite eggs population.
Figure 4. Sensitivity analysis of 


In brief, the basic reproductive number 


By sensitivity analysis of the basic reproductive number on the rates of chemotherapy and predation or harvesting, we know that the basic reproductive number is a decrease function of the rates of chemotherapy and predation or harvesting. In numerical simulations, we also find that the smaller of values of the rate of chemotherapy, the more sensitive of the basic reproductive number
Although the two time delays are harmless, all of these results imply that the rates of chemotherapy and predation or harvesting can influence the dynamic behaviors. Furthermore, to reduce the prevalence of schistosomiasis infection, to some extent, increasing the rate of predation or harvesting by some measures could achieve better results than increasing the rate of chemotherapy.
5. Conclusions
In this paper, we propose a system of delayed differential equations for schistosomiasis japonicum transmission and obtain sufficient conditions for the existence and local stability of equilibria. Further, global asymptotic stability of the disease-free equilibrium is also studied by constructing suitable Lyapunov functions. When



Finally, we guess that the endemic equilibrium should be global asymptotic stable when
Figure 5. Phase diagrams: (a)

Acknowledgements
The research has been partially supported by The Natural Science Foundation of China (No. 11261004), China Postdoctoral Science Foundation funded project (No.
Cite this paper
HuahuaCao,ShujingGao,XiangyuZhang,YouquanLuo, (2014) A Mathematical Model for Schistosomiasis Japonicum with Harmless Delay. Applied Mathematics,05,2807-2814. doi: 10.4236/am.2014.517268
References
- 1. Anderson, R.M. and May, R.M. (1985) Helminth Infections of Humans Mathematical Models, Population Dynamics, and Control. Advances in Parasitology, 24, 1-101.
http://dx.doi.org/10.1016/S0065-308X(08)60561-8 - 2. Barbour, A.D. (1996) Modeling the Transmission of Schistosomiasis: An Introductory View. The American Journal of Tropical Medicine and Hygiene, 55, 135-143.
- 3. Woolhouse, M.E. (1991) On the Application of Mathematical Models of Schistosome Transmission Dynamics. I. Natural Transmission. Acta Tropica, 49, 241-270.
http://dx.doi.org/10.1016/0001-706X(91)90077-W - 4. Yang, H.M. (2003) Comparison between Schistosomiasis Transmission Modeling Considering Acquired Immunity and Age-Structured Contact Pattern with Infested Water. Mathematical Biosciences, 184, 1-26.
http://dx.doi.org/10.1016/S0025-5564(03)00045-2 - 5. Das, P., Mukherjee, D. and Sarkar, A.K. (2006) A Study of Schistosome Transmission Dynamics and Its Control. Journal of Biological Systems, 14, 295-302.
http://dx.doi.org/10.1142/S0218339006001799 - 6. Chiyaka, E.T. and Garira, W. (2009) Mathematical Analysis of the Transmission Dynamics of Schistosomiasis in the Human-Snail Host. Journal of Biological Systems, 17, 397-423.
http://dx.doi.org/10.1142/S0218339009002910 - 7. Qi, L.X. and Cui, J. (2012) Modeling the Schistosomiasis on the Islets in Nanjing. International Journal of Biomathematics, 5, 189-205.
- 8. Macdonald, G. (1965) The Dynamics of Helminth Infections, with Special Reference to Schistosomes. Transactions of the Royal Society of Tropical Medicine and Hygiene, 59, 489-506.
http://dx.doi.org/10.1016/0035-9203(65)90152-5 - 9. Hale, J.K. (1976) Theory of Functional Differential Equations. Springer, New York.
NOTES
*Corresponding author.


























