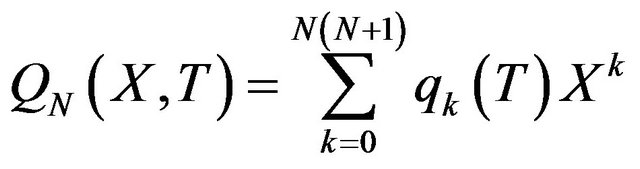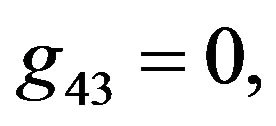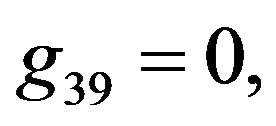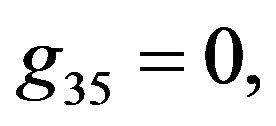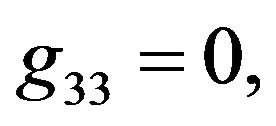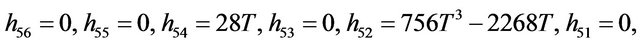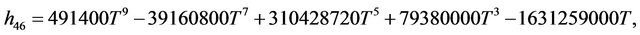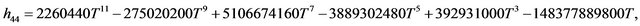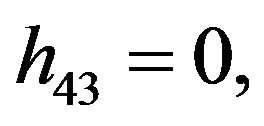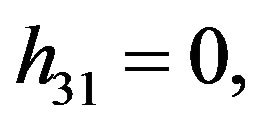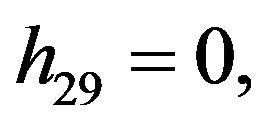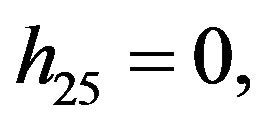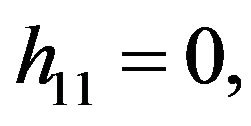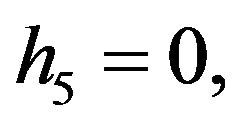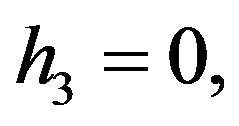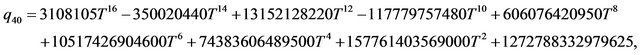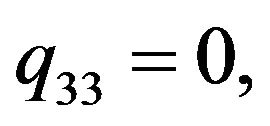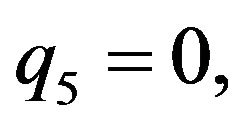Journal of Modern Physics
Vol.4 No.2(2013), Article ID:28330,21 pages DOI:10.4236/jmp.2013.42035
Wronskian Representation of Solutions of NLS Equation, and Seventh Order Rogue Wave
Université de Bourgogne, Dijon, France
Email: Pierre.Gaillard@u-bourgogne.fr
Received November 28, 2012; revised December 30, 2012; accepted January 8, 2013
Keywords: Riemann Theta Functions; Fredholm Determinant; Wronskian; NLS Equation; Peregrine Breathers; Akhmediev Solutions
ABSTRACT
In this paper, we use the representation of the solutions of the focusing nonlinear Schrödinger equation we have constructed recently, in terms of wronskians; when we perform a special passage to the limit, we get quasi-rational solutions expressed as a ratio of two determinants. We have already construct breathers of orders N = 4, 5, 6 in preceding works; we give here the breather of order seven.
1. Introduction
From fundamental work of Zakharov and Shabat in 1968 [1,2], a lot of research has been carried out on the nonlinear Schrödinger equation (NLS). The case of periodic and almost periodic algebro-geometric solutions to the focusing NLS equation were first constructed in 1976 by Its and Kotlyarov [3]. The first quasi-rational solutions of NLS equation were construted in 1983 by Peregrine [4]; they are nowadays called worldwide Peregrine breathers. In 1986, Eleonski, Akhmediev and Kulagin obtained the two-phase almost periodic solution to the NLS equation and obtained the first higher order analogue of the Peregrine breather [5,6]. Other families of higher order were constructed in a series of articles by Akhmediev et al. [7,8] using Darboux transformations.
In 2010, it has been shown in [9] that rational solutions of NLs equation can be writen as a quotient of two wronskians.
In this paper, we use a result [10] giving a new representation of the solutions of the NLS equation in terms of a ratio of two wronskians determinants of even order 2N composed of elementary functions; the related solutions of NLS are called of order N. When we perform the passage to the limit when some parameter tends to 0, we got families of multi-rogue wave solutions of the focusing NLS equation depending on a certain number of parameters. It allows to recognize the famous Peregrine breather [4] and also higher order Peregrine’s breathers constructed by Akhmediev [7,11].
Recently, another representation of the solutions of the focusing NLS equation, as a ratio of two determinants has been given in [12] using generalized Darboux transform.
A new approach has been done in [13] which gives a determinant representation of solutions of the focusing NLS equation, obtained from Hirota bilinear method, derived by reduction of the Gram determinant representation for Davey-Stewartson system.
We have already given breathers of order N = 1 to N = 6 in [14]. Here, we construct the breather of order N = 7 which shows the efficiency of this method.
2. Expression of Solutions of NLS Equation in Terms of Wronskian Determinant and Quasi-Rational Limit
2.1. Solutions of NLS Equation in Terms of Wronskian Determinant
We briefly recall results obtained in [10,14]. We consider the focusing NLS equation
 (1)
(1)
From [14], the solution of the NLS equation can be written in the form
 (2)
(2)
In (2), the matrix  is defined by
is defined by
 (3)
(3)
The terms  and
and 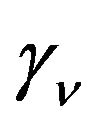 are functions of the parameters
are functions of the parameters  satisfying the relations
satisfying the relations
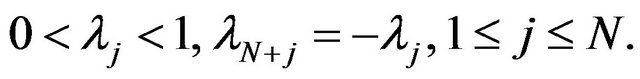
They are given by the following equations,

and
 .
.
The terms  are defined by
are defined by
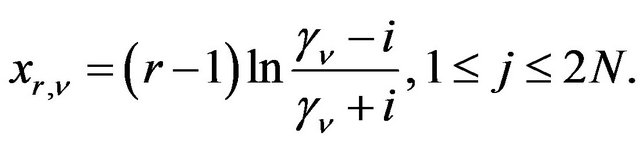
The coefficients  are defined by :
are defined by :
 (4)
(4)
We consider the following functions
 (5)
(5)
We use the following notations:
 .
.
 is the wronskian
is the wronskian
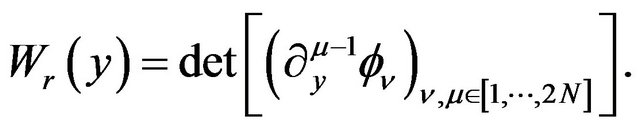 (6)
(6)
We consider the matrix  defined by
defined by
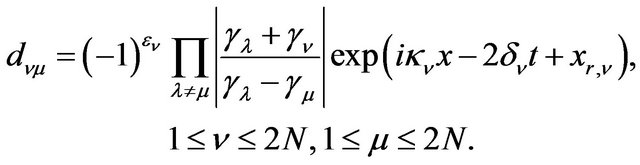
Then we get the following link between Fredohlm and Wronskian determinants [14]
Theorem 2.1
 (7)
(7)
where

It can be deduced the following result:
Theorem 2.2 The function v defined by
 (8)
(8)
is solution of the NLS Equation (1)

2.2. Quasi-Rational Solutions of NLS Equation
In the following, we take the limit when the parameters  for
for  and
and  for
for  .
.
For simplicity, we denote  the term
the term .
.
We consider the parameter  written in the form
written in the form
 (9)
(9)
When  goes to 0, we realize limited expansions at order p, for
goes to 0, we realize limited expansions at order p, for , of the terms
, of the terms








We have the central result formulated in [14] :
Theorem 2.3 The function v defined by
 (10)
(10)
is a quasi-rational solution of the NLS Equation (1)

Proof: Let  be the complex number
be the complex number
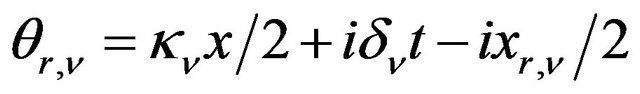 ,
,  ,
, . We use the following functions:
. We use the following functions:
 (11)
(11)
for , and
, and
 (12)
(12)
for .
.
We define the functions  for
for ,
,  in the same way, where the term
in the same way, where the term  in
in 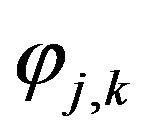 is replaced by
is replaced by .
.
Then it is clear that
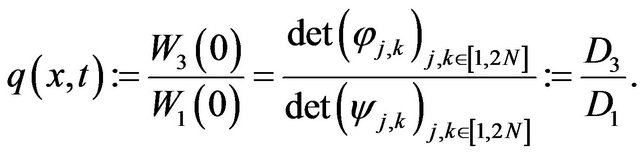 (13)
(13)
All the functions  and
and  and their derivatives depend on
and their derivatives depend on 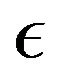 and can all be prolonged by continuity when
and can all be prolonged by continuity when .
.
For simplicity we denote  the term
the term
 ,
,  and
and  the term
the term .
.
Then we use the expansions
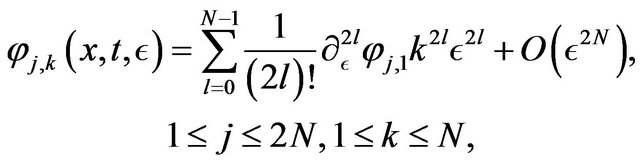

We have the same expansions for the functions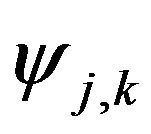 .
.


The components j of the columns 1 and N + 1 are respectively equal by definition to  for
for ,
, 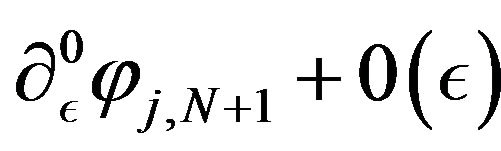 for
for  of
of , and
, and  for
for ,
, 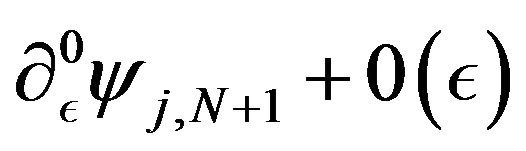 for
for  of
of .
.
At the first step of the reduction, we replace the columns 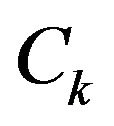 by
by  and
and  by
by  for
for , for
, for ; we do the same changes for
; we do the same changes for . Each component j of the column
. Each component j of the column  of
of  can be rewritten as
can be rewritten as

and the column  replaced by
replaced by

for . For
. For , we have the same reductions, each component j of the column
, we have the same reductions, each component j of the column  of can be rewritten as
of can be rewritten as

and the column  replaced by
replaced by

for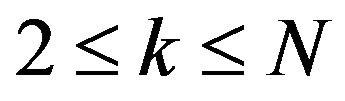 .
.
We can factorize in D3 and D1 in each column k and  the term
the term  for
for , and so simplify these common terms in numerator and denominator.
, and so simplify these common terms in numerator and denominator.
If we restrict the developments at order 1 in columns 2 and , we get respectively
, we get respectively  for the component j of D2,
for the component j of D2,  for the component j of
for the component j of  of D3, and
of D3, and  for the component j of
for the component j of ,
,  for the component j of
for the component j of 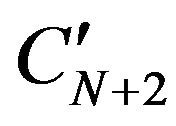 of D1. This algorithm can be continued until the columns CN, C2N of D3 and
of D1. This algorithm can be continued until the columns CN, C2N of D3 and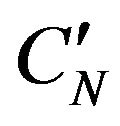 ,
, 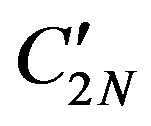 of D1.
of D1.
Then taking the limit when  tends to 0,
tends to 0,  can be replaced by
can be replaced by 
 (14)
(14)
Each element of these determinants is a polynomial in x and t. So the solution of the NLS equation takes the form  with
with  a rational function in x and t, and which ends the proof.
a rational function in x and t, and which ends the proof.
3. Seventh-Order Breather Solution of NLS Equation
3.1. Fiber-Optics Case
To get solutions of NLS equation written in the context of fiber optics
 (15)
(15)
from these of (1), we can make the following changes of variables
 (16)
(16)
Equation (15) plays a fundamental role in optics and is the object of active research as recent work [8] attests it where the solutions of the two-breathers are studied.
3.2. Case of the Initial Conditions
In the case of order N = 7, we make an expansion at order 13. Taking the limit when  with dj = j, 1 ≤ j ≤ N, the solution of NLS Equation (15) takes the form
with dj = j, 1 ≤ j ≤ N, the solution of NLS Equation (15) takes the form

Because of the length of the complete analytical expression, we only give it in the appendix.
We give here the expression of the solution in the form

in the case t = 0:




Figure 1. Solution to the NLS equation, N = 7.
Remark 3.1 The expressions of  and
and 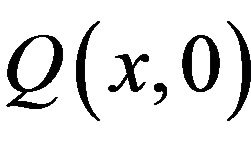 can be easily verified from the recursive formulae given in [11].
can be easily verified from the recursive formulae given in [11].
3.3. Plot in the (x, t) Coordinates
Please see Figure 1.
4. Conclusion
The method described in the present paper provides a powerful tool to get explicitly solutions of the NLS equation.
To the best of my knowledge, it is the first time that the breather of order seven solution of the NLS equation is presented.
It confirms the conjecture about the shape of the rogue wave in the  coordinates, the maximum of amplitude equal to 2N + 1 = 15 and the degree of polynomials in x and t here equal to 56 as already formulated in [7]. This new formulation gives the possibility, by introduction of parameters in the arguments of preceding functions defined in the text, to create an infinite set of non singular solutions of NLS equation. It will be the next step of the work which will open a large way to future researches in this domain.
coordinates, the maximum of amplitude equal to 2N + 1 = 15 and the degree of polynomials in x and t here equal to 56 as already formulated in [7]. This new formulation gives the possibility, by introduction of parameters in the arguments of preceding functions defined in the text, to create an infinite set of non singular solutions of NLS equation. It will be the next step of the work which will open a large way to future researches in this domain.
REFERENCES
- V. E. Zakharov, “Stability of Periodic Waves of Finite Amplitude on a Surface of a Deep Fluid,” Journal of Applied Mechanics and Technical Physics, Vol. 9, No. 2, 1968, pp. 86-94.
- V. E. Zakharov and A. B. Shabat, “Exact Theory of Two Dimensional Self-Focusing and One Dimensinal SelfModulation of Waves in Nonlinear Media,” Soviet Physics—JETP, Vol. 34, 1972, pp. 62-69.
- A. R. Its and V. P. Kotlyarov, “Explicit Expressions for the Solutions of Nonlinear Schrödinger Equation,” Docklady Akademii Nauk SSSR, Vol. 965, No. 11, 1976, pp. 965-968.
- D. Peregrine, “Water Waves, Nonlinear Schrödinger Equations and Their Solutions,” Journal of the Australian Mathematical Society, Vol. 25, 1983, pp. 16-43.
- N. Akhmediev, V. Eleonsky and N. Kulagin, “Generation of Periodic Trains of Picosecond Pulses in an Optical Fiber: Exact Solutions,” Soviet Physics—JETP, Vol. 62, 1985, pp. 894-899.
- N. Akhmediev, V. Eleonskii and N. Kulagin, “Exact First Order Solutions of the Nonlinear Schrödinger Equation,” Theoretical and Mathematical Physics, Vol. 72, No. 2, 1988, pp. 809-196. doi:10.1007/BF01017105
- N. Akhmediev, A. Ankiewicz and J. M. Soto-Crespo, “Rogue Waves and Rational Solutions of Nonlinear Schrödinger Equation,” Physical Review E, Vol. 80, 2009, Article ID: 026601.
- D. J. Kedziora, A. Ankiewicz and N. Akhmediev, “Circular Rogue Wave Clusters,” Physical Review E, Vol. 84, 2011, Article ID: 056611.
- P. Dubard, P. Gaillard, C. Klein and V. B. Matveev, “On Multi-Rogue Waves Solutions of the NLS Equation and Position Solutions of the KdV Equation,” European Physical Journal, Vol. 185, No. 1, 2010, pp. 247-258. doi:10.1140/epjst/e2010-01252-9
- P. Gaillard, “Families of Quasi-Rational Solutions of the NLS Equation and Multi-Rogue Waves,” Journal of Physics A: Mathematical and Theoretical, Vol. 44, No. 43, 2011, pp. 1-15. doi:10.1088/1751-8113/44/43/435204
- A. Ankiewicz, N. Akhmediev and P. A. Clarkson, “Rogue Waves, Rational Solutions, the Patterns of Their Zeros and Integral Relations,” Journal of Physics A: Mathematical and Theoretical, Vol. 43, 2010, pp. 1-9
- B. Guo, L. Ling and Q. P. Liu, “Nonlinear Schrödinger Equation: Generalized Darboux Transformation and Rogue Wave Solutions,” Physical Review E, Vol. 85, No. 2, 2012, Article ID: 026607. doi:10.1103/PhysRevE.85.026607
- Y. Ohta and J. Yang, “General High-Order Rogue Waves and Their Dynamics in the Nonlinear Schrödinger Equation,” Proceedings of the Royal Society A, Vol. 468, No. 2142, 2012, pp. 1716-1740. doi:10.1098/rspa.2011.0640
- P. Gaillard, “Wronskian Representation of Solutions of the NLS Equation and Higher Peregrine Breathers,” Journal of Mathematical Sciences: Advances and Applications, Vol. 13, No. 2, 2012, pp. 71-153.
Appendix
Rather than to give the analytical expression in the form , to shorten the formulation one prefers to give that inspired by Akhmediev et al. in [11].
, to shorten the formulation one prefers to give that inspired by Akhmediev et al. in [11].
The solution of NLS equation takes the form, with N = 7

with