Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56787,24 pages
10.4236/jamp.2015.35072
Exact Quasi-Classical Asymptotic beyond Maslov Canonical Operator and Quantum Jumps Nature
Jaykov Foukzon1, Alex Potapov2, Stanislav Podosenov3
1Israel Institute of Technology, Haifa, Israel
2The Institute of Radioengineering and Electronics (IRE) of Russian Academy of Sciences, Moscow, Russian
3All-Russian Scientific-Research Institute, Moscow, Russian
Email: jaykovfoukzon@list.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 February 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
Exact quasi-classical asymptotic beyond WKB-theory and beyond Maslov canonical operator to the Colombeau solutions of the n-dimensional Schrodinger equation is presented. Quantum jumps nature is considered successfully. We pointed out that an explanation of quantum jumps can be found to result from Colombeau solutions of the Schrödinger equation alone without additional postulates.
Keywords:
Quantum Jumps, Quantum Measurements Theory, Quantum Averages, Limiting Quantum Trajectory, Schrodinger Equation, Stochastic Quantum Jump Equation, Colombeau Solution, Feynman Path Integral, Maslov Canonical Operator, Feynman-Colombeau Propagator

1. Introduction
A number of experiments on trapped single ions or atoms have been performed in recent years [1] - [4] . Monitoring the intensity of scattered laser light off of such systems has shown abrupt changes that have been cited as evidence of “quantum jumps” between states of the scattered ion or atom. The existence of such jumps was required by Bohr in his theory of the atom. Bohr’s quantum jumps between atomic states [5] were the first form of quantum dynamics to be postulated. He assumed that an atom remained in an atomic eigenstate until it made an instantaneous jump to another state with the emission or absorption of a photon. Since these jumps do not appear to occur in solutions of the Schrodinger equation, something similar to Bohr’s idea has been added as an extra postulate in modern quantum mechanics.
Stochastic quantum jump equations [6] - [8] were introduced as a tool for simulating the dynamics of a dissipative system with a large Hilbert space and their links with quantum measurement theory were also noted [9] - [13] . This measurement interpretation is generally known as quantum trajectory theory [14] . By adding filter cavities as part of the apparatus, even the quantum jumps in the dressed state model can be interpreted as approximations to measurement-induced jumps [15] .
The question arises whether an explanation of these jumps can be found to result from a Colombeau solution [16] - [18] 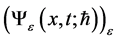 of the Schrödinger equation alone without additional postulates. We found exact quasi-classical asymptotic of the quantum averages with position variable with localized initial data.
of the Schrödinger equation alone without additional postulates. We found exact quasi-classical asymptotic of the quantum averages with position variable with localized initial data.
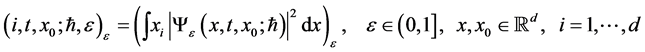 (1.1)
(1.1)
i.e. we found the limiting Colombeau quantum averages (limiting Colombeau quantum trajectories) such that [18] :
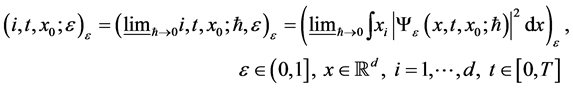 (1.2)
(1.2)
and limiting quantum trajectories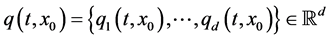 ,
, 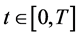 such that
such that
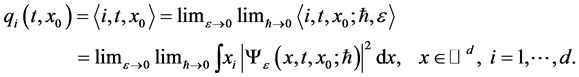 (1.3)
(1.3)
if limit in LHS of Equation (1.3) exists.
The physical interpretation of these asymptotic given below, shows that the answer is “yes” for the limiting quantum trajectories with localized initial data.
Note that an axiom of quantum measurement is: if the particle is in some state 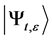 that the probability
that the probability  of getting a result
of getting a result 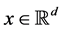 at instant
at instant  with an accuracy of
with an accuracy of 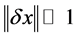 will be given by
will be given by
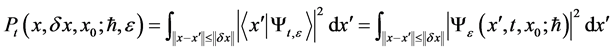 . (1.4)
. (1.4)
We rewrite now Equation (1.4) of the form
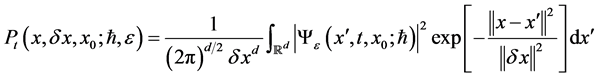 (1.5)
(1.5)
We define well localized limiting quantum trajectories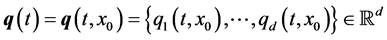 ,
,
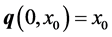 ,
, 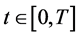 such that:
such that:

and well localized limiting quantum trajectories



if limit in LHS of Equation (1.7) exists.
2. Colombeau Solutions of the Schrödinger Equation and Corresponding Path Integral Representation
Let 


Let us consider Schrödinger equation:


Here operator 


Theorem 2.1. [19] [20] . Assume that: (1)



where we have set 

where







where we have set 1) 


Trotter and Kato well known classical results give a precise meaning to the Feynman integral when the potential 

We avoided this difficulty using contemporary Colombeau framework [16] - [18] . Using replacement




Potential


1)

Here 
Finally we obtain regularized Schrödinger equation of Colombeau form [21] - [24] :


Using the inequality (2.7) Theorem 2.1 asserts again that corresponding solution of the Schrödinger Equations (2.8)-(2.9) exist and can be represented via formulae:

where we have set 

where we have set
We rewrite Equation (2.10) for a future application symbolically of the following form

or of the following form

For the limit in RHS of (2.12) and (2.13) we will be used canonical path integral notation

where
Substitution 

(2.15)
We rewrite Equation (2.15) for a future application symbolically of the following form

or of the following form

For the limit in RHS of (2.16) and (2.17) we will be used following path integral notation

Let us consider now regularized oscillatory integral

Lemma 2.1. (Localization Principle [25] [26] ) Let 









Then 


Lemma 2.2. (Generalized Localization Principle) Let 








Then there exist infinite sequence


Proof. Equality (2.23) immediately follows from (2.21).
Remark 2.1. From Lemma 2.2 follows that stationary phase approximation is not a valid asymptotic approximation in the limit 
3. Exact Quasi-Classical Asymptotic Beyond Maslov Canonical Operator
Theorem 3.1. Let us consider Cauchy problem (2.8) with initial data 

where 

1) We assume now that: a)





2) Let 


Here


3) Let 

where master Lagrangian 


Let 

4) Let 

Assume that: for a given values of the parameters 
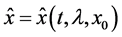

Thus one can to calculate the limiting quantum trajectory corresponding to potential 

Proof. From inequality (A.15) and Theorem A1, using inequalities (A.53.a) and (A.53.b) we obtain

where


We note that

where


and


From Equation (3.18) one obtain

where


Let us calculate now path integral 




and

From Equation (3.17) and Equation (3.24) we obtain

Substitution Equation (3.25) into Equation (3.26) gives

Similarly one obtain

Let us calculate now integral 





Substitution Equations (3.28)-(3.29) into Equation (3.21) gives
(3.30)
Substitution Equation (3.30) into Equation (3.16) gives

Similarly one obtain

Therefore

Substitution Equation (3.1) into Equation (3.33) gives

Let us calculate now integral (3.34) using Laplace’s approximation. It is easy to see that corresponding stationary point 

Substitution Equation (3.35) into inequality (3.13) gives the inequality (3.11). The inequality (3.11) completed the proof.
4. Quantum Anharmonic Oscillator with a Cubic Potential Supplemented by Additive Sinusoidal Driving
In this subsection we calculate exact quasi-classical asymptotic for quantum anharmonic oscillator with a cubic potential supplemented by additive sinusoidal driving. Using Theorem 3.1 we obtain corresponding limiting quantum trajectories given via Equation (1.3).
Let us consider quantum anharmonic oscillator with a cubic potential

Supplemented by an additive sinusoidal driving. Thus

The corresponding master Lagrangian given by (3.7), are

We assume now that: 

where 

The corresponding master action 

The linear system of the algebraic Equation (3.9) are

Therefore

The linear system of the algebraic Equation (3.10) are

Therefore the solution of the linear system of the algebraic Equation (3.10) are

Transcendental master Equation (3.11) are

Finally from Equation (4.10) one obtain

where
Numerical Examples
Example 1 (in Figure 1 and Figure 2).






5. Comparison Exact Quasi-Classical Asymptotic with Stationary-Point Approximation
We set now


Figure 1. Limiting quantum trajectory 
Figure 2. Limiting quantum trajectory 
Note that for corresponding propagator 


where 

Here the initial-



Let us calculate now integral (5.2) using stationary-point approximation. Denoting an critical points of the discrete-time action (5.3) by 


for



From Equation (5.2) in the limit 

Here the pre-factor 

The Gaussian integral in (5.6) is given via canonical formula

Here 


Let us consider now Cauchy problem (2.8) with initial data 

Note that for corresponding Colombeau solution 


Let us calculate now integrals in RHS of Equation (5.8) using stationary-point approximation. Corresponding critical point conditions are

From (5.8) we obtain


Let as denote 

Therefore the time discretized path-integral representation of the Colombeau quantum averages given by Equation (1.1) are
(5.13)
where




Here 

From Equations (5.13)-(5.14) one obtain

and
As demonstrated in [24] the determinant appearing in (5.11) can be calculated using second order linear recursion:

with initial data

from which the pre-factor

In the limit 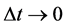

In the limit 

with initial data

By integration Equation (5.22) one obtain the first order linear differential equation

In the limit 

We set now in Equation (5.1)

Corresponding differential master equation are

From Equation (5.27) one obtain that corresponding transcend dental master equation are

Numerical Examples
Comparison of the: 1) classical dynamics calculated by using Equation (5.1) (red curve), 2) limiting quantum trajectory 
Figure 3. Limiting quantum trajectory 
Figure 4. Limiting quantum trajectory 
6. Conclusions
We pointed out that there existed limiting quantum trajectories given via Equation (1.3) with a jump. Such jump does not depend on any single measurement of particle position 

An axiom of quantum mechanics is that we cannot predict the result of any single measurement of an observable of a quantum mechanical system in a superposition of eigenstates. However we can predict the result of any single measurement of particle position 




Acknowledgements
A reviewer provided important clarification.
Cite this paper
Jaykov Foukzon,Alex Potapov,Stanislav Podosenov, (2015) Exact Quasi-Classical Asymptotic beyond Maslov Canonical Operator and Quantum Jumps Nature. Journal of Applied Mathematics and Physics,03,584-607. doi: 10.4236/jamp.2015.35072
References
- 1. Vijay, R., Slichter, D.H. and Siddiqi, I. (2011) Observation of Quantum Jumps in a Superconducting Artificial Atom. Physical Review Letters, 106, Article ID: 110502.
http://dx.doi.org/10.1103/PhysRevLett.106.110502 - 2. Peil, S. and Gabrielse, G. (1999) Observing the Quantum Limit of an Electron Cyclotron: QND Measurements of Quantum Jumps between Fock States. Physical Review Letters, 83, 1287-1290.
- 3. Sauter, T., Neuhauser, W., Blatt, R. and Toschek, P.E. (1986) Observation of Quantum Jumps. Physical Review Letters, 57, 1696-1698.
http://dx.doi.org/10.1103/PhysRevLett.57.1696 - 4. Bergquist, J.C., Hulet, R.G., Itano, W.M. and Wineland, D.J. (1986) Observation of Quantum Jumps in a Single Atom. Physical Review Letters, 57, 1699-1702.
http://dx.doi.org/10.1103/PhysRevLett.57.1699 - 5. Bohr, N. (1913) On the Constitution of Atoms and Molecules. Philosophical Magazine, 26, 1-25.
http://dx.doi.org/10.1080/14786441308634955 - 6. Dum, R., Zoller, P. and Ritsch, H. (1992) Monte Carlo Simulation of the Atomic Master Equation for Spontaneous Emission. Physical Review A, 45, 4879.
http://dx.doi.org/10.1103/PhysRevA.45.4879 - 7. Dalibard, J., Castin, Y. and Mølmer, K. (1992) Wave-Function Approach to Dissipative Processes in Quantum Optics. Physical Review Letters, 68, 580.
- 8. Gatarek, D. (1991) Continuous Quantum Jumps and Infinite-Dimensional Stochastic Equations. Journal of Mathematical Physics, 32, 2152-2157.
- 9. Molmer, K., Castin, Y. and Dalibard, J. (1993) Monte Carlo Wave-Function Method in Quantum Optics. Journal of the Optical Society of America B, 10, 524-538.
http://dx.doi.org/10.1364/JOSAB.10.000524 - 10. Gardiner, C.W., Parkins, A.S. and Zoller, P. (1992) Wave-Function Quantum Stochastic Differential Equations and Quantum-Jump Simulation Methods. Physical Review A, 46, 4363-4381.
- 11. Vogt, N., Jeske, J. and Cole, J.H. (2013) Stochastic Bloch-Redfield Theory: Quantum Jumps in a Solid-Stateenvironment. Physical Review B, 88, Article ID: 174514.
- 12. Reiner, J.E., Wiseman, H.M. and Mabuchi, H. (2003) Quantum Jumps between Dressed States: A Proposed Cavity-QED Test Using Feedback. Physical Review A, 67, Article ID: 042106.
http://dx.doi.org/10.1103/PhysRevA.67.042106 - 13. Berkeland, D.J., Raymondson, D.A. and Tassin, V.M. (2004) Tests for Non-Randomness in Quantum Jumps. Physical Review A, 69, Article ID: 052103.
- 14. Wiseman, H.M. and Milburn, G.J. (1993) Interpretation of Quantum Jump and Diffusion Processes Illustrated on the Bloch Sphere. Physical Review A, 47, 1652-1666.
http://dx.doi.org/10.1103/PhysRevA.47.1652 - 15. Wiseman, H.M. and Toombes, G.E. (1999) Quantum Jumps in a Two-Level Atom: Simple Theories versus Quantum Trajectories. Physical Review A, 60, 2474.
http://dx.doi.org/10.1103/PhysRevA.60.2474 - 16. Stojanovic, M. (2008) Regularization for Heat Kernel in Nonlinear Parabolic Equations. Taiwanese Journal of Mathematics, 12, 63-87.
http://www.tjm.nsysu.edu.tw/ - 17. Garetto, C. (2008) Fundamental Solutions in the Colombeau Framework: Applications to Solvability and Regularity Theory. Acta Applicandae Mathematicae, 102, 281-318.
http://dx.doi.org/10.1007/s10440-008-9220-8 - 18. Foukzon, J., Potapov, A.A. and Podosenov, S.A. (2011) Exact Quasiclassical Asymptotics beyond Maslov Canonical Operator. International Journal of Recent advances in Physics, 3.
http://arxiv.org/abs/1110.0098 - 19. Feynman, E.N. (1964) Integrals and the Schrodinger Equation. Journal of Mathematical Physics, 5, 332-343.
http://dx.doi.org/10.1063/1.1704124 - 20. Maslov, V.P. (1976) Complex Markov Cheins and Continual Feynman Integral. Nauka, Moskov.
- 21. Apostol, T.M. (1974) Mathematical Analysis. 2nd Edition, Addison-Wesley, Boston.
- 22. Chen, W.W.L. (2003) Fundamentals of Analysis. Published by Chen, W.W.L. via Internet.
- 23. Gupta, S.L. and Rani, N. (1998) Principles of Real Analysis. Vikas Puplishing House, New Delhi.
- 24. Lehmann, J., Reimann, P. and Hanggi, P. (2000) Surmounting Oscillating Barriers: Path-Integral Approach for Weak Noise. Physical Review E, 62, 6282.
http://dx.doi.org/10.1103/PhysRevE.62.6282 - 25. Fedoryuk, M.V. (1977) The Method of Steepest Descent. Moscow. (In Russian)
- 26. Fedoryuk, M.V. (1989) Asymptotic Methods in Analysis. Encyclopaedia of Mathematical Sciences, 13, 83-191.
http://dx.doi.org/10.1007/978-3-642-61310-4_2 - 27. Shun, Z. and McCullagh, P. (1995) Laplace Approximation of High Dimensional Integrals. Journal of the Royal Statistical Society: Series B (Methodological), 57, 749-760.
- 28. Foukzon, J. (2014) Strong Large Deviations Principles of Non-Freidlin-Wentzell Type-Optimal Control Problem with Imperfect Information—Jumps Phenomena in Financial Markets. Communications in Applied Sciences, 2, 230-363.
Appendix
Let us consider now regularized Feynman-Colombeau propagator 

where








Here:1)







3) 
Therefore regularized Colombeau solution of the Schrödinger equation corresponding to regularized propagator (A.1) are

Here
Let us consider now regularized quantum average

From (A.5) and (A.12) one obtain

From Equations (A.5)-(A.13) one obtain

Using replacement


Here

And


Let us rewrite a function 



where



Let use valuate now path integral 

(A.22.a)

(A.22.b)
where


(A.25.a)
(A.25.b)
(A.26.a)
(A.26.b)
Let us evaluate now n-dimensional path integral
(A.27)
From Equation (A.27) one obtain the inequality

From In Equation (A.28) one obtain the inequality

where


Using replacement


(A.32)






From (A.29)-(A.35) one obtain


Proposition A.1. [27] [28] Let


Then the iterated limit:



Proposition A.2. Let

uation (A.25) and let

tion (A.26). Then
1)
2)
3)
4)
5)
6)
Here


Proof (I) Let us to choose an sequence 
1) 
2)
We note that from (ii) follows that: perturbative expansion
vanishes in the limit

Let us to choose now an subsequence 
exist and
From (A.39) and Proposition A.1 one obtain

From (A.39), (A.40) and (A.38) one obtain

The inequality (A.41) completed the proof of the statement (1).
(II) Let us estimate now n-dimensional path integral

From Equation (A.42) one obtain the inequality

where

Using replacement


(A.45)






From (A.43)-(A.48) one obtain

Let us to choose an sequence 
1) 
2)
We note that from 2) follows that: perturbative expansion

Vanishes in the limit

Let us to choose now an subsequence 
exist and 
From (A.51) and Proposition A.1 one obtain

From (A.50), (A.51) and (A.52) one obtain
Proof of the statements (3)-(6) is similarly to the proof of the statements (1)-(2).
Theorem A.1. Let

where 


Here


Proof. We remain that

From Equation (A.56) we obtain

Let us to choose now an sequences


1)
2)
3)
Therefore from inequality (A.57), Equation (A.58) and inequality (A.59) we obtain





















