Journal of Modern Physics
Vol.05 No.17(2014), Article ID:51908,5 pages
10.4236/jmp.2014.517192
Investigation of the Temperature Dependence of the Oscillation of the Magnetic Susceptibility in Semiconductors
G. Gulyamov1, U. I. Erkaboev1, N. Yu. Sharibaev1,2
1Namangan Engineering-Pedagogical Institute, Namangan, Uzbekistan
2Namangan Engineering-Technology Institute, Namangan, Uzbekistan
Email: Gulyamov1949@mail.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 September 2014; revised 26 September 2014; accepted 15 October 2014
ABSTRACT
The temperature dependence of the magnetic susceptibility oscillations semiconductors was con- sidered in a quantizing magnetic field. With the help of mathematical modeling of the thermal broadening of the energy levels, the temperature dependence of the de Haas-van Alphen effect in quantizing magnetic field was investigated. The influence of temperature on the de Haas-van Alphen with the help of free energy of electrons 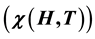 in semiconductors was determined. Theoretical results of the mathematical simulation were compared with experimental data for bismuth. Using the proposed model of the low-temperature
in semiconductors was determined. Theoretical results of the mathematical simulation were compared with experimental data for bismuth. Using the proposed model of the low-temperature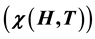 , high-temperature oscillation magnetic susceptibility in semiconductors was calculated.
, high-temperature oscillation magnetic susceptibility in semiconductors was calculated.
Keywords:
Density of States, The Energy Spectrum, The Numerical Simulation and Experiment

1. Introduction
In a strong magnetic field, the energy spectrum of electrons in a semiconductor becomes quantized, so that the density of states as a function of energy acquires an oscillating character. This circumstance is the root cause of occurrence of oscillatory magnetic field dependence of a number of equilibrium and nonequilibrium quantities characterizing the state and behavior of the electrons in the crystal in a quantizing magnetic field. Currently, these oscillations are united under the general name of quantum oscillation effects [1] .
Effect de Haas-van Alphen (dHvA) is a versatile and powerful tool to study the energy spectrum of the free electron systems in semiconductors. The first time the definition of the oscillations of the magnetic susceptibility was observed experimentally in bismuth crystals at low temperatures and strong magnetic fields [2] .
dHvA effect in recent years due to intensive research of low-dimensional structures, primarily of semiconductor nanostructures in which the spectrum of the Landau levels is determined primarily positions dimensional quantization levels. [3] [4] detected dHvA oscillations at high temperatures and weak magnetic fields using measurements of the field and temperature dependences of the static magnetic susceptibility of nanoscale semiconductors.
Work [5] - [12] considered that the temperature dependence of the density of states is determined by relaxation spectroscopy of the energy levels in semiconductors. It has been shown that the density of surface states is temperature-dependent―a method of determining the density of surface states. It has been shown that due to the energy levels of thermal broadening, a discrete spectrum with a rise in temperature is transformed into a continuous energy spectrum. With the expansion of the energy spectrum of the density of states function GN has been shown that the value of the energy gap will depend on the temperature. These studies do not consider the properties of the magnetic oscillation effects in semiconductors.
The aim of this work is to study the temperature dependence of the magnetic susceptibility and the comparison of theoretical calculations with experimental results.
2. Influence of Temperature on the Magnetic Susceptibility in Semiconductors
Consider the free energy of the electron gas. According, the Gibbs distribution can be written as [13] [14]
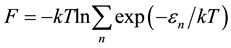 (1)
(1)
where,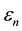 ―energy levels of the system.
―energy levels of the system.
The free energy F is expressed in terms of electron density of states Ns. The free energy of an electron in a quantizing magnetic field is determined by the following formula [15] :
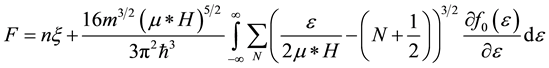 (2)
(2)
where,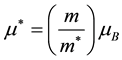 ―“effective” Bohr magneton,
―“effective” Bohr magneton,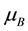 ―Bohr magneton, H―magnetic field strength, N― number of Landau levels,
―Bohr magneton, H―magnetic field strength, N― number of Landau levels,
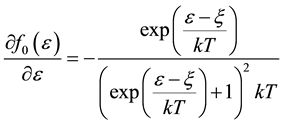 (3)
(3)
Second-order derivative of 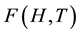 in the magnetic field strength, the magnetic susceptibility has
in the magnetic field strength, the magnetic susceptibility has
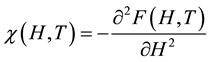 (4)
(4)
The occurrence of oscillations of the magnetic susceptibility 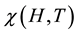 can be explained qualitatively as follows.
can be explained qualitatively as follows.
Figure 1 shows graphs of the oscillations of the magnetic susceptibility calculated by Formulas (2)-(4) in a
strong magnetic field at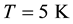 ,
,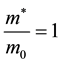 . At such low temperatures, the influence of the thermal broadening
. At such low temperatures, the influence of the thermal broadening
of the weak. Figure 1 shows that with increasing magnetic field strength, the oscillation amplitude of the magnetic susceptibility 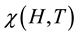 increases.
increases.
Figure 2 shows the oscillations of the magnetic susceptibility for different temperatures. As can be seen from these figures, at a temperature of  peaks effect dHvA oscillations due to Landau quantization is do not observed.
peaks effect dHvA oscillations due to Landau quantization is do not observed.
In work [10] to determine the probability devastation energy states showed that, if 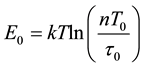 the
the
Figure 1. Dependence of the oscillation of the magnetic susceptibility of the strength magnetic field.
Figure 2. Change in the magnetic susceptibility at different temperatures in strong magnetic fields, calculated by Formulas (3) and (4).
function of probability devastation energy states is 

at low temperatures describes―the Dirac delta function.
Function of the form 
From here follow, the function, 

is a delta-Dirac function. It is well known that the derivative of the energy function is the Fermi-Dirac Dirac 
Thus, to study the temperature dependence of the magnetic susceptibility of the oscillations in the Formula (2) 
Then we can calculate the temperature dependence of magnetic susceptibility of the oscillation with the aid of Formulas (2), (4) and (5).
3. Comparison of Theoretical Calculations with Experimental Results
In the work [2] experiments were conducted on bismuth in stronger magnetic fields and low temperatures. Initial data for the application of formulas (4) and (5) is an experimental oscillation of magnetic susceptibility at a particular temperature T (temperature experiment). Figure 3(a) shows the oscillation of the magnetic susceptibility at

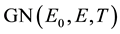


Figure 3. Changing the oscillations of magnetic susceptibility in a strong quan- tizing magnetic field. (a) Experiment [2] and the model calculation for bismuth at
susceptibility of bismuth observed at the temperature of the experiment. Because, in this experiment

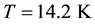


ruptly. With increasing temperature starts to smooth sharp spikes and at sufficiently high temperatures


4. Conclusion
The dependence of the oscillation of the magnetic susceptibility of the temperature in a quantizing magnetic field by the free energy of the electrons was investigated. It is shown that, as temperature is increased starts to smooth sharp spikes and at sufficiently high temperatures 

References
- Tsidilkovsky, I.M. (1972) Electrons and Holes in Semiconductors. Nauka, Moscow, Chapter 6, 526.
- Schoenberg, D. (1986) Magnetic Oscillations in Metals. Wiley, New York, Chapter 1, 25.
- Bagraev, N.T., Brilinskaya, E.S., Gets, D.S., Klyachkin, L.E., Malyarenko, A.M. and Novels, V.V. (2011) Fizika i Tekhnika Poluprovodnikov, 45, 1503-1508.
- Bagraev, N.T., Brilinskaya, E.S., Danilovsky, E.Yu., Klyachkin, L.E., Malyarenko, A.M. and Romanov, V.V. (2012) Fizika i Tekhnika Poluprovodnikov, 46, 90-95.
- Gulyamov, G. and Sharibaev, N.Yu. (2011) Fizika i Tekhnika Poluprovodnikov, 45, 178-182.
- Gulyamov, G., Sharibaev, N.Yu. and Erkaboev, U.I. (2012) Fyzicheckaya Injeneriya Poverkhnosti, 10, 366-370.
- Gulyamov, G., Karimov, I.N., Sharibaev, N.Yu. and Erkaboev, U.I. (2010) Uzbek Journal of Physics, 12, 143-146.
- Gulyamov, G., Sharibaev N.Y. and Erkaboev, U.I. (2013) World Journal of Condensed Matter Physics, 3, 216-220. http://dx.doi.org/10.4236/wjcmp.2013.34036
- Gulyamov, G., Erkaboev, U.I. and Sharibaev, N.Y. (2013) Physical Surface Engineering, 11, 289-292.
- Gulyamov, G., Erkaboev, U.I. and Sharibaev, N.Y. (2014) Journal of Modern Physics, 5, 680-685. http://dx.doi.org/10.4236/jmp.2014.58079
- Gulyamov, G., Erkabaev, U.I. and Sharibaev, N.Yu. (2014) Semiconductors, 48, 1287-1292.
- Gulyamov, G., Sharibaev, N.Y. and Erkaboev, U.I. (2014) Fyzicheckaya Injeneriya Poverkhnosti, 11, 9-13.
- Landau, L.D. and Lifshitz, E.M. (1976) Statistical Physics. Nauka, Moscow, Part 1, Chapter 3, 109.
- Abrikosov, A.A. (1987) Fundamentals of the Theory of Metals. Nauka, Moscow, Chapter 10, 156.
- Anselm, A.I. (1978) Introduction to the Theory of Semiconductors. Nauka, Moscow, Chapter 6, 367.






