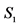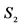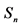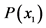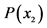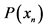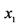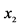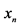Natural Science
Vol.6 No.7(2014), Article
ID:45366,13
pages
DOI:10.4236/ns.2014.67055
Entropy—A Universal Concept in Sciences
Vladimír Majerník
Mathematical Institute, Slovak Academy of Sciences, Bratislava, Slovakia
Email: Eva.Majernikova@savba.sk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 February 2014; revised 24 March 2014; accepted 31 March 2014
ABSTRACT
Entropy represents a universal concept in science suitable for quantifying the uncertainty of a series of random events. We define and describe this notion in an appropriate manner for physicists. We start with a brief recapitulation of the basic concept of the theory probability being useful for the determination of the concept of entropy. The history of how this concept came into its to-day exact form is sketched. We show that the Shannon entropy represents the most adequate measure of the probabilistic uncertainty of a random object. Though the notion of entropy has been introduced in classical thermodynamics as a thermodynamic state variable it relies on concepts studied in the theory of probability and mathematical statistics. We point out that whole formalisms of statistical mechanics can be rewritten in terms of Shannon entropy. The notion “entropy” is differently understood in various science disciplines: in classical physics it represents the thermodynamical state variable; in communication theory it represents the efficiency of transmission of communication; in the theory of general systems the magnitude of the configurational order; in ecology the measure for bio-diversity; in statistics the degree of disorder, etc. All these notions can be mapped on the general mathematical concept of entropy. By means of entropy, the configurational order of complex systems can be exactly quantified. Besides the Shannon entropy, there exists a class of Shannon-like entropies which converge, under certain circumstances, toward Shannon entropy. The Shannon-like entropy is sometimes easier to handle mathematically then Shannon entropy. One of the important Shannon-like entropy is well-known Tsallis entropy. The application of the Shannon and Shannon-like entropies in science is really versatile. Besides the mentioned statistical physics, they play a fundamental role in the quantum information, communication theory, in the description of disorder, etc.
Keywords:Probability, Uncertainty, Shannon Entropy, Shannon-Like Entropies

1. Introduction
At the most fundamental level, all our further considerations rely on the concept of probability. Although there is a well-defined mathematical theory of probability, there is no universal agreement about the meaning of probability. Thus, for example, there is the view that probability is an objective property of a system and another view that it describes a subjective state of belief of a person. Then there is the frequentist view that the probability of an event is the relative frequency of its occurrence in a long or infinite sequence of trials. This latter interpretation is often employed in the mathematical statistics and statistical physics. The probability means in everyday life the degree of ignorance about the outcome of a random trial. This is why the probability is commonly interpreted as degree of the subjective expectation of an outcome of a random trial. Both subjective and statistical probability are “normed”. It means that the degree of expectation that an outcome of a random trial occurs, and the degree of the “complementary” expectation, that it does not, is always equal to one [1] 1.
Although the concept of probability is here covered in a sophisticated mathematical language, it expresses only the commonly familiar properties of probability used in everyday life. For example, each number of spots at the throw of a simple die represents an elementary random event to which a positive real number is associated called its probability (relation (i)). The probability of two (or more) numbers of spots at the throw of a simple die is equal to the sum of their probabilities (relation (iii)). The sum of probabilities of all possible numbers of spots is normed to one (relation (iv)).
The word “entropy”2 was first used in 1984 by Clausius in his book Abhandlungen über Wärmetheorie to describe a quantity accompanying a change from the thermal to mechanical energy and it continued to have this meaning in thermodynamics. Boltzmann [2] in his Vorlesungen über Gastheorie presented the statistical interpretation of the thermodynamical entropy. He linked the thermodynamic entropy with the molecular disorder. The general concept of entropy as a measure of uncertainty was first introduced by Shannon and Wiener. Shannon is also credited for the development of a quantitative measure of the amount of information [3] . Shannon entropy may be considered as a generalization of entropy, defined by Hartley, when the probability of each event is equal. Nyquist [4] was the first author who introduced a measure of information. His paper has largely remained unnoticed. After publication of Shannon seminal paper in 1948 [3] , the use of entropy as measure of uncertainty grew rapidly and was applied with various successes in most area of human endeavor.
Mathematicians were attracted to the possibility of providing axiomatic structure of entropy and to the ramification thereof. The axiomatic approach to the concept of entropy attempts to find a system of postulates which provides a unique mathematical characteristic of entropy3 and which adequately reflects the properties asked from the probabilistic uncertainty measure in a diversified real situation. This has been very interesting and thought-provoking area for scientists. Khinchin [5] was the first who gave a clear and rigorous presentation of the mathematical foundation of entropy. A good number of works have been done to describe the properties of entropy. An extensive list of works in this field can be found in the book of Aczcél and Daróczy [6] .
The fundamental concept for the description of random processes is the notion of the random trial. A random trial is characterized by a set of its outcomes (values) and the corresponding probability distribution. A typical random trial is the throw of a single dice characterized by the following scheme (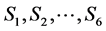 are the positions of dice after its throwing)
are the positions of dice after its throwing)
| S | S1 | S2 | S3 | S4 | S5 | S6 |
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| x | 1 | 2 | 3 | 4 | 5 | 6 |
To any random trial it is assigned a random variable 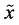 which represents a mathematical quantity assuming a set of values with the corresponding probabilities (see, e.g. [1] ).
which represents a mathematical quantity assuming a set of values with the corresponding probabilities (see, e.g. [1] ).
There are two measures which express the uncertainty of a random trial:
(i) The moment measures containing in its definition both the values assigned to trial outcomes and the set of the corresponding probabilities. The moment uncertainty measures are given as a rule by the higher statistical moments of a random variable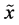 . As it is well-known, the
. As it is well-known, the 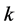 -th moment about zero (uncorrelated moment)
-th moment about zero (uncorrelated moment)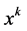 , and the central moment of the
, and the central moment of the 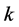 -th order
-th order 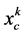 assigned to a discrete random variable
assigned to a discrete random variable 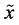 with the probability distribution
with the probability distribution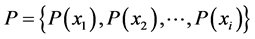 , is defined as
, is defined as
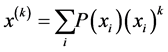
and
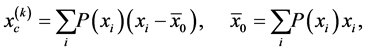
respectively.
The statistical moments of a random variable are often used as the uncertainty measures of the random trial, especially in the experimental physics, where, e.g., the standard deviation of measured quantities characterizes the accuracy of a physical measurement. The moment uncertainty measures of a random variable are also used by formulating the uncertainty relations in quantum mechanics [7] .
(ii) The probabilistic or entropic measures of uncertainty of a random trial contain in their expressions only the components of the probability distribution of a random trial.
To determine the notion of entropy we consider quantities, called as partial uncertainties which are assigned to individual probabilities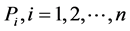 . A partial uncertainty we denote by symbol
. A partial uncertainty we denote by symbol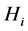 . In any probabilistic uncertainty measures, a partial uncertainty is function only of the corresponding probability
. In any probabilistic uncertainty measures, a partial uncertainty is function only of the corresponding probability 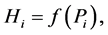
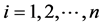 . The requirements asked from a partial uncertainty
. The requirements asked from a partial uncertainty 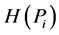 are the following [8] : (see Appendix):
are the following [8] : (see Appendix):
(i) It is a monotonously decreasing continuous and unique function of the corresponding probability;
(ii) The common value of the uncertainty of a certain outcome of two statistically independent trials 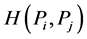 is additive, i.e.
is additive, i.e.
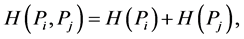 (1)
(1)
where 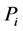 and
and 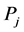 are the probability of the i-th and j-th outcome, respectively;
are the probability of the i-th and j-th outcome, respectively;
(iii)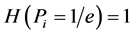 .
.
It was shown that the only function which satisfies these requirements has the form [8]
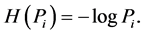
The mean value of the partial uncertainties  is
is
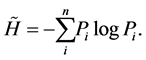 (2)
(2)
The quantity 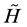 is called information-theoretical or Shannon entropy. We denote it by symbol S. Shannon entropy is a real and positive number. It is a function only of the components of the probability distribution
is called information-theoretical or Shannon entropy. We denote it by symbol S. Shannon entropy is a real and positive number. It is a function only of the components of the probability distribution 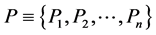 assigned to the set of outcomes of a random trial.
assigned to the set of outcomes of a random trial.
Shannon entropy satisfies the following demands (see Appendix): (i) If the probability distribution contains only one component, e.g.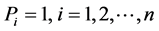 , and the rest components are equal to zero, then
, and the rest components are equal to zero, then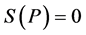 . In this case, there is no uncertainty in a random trial because an outcome is realized with certainty.
. In this case, there is no uncertainty in a random trial because an outcome is realized with certainty.
(ii) The more spread is the probability distribution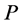 , the larger becomes the entropy
, the larger becomes the entropy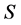 .
.
(iii) For a uniform probability distribution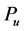 ,
, 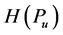 becomes maximal. In this case, the probabilities of all outcomes are equal, therefore the mean uncertainty of such a random trial becomes maximum.
becomes maximal. In this case, the probabilities of all outcomes are equal, therefore the mean uncertainty of such a random trial becomes maximum.
One uses for the characterization of a random trial a random scheme. If 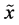 is a discrete random variable assigned to a random trial then its random scheme has the form
is a discrete random variable assigned to a random trial then its random scheme has the form
| S |
|
|
|
| P |
|
|
|
| X |
|
|
|
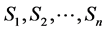 are the outcomes of a random trial (in quantum physics, e.g. the quantum states),
are the outcomes of a random trial (in quantum physics, e.g. the quantum states), 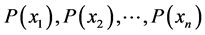 are their probabilities and
are their probabilities and 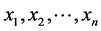 are the values defined on
are the values defined on 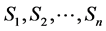 (in quantum physics, e.g. the eigenvalues). A probability distribution,
(in quantum physics, e.g. the eigenvalues). A probability distribution, 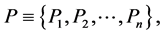 is the complete set of probabilities of all individual outcomes of a random trial.
is the complete set of probabilities of all individual outcomes of a random trial.
We note that there is a set of the probabilistic uncertainty measures defined by means of other functions then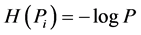 . They are called nonstandard or Shannon-like entropies. We shall deal with them in the next sections.
. They are called nonstandard or Shannon-like entropies. We shall deal with them in the next sections.
2. Entropy as a Qualificator of the Configurational Order
Since the simple rule holds that the smaller the order in a system the larger its entropy, the entropy appears to be the appropriate quantity for the expression of the measure of the configurational order (organization). The orderliness and entropy of a physical system are related to each other inversely so that any increase in the degree of configurational order must necessarily result in the decrease of its entropy. The measure of the configurational order constructed by using entropies is called Watanabe measure and is defined as follows [9] :
configurational order of a system = (sum of entropies of the parts of the system) − (entropy of the whole system).
The Watanabe measure for configurational order is related to the other measure of configurational organization well-known in theory of information, called redundancy. Both measures express quantitatively the property of the configurationally organized systems to have order between its elements, which causes that the system as a whole behaves in a more deterministic way than its individual parts. If a system consists only of elements which are statistically independent, the Watanabe measure for the configurational organization becomes zero. If the elements of a system are deterministically dependent, its configurational organization gets the maximum value. A general system has its configurational organization between these extreme values. To the prominent systems which can be organized configurationally belong physical statistical systems (i.e., about all, Ising systems of spins) [10] . High configurational organization is exhibited especially by systems which have some spatial, temporal or spatio-temporal structures that have arisen in a process which takes place far from thermal equilibrium (e.g. laser, fluid instabilities, etc.) [11] . These systems can be sustained only by a steady flow of energy and matter, therefore they are called open systems [12] . A large class of systems, which are generally organized configurationally as well as functionally, comprises the so-called string systems which represent sequences of elements forming finite alphabets. To these systems belong, e.g., language, music, genetic DNA and various bio-polymers. Since many of such systems are goal-directed and have a functional organization as well, they are especially appropriate for the study of the interrelation between the configurational and functional organization [10] .
3. The Concept of Entropy in Thermodynamics and Statistical Physics
A remarkable event in the history of physics was the interpretation of the phenomenological thermodynamics in terms of motion and randomness. In this interpretation, the temperature is related to motion while the randomness is linked with the Clausius entropy. The homeomorphous mapping of the phenomenological thermodynamics on the formalism of mathematical statistics gave rise to two entropy concepts: the Clausius thermodynamic entropy as a thermodynamic state variable of a thermodynamic system and the Boltzmann statistical entropy as the logarithm of probability of state of a physical ensemble. The fact that the thermodynamic entropy is a state variable means that it is completely defined when the state (pressure, volume, temperature, etc.) of a thermodynamic system is defined. This is derived from mathematics, which shows that only the initial and final states of a thermodynamic system determine the change of its entropy. The larger the value of the entropy of a particular state of a thermodynamic system, the less available is the energy of this system to do work.
The statistical concept of entropy was introduced in physics when seeking a statistical quantity homeomorphous with the thermodynamic entropy. As it is well-known, the Clausius entropy of a thermodynamic system 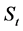 is linked with ensemble probability
is linked with ensemble probability 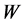 by the celebrated Boltzmann law,
by the celebrated Boltzmann law, 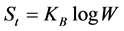 , where
, where 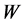 is so-called “thermodynamic” probability determined by the configurational properties of a statistical system and
is so-called “thermodynamic” probability determined by the configurational properties of a statistical system and 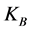 is the Boltzmann constant4. The Boltzmann law represents the solution to the functional equation between
is the Boltzmann constant4. The Boltzmann law represents the solution to the functional equation between 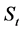 and
and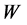 . Let us consider a set of the isolated thermodynamic systems
. Let us consider a set of the isolated thermodynamic systems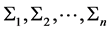 . According to Clausius, the total entropy of this system is an additive function of the entropies of its parts, i.e., it holds
. According to Clausius, the total entropy of this system is an additive function of the entropies of its parts, i.e., it holds
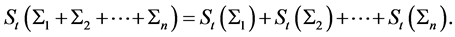 (3)
(3)
On the other side, the joint “thermodynamic” probability of system (3) is
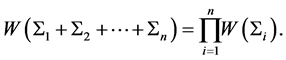 (4)
(4)
To obtain the homomorphism between Equations (3) and (4), it is sufficient that
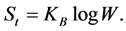 (5)
(5)
which is just the Boltzmann law [2] .
We give some remarks regarding the relationship between the Clausius, Boltzmann and Shannon entropies:
(i) The thermodynamic probability 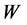 in the Boltzmann law is given by the number of the possibilities how to distribute
in the Boltzmann law is given by the number of the possibilities how to distribute 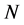 particles in
particles in 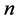 cells having different energies
cells having different energies 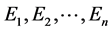
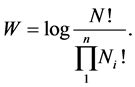
We show that the physical entropy given by Boltzmann’s law is equal to the sum of Shannon entropies of energies taken as random variables defined on the individual particles, i.e.,
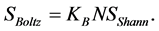 (6)
(6)
The probability 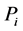 that a particle of the statistical ensemble has the i-th value of energy is given by the ratio
that a particle of the statistical ensemble has the i-th value of energy is given by the ratio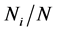 . Inserting the probabilities
. Inserting the probabilities
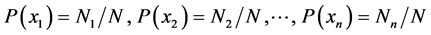 (7)
(7)
into Boltzmann’s entropy formula we have
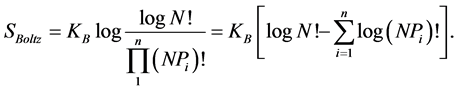 (8)
(8)
Supposing that the number of particles in a statistical ensemble is very large, we can use the asymptotic formula
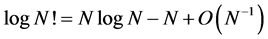
which inserted in Boltzmann’s entropy yields
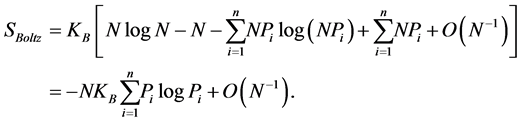 (9)
(9)
For very large N, the second term in Equation (9) can be neglected and we find
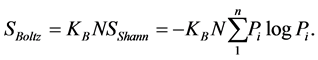
We see that the Boltzmann entropy of an ensemble with large 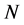 is equal to the sum of Shannon entropies of the individual particles. The asymptotical equality between Boltzmann and Shannon entropies for the large
is equal to the sum of Shannon entropies of the individual particles. The asymptotical equality between Boltzmann and Shannon entropies for the large 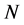 makes it possible to use the Shannon entropy also for describing an statistical ensemble. The pioneer on this field was E. Jaynes who published, already in fifties, works in which only Shannon entropy was used to formulate statistical physics [13] . However, many authors advocating the use of Shannon entropy in statistical physics do not fully realized the difference between Boltzmann’s and Shannon entropy. The use of Shannon entropy can be only justified if one considers the physical ensemble as a system of random objects on which energy (or other physical quantity) is taken as a random variable. Then, the total entropy of the whole ensemble is given as the sum of Shannon entropies of individual statistical elements (e.g., particles). While the Boltzmann’s entropy loses its sense for an ensemble containing only a few particles, Shannon entropy is defined also for an “ensemble” with even one particle. Boltzmann’s entropy is typical ensemble concept while Shannon entropy is a probabilistic concept. This is not only the change of the methodology when treating statistical ensemble but it has also long-reaching conceptual and even pedagogical consequences.
makes it possible to use the Shannon entropy also for describing an statistical ensemble. The pioneer on this field was E. Jaynes who published, already in fifties, works in which only Shannon entropy was used to formulate statistical physics [13] . However, many authors advocating the use of Shannon entropy in statistical physics do not fully realized the difference between Boltzmann’s and Shannon entropy. The use of Shannon entropy can be only justified if one considers the physical ensemble as a system of random objects on which energy (or other physical quantity) is taken as a random variable. Then, the total entropy of the whole ensemble is given as the sum of Shannon entropies of individual statistical elements (e.g., particles). While the Boltzmann’s entropy loses its sense for an ensemble containing only a few particles, Shannon entropy is defined also for an “ensemble” with even one particle. Boltzmann’s entropy is typical ensemble concept while Shannon entropy is a probabilistic concept. This is not only the change of the methodology when treating statistical ensemble but it has also long-reaching conceptual and even pedagogical consequences.
According to Jaynes [14] , the equilibrium probability distribution of the particle energy of a statistical ensemble should maximize the Shannon entropy
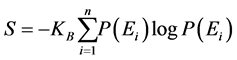 (10)
(10)
subject to given constraints. For example, by taking the mean energy per particle as the constraint at the extremizing procedure, we obtain the following probability distribution for the particle energy
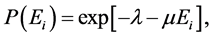
where the constants 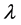 and
and 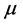 are to be determined by substituting
are to be determined by substituting 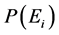 into constraint’s equations. We see how easily and quickly we obtain results forming the essence of the classical statistical mechanics. The use of Shannon entropy in statistical physics makes it possible to rewrite it in terms of modern theory of probability where a statistical ensemble is treated as a collection of the mutually interacting random objects [13] .
into constraint’s equations. We see how easily and quickly we obtain results forming the essence of the classical statistical mechanics. The use of Shannon entropy in statistical physics makes it possible to rewrite it in terms of modern theory of probability where a statistical ensemble is treated as a collection of the mutually interacting random objects [13] .
4. The Shannon-Like Entropies
Recently, there is an endeavour in the applied sciences (see, e.g. [15] ) to employ entropic measures of uncertainty having similar properties as information entropy, but they are simpler to handle mathematically. The classical measure of probabilistic uncertainty which has dominated in the literature since it was proposed by Shannon, is the information or Shannon entropy defined for a discrete random variable according by the formula
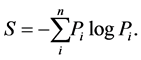 (11)
(11)
Since Shannon has introduced his entropy, several other classes of probabilistic uncertainty measures (entropies) have been described in the literature (see, e.g., [16] ). We can broadly divide them into two classes:
(i) The Shannon-like uncertainty measures which for a certain value of the corresponding parameters converge towards the Shannon entropy, e.g., Rényi’s entropy
(ii) The Maassen and Uffink uncertainty measures which converges also, under certain conditions, to the Shannon entropy,
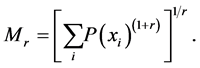 (12)
(12)
(iii) The uncertainty measures having no direct connection to Shannon entropy, e.g., information “energy” defined in information theory as [16]
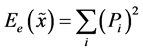 (13)
(13)
and called Hilbert-Schmidt norm in quantum physics. The most important uncertainty measures of the first class are:
(i) The Rényi entropy defined as follows [17]
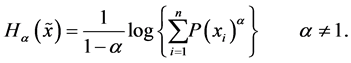 (14)
(14)
(ii) The Havrda-Charvat entropy (or 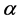 -entropy)5 is defined as [18]
-entropy)5 is defined as [18]
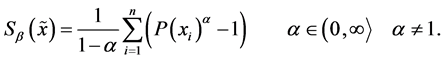 (15)
(15)
For the sake of completeness, we list some other entropy-like uncertainty measures presented in the literature [19] :
(i) The trigonometric entropy is defined as [10]
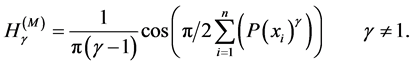 (16)
(16)
(ii) The R-norm entropy 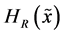 defined by the formula
defined by the formula
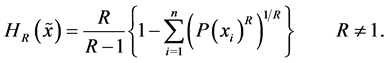
All the above-listed Shannon-like entropies converge towards Shannon entropy if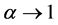 ,
, 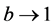 ,
,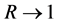 .
. 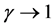 and
and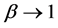 . In some instances, it is simpler to compute
. In some instances, it is simpler to compute 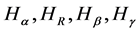 and
and 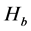 and then recover by taking limits
and then recover by taking limits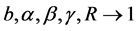 .
.
A quick inspection shows that all five Shannon-like entropies listed above are all mutually functionally related. For example, each of the Havrda-Charvat entropies can be expressed as a function of the Rényi’s entropy, and vice versa
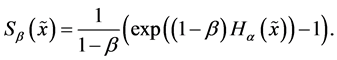
There are six properties which are usually considered desirable for a measure of a random trial: (i) symmetry, (ii) expansibility, (iii) subadditivity, (iv) additivity, (v) normalization, and (vi) continuity. The only uncertainty measure which satisfies all these requirements is Shannon entropy. Each of the other entropies violates at least one of them, e.g. Rényi’s entropy violates only the subadditivity property, Havrda-Charvat’s entropy violates the additivity property, the R-norm entropies violate both subadditivity and additivity. More details about the properties of each entropies can be found elsewhere (e.g., [15] ). The Shannon entropy satisfies all above requirements put on uncertainty measure and it exact matches the properties of physical entropy6. All these classes of entropies represent the probabilistic uncertainty measures which have similar mathematical properties as Shannon entropy.
The best known Shannon-like probabilistic uncertainty measure is the Havrda and Charvat entropy [18] which is more general than Shannon measure and much simpler than Renyi’s measure. It depends on a parameter 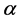 which is from the interval
which is from the interval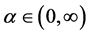 . As such, it represents a family of uncertainty measures which includes information entropy as a limiting case when
. As such, it represents a family of uncertainty measures which includes information entropy as a limiting case when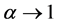 . We note that in physics the Havrda Charvat entropy is known as Tsallis entropy [20] . All the mentioned entropic measures of uncertainty are functions of the components of the probability distribution of a random variable
. We note that in physics the Havrda Charvat entropy is known as Tsallis entropy [20] . All the mentioned entropic measures of uncertainty are functions of the components of the probability distribution of a random variable 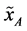 and they have three important properties: (i) They assume their maximal values for the uniform probability distribution of
and they have three important properties: (i) They assume their maximal values for the uniform probability distribution of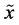 . (ii) They become zero for the probability distributions having only one component. (iii) They express a measure of the spread of a probability distribution. The larger this spread becomes, the smaller values they assume. These properties qualify them for being the measures of uncertainty (inaccuracy) in the physical theory of measurement.
. (ii) They become zero for the probability distributions having only one component. (iii) They express a measure of the spread of a probability distribution. The larger this spread becomes, the smaller values they assume. These properties qualify them for being the measures of uncertainty (inaccuracy) in the physical theory of measurement.
The entropic uncertainty measures for a discrete random variable are, in the frame of theory of probability, exactly defined. The transition from the discrete to the continuous entropic uncertainty measures is, however, not always unique and has still many open problems. A continuous random variable 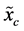 is characterized by the function of its probability density
is characterized by the function of its probability density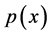 . The moment and probabilistic uncertainty measures exist also for the continuous random variables. The typical moment measure is the
. The moment and probabilistic uncertainty measures exist also for the continuous random variables. The typical moment measure is the 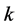 -th central moment of
-th central moment of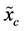 . The classical probabilistic uncertainty measure of a continuous random variable
. The classical probabilistic uncertainty measure of a continuous random variable 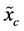 is the corresponding Shannon entropy
is the corresponding Shannon entropy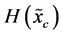 . It is a function of the probability density
. It is a function of the probability density 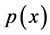 and consists of two terms7
and consists of two terms7
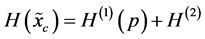
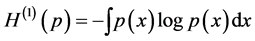
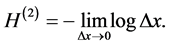
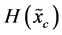 with both terms
with both terms 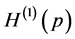 and
and 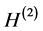 always diverges. Usually, one “renormalizes”
always diverges. Usually, one “renormalizes” 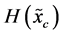 by taking only the term
by taking only the term 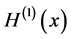 (called differential entropy or the Shannon entropy functional
(called differential entropy or the Shannon entropy functional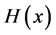 ) for the entropic uncertainty measure of a continuous random variable. This functional is well known to play an important role in probability and statistics. We refer to [15] for applications of the Shannon entropy functional to the theory of probability and statistics.
) for the entropic uncertainty measure of a continuous random variable. This functional is well known to play an important role in probability and statistics. We refer to [15] for applications of the Shannon entropy functional to the theory of probability and statistics.
As it is well-known, the Shannon entropy functionals of some continuous variables represent complicated integrals which often are difficult to compute analytically or even numerically. Everybody, who tried to calculate analytically the differential entropies of the continuous variables, became aware how difficult it may be. From the purely mathematical point of view, the differential entropy can be taken as a formula for expressing the spread of any standard single-valued function (the probability density belongs to this class of functions). Generally, the Shannon entropy functional assigns to a probability density function (belonging to the class of functions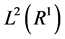 ) a real number
) a real number 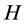 through a mapping
through a mapping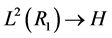 .
. 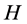 is a monotonously increasing function of the degree of “spreading” of
is a monotonously increasing function of the degree of “spreading” of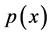 , i.e. the larger
, i.e. the larger 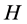 becomes, the spread is
becomes, the spread is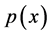 .
.
The Shannon entropy functional was studied just at the beginning of information theory [17] . Since that time, besides the Shannon entropy functional, several other entropy functionals were introduced and studied in the probability theory. The majority of them are dependent on certain parameters. As such, they form a whole family of different functionals (including the Shannon entropy functional as a special case). In a sense, they are a generalization of the Shannon entropy functional. Some of them can equally well express the spread of the probability density functions as differential entropy and are considerably easier to handle mathematically. These include:
(i) The Rényi entropic functional [17]
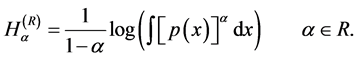 (17)
(17)
(ii) The Havrda-Charvat entropic functional [18]
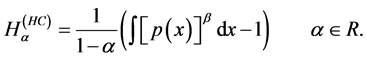 (18)
(18)
(iii) The trigonometric entropic functional [10]
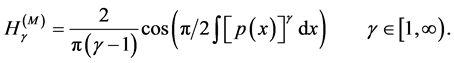 (19)
(19)
Note that 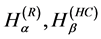 and
and 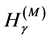 tend to
tend to 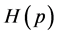 as
as 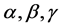 tend to 1. Again, in some instances, it is simpler to compute
tend to 1. Again, in some instances, it is simpler to compute 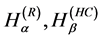 and
and 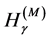 and then recover
and then recover 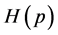 by taking limits
by taking limits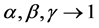 . In treating
. In treating
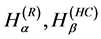 and
and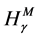 , it is often enough to study the properties of the functional
, it is often enough to study the properties of the functional
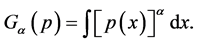
As it is known long ago, the entropy functionals 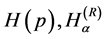 and
and 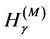 have a mathematical shortcoming connected with the dimension of the physical probability density function. In contrast with the probability which is a dimensionless number, the probability density function has a dimension so that its appearance behind the logarithm and cosine in the entropy functionals
have a mathematical shortcoming connected with the dimension of the physical probability density function. In contrast with the probability which is a dimensionless number, the probability density function has a dimension so that its appearance behind the logarithm and cosine in the entropy functionals 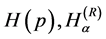 and
and 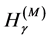 is mathematically inadmissible. This brings complication when calculating
is mathematically inadmissible. This brings complication when calculating 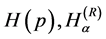 and
and 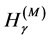 for a physical random variable (see, e.g., [21] )8,9.
for a physical random variable (see, e.g., [21] )8,9.
5. Conclusions
From what has been said so far it follows:
(i) The concept of entropy is inherently connected with the probability distribution of outcomes of a random trial. The entropy quantifies the probability uncertainty of a general random trial.
(ii) There are two ways how to express the uncertainty of a random trial:
The moment and probabilistic measure. The former measure includes in its definition both values assigned to trial outcomes and their probabilities. The latter measure contains in its definition only the corresponding probabilities. The moment uncertainty measures are given as a rule by the higher statistical moments of a random variable whereas the probabilistic measure is expressed by means of entropy. The most important probabilistic uncertainty measure is the Shannon entropy defined by the formula
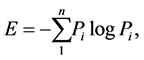
where 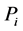 is the probability of i-th outcome of a random trial.
is the probability of i-th outcome of a random trial.
(iii) By means of Shannon entropy it is possible to quantify the configurational order in the set of elements of a general system. The corresponding quantity is called the Watanabe measure of configurational order and is defined as follows configurational order of a system = (sum of entropies of the parts of the system) − (entropy of the whole system).
This measure expresses quantitatively the property of a configurationally organized systems to have order between its elements, which causes that the system as a whole behaves in a more deterministic way than its individual parts.
(iv) The asymptotical equality between the Boltzmann and Shannon entropies for the statistical systems with large particles makes it possible to use the Shannon entropy for describing statistical ensembles.
(v) Besides the Shannon entropy there exists a class of so-called Shannon-like Entropies. The most important Shannon-like entropies are (a) The Rényi entropy Equation (14); (b) The Havrda-Charvat entropy Equation (13). The well-known Tsallis entropy is mathematically identical with Havrda-Charvat entropy.
In conclusion, we can state that the concept of entropy is inherently connected with the probability theory. The application of Shannon entropy in science is really versatile. Besides the mentioned statistical physics, Shannon entropy is used in metronomic, in biological physics, in quantum physics and even in cosmology. Entropy expresses the extent of the randomness of a probabilistic (statistical) system and, therefore, it belongs to the important quantities for describing the natural phenomena. This is why entropy represents in physics a fundamental quantity next the energy.
References
- Feller, W. (1968) An Introduction to Probability Theory and Its Applications. Volume I., John Wiley and Sons, New York
- Boltzmann, L. (1896) Vorlesungen über Gastheorie. J. A. Barth, Leipzig.
- Shannon, C.E. (1948) A Mathematical Theory of Communication . The Bell System Technical Journal, 27, 53-75. http://dx.doi.org/10.1002/j.1538-7305.1948.tb00917.x
- Nyquist, H. (1924) Certain Factors Affecting Telegraph Speed. Bell System Technical Journal, 3, 324 -346. http://dx.doi.org/10.1002/j.1538-7305.1924.tb01361.x
- Khinchin, A.I. (1957) Mathematical Foundation of Information Theory. Dover Publications, New York.
- Aczcél, J. and Daróczy, Z. (1975) On Measures of Information and Their Characterization . Academic Press, New York.
- Merzbacher, E . (1967) Quantum Physics. 7th Edition, John Wiley and Sons, New York.
- Faddejew, D.K. (1957) Der Begriff der Entropie in der Wahrscheinlichkeitstheorie. In: Arbeiten zur Informationstheorie I. DVdW, Berlin.
- Watanabe, S. (1969) Knowing and Guessing. John Wiley and Sons, New York.
- Majerník, V. (2001) Elementary Theory of Organization. Palacký University Press, Olomouc.
- Haken, H. (1983) Advanced Synergetics. Springer-Verlag, Berlin.
- Ke-Hsuch, L . (2000) Physics of Open Systems. Physics Reports, 165, 1-101.
- Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. Physical Review, 106, 620-630. http://dx.doi.org/10.1103/PhysRev.106.620
- Jaynes, E.T. (1967) Foundation s of Probability Theory and Statistical Mechanics. In: Bunge, M., Ed., Delavare Seminar in the Foundation of Physics, Springer, New York. http://dx.doi.org/10.1007/978-3-642-86102-4_6
- Ang, A.H. and Tang, W.H. (2004) Probability Concepts in Engineering. Planning, 1, 3-5.
- Vajda, I. (1995) Theory of Information and Statistical Decisions. Kluver, Academic Publisher, Dortrecht.
- Rényi, A. (1961) On the Measures of Entropy and Information . 4th Berkeley Symposium on Mathematical Statistics, 547-555.
- Havrda, J. and Charvát, F. (1967) Quantification Method of Classification Processes. Concept of Structural
 -Entropy. Kybernetika, 3, 30-35.
-Entropy. Kybernetika, 3, 30-35. - Majerník, V. Majerníkova, E. and Shpyrko, S. (2003) Uncertainty Relations Expressed by Shannon-Like Entropies. Central European Journal of Physics, 6, 363-371. http://dx.doi.org/10.2478/s11534-008-0057-6
- Tsallis, C. (1988). Possible Generalization of Boltzmann-Gibbs Statistics. Journal of Statistical Physics, 52, 479-487. http://dx.doi.org/10.1007/BF01016429
- Majerník, V. and Richterek L. (1997) Entropic Uncertainty Relations. European Journal of Physics, 18, 73-81. http://dx.doi.org/10.1088/0143-0807/18/2/005
- Brillouin, L. (1965) Science and Information Theory. Academic Press, New York.
- Flower, T.B. (1983) The Notion of Entropy. International Journal of General Systems, 9, 143-152.
- Guiasu, S. and Shenitzer, A. (1985) The Principle of Maximum Entropy. The Mathematical Intelligencer, 7, 42-48. http://dx.doi.org/10.1007/BF03023004
- Khinchin, A.I. (1957) Mathematical Foundation of Information Theory. Dover Publications, New York.
- Chaitin, G.J. (1982) Algorithmic Information Theory. John Wiley and Sons, New York.
- Kolmogorov, A.N. (1965) Three Approaches to the Quantittative Definition of Information . Problems of Information Transmission, 1, 1-7.
Appendix
The Essential Mathematical Properties of Entropy
We ask from the Shannon entropy the following desirable properties [24] :
(i) 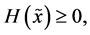 is a continuous function of all components of a probability distribution of a random variable
is a continuous function of all components of a probability distribution of a random variable 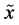 which is invariant under any permutation of the indices of the probability components.
which is invariant under any permutation of the indices of the probability components.
(ii) If probability distribution of 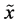 has only one component which is different from zero then
has only one component which is different from zero then 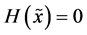
(iii) For 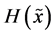 it holds
it holds
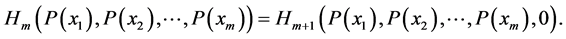 (A1)
(A1)
(iv)
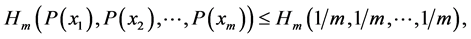 (A2)
(A2)
with equality if and only if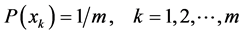 .
.
(v) If 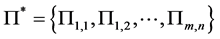 is a joint probability distribution whose marginal probability distributions are
is a joint probability distribution whose marginal probability distributions are 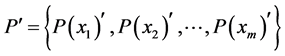 and
and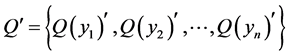 , respectively, then
, respectively, then
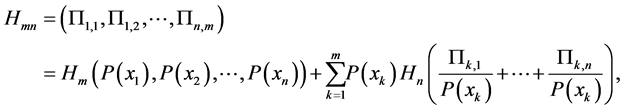 (A3)
(A3)
where the conditional entropy, defined as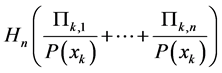 , is computed only for those values of
, is computed only for those values of 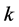 for which
for which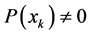 .
.
(vi) Using notation given above it holds
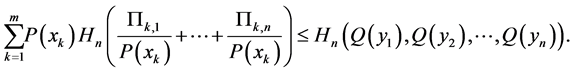 (A4)
(A4)
The equality in (A4) is valid if and only if
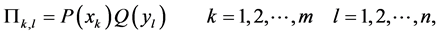
in which case (A3) becomes
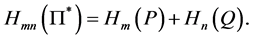
All these properties can be proved in an elementary manner. Without entering into the technical details, we note that properties (i)-(iii) are obvious while property (v) can be obtained by a straightforward computation taking into account only the definition of entropy. Finally, from Jensen’s inequality
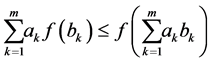
applied to the concave function 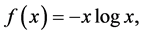 we obtain property (iv) by putting,
we obtain property (iv) by putting, 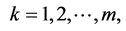
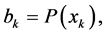
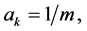 and the inequality (A4) by putting
and the inequality (A4) by putting 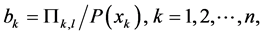
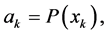 and, in the last case, summing the resulting
and, in the last case, summing the resulting 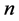 inequalities.
inequalities.
Interpretation of the above properties agrees with common sense, intuition, and the reasonable requirements that can be asked from a measure of uncertainty. Indeed, a random experiment which has only one possible outcome (that is, a strictly deterministic trial) contains no uncertainty at all; we know what will happen before performing the experiment . This is just property (ii). If to the possible outcomes having the probability zero, the amount of uncertainty with respect to what will happen in the trial remains unchanged (property (iii)). Property (iv) tells us that in the class of all probabilistic trials having 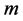 possible outcomes, the maximal uncertainty is contained in the special probabilistic trial whose outcomes are equally likely. Before interpreting the last properties let us consider two discrete random variable
possible outcomes, the maximal uncertainty is contained in the special probabilistic trial whose outcomes are equally likely. Before interpreting the last properties let us consider two discrete random variable 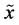 and
and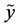 , whose ranges contain
, whose ranges contain 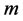 and
and 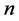 numerical values, respectively. Using the notations as in property (v), suppose that
numerical values, respectively. Using the notations as in property (v), suppose that 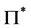 is the joint probability distribution of the pair
is the joint probability distribution of the pair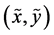 , and
, and 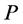 and
and 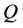 are the marginal probability distributions of
are the marginal probability distributions of 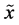 and
and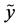 , respectively. In this case equality iii may be written more compactly
, respectively. In this case equality iii may be written more compactly
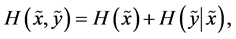 (A5)
(A5)
where
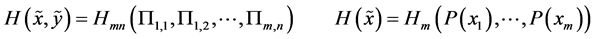
and
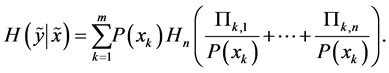
Here 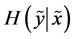 is the conditional entropy of
is the conditional entropy of 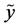 given
given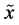 . According to (v), the amount of uncertainty contains in a pair of random variables (or, equivalently, in compoundor product-probabilistic trial) is obtained by summing the amount of uncertainty contained in
. According to (v), the amount of uncertainty contains in a pair of random variables (or, equivalently, in compoundor product-probabilistic trial) is obtained by summing the amount of uncertainty contained in 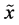 and the uncertainty contained in
and the uncertainty contained in 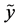 conditioned by random variable
conditioned by random variable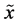 . Similarly, we get
. Similarly, we get
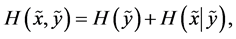 (A6)
(A6)
where
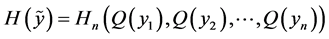
and
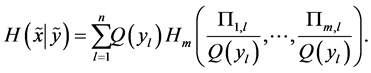
Here
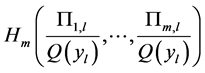
is the conditional entropy of 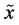 given the
given the 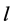 -th value of
-th value of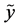 .
. 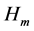 is defined only for those values of
is defined only for those values of 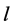 for which
for which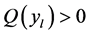 . From (A5) and (A6) we get
. From (A5) and (A6) we get
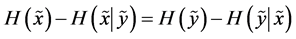
which is the so-called “uncertainty balance”, the only conservation law for entropy.
Finally, property (vi) shows that some data on 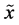 can only decrease the uncertainty on
can only decrease the uncertainty on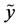 , namely
, namely
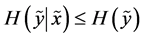 (A7)
(A7)
with equality if and only if 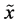 and
and 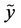 are independent. From (A5) and (A7) we get
are independent. From (A5) and (A7) we get
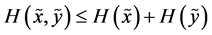
with equality if and only if 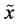 and
and 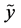 are independent.
are independent.
Fortunately this inequality holds for any number of components. More generally, for 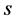 random variables with arbitrary finite range we can write
random variables with arbitrary finite range we can write
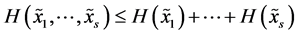
with equality if and only if 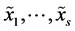 are globally independent. Therefore
are globally independent. Therefore
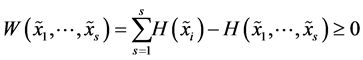 (A8)
(A8)
measures the global dependence between the random variables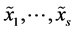 , that is, the extent to which the system
, that is, the extent to which the system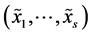 , due to interdependence, makes up “something more” that the mere juxtaposition of components. In particular,
, due to interdependence, makes up “something more” that the mere juxtaposition of components. In particular, 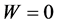 if and only if
if and only if 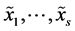 are independent.
are independent.
Note that the difference between the amount of uncertainty contained by the pair 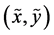 and the amount of dependence between the components
and the amount of dependence between the components 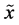 and
and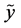 , namely
, namely
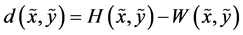
or, equivalently,
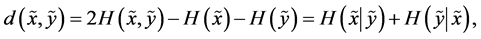
is the distance between the random variables 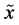 and
and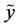 , with the two random variables considered identical if either one completely determines the other, or if
, with the two random variables considered identical if either one completely determines the other, or if 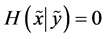 and
and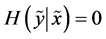 . Therefore, the “pure randomness” contained in the pair
. Therefore, the “pure randomness” contained in the pair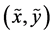 , i.e., the uncertainty of the whole, minus the dependence between the components, measured by
, i.e., the uncertainty of the whole, minus the dependence between the components, measured by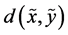 , is a distance between
, is a distance between 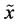 and
and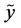 .
.
Khintchin [25] proved that properties (i), (iii), (iv) and (v), taken as axioms imply uniquely the formula of the Shannon entropy (except an numerical factor). It is worthy to remark that there is also another way to determine the uncertainty of a probabilistic object. The Shannon entropy is a measure of the degree of uncertainty of random object whose probability distribution is given. In algorithmic theory, the primary concept is that of the information content of an individual object, which is a measure of how difficult it is to specify or describe and how to construct or calculate that object. This notion is also known as information-theoretical complexity. The information content 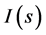 of a binary string
of a binary string 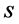 is defined to be the size in bits of the smallest program for a canonical universal computer to calculate s [26] [27] .
is defined to be the size in bits of the smallest program for a canonical universal computer to calculate s [26] [27] .
NOTES

1The concept of probability was mathematically clarified and rigorously determined about sixty years ago. The probability is interpreted as a complete measure on the σ-algebra γ of the subsets S1, S2,···Sn of the set of the elementary random events B. The probability measure P fulfils following relations:
(i) 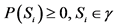
(ii) From 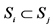 it follows
it follows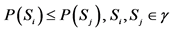 .
.
(iii) If 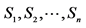 are such elements of σ-algebra γ, for which
are such elements of σ-algebra γ, for which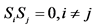 , then it holds the following equation:
, then it holds the following equation:
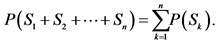
(iv)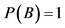 .
.
The σ-algebra, on which the set function P is defined, is called the Kolmogorov probability algebra. The triplet 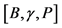 denotes the probability space. Under a random variable
denotes the probability space. Under a random variable 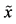 we understand each real-valued measurable function defined on the elementary random events B .
we understand each real-valued measurable function defined on the elementary random events B .
2The word “entropy” stems from the Greek word “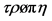 ” which means “transformation”.
” which means “transformation”.
3Entropy is sometimes called “missing information”.

4The probability as well as the Shannon entropy is dimensionless quantities. On the other side, the thermodynamical entropy has the physical dimension equal to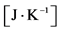 . Therefore, in order to get the correct physical dimension for the thermodynamic entropy we must multiply the Shannon entropy by the Boltzmann constant, which has the value
. Therefore, in order to get the correct physical dimension for the thermodynamic entropy we must multiply the Shannon entropy by the Boltzmann constant, which has the value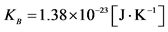 .
.

5The Havrda-Charvat 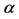 -entropy exactly matches the Tsallis non-extensive entropy of statistical physics.
-entropy exactly matches the Tsallis non-extensive entropy of statistical physics.
6The Tsallis entropy which is mathematically identical with the Havrda-Charvat 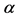 -entropy , was introduced by two mathematicians Havrda and Charvat in sixties, violates the additivity property which is considered as an essential property of physical entropy. This is why the other Shannon-like entropies could be more suitable for formulation of an alternative statistical physics.
-entropy , was introduced by two mathematicians Havrda and Charvat in sixties, violates the additivity property which is considered as an essential property of physical entropy. This is why the other Shannon-like entropies could be more suitable for formulation of an alternative statistical physics.

7In order to apply the formula for the Shannon entropy for the continuous random variable 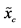 with the probability density function
with the probability density function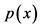 , we divide the
, we divide the 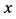 -axis into
-axis into 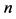 equidistant intervals. The probability that
equidistant intervals. The probability that 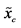 assumes value from the interval
assumes value from the interval 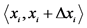 is
is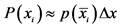 , where
, where 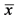 is from
is from 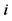 -th interval. Inserting
-th interval. Inserting 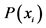 into the Shannon entropy we have
into the Shannon entropy we have
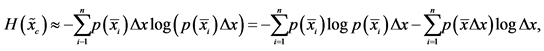
Passing to the infinitesimal interval, we obtain
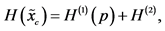
where
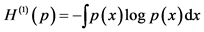
and
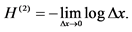
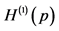 is the Shannon entropy functional.
is the Shannon entropy functional.

8It is typical for the entropy and even for the probability itself that their uncertainty measures are determined trough a set of certain reasonable requirements (axioms), therefore they are more “abstract” than the measures, e.g., for work or energy in physics. Physical quantities are mostly derived from the concepts of motion or field which are more concrete than the concept of probability and entropy.
9In many textbook and also in some advanced books, Shannon entropy and information are used so as if were synonymous. This can be confusing and may lead to the some conceptual shortcomings. Especially, the Brillouin’s use of the concept of information, which he used in his celebrated work “Science and Information Theory” , has been often criticized (see, e.g. ).