Received 12 May 2015; accepted 2 June 2015; published 5 June 2015

ABSTRACT

In this paper, we obtain unique common fixed point theorems for two mappings satisfying the variable coefficient linear contraction of integral type and the implicit contraction of integral type respectively in metric spaces.

Keywords:

Contractive Mapping of Integral Type, Common Fixed Point, Metric Space

1. Introduction and Preliminaries

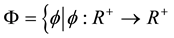Throughout this paper, we assume that and satisfying that is Lebesgue

integral, summable on each compact subset of 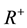and for each.

The famous Banach’s contraction principle is as follows:

Theorem 1.1 ([1] ). Let f be a self mapping on a complete metric space 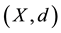satisfying

(1.1)

where 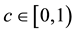is a constant. Then f has a unique fixed point 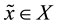such that 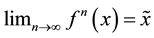for each.

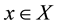It is known that the Banach contraction principle has a lot of generalizations and various applications in many directions; see, for examples, [2] - [15] and the references cited therein. In 1962, Rakotch [11] extended the Banach contraction principle with replacing the contraction constant c in (1.1) by a contraction function 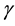and obtained the next theorem.

Theorem 1.2 ( [11] ). Let f be a self-mapping on a complete metric space 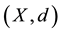satisfying

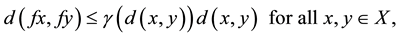(1.2)

where 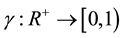is a monotonically decreasing function. Then f has a unique fixed point such that for each.

In 2002, Branciari [12] gave an integral version of Theorem 1.1 as follows.

Theorem 1.3 ( [12] ). Let f be a self-mapping on a complete metric space satisfying

(1.3)

where is a constant and. Then f has a unique fixed point such that

for each.

In 2011, Liu and Li [13] modified the method of Rakotch to generalize the Branciari’s fixed point theorem with replacing the contraction constant c in (1.3) by contraction functions and and established the following fixed point theorem:

Theorem 1.4 ([13] ). Let f be a self-mapping on a complete metric space satisfying

(1.4)

where and are two functions with

for all;; for all.

Then f has a unique fixed point such that for each.

Here, we will use the methods in [3] [9] [13] to discuss the unique existence problems of common fixed points for two self-mappings satisfying two different contractive conditions of integral type in a complete metric space.

2. Common Fixed Point Theorems

Lemma 2.1 ([13] ). Let and be a nonnegative sequence with. Then

.

Lemma 2.2([13] ). Let and be a nonnegative sequence. Then

Now, we will give the first main result in this paper.

Theorem 2.1. Let be a complete metric space, two mappings. If for each,

(2.1)

where and are three functions satisfying the following conditions

(2.2)

(2.3)

Then f and g have a unique common fixed point u, and the sequence defined by, for any converges to u.

Proof.

Let. We construct a sequence satisfying the following conditions, for all. Let for all.

For, by (2.1),

hence by (2.3),

(2.4)

Similarly, by (2.1),

hence by (2.3),

(2.5)

Combining (2.4) and (2.5), we have

(2.6)

Now, we prove that

(2.7)

Otherwise, there exists such that

(2.8)

Obviously,. If, then by (2.3), (2.4), (2.6) and (2.8),

which is a contradiction. Similarly, if, then by (2.3), (2.5), (2.6) and (2.8),

which is also a contradiction. Hence (2.7) holds. Therefore there exists such that. If, then by Lemma 2.1, (2.3) and (2.4),

which is a contradiction. Therefore, that is,.

We claim that is a Cauchy sequence. Otherwise, there such that for, there exist with such that the parity of and is different and

For k, let denotes the least integer exceeding and satisfying the above, then

(2.9)

hence

(2.10)

Let, then we obtain. But

hence we obtain

(2.11)

If is even and is odd, then by Lemma 2.1, (2.11) and (2.1),

which is a contradiction. Similarly, we obtain the same contradiction for the case that is odd and is even. Hence is a Cauchy sequence, therefore for some by the completeness of X.

If, then, hence by (2.1) and Lemma 2.1,

which is a contradiction, hence. Similarly, we obtain. Therefore is a common fixed point of f and g.

If is another common fixed point of f and g, then, hence by (2.1),

which is a contradiction, hence, i.e., is the unique common fixed point of f and g.

From Theorem 2.1, we obtain the next more general common fixed point theorem.

Theorem 2.2. Let be a complete metric space, and two mappings. If for each,

(2.12)

where, are three functions satisfying (2.2) and (2.3). Then f and g have a unique common fixed point u, and the sequence defined by for any converges to u.

Proof.

Let and, then F and G satisfy all of the conditions of Theorem 2.1, hence there exists an unique element such that. If, then, hence by (2.12),

which is a contradiction, hence. Similarly,. So u is a common fixed point of f and g. The uniqueness is obvious.

From now on, we will discuss the second common fixed point problem for two mappings with implicit contraction of integral type.

Let if and only if is a continuous and non-decreasing function about the 4th and 5th variables and satisfying the following conditions:

(i) There exists such that implies;

(ii) There exists such that implies;

(iii) for all.

Example 2.1. Define as follows

where for all and. Then.

The function is called to be sub-additive if and only if for all,

Example 2.2. Let for each. Then obviously and for all,

Hence is a sub-additive function.

Theorem 2.3. Let be a complete metric space, two mappings. If for each,

(2.13)

where is sub-additive and. Then f and g have a unique common fixed point.

Proof.

We take any element and consider the sequence constructed by and for all. Let for all.

Since

So by (i),

(2.14)

Similarly,

So by (ii),

(2.15)

Combining (2.14) and (2.15), we have

(2.16)

Obviously, for all. If there exits such that, then. If, then by (2.14) and (2.16)

which is a contradiction. Similarly, if, then by (2.15) and (2.16)

which is also a contradiction. Hence we have

Therefore there exists . If, then

which is a contradiction. Therefore, , i.e.,

We claim that is Cauchy. Otherwise, just as the line of proof of Theorem 2.1, there exists such that for there exist with such that the parity of and is different and (2.11) holds.

If is even and is odd, then by Lemma 2.1, (2.11), (2.13) and (iii),

This is a contradiction. Similarly, we obtain the same contradiction for the case that is odd and is even. Therefore, is a Cauchy sequence. Let.

If, then, hence by Lemma 2.1 and (2.13) and (iii),

which is a contradiction, hence. Similarly, we obtain. Therefore, is a common fixed point of f and g.

If is another common fixed point of f and g, then, hence by (2.13) and (iii),

This is a contradiction. Hence is the unique common fixed point of f and g.

Using Theorem 2.3 and the Example 2.2, we have the next result.

Theorem 2.4. Let be a complete metric space, two mappings. If

where. Then f and g have a unique common fixed point u.

Combining Theorem 2.4 and Example 2.1, we obtain the following result.

Theorem 2.5. Let be a complete metric space, two mappings. If for each,

where for all and. Then f and g have a unique common.

Acknowledgements

The research is partially supported by the National Natural Science of Foundation of China (No. 11361064).

References

NOTES

^*Corresponding author.