Applied Mathematics
Vol.4 No.5(2013), Article ID:31472,9 pages DOI:10.4236/am.2013.45113
Magnetohydrodynamic (MHD) Free Convective Flow past an Infinite Vertical Porous Plate with Joule Heating
1Department of Pure and Applied Mathematics, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya
2School of Mathematics and Statistics, The Kenya Polytechnic University College, Nairobi, Kenya
Email: jksigey2002@yahoo.com, masenooj@gmail.com, ngjs9@yahoo.com, kgatheri@yahoo.com
Copyright © 2013 Sigey K. Johana et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 21, 2012; revised March 28, 2013; accepted April 4, 2013
Keywords: Incompressible Flow; Electrically Conducting; Joule Heating
ABSTRACT
This work addresses the problem of Magnetohydrodynamic laminar unsteady flow of an incompressible electrically conducting fluid past an infinite vertical porous plate. It investigates how joule heating affects the velocity and temperature profiles of the fluid flow subjected to transverse magnetic field. The research examines specific equations of MHD flow which are solved numerically by finite difference approximations, using computer programme. The numerical results of this study reveal that an increase in joules heating parameter causes an increase in the velocity and temperature profiles uniformly near the plate but remain constantly distributed away from the plate, implying that the flow field of the MHD free convective flow is influenced substantially by the strength of Joules heating near the wall of the plate and at the mainstream.
1. Introduction
MHD is the discipline that studies the dynamics of electrically conducting fluids. Examples of such fluids include plasma, liquid metals and salt water. The word MHD (Magneto Hydrodynamics) is derived from magneto-meaning magnetic field, and hydro-meaning liquid and dynamics meaning mechanical properties of fluid. Hydrodynamics on the other hand is the study of fluid flow and the forces that cause the flow in the absence of an electromagnetic field. We consider a fluid to be any matter that under goes deformation when an external force is applied. In MHD a current is induced when the fluid conductor moves in magnetic field. As a result, when a conducting fluid flows in the presence of a transverse magnetic field, electromagnetic forces act on the fluid particles thereby altering their geometry of motion. The momentum equation describing the motion of fluid in MHD includes body forces which act on fluid particles from a distance. The applied magnetic fields act on both electronic and ionized atoms to produce dynamic effect. This mass motion in turn produces modification in the electromagnetic field. Heat transfer in fluid is by conduction, convection and radiation. In convection an essential step in the problem is to determine whether the boundary layer is Laminar or turbulence. Surface friction and convection transfer rates depend strongly on which of the conditions exists. Laminar fluid appears to move by sliding of lamination of infinitesimal thickness relative to adjacent layers. In most of the free convective flow investigations the heat transfer, temperature distributions, velocity profiles and turbulence intensities are mostly obtained by means of either experimental methods or numerical methods which have comparatively large flexibility in geometry and boundary conditions governing motion. The mechanical motion of the system can then be described in terms of a single conducting fluid with hydro magnetic variables of density, velocity and pressure. At low frequencies it is customary to neglect the displacement current in Amperes law. This is then the approximation called magneto hydrodynamics.
Turbulent flow occurs when there are disturbances present in a fluid due to a variety of factors such as porous plates, boundary roughness and variation in the physical properties of fluid motion among others. Joule heating means the heat produced when current flows through a device (conductor), this heating can then lead to thermal stresses which will force the device to bend due to fact that the upper part is narrower than the lower part. The set of equations describing MHD is a combination of Navier-Stokes equations of fluid dynamics and Maxwell’s equations of electromagnetism (differential equations) which can be solved simultaneously either analytically or numerically.
1.1. Definition of Terms@NolistTemp#1.1.1. Mass Transfer
Convection mass transfer involves the transport of materials between boundary surface and moving fluid. Mass transport always plays an important role in many industrial processes for example, removal of pollutants from plant discharge.
1.1.2. Heat Transfer
Convection heat transfer involves the energy exchange between a boundary surface and an adjacent fluid due to temperature variations.
1.1.3. Free Convection
In free convections, the fluid motion is as a result of density gradients created by temperature or concentration gradients existing in fluid.
1.1.4. Joule Heating
It is the process by which the passage of an electric current through a conductor releases heat. It is caused by interaction between the moving particles that form the current (usually, but not always, electrons) and the atomic ions that make up the body of the conductor. Charged particles in an electric circuit are accelerated by an electric field but give up some of their kinetic energy each time they collide with an ion. The increase in the kinetic or vibration energy of the ions manifests itself as heat and a rise in the temperature of the conductor. Hence energy is transferred from the electrical power supply to the conductor and any material with which it is in thermal contact.
The first research in magneto hydrodynamics was done by Faraday [1] who performed an experiment on the behavior of current in circuits placed in time-varying magnetic fields. In his experiment with mercury as the conducting fluid flowing in a glass tube placed in a magnetic field, he observed that a voltage was induced in a direction perpendicular to both the direction of the flow and magnetic field.
When an electric field is applied to conducting fluid in a direction perpendicular to a magnetic field a force is exerted on the fluid in a direction perpendicular to both the electric field and magnetic field.
Calvert L. [2] composed his research article on the fundamental principle of MHD where he showed that the effect of magnetic field on conducting fluid in motion is to exert a force perpendicular to the magnetic field that tends to make normal velocity equal to the  drifts. He asserted that the higher the conductivity, the stronger is this force and the closely is the magnetic field dragged by the fluid (and vice versa) and that the motion of the fluid along the direction of the magnetic field is unaffected. Ramulu et al. [3] studied the effect of hall current on MHD flow and heat transfer along a porous flat plate with mass transfer. He applied numerical methods to obtain the solution. Cooker et al. [4] investigated the influence of viscous dissipation and radiation on problem of unsteady magneto hydrodynamics free-currents flow past an infinite heated vertical plate in an optically thin environment with time dependent suction. The results shows that increasing cooling
drifts. He asserted that the higher the conductivity, the stronger is this force and the closely is the magnetic field dragged by the fluid (and vice versa) and that the motion of the fluid along the direction of the magnetic field is unaffected. Ramulu et al. [3] studied the effect of hall current on MHD flow and heat transfer along a porous flat plate with mass transfer. He applied numerical methods to obtain the solution. Cooker et al. [4] investigated the influence of viscous dissipation and radiation on problem of unsteady magneto hydrodynamics free-currents flow past an infinite heated vertical plate in an optically thin environment with time dependent suction. The results shows that increasing cooling  of the plate and Eckert members leads to arise in the velocity profile while increases in magnetic field, radiation and Darcy’s parameters are associated with decrease in the velocity. Jordan J. [5] analyzed the effect of thermal radiation and viscous dissipation and MHD free convection flow over a semi-infinite vertical porous plate. The network simulation method is used to solve the boundary layer equations based on the finite difference formulations. It was found that increase in viscous dissipation leads to an increase of both velocity and temperature profiles, an increase in magnetic parameter leads to an increase in the temperature profiles and a decrease in the velocity profiles finally an increase in the suction parameter leads to an increase in the local skin friction and Nusselt number. Emad et al. [6] studied the effect of viscous dissipation and joule heating on MHD free convection flow past a semi-infinite vertical flat plate in presence of the combined effect of Hall and Ion-slip currents for the case of power-law variation of the wall temperature. They found that the magnetic field acts as a retarding force on the tangential flow but has a propelling effect on the induced lateral flow. The skin-friction factor for the tangential floe and the Nusselt number decreases but the skin-friction factor for the tangential and lateral flows is increased while the local Nusselt number is decreased if the effect of viscous dissipation, joule heating and heat generation are considered. Hall and Ion-slip terms were ignored in applying Ohm’s law as it has no marked effect for small and moderate values of the magnetic field.
of the plate and Eckert members leads to arise in the velocity profile while increases in magnetic field, radiation and Darcy’s parameters are associated with decrease in the velocity. Jordan J. [5] analyzed the effect of thermal radiation and viscous dissipation and MHD free convection flow over a semi-infinite vertical porous plate. The network simulation method is used to solve the boundary layer equations based on the finite difference formulations. It was found that increase in viscous dissipation leads to an increase of both velocity and temperature profiles, an increase in magnetic parameter leads to an increase in the temperature profiles and a decrease in the velocity profiles finally an increase in the suction parameter leads to an increase in the local skin friction and Nusselt number. Emad et al. [6] studied the effect of viscous dissipation and joule heating on MHD free convection flow past a semi-infinite vertical flat plate in presence of the combined effect of Hall and Ion-slip currents for the case of power-law variation of the wall temperature. They found that the magnetic field acts as a retarding force on the tangential flow but has a propelling effect on the induced lateral flow. The skin-friction factor for the tangential floe and the Nusselt number decreases but the skin-friction factor for the tangential and lateral flows is increased while the local Nusselt number is decreased if the effect of viscous dissipation, joule heating and heat generation are considered. Hall and Ion-slip terms were ignored in applying Ohm’s law as it has no marked effect for small and moderate values of the magnetic field.
Kinyanjui et al. [7] investigated unsteady free convection in compressible fluid past a semi-infinite vertical porous plate in the presence of a strong magnetic field inclined at an angle to the plate with Hall and ion-slip currents effects. The effects of modified Grashof number, suction velocity, the angle of inclination, time, Hall current, ion-slip current, Eckert number, Schmidt number and heat source parameter on the convectively cooled or convectively heated plate restricted to Laminar boundary layer were studied. He found that an increase in mass diffusion parameter Sc cause an increase in the concentration profile, an increase in Eckert number Ec causes an increase in temperature profile and also an increase in the angle of inclination leads to an increase in primary velocity profiles but a decrease in secondary profiles.
Duwairi G. [8] analyzed viscous and joule heating effect on forced convection flow of ionized gases adjacent to isothermal porous surfaces, he analyzed his equations numerically and found that heat transfer rate is decreased due to viscous dissipation effect in both the cases of suction or injection in the fluid.
It is for this purpose that we investigate MHD free convective flow of an incompressible conducting fluid past an infinite vertical porous plate with joule heating in presence of a uniform transverse magnetic field.
1.2. Application
Velocity profiles play an important role in many industrial processes, for example; the removal of pollutants from plant discharge streams by absorptions and stripping of gases from waste water entirely depend on relative rate of velocity profiles distribution. Pollutant removal is the process of reducing or eliminating the release of pollutants into the environment. It is regulated by the various environmental agencies which establish pollutant discharge limits for air, water and land. Air pollution control includes particulate emission and gaseous emission which can be done by many kinds of equipments which operate on the velocity distribution principle to reduce the emissions.
Physical separation of the particulate from the air using settling chambers, cyclone collectors, impingers, wet scrubbers, electrostatic precipitators and filtration devices are all processes that are typically employed. Settling chambers use gravity separations to reduce particulate emissions. The air stream is directed through a settling chamber which is relatively long and has large cross section causing the velocity of the air stream to be greatly decreased and allowing sufficient time for the settling of solid particles. Flaring and incineration take advantage of the combustibility of a gaseous pollutant. In general, excess air is added to these processes to drive the combustion reaction to completion forming carbon dioxide and water.
In the physical water treatment systems which rely on physical forces to aid in the removal of pollutant like screening, filtration, sedimentation and flotation. Sedimentation devices utilize gravity to remove the heavier particles from the water stream. The wide array of sedimentation basins in use slow down the water velocity in the unit to allow time for particles to drop to the bottom. Likewise flotation uses difference in particle densities which in this case are lower than water, to effective removal.
Operating principles of certain MHD devices utilizes the interaction between velocity field, magnetic field and electric field. Any device designed in this manner is capable of performing the functions of various machines. The particular devices where these principles are applied include MHD generators, MHD flow meter, MHD pump and heat exchanger.
2. Geometry of the Problem
The Figure 1 below shows the geometry of the problem discussed. The x-axis is taken along the plate in vertically upward direction which is the direction of flow. The y-axis is taken normal to plate. Since the plate is infinite in length and for a two dimensional free convective fluid flow the physical variables are functions of x, y and t.
3. Specific Equations Governing Fluid Flow
Free convection magneto hydrodynamic fluid flow pastinfinite vertical porous plate subjected to a uniform magnetic field and constant suction velocity is considered.
3.1. Momentum Equation
The equation of momentum is derived from the Newton second law of motion which states that the total body force and surface forces acting on a system is equal to the time rate of change of the momentum of the system. In vector notation, the equation of motion considering the body force due to gravity and electromagnetic force only may be written as;
 (1)
(1)
In component form and in x-direction

Figure 1. Flow configuration.
 (2)
(2)
where 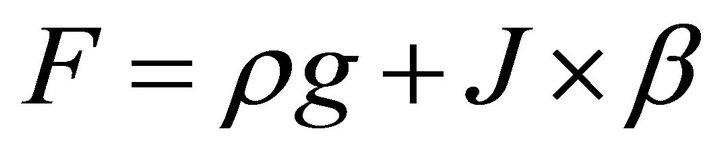 since we are considering both gravitational force g and electromagnetic force in order to get the volumetric density of the external force. To determine the pressure gradient, the momentum equation is evaluated at the edge of the boundary layer where
since we are considering both gravitational force g and electromagnetic force in order to get the volumetric density of the external force. To determine the pressure gradient, the momentum equation is evaluated at the edge of the boundary layer where  and
and . Pressure term in x direction
. Pressure term in x direction
 results from the change in the elevation.
results from the change in the elevation.
The body force term in Equation (2) along negative x-direction is . Combining the two terms give
. Combining the two terms give
 . The current density
. The current density
 where
where . From the equation of conservation of electric charges
. From the equation of conservation of electric charges , J = 0 = constant, this constant must be zero, since
, J = 0 = constant, this constant must be zero, since  at the plate which is electrically non conducting, hence
at the plate which is electrically non conducting, hence 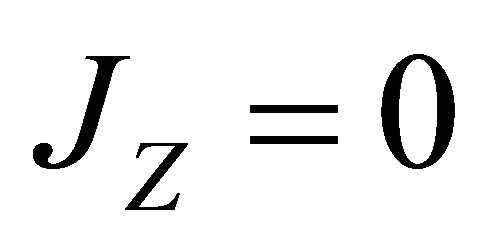 everywhere in the flow.
everywhere in the flow.  due to the geometrical nature of the problem. Thus
due to the geometrical nature of the problem. Thus . Substituting in Equation (2), the momentum equation reduces to;
. Substituting in Equation (2), the momentum equation reduces to;
 (3)
(3)
and in y-direction the equation reduces to
 (4)
(4)
if we define the volumetric coefficients of the thermal expansion by
 then
then . Substituting in Equations (3) and (4) the final momentum equation for this study in the x and y directions respectively become;
. Substituting in Equations (3) and (4) the final momentum equation for this study in the x and y directions respectively become;
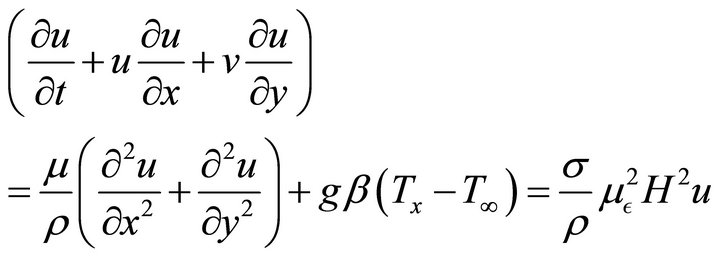 (5)
(5)
 (6)
(6)
Method of Solution
Equations governing fluid flow in our study are nonlinear, thus, their exact solutions are difficult to obtain. We thus employed a fast and stable method in order to solve these differential equations.
The Finite difference method used in solving these differential equations satisfied basic requirements such as consistency, stability and convergence. A method is convergent if as more grid points are taken or step size decreased, the numerical solution converges to the exact solution. A method is stable if the effect of any single fixed round off error is bounded.
Finally a method is consistent if the truncation error tends to zero as the step size decreases. The numerical error arises because in most computations we cannot exactly compute the difference solution as we encounter round off errors. In fact in some cases the exact solution may differ considerably from the difference solution. If the effect of the round off error remains bounded as the mesh points tend to infinity with fixed sizes, then the difference method is said to be stable.
In this study we use subscripts to indicate spatial points and superscript to indicate time . Let the mesh point variable at time
. Let the mesh point variable at time ![]() be denoted by
be denoted by . The forward difference for the first order derivatives with respect to time t is given by
. The forward difference for the first order derivatives with respect to time t is given by
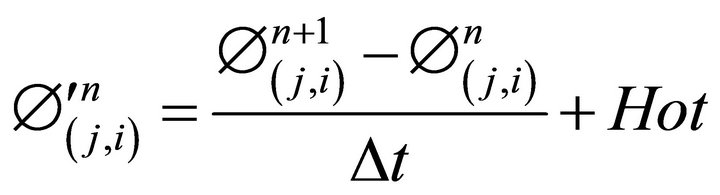 (7)
(7)
Use forward finite difference for the first order time derivative and central finite difference for the first and second spatial derivative. The final set of the governing equations from Equations (5) to (6) in finite difference form are
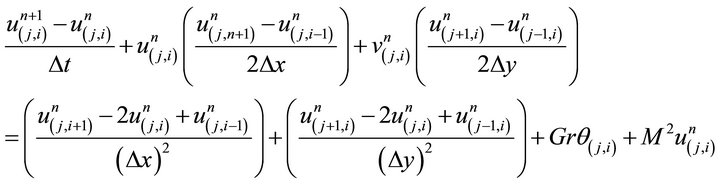 (8)
(8)
 (9)
(9)
Making  and
and  the subjects yields;
the subjects yields;
 (10)
(10)
and
 (11)
(11)
respectively.
The initial conditions take the form:
![]() (12)
(12)
![]() (13)
(13)
For 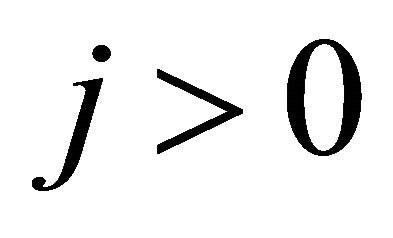 and all
and all , the boundary condition take the form;
, the boundary condition take the form;
![]() (14)
(14)
 (15)
(15)
The initial and boundary conditions for non-dimensional form for energy equation with time t are:
For
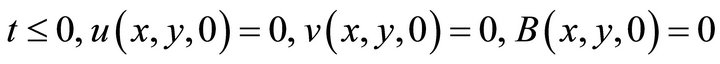
For
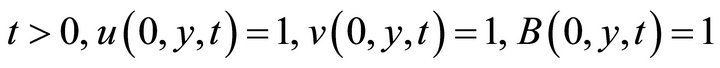
For
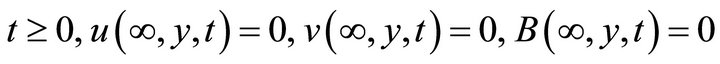
The computations are performed using small values of . In our research, we set
. In our research, we set  and
and 
 . We fixed
. We fixed  that is
that is  as corresponding to
as corresponding to . The velocities
. The velocities  and
and  are computed from Equations (10) and (11).
are computed from Equations (10) and (11).
This procedure is repeated until  that is
that is  for
for![]() ,
, .
.
In our calculations the Prandtl number is taken as 0.71 which corresponds to air, magnetic parameter  which signifies a strong magnetic field. We consider one case, that is, when the
which signifies a strong magnetic field. We consider one case, that is, when the  corresponding to convective cooling of the plate.
corresponding to convective cooling of the plate.
To ensure stability and convergence of the finite difference method, Java computer program is run using smaller values of![]() , that is
, that is ![]() = 0.0007, 0.005, 0.0015.
= 0.0007, 0.005, 0.0015.
3.2. Energy Equation

Solving it using the finite difference method yields;
 (16)
(16)
4. Results
To obtain numerical results in tables and graphs for this work, we solved equations by finite difference method (Equations (10), (11) and (16)) were run using Java computer programme after setting the initial and boundary conditions as in Equations (14) to (15). The computed results are then discussed bellow.
From Table 1 and Figure 2, for,  , we observe that, the primary velocity profile increases rapidly with an increase in joules parameter R near the plate and maintains constant velocity profile distribution far away from the plate.
, we observe that, the primary velocity profile increases rapidly with an increase in joules parameter R near the plate and maintains constant velocity profile distribution far away from the plate.
From Table 2 and Figure 3, for  we observe that, the secondary velocity profile distribution remain constantly zero near the plate up to a certain distance from the plate when they begin to increase uniformly with an increase in joules parameter R before resuming a constant distribution far away from the plate.
we observe that, the secondary velocity profile distribution remain constantly zero near the plate up to a certain distance from the plate when they begin to increase uniformly with an increase in joules parameter R before resuming a constant distribution far away from the plate.
From Table 3 and Figure 4, for , we observe that, very close to the plate the rate of Temperature profiles distribution is zero but after some reasonable distance
, we observe that, very close to the plate the rate of Temperature profiles distribution is zero but after some reasonable distance
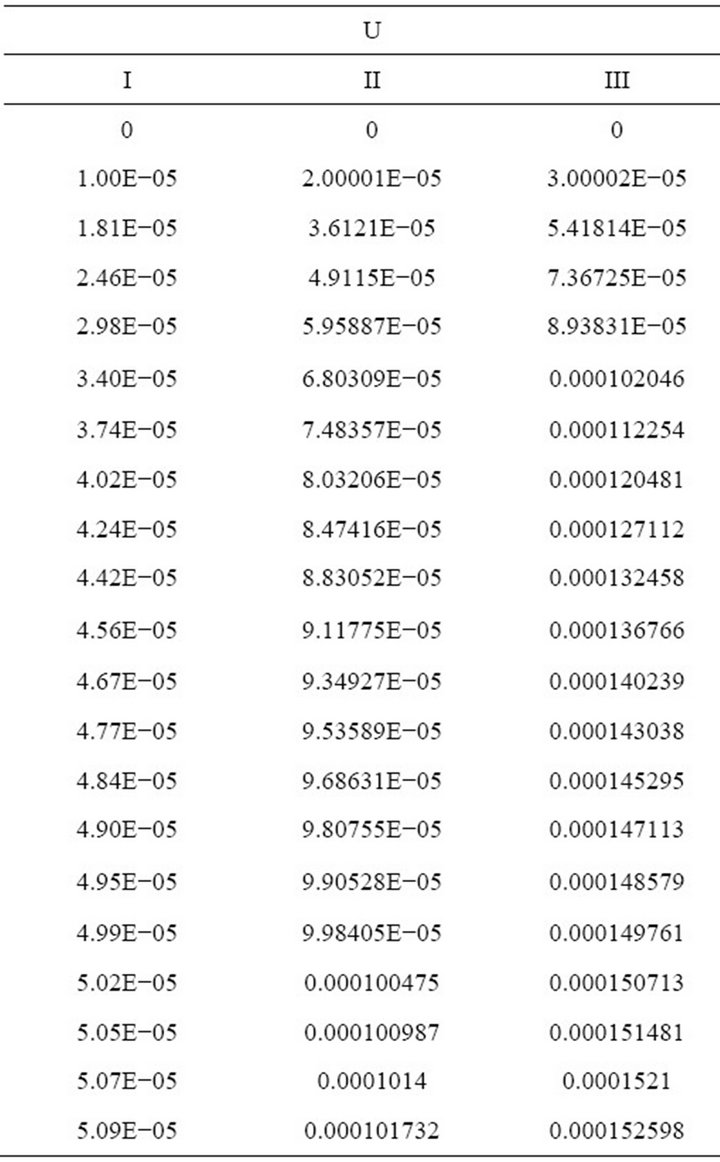


Table 1. Table for primary velocity.

Figure 2. Primary velocity profile.



Table 2. Table for secondary velocity.

Figure 3. Secondary velocity profile.



Table 3. Table for temperature.

Figure 4. Temperature distribution.
from the plate temperature profiles begin to increase uniformly with increase in joules parameter before they resume constant distribution very far away from the plate.
5. Discussion of the Results
An increase in the Joules parameter R increases the secondary velocity and temperature profiles uniformly after some distance from the plate, but as the distance tends far away from the plate the curves exhibit constant velocity and temperature profile distributions as shown in the curves above. While in the case of primary velocity profiles, the velocity increases rapidly with an increase in Joule parameter is very close to the plate and exhibits constant profiles distribution far away from the plate as shown in Figure 2.
6. Conclusions
Analysis of the effects of various Joule parameters on the velocities and temperature distribution on unsteady free convection incompressible fluid flow past an infinite vertical porous flat plate has been carried out. In all the cases considered, the velocity was resolved into two components and temperature in one component, our work was restricted to the laminar boundary layer.
The results for  when the temperature of the plate is greater than that of the fluid in the free stream region, which implies that the heat will be transferred from the plate to the fluid which refers to cooling of the plate by free convection currents.
when the temperature of the plate is greater than that of the fluid in the free stream region, which implies that the heat will be transferred from the plate to the fluid which refers to cooling of the plate by free convection currents.
We found that an increase in Joule parameter number leads to an increase in velocity and temperature is uniformly distributed near the plate, but away from the plate, the velocity and temperature profiles remain constantly distributed. This reveals that the overall heat transfer in MHD free convective fluid flow depends on the strength of Joule heating and decreases with an increase in Joule heating parameter and that the lowest average temperature in the flow field is obtained for 
REFERENCES
- M. Faraday, “Electricity Researches in Electricity,” 1st Series Philosophical Transactions of the Royal Society, 1831, pp. 125-162.
- L. Calvert and C. Santos, “Research Article on the Fundamental Principle of MHD,” Applied Mathematics and Computation, Vol. 108, 2002, pp. 11-21.
- G. S. Ramulu and S. K. Ghosh, “Effect of Hall Current on MHD Flow and Heat Transfer a Long a Porous Flat Plate with Mass Transfer,” International Journal for Engineering Science, Vol. 24, No. 7, 2007, pp. 1183-1193.
- I. C. Cooker and O. Mubo-Pepple, “Influence of Viscous Dissipation and Radiation on Unsteady MHD Free-Convection Flow past an Infinite Heated Vertical Plate in a Porous Medium with Time Independent Suction,” International Journal of Heat and Mass Transfer, Vol. 46, No. 13, 2003, pp. 2305-2311. doi:10.1016/S0017-9310(02)00544-6
- J. Jordan, “Network Simulation Method to Radiation and Viscous Dissipation Effect on MHD Unsteady Free Convection over Vertical Porous Plate,” Applied Mathematics Modeling, Vol. 31, No. 9, 2007, pp. 2019-2033. doi:10.1016/j.apm.2006.08.004
- M. E. Abo-Eldahab and A. M. El Aziz, “Viscous Dissipation and Joule Heating Effects on MHD Free Convection from a Vertical Plate with Power-Law Variation in Surface Temperature in the Presence of Hall and Ion-Slip Currents,” Applied Mathematical Modeling, Vol. 29, No. 6, 2005, pp. 579-595. doi:10.1016/j.apm.2004.10.005
- M. Kinyanjui and N. Chaturvedi, “MHD Stokes Problem for a Vertical Infinite Plate in a Dissipative Rotating Fluid with a Hall Current,” Energy Conversion and Management, Vol. 39, No. 5-6, 1998, pp. 541-548. doi:10.1016/S0196-8904(96)00107-0
- G. C. Duwahiri and D. P. Das, “Viscous and Joule Heating Effect on Forced Convection Flow of Ionized Gases along a Plane Wall with Periodic Suction and Heat Source, Model,” Simulation and Control B, Vol. 27, No. 2, 2005, pp. 47-55.

