Intelligent Control and Automation
Vol. 4 No. 1 (2013) , Article ID: 27846 , 7 pages DOI:10.4236/ica.2013.41011
Estimation of Sensitivity of the DS/AHP Method While Solving Foresight Problems with Incomplete Data
Institute for Applied Systems Analysis, National Technical University of Ukraine “Kyiv Polytechnic Institute”, Kyiv, Ukraine
Email: natalidmp@gmail.com, n.nedashkivska@gmail.com
Received September 20, 2012; revised October 20, 2012; accepted October 28, 2012
Keywords: Analytic Hierarchy Process; Dempster-Shafer Theory; Incomplete Expert Information; Multiple Criteria Analysis; Combination Rules; Rank Reversal; Foresight Problems
ABSTRACT
The paper provides mathematical analysis of sensitivity of different combination rules in the DS/AHP method when an alternative is added to the set of decision alternatives while solving foresight problems. Different cases of rank reversals are defined and two sets of conditions for these cases using the method DS/AHP are considered. Rank reversals are illustrated when the DS/AHP method is used to solve practical problem of critical technologies of energy conservation and power efficiency evaluation in Ukraine. It is shown that the DS/AHP method is not sensitive to exclusion (or addition) of an irrelevant decision alternative from (or to) the set of decision alternatives.
1. Introduction
Technological foresight is a decision making relative to complex systems with human factor concerning their potential behavior in future [1]. Foresight problems have innovation character. Mainly information of qualitative character in a form of expert estimates, which is often incomplete, fuzzy and contradictory, serves as input data for these problems. Therefore, technique of decisionmaking support must include methods for processing information of the mentioned character and also means of estimation of sensitivity and validity for the obtained results.
One of the methods, which are applied in the technique of scenario analysis [1] for solving problems of technological foresight, is the Analytic Hierarchy Process (AHP). Elaborated by T. Saaty AHP and its generalization the Analytic Network Process are popular decision tools used to weight items based on pairwise comparisons in terms of multiple criteria [2-5]. Nowadays AHP and its extensions are used to determine relative weights of items and probabilities of scenarios for solving foresight problems [6,7].
While solving foresight problems, information about decision alternatives may be incomplete due to time limitations, ignorance, intangible nature of some attributes, limited information processing capabilities etc. Besides, a decision maker is not always able to make pairwise comparisons between all decision alternatives. However, this is a prerequisite for the application of AHP. The DS/AHP method [8,9], which incorporates AHP with the Dempster-Shafer theory (DST) of evidence [10] solves a multiple-criteria decision-making (MCDM) problem directly based on its incomplete expert judgments in terms of criteria. Different combination rules in DST represent different treatment of conflict in the aggregated result.
One of the problems associated with the use of MCDM techniques is the possibility to change the ranking of decision alternatives when an alternative is added or deleted (the rank reversal). A detailed discussion on different types of rank reversals in the AHP method will be found in the literature of the subject [11-16]. Some rank reversal cases also occur when other MCDM methods, in particular the ELECTRE II, III, the TOPSIS methods and others, are used [17,18]. Several numerical examples are given to validate the DS/AHP method with respect to the Pareto optimality and the independence of irrelevant decision alternatives [19].
This paper provides mathematical analysis and simulation study of sensitivity of different combination rules of the DS/AHP method when an alternative is added to the set of decision alternatives while solving foresight problems.
2. The DS/AHP Method and the Combination Rules
The Dempster-Shafer theory (DST) can be regarded as an extension of the Bayesian theory that can deal with incomplete data. To combine aspects of DST and AHP the DS/AHP method of MCDM is introduced [8]. DS/AHP (as in AHP) is based on a hierarchical structure of a problem.
In DS/AHP measures of probability are assigned to groups of decision alternatives (DAs), each group of identified DAs is compared to the frame of discernment  (all possible DAs), and expert expresses some degree of “favorable knowledge” on each of these groups. This differs from AHP, which makes pairwise comparisons between individual DAs. Number of identified groups reflects the amount of knowledge the expert has on a criterion. Let us consider steps of the DS/AHP method (Figure 1):
(all possible DAs), and expert expresses some degree of “favorable knowledge” on each of these groups. This differs from AHP, which makes pairwise comparisons between individual DAs. Number of identified groups reflects the amount of knowledge the expert has on a criterion. Let us consider steps of the DS/AHP method (Figure 1):
Step 1: to find criteria priority values (CPVs) using the standard eigenvector method of AHP.
Step 2: to identify groups of DAs for each criterion. The number of identified groups is decided by the expert and may reflect the amount of knowledge the expert has on the criterion. Within one group, DAs have equal favorability to the frame of discernment .
.
Step 3: to construct the knowledge matrix
 for each criterion where
for each criterion where
 ,
,  , values
, values  are the measures of favorability of the groups of DAs
are the measures of favorability of the groups of DAs 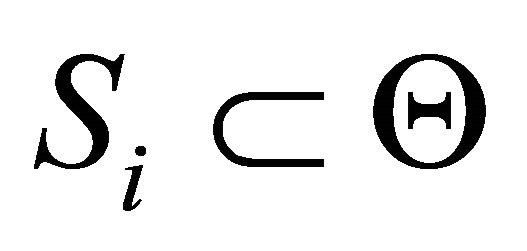 with respect to
with respect to  in terms of the criterion,
in terms of the criterion,  is the CPV;
is the CPV; ,
, ;
;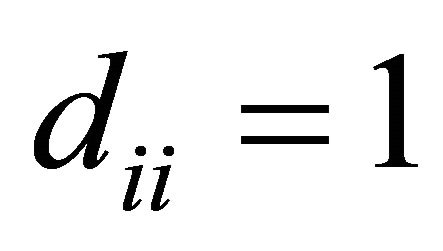 ,
,  for
for ,
, ; r-number of groups of DAs on the criterion.
; r-number of groups of DAs on the criterion.
Step 4: to calculate the associated sets of priority values for the knowledge matrices for each criterion (basic probability assignment (bpa) structures for groups of

Figure 1. Steps of the DS/AHP method.
DAs and  in terms of the criteria) again using the standard eigenvector method of AHP. Analytic functions
in terms of the criteria) again using the standard eigenvector method of AHP. Analytic functions  are constructed to find the bpa [9]:
are constructed to find the bpa [9]:
 ,
,  ,
, 

Step 5: to aggregate the bpa structures founded in step 4 into a single bpa  using a rule of combination, where p is a number of decision criteria. The resulting bpa structure represents the amounts of exact belief in groups of DAs based on the combined evidence from all the criteria.
using a rule of combination, where p is a number of decision criteria. The resulting bpa structure represents the amounts of exact belief in groups of DAs based on the combined evidence from all the criteria. 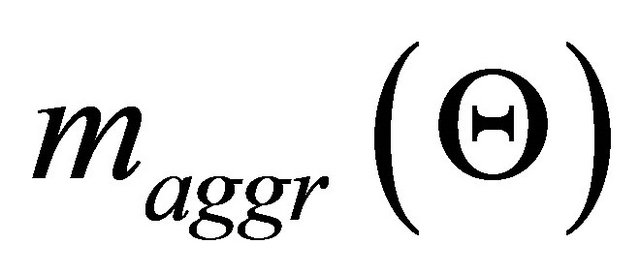 is the value of combined uncertainty.
is the value of combined uncertainty.
Step 6: to calculate values of the belief
 and plausibility
and plausibility 
functions and obtain the belief interval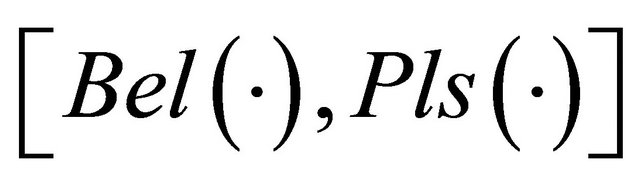 :
:
 ,
,

for each group of DAs .
.
There are different ways where evidence can be combined in DST. The original Dempster’s rule of combination is considered as AND-operation and ignores the conflict between the evidence. In the DS/AHP method proposed in [8,9] the Dempster’s rule is used instead of distributive and ideal modes of AHP to combine the measures of evidence (bpa values) from different sources (decision criteria). This rule assumes that these sources are independent. According to the rule combined evidence from all criteria is defined by the function  , which is a bpa:
, which is a bpa:

if 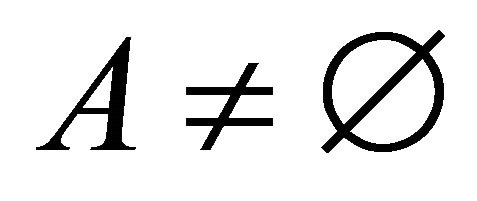 and
and , where m1, m2 are bpa structures to be aggregated,
, where m1, m2 are bpa structures to be aggregated,  are focal elements, the normalization factor
are focal elements, the normalization factor

is interpreted as a measure of conflict between the pieces of evidence.
Other combination rules represent different treatment of conflict in the aggregated result. The Yager’s rule of combination is as follows [20]:

In the rule there is any normalization factor. To represent the conflict the value 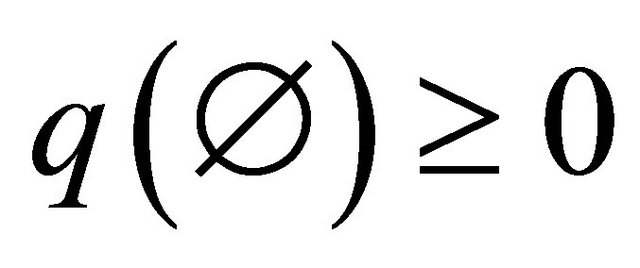 is used. This conflict value is added to the aggregated probability assignment of the frame, i.e. conflict is attributed to the frame and the evidence is not changed through the normalization.
is used. This conflict value is added to the aggregated probability assignment of the frame, i.e. conflict is attributed to the frame and the evidence is not changed through the normalization.
In the Zhang’s combination rule the intersection of focal elements is considered as follows [21]:

where |.| defines a cardinality of a set, K is a normalization factor to provide the sum of the  to add to 1.
to add to 1.
The Dubois and Prade’s combination rule is ORbased and therefore any normalization is required [22]:
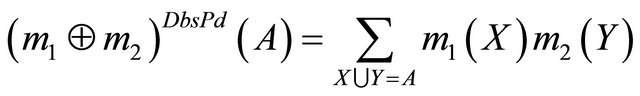 If all sources of evidence are reliable, an AND-based operation is appropriate. If only one source is considered reliable, an OR-based operation has to be used.
If all sources of evidence are reliable, an AND-based operation is appropriate. If only one source is considered reliable, an OR-based operation has to be used.
The described Yager’s, Zhang’s, Dubois and Prade’s rules represent modified Dempster’s rule. Other combination rules are based on a weighted average function. The discount average combination rule is as follows [10]:
 where the
where the ’s are degrees of trust in the belief functions
’s are degrees of trust in the belief functions ’s to be aggregated,
’s to be aggregated, . The rule is used when all belief functions are highly conflicting and also to eliminate the influence of single strongly conflicting belief function.
. The rule is used when all belief functions are highly conflicting and also to eliminate the influence of single strongly conflicting belief function.
Also the simple average combination rule which may be considered as the distributive synthesis mode is used:
 where the
where the ’s are degrees of trust in the sources,
’s are degrees of trust in the sources, ’s are the bpa’s for the belief structures to be aggregated,
’s are the bpa’s for the belief structures to be aggregated, .
.
A combination rule has to aggregate evidence obtained from more than two sources (decision criteria). All of the above rules are commutative. The Dempster’s, Dubois and Prade’s and average rules are associative. The Yager’s rule is quasi-associative.
One of the problems with a MСDM technique is a possibility to change the ranking of DAs when a DA is added or deleted (so called rank reversal). In the next Section the estimation of sensitivity of the above combination rules while adding a DA is provided.
3. Estimation of Sensitivity of the DS/AHP Method
Suppose n DAs A1, A2,∙∙∙, An are evaluated in terms of two decision criteria C1 and C2. For these criteria d1 and d2 groups of DAs S11, S12,∙∙∙,  and S21, S22,∙∙∙,
and S21, S22,∙∙∙,  , respectively, are identified as being comparable to the frame of discernment
, respectively, are identified as being comparable to the frame of discernment , where
, where ,
,  ,
,  ,
, . Using the DS/AHP method, the belief measures
. Using the DS/AHP method, the belief measures  and belief intervals
and belief intervals  are calculated for each group of DAs and the frame
are calculated for each group of DAs and the frame .
.
We are interested in the conditions of changes in the DA ranking orders obtained by the DS/AHP method when a DA is added to the set of DAs. Two sets of such conditions are defined [23]. The first set of conditions deals with the changes in the belief-based ranking orders of DAs. Belief measures  and
and  denote the amounts of exact belief in a group
denote the amounts of exact belief in a group  based on combined evidence from two criteria before and after a DA is added to the set of DAs, respectively. The second set of conditions of changes in the DA ranking orders concerns the comparison of belief intervals
based on combined evidence from two criteria before and after a DA is added to the set of DAs, respectively. The second set of conditions of changes in the DA ranking orders concerns the comparison of belief intervals
 and
and , where plausibility measures
, where plausibility measures  and
and  denote the maximum probability of possible support to a group
denote the maximum probability of possible support to a group 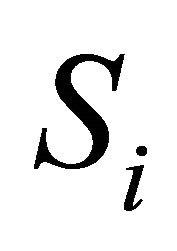 before and after a DA is added to the set of DAs, respectively.
before and after a DA is added to the set of DAs, respectively.
Condition #1 of rank reversal: Preference relation defined by belief measures for groups  and
and  is changed after a DA is added to the set of DAs:
is changed after a DA is added to the set of DAs:

where ,
,

Condition #2 of rank reversal: Preference relation defined by belief intervals for groups  and
and  is changed after a DA is added to the set of DAs.
is changed after a DA is added to the set of DAs.
To obtain the preference relations among groups of DAs the evidential reasoning ranking method is used [23] to generate the rank of groups of DAs based on their belief intervals.
In this paper, three known criteria are used to test sensitivity of the DS/AHP method while adding a DA. These criteria were applied to test other MCDM methods [17].
Test criterion #1: An effective MCDM method should not change the indication of the best DA when an irrelevant DA (that is dominated by one or more previously existing DAs) is added to the set of DAs given that the relative importance of each decision criterion remains unchanged. The same should also be true for the relative rankings of the rest of the unchanged DAs.
Test criterion #2: The rankings of DAs by an effective MCDM method should follow the transitivity property.
Test criterion #3: For the same decision problem and while using the same MCDM method, after combining the rankings of the smaller problems that an MCDM problem is decomposed into, the new overall ranking of the DAs should be identical to the original overall ranking of the un-decomposed problem.
Let us consider different cases of rank reversals when the DS/AHP method is used. Suppose that an irrelevant DA is added to the set of DAs, it will be the most interesting result for solving foresight problems.
Case 1: New DA  is irrelevant and forms a separate group with respect to each one of the decision criteria, i.e.
is irrelevant and forms a separate group with respect to each one of the decision criteria, i.e. 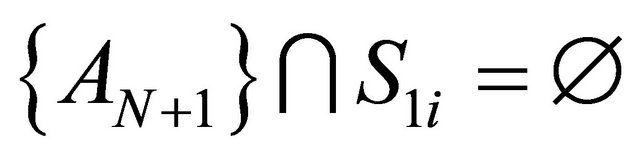 and
and ,
, 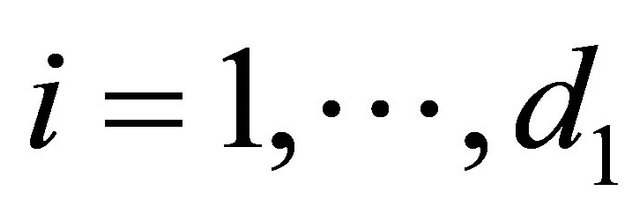 ,
, .
.
The intersections’ sub-matrix  for groups of DAs
for groups of DAs  in the Dempster’s, Yager’s and Zhang’s combination rules remains unchanged when such DA
in the Dempster’s, Yager’s and Zhang’s combination rules remains unchanged when such DA  is added. However, the normalization constants K in the Dempster’s and Zhang’s rules are changed. Therefore the values of aggregated mass function and therefore the corresponding belief measures for groups of DAs
is added. However, the normalization constants K in the Dempster’s and Zhang’s rules are changed. Therefore the values of aggregated mass function and therefore the corresponding belief measures for groups of DAs  may be changed disproportionately when these rules are applied. Thus, rank reversals in the rules may occur under the Condition #1. In the Yager’s combination rule rank reversals do not occur when such new DA is added.
may be changed disproportionately when these rules are applied. Thus, rank reversals in the rules may occur under the Condition #1. In the Yager’s combination rule rank reversals do not occur when such new DA is added.
Case 2: New DA  is irrelevant and forms a separate group in terms of only one decision criterion. In terms of the other decision criterion this DA
is irrelevant and forms a separate group in terms of only one decision criterion. In terms of the other decision criterion this DA  has the same measure of favorability with respect to
has the same measure of favorability with respect to  as one or several previously existing DAs, i.e.
as one or several previously existing DAs, i.e.  is included into one of the existing groups of DAs.
is included into one of the existing groups of DAs.
Let DA 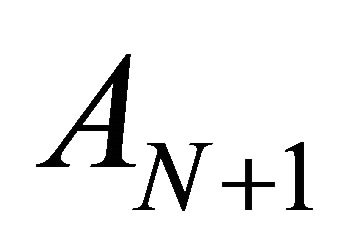 be included into the group
be included into the group 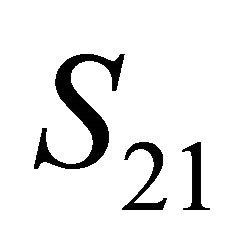 (without loss of generality, the choice of
(without loss of generality, the choice of  is not detrimental). Then, after introduction of the DA
is not detrimental). Then, after introduction of the DA  the groups S11, S12,∙∙∙,
the groups S11, S12,∙∙∙,  and
and  are identified in terms of criterion C1 and the groups
are identified in terms of criterion C1 and the groups  in terms of criterion C2, where
in terms of criterion C2, where . The intersections’ sub-matrix in each of the Dempster’s, Yager’s and Zhang’s combination rules for the groups of “previously existing” DAs is changed, since the intersection of group
. The intersections’ sub-matrix in each of the Dempster’s, Yager’s and Zhang’s combination rules for the groups of “previously existing” DAs is changed, since the intersection of group  with the frame
with the frame  is changed. The normalization constants in the Dempster’s and Zhang’s combination rules are also changed. Therefore, the values of aggregated mass function and therefore the corresponding belief measures for groups of DAs
is changed. The normalization constants in the Dempster’s and Zhang’s combination rules are also changed. Therefore, the values of aggregated mass function and therefore the corresponding belief measures for groups of DAs  may be changed disproportionately when these rules are used. Thus, rank reversal in these rules may occur under the Condition #1.
may be changed disproportionately when these rules are used. Thus, rank reversal in these rules may occur under the Condition #1.
Let us consider the possibility of rank reversal in the DS/AHP method under the test criterion #2. Suppose that the DS/AHP method has ranked a set of DAs of a decision problem. Next, assume that this problem is decomposed into a set of smaller problems each defined on two DAs at a time and the same number of decision criteria as in the original problem. Then, according to the test criterion #2, all the partial rankings deriving from the smaller problems should comply with the transitivity property. Let us denote groups of DAs in terms of two decision criteria C1 and C2 as  and
and . Suppose each of the groups consists of a single element, namely
. Suppose each of the groups consists of a single element, namely . Assume that the groups of DAs are considered in pairs and rankings of two arbitrary pairs are
. Assume that the groups of DAs are considered in pairs and rankings of two arbitrary pairs are  and
and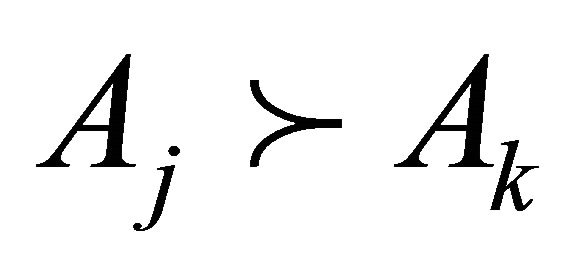 . Then the aggregated mass of DA
. Then the aggregated mass of DA 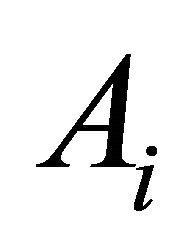 under the Dempster’s combination rule is
under the Dempster’s combination rule is
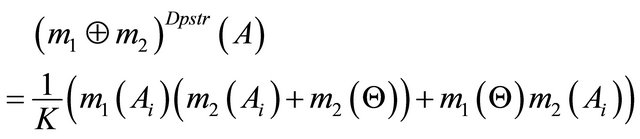 .
.
Then rankings  and
and  lead to the following inequalities:
lead to the following inequalities:


After combination of these inequalities we have . Thus, if each group of DAs consists of a single element, then the transitivity property is satisfied, and, hence, rank reversal does not appear in the Dempster’s combination rule under the test criterion #2. The same conclusion is true for the Yager’s and Zhang’s combination rules.
. Thus, if each group of DAs consists of a single element, then the transitivity property is satisfied, and, hence, rank reversal does not appear in the Dempster’s combination rule under the test criterion #2. The same conclusion is true for the Yager’s and Zhang’s combination rules.
4. Evaluation of Critical Technologies of Energy Conservation and Power Efficiency in Ukraine
The DS/AHP method was used to calculate relative priority values for critical technologies (CTs) of energy conservation and power efficiency in Ukraine. Quantitative information of passports of CTs and qualitative information in a form of expert estimates serves as input data for this problem.
A list of 14 CTs and their technical passports were presented by leading organizations in energy sector of Ukraine on a first stage of foresight process. Then the CTs were clustered as follows: energy conservation CTs, renewable energy CTs and eco-house CT. Energy conservation CTs include energy conservation while producing energy (cogeneration technologies and power machine building) and in energy networks (electrical power engineering and technologies of burning). Renewable energy CTs include geothermal, wind, solar and bioenergetics technologies. Problem of power efficiency is included in a notion of eco-house only as a part along with building materials production, construction of ecohouse and waste utilization. Therefore the technology of effective eco-house was considered separately. Relative priority values for the 14 CTs A1 - A14 were calculated using the DS/AHP method on basis of information of passports of the CTs and expert judgments about relative importance of CTs in terms of risk factors and relative importance of decision criteria.
Groups of DAs were as follows:
- In terms of criterion C1: S1 = {A1, A2, A5, A6, A12}, S2 = {A3, A8, A9, A10, A13}, S3 = {A7, A11}, S4 = {A4}- In terms of criterion C2: S1 = {A11, A12, A13}, S2 = {A6, A10}, S3 = {A2, A3}, S4={A4, A7, A8, A9}, S5 = {A1, A5}- In terms of criterion C3: S1 = {A12}, S2 = {A11, A13}, S3 = {A6, A7}, S4 = {A3, A4, A5}, S5 = {A1, A2, A8, A9, A10}- In terms of criterion C4: S1 = {A3}, S2 = {A1, A2, A4, A8, A9, A10, A11, A12}, S3 = { A5, A6, A7, A13}.
CPVs of the criteria were equal to 0.3, 0.3, 0.2 and 0.2.
Measures of favorability  of the groups of DAs with respect to
of the groups of DAs with respect to  and bpa structures of the groups of DAs in terms of criteria are illustrated in Table 1.
and bpa structures of the groups of DAs in terms of criteria are illustrated in Table 1.
Next step is to aggregate the bpa structures into a single bpa . For example, an aggregated bpa structure
. For example, an aggregated bpa structure  using the Dempster’s combination rule is as follows:
using the Dempster’s combination rule is as follows:
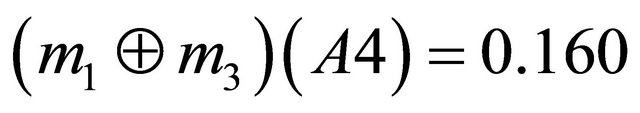 ,
, ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

Table 1. Measures of favorability di and bpa structures of the groups of DAs in terms of decision criteria C1 (a), C2 (b), C2 (c) and C4 (d).

 ,
,
 ,
,  ,
,
 .
.
As a result, based on the aggregated bpa structure  ranking of the CTs was constructed. CTs with the highest priorities are presented in Table 2.
ranking of the CTs was constructed. CTs with the highest priorities are presented in Table 2.
Exclusion from consideration priority DA may lead to significant changes of results. Thus, exclusion of DA No3 “Technology of steam compressor thermal pumps” which is in a group of optimal DAs in terms of one of the criteria, results in redistribution of priority rating and DA “Technology of synthetic fuel (gas) production” receives 4th rank. Exclusion of DA of lower rank, which is less priority, in fact has no influence on the solution.
5. Conclusions
In the paper it is shown that the applications of Dempster’s, Zhang’s and average combination rules of the DS/AHP method may lead to well-known phenomenon of rank reversal. Rank reversal is a changing in overall ranks of decision alternatives when adding or excluding a decision alternative. Of particular interest are changings in these ranks when adding or excluding a decision alternative, which is irrelevant, i.e. nonoptimal in terms of
Table 2. Priorities and ranks of the energy conservation and power efficiency CTs.

each decision criterion, and as a result overall less priority. Our investigation reveals that exclusion of such decision alternative while solving foresight problems with incomplete data using the DS/AHP method does not result in redistributions in a subset of high priority decision alternatives and, therefore has no influence on the choice of high priority solution. Thus, the DS/AHP method is not sensitive to exclusion (or addition) of an irrelevant decision alternative from (or to) the set of decision alternatives.
It is the very first time that the DS/AHP method is used to solve foresight problems, as well as rank reversals are reported to occur while using this method. Therefore, determination of priority critical technologies a priori requires additional investigations concerning possibility of rank reversals when a decision alternative is added or excluded.
REFERENCES
- M. Z. Zgurovsky and N. D. Pankratova, “System Analysis: Theory and Applications,” Springer, Berlin, 2007.
- T. L. Saaty, “The Analytic Hierarchy Process,” McGrawHill, New York, 1980.
- T. L. Saaty, “Theory of the Analytic Hierarchy Process, Part 2.1,” System Research & Information Technologies, No. 1, 2003, pp. 48-72.
- T. L. Saaty, “Theory of the Analytic Hierarchy and Analytic Network Processes—Examples, Part 2.2,” System Research & Information Technologies, No. 2, 2003, pp. 7-34.
- T. L. Saaty, “The Analytic Network Process, Examples, Part 2.3,” System Research & Information Technologies, No. 4, 2003, pp. 7-23.
- N. D. Pankratova and N. I. Nedashkovskaya, “Method for Processing Fuzzy Expert Information in Prediction Problems. Part I,” Journal of Automation and Information Sciences, Vol. 39, No. 3, 2007, pp. 22-36. doi:10.1615/JAutomatInfScien.v39.i4.30
- N. D. Pankratova and N. I. Nedashkovskaya, “Method for Processing Fuzzy Expert Information in Prediction Problems. Part II,” Journal of Automation and Information Sciences, Vol. 39, No. 6, 2007, pp. 30-44. doi:10.1615/JAutomatInfScien.v39.i6.20
- M. J. Beynon, B. Curry and P. H. Morgan, “The Dempster-Shafer Theory of Evidence: An Alternative Approach to Multicriteria Decision Modeling,” Omega, Vol. 28, No. 1, 2000, pp. 37-50. doi:10.1016/S0305-0483(99)00033-X
- M. J. Beynon, “DS/AHP Method: A Mathematical Analysis, Including an Understanding of Uncertainty,” European Journal of Operational Research, Vol. 140, No. 1, 2002, pp. 148-164. doi:10.1016/S0377-2217(01)00230-2
- G. Shafer, “A Mathematical Theory of Evidence,” Princeton University Press, Princeton, 1976.
- J. Barzilai and F. A. Lootsma, “Power Relations and Group Aggregation in Multiplicative AHP and SMART,” Proceedings of the 3rd International Symposium on the AHP, Washington DC, 1994, pp. 157-168.
- V. Belton and T. Gear, “On a Shortcoming of Saaty’s Method of Analytic Hierarchies,” Omega, Vol. 11, No. 3, 1983, pp. 228-230. doi:10.1016/0305-0483(83)90047-6
- J. S. Dyer, “Remarks on the Analytic Hierarchy Process,” Management Science, Vol. 36, No. 3, 1990, pp. 249-258. doi:10.1287/mnsc.36.3.249
- E. Triantaphyllou, “Two New Cases of Rank Reversals When the AHP and Some of Its Additive Variants Are Used That Do Not Occur with the Multiplicative AHP,” Journal of Multi-Criteria Decision Analysis, Vol. 10, No. 1, 2001, pp. 11-25. doi:10.1002/mcda.284
- T. L. Saaty, “Rank Generation, Preservation and Reversal in the Analytic Hierarchy Process,” Decision Sciences, Vol. 18, No. 2, 1987, pp. 157-177. doi:10.1111/j.1540-5915.1987.tb01514.x
- T. L. Saaty, “Rank from Comparisons and from Ratings in the Analytic Hierarchy/ Network Processes,” European Journal of Operational Research, Vol. 168, No. 2, 2006, pp. 557-570. doi:10.1016/j.ejor.2004.04.032
- X. Wang and E. Triantaphyllou, “Ranking Irregularities When Evaluating Alternatives by Using Some ELECTRE Methods,” Omega, Vol. 36, No. 1, 2008, pp. 45-63. doi:10.1016/j.omega.2005.12.003
- V. G. Totsenko, “On Problem of Reversal of Alternatives Ranks While Multicriteria Estimating,” Journal of Automation and Information Sciences, Vol. 38, No. 6, 2006, pp. 1-11. doi:10.1615/J Automat Inf Scien.v38.i6.10
- M. J. Beynon, “The Role of the DS/AHP in Identifying Inter-Group Alliances and Majority Rule within Group Decision Making,” Group Decision and Negotiation, Vol. 15, No. 1, 2006, pp. 21-42. doi:10.1007/s10726-005-1159-9
- R. Yager, “On the Dempster-Shafer Framework and New Combination Rules,” Information Sciences, Vol. 41, No. 2, 1987, pp. 93-137. doi:10.1016/0020-0255(87)90007-7
- L. Zhang, “Representation, Independence, and Combination of Evidence in the Dempster-Shafer Theory,” In: R. R. Yager, J. Kacprzyk and M. Fedrizzi, Eds., Advances in the Dempster-Shafer Theory of Evidence, John Wiley & Sons, Inc., New York, 1994, pp. 51-69.
- D. Dubois and H. Prade, “A Set-Theoretic View on Belief Functions: Logical Operations and Approximations by Fuzzy Sets,” International Journal of General Systems, Vol. 12, No. 3, 1986, pp. 193-226. doi:10.1080/03081078608934937
- N. I. Nedashkovskaya, “Multi-Criteria Decision Making in the Presence of Ignorance Using the DS/AHP Method,” Proceedings of the 11th International Symposium for the AHP/ANP (ISAHP), Naples, 15-18 June 2011. http://www.isahp.org/italy2011/proceedings-from-past-meetings

