Journal of Modern Physics
Vol.3 No.6(2012), Article ID:20193,5 pages DOI:10.4236/jmp.2012.36069
A New Narrowband Phase Modulation Mathematical Identity
Department of Physics, Jordan University of Science and Technology, Irbid, Jordan
Email: saadeh@just.edu.jo
Received January 27, 2012; revised April 15, 2012; accepted April 28, 2012
Keywords: Phase Modulation; Bessel Functions; Optical Communication
ABSTRACT
A new mathematical identity is suggested to describe narrow band phase modulation and other similar physical problems instead of using the Bessel function. Bessel functions are extensively used in mathematical physics [1,2], electromagnetic wave propagation and scattering [3,4], and communication system theory [3,5,6]. Such phenomena must often be approximated by appropriate formulas since there is no closed form solution or expression, which usually leads to complex mathematical solutions [5,7]. Comparisons are made between the exact solution numerically calculated and graphed with the new mathematical identities’ prediction of phase modulation behavior. The proposed mathematical identity matches the results very well, leading to simpler analysis of such physical behavior.
1. Introduction
Frequency or phase modulation is an efficient form of communication, where information is transmitted over a carrier signal by changing the instantaneous frequency [4]. Phase modulation has been heavily employed over the last century, and is the bases of all modern digital communication systems. Bessel functions are used to better describe the mathematical equations that govern phase modulation.
The expressions and
and  where δ and ωm are the index and frequency of modulation, appear frequently in physics research and literature. They play a key role in the mathematical treatment of narrowband frequency modulation in communication and in antennas radiation analysis, design and studies [3,4].
where δ and ωm are the index and frequency of modulation, appear frequently in physics research and literature. They play a key role in the mathematical treatment of narrowband frequency modulation in communication and in antennas radiation analysis, design and studies [3,4].
Usually  and
and 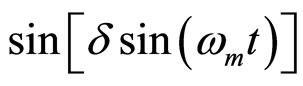 are replaced by Bessel function series, which adds complexity to the mathematical treatment. In many cases this can lead to using mathematical approximations that reduce the accuracy of the analysis.
are replaced by Bessel function series, which adds complexity to the mathematical treatment. In many cases this can lead to using mathematical approximations that reduce the accuracy of the analysis.
Previous published work done in collaboration with Prof. Salamo from the University of Arkansas dealt with laser beam propagation through two level samples [8]. While trying to better understanding the evolution of an electric field envelope as the previously studied laser beam propagated through the two level sample, and the effects of phase modulation by using custom in house developed software for a numerical based computer simulation study, it was observed that at a certain beer’s absorption length inside the sample, the electric field envelope looks like an analytical function. During fitting trials of the observed electric field in several trigonometric form functions, an expression for the 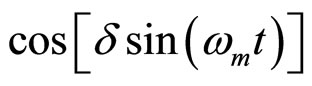 function in two terms was developed, and the idea of a alterative to the complex Bessel Functions approach was conceived [9-11]. This new expression was compared to the exact
function in two terms was developed, and the idea of a alterative to the complex Bessel Functions approach was conceived [9-11]. This new expression was compared to the exact , the agreement and fit are excellent for δ < 1 i.e. for small index of modulation, which is the case in optical frequency modulation and in communications.
, the agreement and fit are excellent for δ < 1 i.e. for small index of modulation, which is the case in optical frequency modulation and in communications.
2. Mathematical Development
Our first postulate is:
 (1)
(1)
To verify the accuracy of our assumption, the end result undergoes vigorous numerical and analytical testing.
If the proposed postulate is true then it follows:
 (2)
(2)
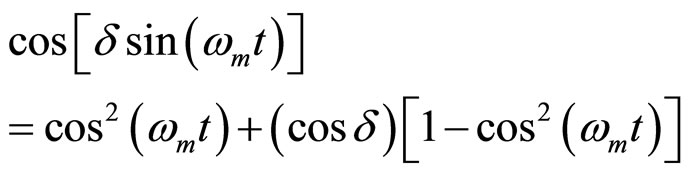 (3)
(3)
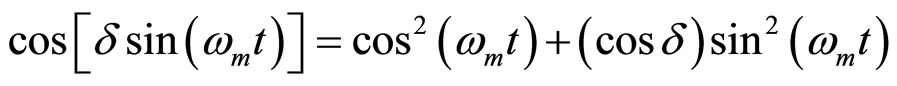 (4)
(4)
 (5)
(5)
by substituting equation (4) in equation (5),
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
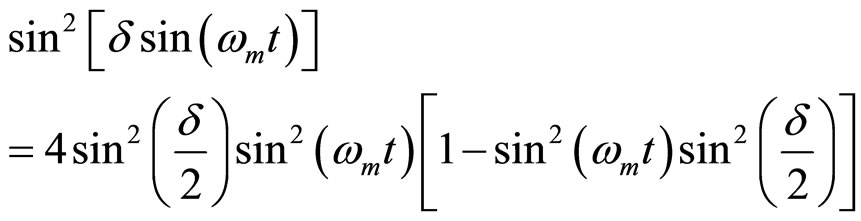 (11)
(11)
 (12)
(12)
The second postulate is:
 (13)
(13)
If this is a valid assumption, then:
 (14)
(14)
 (15)
(15)
 (16)
(16)
If that is right then:
 (17)
(17)
by substituting equation (16) in equation (17),
 (18)
(18)
 (19)
(19)
 (20)
(20)
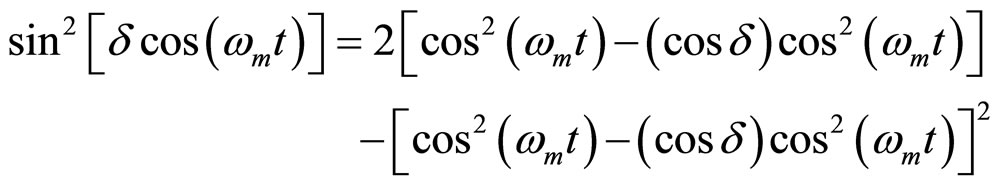 (21)
(21)
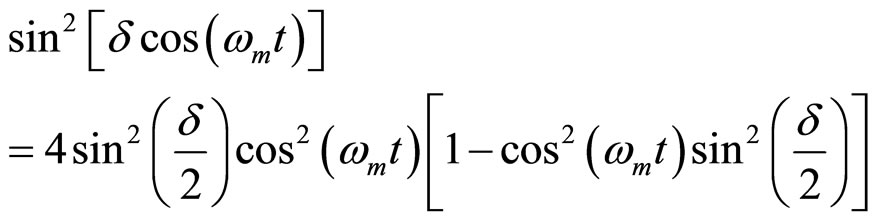 (22)
(22)
 (23)
(23)
From the above derivation, we get our new identities in equations (4), (12), (16) and (23).
3. Testing the Suggested Expression
The new expression is tested in two approaches. The first approach is to analytically compare the result to the established phase modulation of light [12]. The second approach to compare the results with computer simulations.
3.1. Phase Modulation of Light
Amnon Yariv discuses phase modulation of light in chapter 9 of his book Introduction to Optical Electronics [12]. The electric field for the modulated light is given by:
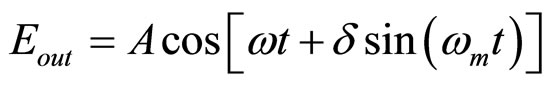 (24)
(24)
where d is the phase modulation index and ωm is the phase modulation frequency.
 (25)
(25)
The above book uses the Bessel function identities
 (26)
(26)
 (27)
(27)
 (28)
(28)
However, it is generally assumed that only the first three terms are significant. This agrees with our experiments in which only the first three terms in the series are detected.
For small modulation, i.e. d < 1, J0(d) = 1 and J1(d) = sin(d/2) which leads to:
 (29)
(29)
If we use our suggested approximation instead of the Bessel function identities in Eout, then:
 (30)
(30)
By using the new identities of equations (4) and (12) in equation (30), we get:
 (31)
(31)
 (32)
(32)
To check this formula against the previous formula of Eout we apply it for small δ where, cosδ = 1 and sin2(d/2) = 0. In this case,
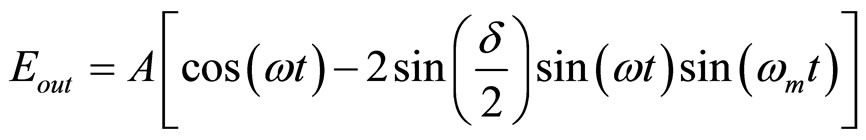 (33)
(33)
If we use the identity:
 (34)
(34)
we get
 (a)
(a)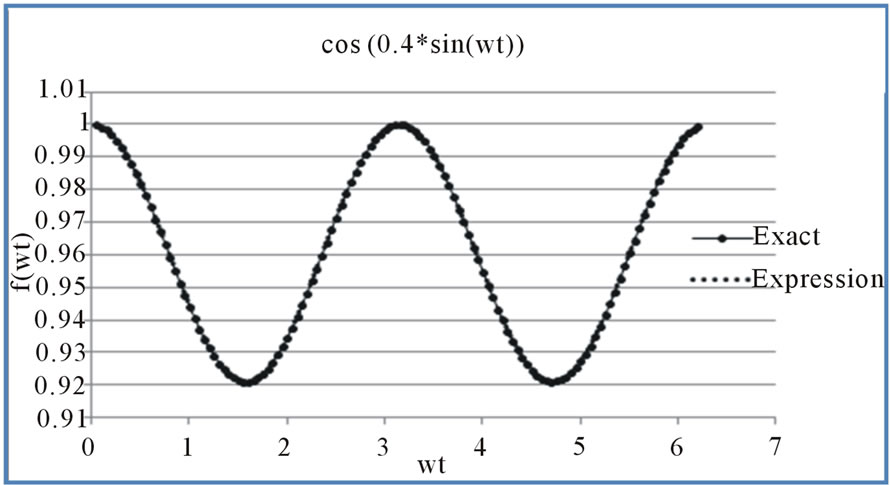 (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 1. Comparison between exact results and proposed expression for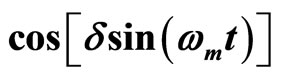 .
.
 (a)
(a) (b)
(b)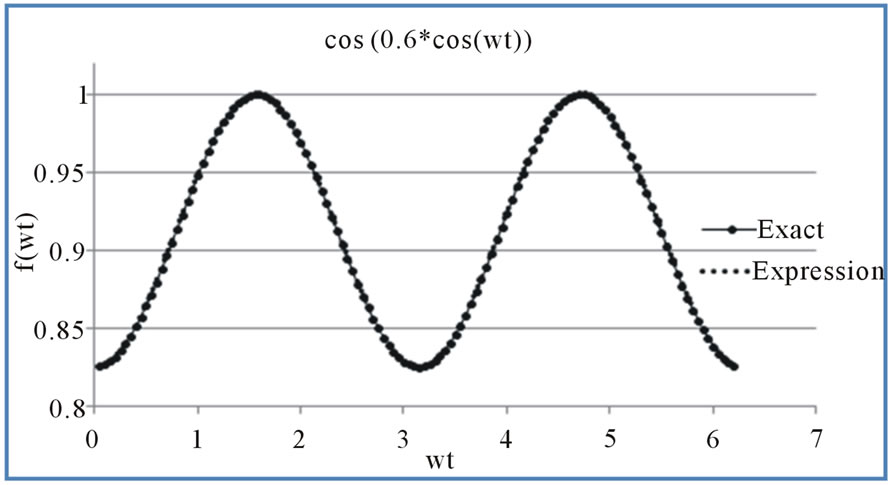 (c)
(c) (d)
(d) (e)
(e)
Figure 2. Comparison between exact results and proposed expression for .
.
 (35)
(35)
Which exactly matches the proposed solution?
3.2. Computer Generated Numerical Comparison
The graphs of Figure 1, compare the computer generated numerical results for the exact equation:  at different values of d with that of the new proposed mathematical identity. Figure 2 shows the comparison for
at different values of d with that of the new proposed mathematical identity. Figure 2 shows the comparison for .
.
4. Conclusion
The derivation of the four new mathematical identities in equations (4), (12), (16) and (23) that describe narrow band phase modulation is presented. The proposed identity can also be used for similar physical phenomena’s that use the Bessel function. The mathematical identity was shown to match analytical and numerical results very well. The new identities greatly reduce computation time and complexity of analytical treatment of such physical behavior.
REFERENCES
- A. V. Alekseev and N. V. Sushilov, “Analytic Solutions of Bloch and Maxwell-Bloch Equations in the Case of Arbitrary Field Amplitude and Phase Modulation” Physical Review A, Vol. 46, No. 1, 1992, pp. 351-355. doi:10.1103/PhysRevA.46.351
- N. Nayak and G. S. Agarwal, “Absorption and Fluorescence in Frequency-Modulated Fields under Conditions of Strong Modulation and Saturation” Physical Review A, Vol. 31, No. 5, 1985, pp. 3175-3182. doi:10.1103/PhysRevA.31.3175
- A. Hund, “Frequency Modulation,” McGraw-Hill, New York, 1942.
- J. D. Jackson, “Classical Electrodynamics,” 3rd edition, Wiley, New York, 1998.
- J. G. Proakis and M. Salehi, “Communication Systems Engineering,” Prentice Hall, Upper Saddle River, 2001.
- N. M. Blachman, “Noise and Its Effect on Communication,” 2nd Edition, Krieger Publishing Co., Malabar, 1982.
- G. N. Watson, “A Treatise on the Theory of Bessel Functions,” 2nd edition, Cambridge University Press, Cambridge, 1995.
- S. Saadeh, J. Shultz and G. Salamo, “Experimental Observation of Chirped Continuous Pulse-train Soliton Solutions to the Maxwell-Bloch Equations,” Optics Express, Vol. 8, No. 2, 2001, pp. 153-158. doi:10.1364/OE.8.000153
- L. A. Pipes, “Applied Mathematics for Engineers and Physicists,” 2nd Edition, McGraw-Hill, New York, 1958.
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” National Bureau of Standards, Washington DC, 1964.
- N. M. Blachman and S. H. Mousavinezhad, “Trigonometric Approximation for Bessel Functions,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 22, No. 1, 1986, pp. 2-7. doi:10.1109/TAES.1986.310686
- A. Yarvis, “Introduction to Optical Electronics,” 2nd Edition, Holt McDougal, Geneva, 1977.

