Open Journal of Fluid Dynamics
Vol.05 No.02(2015), Article ID:57344,8 pages
10.4236/ojfd.2015.52022
Numerical Study of the Influence of Elements inside the Wheelhouse on the Passenger Vehicle Aerodynamic
Edvaldo Angelo1, Gabriel Angelo2,3, Pedro Henrique Di Giovanni Santos3, Delvonei Alves de Andrade3
1Grupo de Simulação Numérica (GSN), Universidade Presbiteriana Mackenzie, São Paulo, Brazil
2Department of Mechanical Engineering, Centro Universitário da Fundação Educacional Inaciana Padre Sabóia de Medeiros (FEI), São Bernardo do Campo, Brazil
3Instituto de Pesquisas Energéticas e Nucleares, IPEN CNEN/SP, Universidade de São Paulo, São Paulo, Brazil
Email: eangelo@mackenzie.br, gangelo@fei.edu.br, pedro_digiovanni_s@hotmail.com, delvonei@ipen.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 May 2015; accepted 21 June 2015; published 24 June 2015
ABSTRACT
Models for the study of computational fluid dynamics in vehicles to determine aerodynamic loads usually take into account only the geometry of the body. Several constructive elements such as the wheel geometry or suspension components are disregarded in the computational models. This work presents the study of the aerodynamics of a one-fourth model passenger vehicle, which contains the wheelhouse interior elements. The goal is to identify the aerodynamic loads produced by these components and their effect on the flow dynamics. Wheel and tire set, brake components, suspension and drive shaft are contemplated. Computer simulations were performed to the vehicle speed varying from 0 to 120 km/h and included the rotation of the tire and wheel assembly, considering the tire geometry in dynamic conditions. The computational model is solved by the finite volume method, wherein the computational domain is divided into tetrahedral and hexahedral elements. The turbulence model used is the standard k − ε.
Keywords:
Computational Fluid Dynamics, Wheelhouse, Aerodynamics, Vehicle Aerodynamics

1. Introduction
The numerical study for the calculation of aerodynamic forces arising in a vehicle has become more conventional. The methods usually employed for the analysis of such forces in vehicles are designed after the devise of prototypes in wind tunnels, which are very expensive demanding a large amount of equipment, facilities and skilled labor.
Currently companies have performed three-dimensional construction of their models, thus facilitating pro- cesses of tools construction, assembly interference checking and also allowing the numerical analysis.
Most of the articles related to numerical studies of vehicle aerodynamics aim at the vehicle body [1] or phenomena associated with lateral wind [2] generally disregarding components as the wheel geometries, tire, brake assembly (disc and caliper), suspension, shock absorber, stub axle and wheelhouse.
This article aims to determine the flow influence on a passenger vehicle using a one-fourth model of a complete vehicle as seen in Figure 1.
Many researchers have been trying to understand the complex flow patterns around vehicles, developing measurement techniques in wind tunnels [3] and computational efforts [4] . Few of the studies [5] , however, are concentrated in the region of wheelhouse. Generally, the studies include the complete vehicle and indirectly study the region of the wheelhouse.
The aim of this study is to identify, through numerical simulations, the effects of internal elements of the wheelhouse, the wheelhouse itself, the wheel and tire assembly in drag force of a passenger vehicle, through the modelling of a quarter car.
Figure 1. One-fourth model and components to be evaluated.
2. Mathematical Model and Boundary Conditions
The finite volume method was used to solve the conservation equations applied to an unstructured mesh. The equations solved for the model are respectively, the mass and the momentum conservation equations. It is used the standard k − ε model [6] for the turbulence treatment and the fluid is air at a temperature (T) of 25˚C. The flow regime is transient, varying the inlet velocity (vin) of the fluid and the soil (vg) from zero to 33.5 m/s (vin = vg). Mach number (M) for the proposed condition in this analysis is less than 0.3 so the flow can also be considered as incompressible [7] and thermal effects are neglected, i.e. isothermal flow. The wheel angular velocity (w) can be expressed as a function of ground speed and the dynamic tire radius (rd) [8] . The boundary conditions are: non-slip flow for the vehicle surfaces, free-slip flow on the top and side walls and symmetry for the zx plane as presented in Figure 2.
A simplification of some elements was adopted for the proposed model given that other geometries exert little influence on the flow. These elements are the hood of the constant velocity joint, wheel bolts case, braking set details, etc. The respective changes can be observed in Figure 3.
The approach presented by Stern and Wilson [9] [10] to define and verify the mesh is used in this paper. They discuss the mesh dependency on the results focusing the element size definition in order to validate the CFD models. The methodology considers an increase of the mesh density for the same boundary condition using predefined ratios. This procedure must be performed in such a way that property variation or small variations are not present. When this condition is satisfied the solution is considered independent of the mesh. The computational domain for the last refinement iteration process has 2.8 million elements. In Figure 4(a) it is possible to observe the surface elements applied to the vehicle body. A greater density of elements has been applied inside the wheelhouse and the tire. Figure 4(b) and Figure 4(d), and an auxiliary view is presented for the volume density elements verification, Figure 4(c).
3. Results and Discussion
The numerical study was performed in transient regime. In order to demonstrate the highest gradients of the quantities involved, air input speed was chosen to 33.5 m/s (120 km/h). The pressure variation as a function of the model surface is indicated on the color map of Figure 5(a). Sections in the computational domain were constructed and can be observed in Figure 5(c). Figure 5(b) shows a view (cut) in the xy plane and height (z) equal to rd. This section region is protected by the vehicle body which contributes to a small pressure variation against the other variations. The sections in the xz plane, Figure 5(d) and Figure 5, detail A, show respectively, the
Figure 2. Boundary conditions for the numerical model.
Figure 3. Geometrical simplifications.
Figure 4. (a) Triangular elements in the region of the vehicle body; (b) Surface elements applied on the wheel geometry; (c) Detail view in the xy plane of the wheelhouse region; (d) Superficial elements inside the wheelhouse.
Figure 5. (a) Pressure gradient applied to the vehicle surface; (b) Pressure gradient on xy plane at axis z equal to rd; (c) Illustration showing the positions of sections; and (d) Pressure gradient applied to xz plane at various positions.
pressure gradient in the section and on the surface geometry tire/wheel. Also in Figure 5 the frontal location of the vehicle shows stagnation regions, this behavior indicates consistency in the numerical results [11] .
In Figure 6 streamlines colored by velocity gradient were constructed in order to make evident the flow behavior. Figure 6 also shows that the vehicle external geometry does not originates vortex structures. This vortex structures occur only in the lower region of the wheel, tire and wheelhouse.
Vortex structures appeared depending on the geometry of the wheelhouse as shown in Figure 7. This characteristic in some cases depending on the vortex frequency emission can excite surface so as to promote noise. However, this simulation does not take into consideration such factors. Another problem associated with the formation of these vortex inside the wheelhouse is the decrease of the air flow that cools the brake system. Thus in the wheelhouse design these recirculation structures should be avoided [12] .
The aerodynamic drag force (Fa) according to Fox and McDonald [7] is defined by Equation (1):
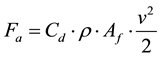 (1)
(1)
where: Cd―aerodynamic drag coefficient, ρ―density and Af―frontal area.
The aerodynamic drag coefficient is not constant [13] . It depends directly on the flow characteristics. Thus the Reynolds number is defined by Equation (2):
Figure 6. Streamlines in the proximity of the vehicle surface.
Figure 7. Cross section of the gradient and velocity vectors on the xy plane and z = 290 mm.
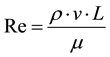 (2)
(2)
where: L is the is the characteristic length chosen as 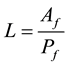 and Pf perimeter as function of the frontal area.
and Pf perimeter as function of the frontal area.
The respective areas and perimeters for this model can be observed in Figure 8.
The numerical simulations and experimental results reported in the literature indicate that the drag coefficient values vary slightly from a given speed [14] . In such cases, the value stabilizes, even with the increased speed and allows it to be defined as aerodynamic characteristics of the body. Gillespie, 1992 [8] presents average values tables for the drag coefficient as a function of the vehicle category which is proper only for estimates.
For the verification of such feature a graph of velocity versus drag coefficient was built. The vehicle body and the whole vehicle body have different drag coefficients, but show the same trend as shown in Figure 9.
Figure 10 presents the drag force projected in the x direction as a function of velocity. As expected the greatest strength comes from the vehicle body, nevertheless the geometry effect of the tire, wheel and wheelhouse are significant and together come to 16.3% of the total drag force in this direction at a speed of 33.5 (m/s) and is directly proportional to the velocity.
The internal elements of the wheelhouse exert a small influence on the total drag force of the vehicle. It is about 0.4%, so that adopted simplification compared with the order of magnitude of other elements is very much reasonable.
4. Conclusions
The main conclusions of the study are:
Figure 8. Vehicle frontal projection.
Figure 9. Inlet velocity and Reynolds number as a function of the drag coefficient.
Figure 10. Inlet speed as a function of the strength’s projection in the x direction.
1) It is possible the use of mathematical models for predicting aerodynamic loads;
2) Flow inside the wheelhouse is complex and presents recirculation regions;
3) Mechanical elements within the wheelhouse had simplified geometry and were incorporated into the model; however, the contribution to the drag force of such elements is quantitatively less than that of the wheelhouse and assembly wheel and tire;
4) According to the simulations, presented in paper, neglecting the effects of the box on wheels and wheel tire set is not suitable in aerodynamic vehicle research, except at low speeds where the aerodynamic loads are low for any vehicle.
References
- Beaudoin, J.-F. and Aider, J.-L. (2008) Drag and Lift Reduction of a 3D Bluff Body Using Flaps. Experiments in Fluids, 44, 491-501. http://dx.doi.org/10.1007/s00348-007-0392-1
- Corin, R.J., He, L. and Dominy, R.G. (2008) A CFD Investigation into the Transient Aerodynamic Forces on Overtaking Road Vehicle Models. Journal of Wind Engineering and Industrial Aerodynamics, 96, 1390-1411. http://dx.doi.org/10.1016/j.jweia.2008.03.006
- Cogotti, A. (2008) Evolution of Performance of an Automotive Wind Tunnel. Journal of Wind Engineering and Industrial Aerodynamics, 96, 667-700. http://dx.doi.org/10.1016/j.jweia.2007.06.007
- Guilmineau, E. (2008) Computational Study of Flow around a Simplified Car Body. Journal of Wind Engineering and Industrial Aerodynamics, 96, 1207-1217. http://dx.doi.org/10.1016/j.jweia.2007.06.041
- Regert, T. and Lajos, T. (2007) Description of Flow Field in the Wheelhouses of Cars. International Journal of Heat and Fluid Flow, 28, 616-629. http://dx.doi.org/10.1016/j.ijheatfluidflow.2007.04.017
- Launder, B.E. and Spalding, D.B. (1974) The Numerical Computation of Turbulent Flows. Computer Methods in Applied Mechanics and Engineering, 3, 269-289. http://dx.doi.org/10.1016/0045-7825(74)90029-2
- Fox, R.W., McDonald, A.T. and Pritchard, P.J. (1985) Introduction to Fluid Mechanics. Vol. 7, John Wiley & Sons, New York.
- Gillespie, T.D. (1992) Fundamentals of Vehicle Dynamics. Vol. 400, Society of Automotive Engineers Warrendale. http://dx.doi.org/10.4271/R-114
- Stern, F., Wilson, R.V., Coleman, H.W. and Paterson, E.G. (2001) Comprehensive Approach to Verification and Validation of CFD Simulations―Part 1: Methodology and Procedures. Journal of Fluids Engineering, 123, 793-802. http://dx.doi.org/10.1115/1.1412235
- Wilson, R.V., Stern, F., Coleman, H.W. and Paterson, E.G. (2001) Comprehensive Approach to Verification and Validation of CFD Simulations―Part 2: Application for Rans Simulation of a Cargo/Container Ship. Journal of Fluids Engineering, 123, 803-810. http://dx.doi.org/10.1115/1.1412236
- Duell, E.G. and George, A.R. (1999) Experimental Study of a Ground Vehicle Body Unsteady near Wake. Technical report, SAE Technical Paper.
- Landström, C., Löfdahl, L. and Walker, T. (2009) Detailed Flow Studies in Close Proximity of Rotating Wheels on a Passenger Car. Technical Report, SAE Technical Paper.
- Cengel, Y.A. and Cimbala, J.M. (2006) Fluid Mechanics. Vol. 1, Tata McGraw-Hill Education, New York.
- White, F.M. and Corfield, I. (2006) Viscous Fluid Flow. Vol. 3, McGraw-Hill, New York.











