Journal of Applied Mathematics and Physics
Vol.03 No.06(2015), Article ID:57631,10 pages
10.4236/jamp.2015.36085
Analysis of Casson Fluid Flow over a Vertical Porous Surface with Chemical Reaction in the Presence of Magnetic Field
Emmanuel Maurice Arthur1, Ibrahim Yakubu Seini1, Letis Bortey Bortteir2
1Department of Mathematics, University for Development Studies, Navrongo, Ghana
2Department of Physics, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana
Email: jimknights01@yahoo.com, yakubuseini@yahoo.com, letiso2000@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 November 2014; accepted 27 June 2015; published 30 June 2015
ABSTRACT
Casson fluid flow over a vertical porous surface with chemical reaction in the presence of magnetic field has been studied. A similarity analysis was used to transform the system of partial differential equations describing the problem into ordinary differential equations. The reduced system was solved using the Newton Raphson shooting method alongside the Forth-order Runge-Kutta algorithm. The results are presented graphically and in tabular form for various controlling parameters.
Keywords:
Magnetic Field, Casson Fluid, Mass Transfer, Suction, Non-Newtonian Fluid

1. Introduction
A fluid in which the viscous stresses arising from its flow at every point are linearly proportional to the rate of change in its deformation over time is called Newtonian fluid. This means that in a Newtonian fluid, the relationship between the shear stress and the shear rate is linear with the proportionality constant to refer to as the coefficient of viscosity. On the other hand, a fluid whose flow properties are different in any way from that of the Newtonian fluid is called a non-Newtonian fluid. Unlike the Newtonian fluids, the viscosity of non-Newto- nian fluid is dependent on shear rate history. That is to say, in a non-Newtonian fluid, the relationship between the shear stress and the shear rate is different and can even be time dependent. Thus a constant coefficient of viscosity cannot be defined. Some examples of non-Newtonian fluids are salt solutions, molten polymers, ketchup, custard, toothpaste, starch suspensions, paints, blood and shampoo.
It is important to note here that, many fluids of industrial importance are non-Newtonian. It is now generally recognized that, in real industrial applications, non-Newtonian fluids are more appropriate than Newtonian fluids, due to their applications in petroleum drilling, polymer engineering, certain separation processes, manufacturing of foods and paper and some other industrial processes [1] [2] . Due to the nonlinearity between the stress and the rate of strain for non-Newtonian fluids, it is difficult to express all those properties of several non- Newtonian fluids in a single constitutive equation. This has called on the attention of researchers to the analysis of flow dynamics of non-Newtonian fluids. Consequently, several non-Newtonian fluid models [3] - [10] have been proposed depending on various physical characters. The most popular among these fluids is the Casson fluid.
Casson fluid can be defined as a shear thinning liquid which is assumed to have an infinite viscosity at zero rate of shear, a yield stress below which no flow occurs and a zero viscosity at an infinite rate of shear [11] . The nonlinear Casson’s constitutive equation has been found to describe accurately the flow curves of suspensions of pigments in the lithographic vanishes used for the preparation of printing inks [12] and silicon suspensions [13] . The shear stress-shear rate relation given by Casson satisfactorily describes the properties of many polymers over a wide range of shear rates [14] . Various experiments performed on blood with varying haematocrits, anticoagulants, temperatures, and the likes, strongly suggest the behaviour of blood as a Casson fluid [15] [16] . In particular, the Casson fluid model describes the flow characteristics of blood more accurately at low shear rates and when it flows through small blood vessels. Casson fluids are found to be applicable in developing models for blood oxygenator and haemodialysers.
Fredrickson [17] investigated the steady flow of a Casson fluid in a tube. Mustafa et al. [1] studied the unsteady boundary layer flow and heat transfer of a Casson fluid over a moving flat plate with a parallel free stream using the Homotopy Analysis Method (HAM). On the other hand, boundary layer flows of non-Newto- nian fluids caused by a stretching sheet have vast applications in several manufacturing processes such as extrusion of molten polymers through a slit die for the production of plastic sheets, hot rolling, wire and fibre coating, processing of food stuffs, metal spinning, glass-fibre production and paper production [18] . During the processes, the rate of cooling has an important bearing on the properties of the final product. Hence, the quality of the final product depends on the rate of heat transfer from the stretching surface [19] [20] .
The viscous fluid flow due to a stretching flat sheet was first investigated by Crane [21] , and this pioneering work was extended by Rajagopal et al. [22] who considered viscoelastic fluid. Siddappa and Abel [23] discussed some other important aspects of flow of non-Newtonian fluid over stretching sheets. Sankara and Watson [24] studied micropolar fluid flow over a stretching sheet. Troy et al. [25] established the uniqueness of solution of the flow of second order fluid over a stretching sheet. Andersson and Dandapat [26] reported the flow behaviour of a non-Newtonian power-law fluid over a stretching sheet. Recently Hayat et al. [27] analyzed the mixed convection stagnation-point flow of a non-Newtonian Casson fluid. Most importantly, Bhattacharyya et al. [28] recently investigated the boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet with magnetic field effect.
From literature, it can be found that not much attention is given to the Casson fluid flow over a porous vertical surface with chemical reaction in the presence of magnetic field. The increasing use of several non-Newtonian fluids in processing industries has motivated a study to understand their behaviour in several transport processes. Therefore, in this investigation, the steady incompressible Casson fluid flow and mass transfer towards a porous vertical stretching sheet are studied. The governing partial differential equations are converted into systems of nonlinear ordinary differential equations (ODE) using the suitable similarity transformations. The transformed self-similar ODEs are solved by shooting method: an efficient numerical method for solving boundary value problem [29] - [31] . Then a graphical analysis is presented to show the existence and uniqueness of solution and to elaborately discuss the characters of the flow and mass transfer for the varying parameters.
2. Mathematical Model
Consider a two-dimensional steady incompressible Casson fluid flow over a vertical porous stretching surface at y = 0 in the presence of a transverse magnetic field, as shown in Figure 1. Let the x-axis be taken along the direction of the plate and y-axis normal to it. The fluid occupies the half space y > 0. The mass transfer phenomenon with chemical reaction is also retained. The flow is subjected to a constant applied magnetic field B0 in the y direction. The magnetic Reynolds number is considered to be very small so that the induced magnetic field is
Figure 1. Schematic diagram of the problem.
negligible in comparison to the applied magnetic field. The tangential velocity uw, due to the stretching surface is assumed to vary proportionally to the distance x so that uw = ax, where a is a constant.
The rheological equation of state for an isotropic flow of a Casson fluid [32] can be expressed as:
 (1)
(1)
In Equation (1), π = eijeij; where eij is the (i, j)th component of the deformation rate. This means that π is the product of the component of deformation rate with itself. Also, πc is a critical value of this product based on the non-Newtonian model, μB is the plastic dynamic viscosity of the non-Newtonian fluid and Py is the yield stress of the fluid. If u and v are the fluid x- and y-components of velocity respectively; and C being the concentration field; then the equations governing the steady boundary layer flow of the Casson fluid are:
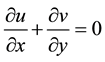 (2)
(2)
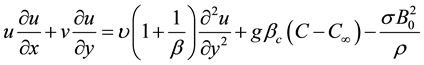 (3)
(3)
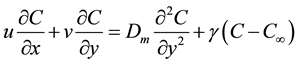 (4)
(4)
Subject to the following boundary conditions:
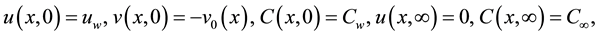 (5)
(5)
where  is the non-Newtonian Casson parameter,
is the non-Newtonian Casson parameter, 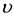 is the kinematic viscosity, Dm is the mass
is the kinematic viscosity, Dm is the mass
diffusion, γ is the reaction rate, v0(x) is the suction velocity from the surface, Cw is the concentration at the surface, C∞ is the free stream concentration, βc is the solutal expansion coefficient, ρ is the fluid density, g is gravitational acceleration, and σ is the electrical conductivity.
The following dimensionless quantities are introduced:
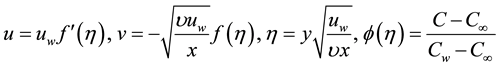 (6)
(6)
Substituting Equation (5) in (2)-(4) yields:
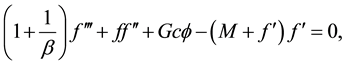 (7)
(7)
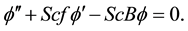 (8)
(8)
The transformed boundary conditions are
 (9)
(9)
The prime symbol denotes differentiation with respect to the similarity variable η, where  is the magnetic field parameter,
is the magnetic field parameter, 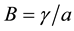 is the chemical reaction parameter,
is the chemical reaction parameter,  is the suction
is the suction
parameter, 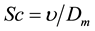 is the Schmidt number, and
is the Schmidt number, and 
3. Numerical Solution
The numerical technique chosen for the solution of the coupled ordinary differential Equations (7)-(8) together with the associated transformed boundary conditions (9) is the standard Newton-Raphson shooting method alongside the fourth-order Runge-Kutta integration algorithm. From the process of numerical computation, the plate surface temperature, the local skin-friction coefficient, the local Nusselt number and the local Sherwood number, which are respectively proportional to −f″(0) and −ϕ′(0) are computed and their numerical values presented in a tabular form.
Table 1 shows the comparison of the works of [33] -[35] with the present study for varying values of the reaction rate parameter (B) and it is clear from the table that the present study is consistent with their works. The results of varying parameter values on the local skin friction coefficient and the local Sherwood number are shown in Table 2. It is observed that the skin friction increases with increasing values of M, β, Sc, B, and fw and decreases with increasing values of GC. This means that the combined effect of magnetic field, Casson parameter, Schmidt number, reaction rate parameter and suction parameter is to increase the local skin friction; whereas that of the buoyancy force is to decrease the local skin friction at the surface of the plate. Moreover, it is observed that the rate of mass transfer increases with increasing values of fw, Gc, Sc and B; and decreases with increasing values of M and β.
4. Graphical Solution
4.1. Effects of Parameter Variation on Velocity Profiles
Figures 2-5 show the effects of the magnetic parameter (M), suction parameter (fw), Casson parameter (β), and local solutal Grashof number (Gc), respectively, on the velocity profile, f′(η). Generally, the fluid velocity is minimal at the plate surface and increases to the free stream value satisfying the far field boundary conditions.The effects of magnetic parameter (M) and the suction parameter (fw) on velocity profiles are seen in Figure 2 and Figure 3 respectively. It is observed that the combined effect of M and fw is to decrease the velocity of the flow. This is due to the fact that the transverse magnetic field induces a Lorentz force which tends to provide resistance to the fluid flow. Suction also causes resistance to the fluid flow thus a decrease in the velocity profile as shown in Figure 3.
Table 1. Comparison of values of −ϕʹ(0) for different values of B with M = fw = Gc = 0 as β → ∞.
Figure 2. Velocity profiles for varying values of magnetic field parameter.
Figure 3. Velocity profiles for varying values of suction parameter.
Figure 4. Velocity profiles for varying values of Casson parameter.
Figure 5. Velocity profiles for varying values of solutal Grash of number.
Table 2. Numerical results of skin friction coefficient and the Sherwood number.
It is observed in Figure 4 that the velocity decreases when β increases. In practice, increasing β results in an increase in the plastic dynamic viscosity that produces a resistance in the flow and a decrease in fluid velocity thereof. In addition, increasing the local Grashof number (Gc) increases the velocity of the flow as shown in Figure 5. This can be attributed to the fact that, increasing Gc causes the fluid velocity to increase due to buoyancy effect. We can note here that, increasing buoyancy force will lead to a better flow kinematics.
4.2. Effects of Parameter Variation on Concentration Profiles
Figures 6-11 show the plots of the effects of the magnetic parameter (M), suction parameter (fw), Casson parameter (β), Schmidt number (Sc) and chemical reaction parameter (B) on the concentration profile, ϕ (η) respect-tively. It is observed in Figure 6 that, by increasing M, the concentration boundary layer thickness increases. This can be attributed to the retarding force of the transverse magnetic field which retards the fluid flow
Figure 6. Concentration profiles for varying values of magnetic field parameter.
Figure 7. Concentration profiles for varying values of the suction parameter.
Figure 8. Concentration profiles for varying values of Casson parameter.
Figure 9. Concentration profiles for varying values of Schmidt number.
Figure 10. Concentration profiles for varying values of reaction rate parameter.
Figure 11. Concentration profiles for varying values of local solutal Grashof number.
to increase concentration thereof. The concentration profile decreases with increasing fw as shown in Figure 7. This is due to the fact that suction gives the fluid flow some resistance upon increasing the friction between its layers and hence, a decrease in concentration. In Figure 8, the concentration boundary layer thickness increases with increasing values of β. This is as a result of the retarding force induced by the plastic viscosity thus increasing concentration. It is noteworthy from Figure 4 and Figure 8 that the Casson parameter β has quite opposite effect on the velocity and concentration profiles. Figure 9 depicts that the concentration boundary layer thickness decreases with increasing values of Sc. In practice, increasing Schmidt number means increasing momentum diffusion over mass diffusion which in turn reduces the concentration profile.
At a point in the flow where B is zero implies no chemical reaction. On the other hand, an increase in B means an increase in the chemical reaction rate which causes a reduction in concentration. Figure 10 affirms this where increasing values of B decreases the concentration boundary layer. Moreover, it is observed in Figure 11 that increasing the buoyancy force due to chemical species concentration has adverse effect of decaying the concentration boundary layer thickness.
5. Conclusions
An analysis of Casson fluid flow over a vertical porous surface with chemical reaction in the presence of a transverse magnetic field has been presented. Numerical results have been compared to earlier results published in the literature and a perfect agreement was achieved. Among others, our results reveal that:
1) The velocity decreases with the increase in values of M, fw and β; and increases with increasing values of Gc.
2) The concentration boundary layer decreases with increasing values of fw, Gc, Sc and B; and increases with increasing values of M and β.
3) The skin friction at the surface increases with increasing values of M, fw, β, Sc and B; and decreases for increasing values of Gc.
4) The rate of mass transfer at the surface increases with increasing values of fw, Gc, Sc and B; and decreases with increasing values of M and β.
References
- Mustafa, M., Hayat, T., Pop, I. and Aziz, A. (2011) Unsteady Boundary Layer Flow of a Casson Fluid Due to an Impulsively Started Moving Flat Plate. Heat Transfer-Asian Research, 40, 563-576. http://dx.doi.org/10.1002/htj.20358
- Cortell, R. (2008) Analysing Flow and Heat Transfer of a Viscoelastic Fluid over a Semi-Infinite Horizontal Moving Flat Plate. International Journal of Non-Linear Mechanics, 43, 772-778. http://dx.doi.org/10.1016/J.Ijnonlinmec.2008.04.006
- Fox, V.G., Erickson, L.E. and Fan, L.T. (1969) The Laminar Boundary Layer on a Moving Continuous Flat Sheet Immersed in a Non-Newtonian Fluid. AIChE Journal, 15, 327-333. http://dx.doi.org/10.1002/aic.690150307
- Wilkinson, W. (1970) The Drainage of a Maxwell Liquid Down a Vertical Plate. Chemical Engineering Journal, 1, 255-257. http://dx.doi.org/10.1016/0300-9467(70)80008-9
- Djukic, D.S. (1974) Hiemenz Magnetic Flow of Power-Law Fluids. Journal of Applied Mechanics, 41, 822-823. http://dx.doi.org/10.1115/1.3423405
- Rajagopal, K.R. (1980) Viscometric Flows of Third Grade Fluids. Mechanics Research Communications, 7, 21-25. http://dx.doi.org/10.1016/0093-6413(80)90020-8
- Rajagopal, K.R. and Gupta A.S. (1981) On a Class of Exact Solutions to the Equations of Motion of a Second Grade Fluid. International Journal of Engineering Science, 19, 1009-1014. http://dx.doi.org/10.1016/0020-7225(81)90135-X
- Dorier, C. and Tichy, J. (1992) Behaviour of a Bingham-Like Viscous Fluid in Lubrication Flows. Journal of Non- Newtonian Fluid Mechanics, 45, 291-310. http://dx.doi.org/10.1016/0377-0257(92)80065-6
- Zhou, X.-F. and Gao, L. (2007) Effect of Multipolar interaction on the Effective Thermal Conductivity of Nanofluids. Chinese Physics B, 16, 2028-2032. http://dx.doi.org/10.1088/1009-1963/16/7/037
- Cui, Z.W., Liu, J.X., Yao, G.J. and Wang, K.X. (2010) Borehole Guided Waves in a Non-Newtonian (Maxwell) Fluid-Saturated Porous Medium. Chinese Physics B, 19, 084301. http://dx.doi.org/10.1088/1674-1056/19/8/084301
- Dash, R.K., Mehta, K.N. and Jayaraman, G. (1996) Casson Fluid Flow in a Pipe Filled with a Homogeneous Porous Medium. International Journal of Engineering Science, 34, 1145-1156.
- Casson, N. (1959) A Flow Equation for Pigment-Oil Suspensions of the Printing Ink Type. In: Mill, C.C., Ed., Rheology of Disperse Systems, Pergamon Press, Oxford, 84-104.
- Walwander, W.P., Chen, T.Y. and Cala, D.F. (1975) An Approximate Casson Fluid Model for Tube Flow of Blood. Biorheology, 12, 111-119.
- Vinogradov, G.V. and Malkin, A.Y. (1979) Rheology of Polymers. Mir Publisher, Moscow.
- Blair, G.W.S. (1959) An Equation for the Flow of Blood, Plasma and Serum through Glass Capillaries. Nature, 183, 613-614. http://dx.doi.org/10.1038/183613a0
- Charm, S. and Kurland, G. (1965) Viscometry of Human Blood for Shear Rates of 0-100,000 sec−1. Nature, 206, 617- 618. http://dx.doi.org/10.1038/206617a0
- Fredrickson, A.G. (1964) Principles and Applications of Rheology. Prentice-Hall, Englewood Cliffs.
- Hayat, T., Sajid, M. and Pop, I. (2008) Three-Dimensional Flow over a Stretching Surface in a Viscoelastic Fluid. Nonlinear Analysis: Real World Applications, 9, 1811-1822. http://dx.doi.org/10.1016/j.nonrwa.2007.05.010
- Bhattacharyya, K. (2013) Boundary Layer Stagnation-Point Flow of Casson Fluid and Heat Transfer towards a Shrinking/Stretching Sheet. Frontiers in Heat and Mass Transfer (FHMT), 4, Article ID: 023003. http://dx.doi.org/10.5098/hmt.v4.2.3003
- Arthur, E.M. and Seini, Y.I. (2014) MHD Thermal Stagnation Point Flow towards a Stretching Porous Surface. Mathematical Theory and Modeling, 4, 163-169.
- Crane, L.J. (1970) Flow past a Stretching Plate. Zeitschrift für angewandte Mathematik und Physik, 21, 645-647. http://dx.doi.org/10.1007/BF01587695
- Rajagopal, K.R., Na, T.Y. and Gupta, A.S. (1984) Flow of Viscoelastic Fluid over a Stretching Sheet. Rheologica Acta, 23, 213-215. http://dx.doi.org/10.1007/BF01332078
- Siddappa, B. and Abel, M.S. (1985) Non-Newtonian Flow past a Stretching Plate. Zeitschrift für angewandte Mathematik und Physik, 36, 890-892. http://dx.doi.org/10.1007/BF00944900
- Sankara, K.K. and Watson, L.T. (1985) Micropolar Flow Past a Stretching Sheet. Zeitschrift für angewandte Mathematik und Physik, 36, 845-853. http://dx.doi.org/10.1007/BF00944898
- Troy, W.C., Overman, E.A., Ermentrout, H.G.B. and Keerner, J.P. (1987) Uniqueness of the Flow of a Second Order Fluid past a Stretching Sheet. The Quarterly of Applied Mathematics, 44, 753-755.
- Andersson, H.I. and Dandapat, B.S. (1991) Flow of a Power-Law Fluid over a Stretching Sheet. Stability Applied Analysis of Continuous Media, 1, 339-347.
- Hayat, T., Shehzad, S.A., Alsaedi, A. and Alhothuali, M.S. (2012) Mixed Convection Stagnation Point Flow of Casson Fluid with Convective Boundary Conditions. Chinese Physics Letters, 29, Article ID: 114704. http://dx.doi.org/10.1088/0256-307X/29/11/114704
- Bhattacharyya, K., Hayat, T. and Alsaedi, A. (2013) Analytic Solution for Magnetohydrodynamic Boundary Layer Flow of Casson Fluid over a Stretching/Shrinking Sheet with Wall Mass Transfer. Chinese Physics B, 22, Article ID: 024702. http://dx.doi.org/10.1088/1674-1056/22/2/024702
- Mahapatra, T.R. and Nandy, S.K. (2013) Stability of Dual Solutions in Stagnation-Point Flow and Heat Transfer over a Porous Shrinking Sheet with Thermal Radiation. Meccanica, 48, 23-32. http://dx.doi.org/10.1007/s11012-012-9579-5
- Ishak, A., Lok, Y.Y. and Pop, I. (2010) Stagnation-Point Flow over a Shrinking Sheet in a Micropolar Fluid. Chemical Engineering Communications, 197, 1417-1427. http://dx.doi.org/10.1080/00986441003626169
- Yacob, N.A., Ishak, A. and Pop, I. (2011) Melting Heat Transfer in Boundary Layer Stagnation-Point Flow towards a Stretching/Shrinking Sheet in a Micropolar Fluid. Computers & Fluids, 47, 16-21. http://dx.doi.org/10.1016/j.compfluid.2011.01.040
- Eldabe, N.T.M. and Salwa, M.G.E. (1995) Heat Transfer of MHD Non-Newtonian Casson Fluid Flow between Two Rotating Cylinders. Journal of the Physical Society of Japan, 64, 41.
- Andersson, H.I., Hansen, O.R. and Holmedal, B. (1994) Diffusion of a Chemically Reactive Species from a Stretching Sheet. International Journal of Heat and Mass Transfer, 37, 659-664. http://dx.doi.org/10.1016/0017-9310(94)90137-6
- Salem, A.M. and El-Aziz, M.A. (2008) Effect of Hall Currents and Chemical Reaction on Hydromagnetic Flow of a Stretching Vertical Surface with Internal Heat Generation/Absorption. Applied Mathematical Modelling, 32, 1236- 1254. http://dx.doi.org/10.1016/j.apm.2007.03.008
- Shehzad, S.A., Hayat, T., Qasim, M. and Asghar, S. (2013) Effects of Mass Transfer on MHD Flow of Casson Fluid with Chemical Reaction and Suction. Brazilian Journal of Chemical Engineering, 30, 187-195. http://dx.doi.org/10.1590/S0104-66322013000100020













