Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2009, 2: 335-343 doi:10.4236/jsea.2009.25044 Published Online December 2009 (http://www.SciRP.org/journal/jsea) Copyright © 2009 SciRes JSEA 335 An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Xiuhong WANG Zhengzhou Institute of Aeronautical Management, Zhengzhou, China. Email: wangzzia@zzia.edu.cn Received July 31st, 2009; revised September 14th, 2009; accepted September 21st, 2009. ABSTRACT Integrated use of statistical process control (SPC) and engineering process control (EPC) has better performance than that by solely using SPC or EPC. But integrated scheme has resulted in the problem of “Window of Opportunity” and autocorrelation. In this paper, advanced T2 statistics model and neural networks scheme are combined to solve the above problems: use T2 statistics technique to solve the problem of autocorrelation; adopt neural networks technique to solve the problem of “Window of Opportunity” and identification of disturbance causes. At the same time, regarding the shortcoming of neural network technique that its algorithm has a low speed of convergence and it is usually plunged into local optimum easily. Genetic algorithm was proposed to train samples in this paper. Results of the simulation ex- periments show that this method can detect the process disturbance quickly and accurately as well as identify the dis- turbance type. Keywords: T2 Statistics, Neural Networks, Statistical Process Control, Engineering Process Control, Genetic Algorithm 1. Introduction In an intense market competition environment, product quality plays an important role in facing competition and gaining competitiveness. Both Statistical Process Control (SPC) and Engineering Process Control (EPC) are effec- tive techniques of maintaining and improving the pro- duce quality. EPC is used to adjust the variables for compensating the short-term output deviation by uncon- trollable factors. In regard to long-term process im- provement, SPC is effective technique which is used to detect out-of-control conditions and remove the control- lable factors. So, lots of scholars have proposed the inte- grated use of SPC/EPC. However, it is very difficult to monitor the EPC proc- ess using commonly SPC methods because of the prob- lem of “Window of Opportunity” and autocorrelation [1]. In the past time, monitored variable of SPC techniques was only process output. The information of process in- puts was usually ignored. For the EPC processes, once output deviation is compensated by feedback-controlled action, there is only a short window of detecting process disturbance. Even SPC charts fail to detect out-of-control when output deviation is small because EPC’s feedback mechanism can compensate for such small disturbance quickly and completely. And the optimality of SPC tech- niques rests on the assumption of time independence. However, process output of no same time is autocorrela- tion for each other. To overcome these shortcomings, a little of papers have developed some joint-monitoring methods under the feedback control processes. These methods may be categorized into two aspects. The first is that various types of conventional SPC charts are integrated to moni- tor the process [2–3], such as Huang C.H proposed She- whart control chart and Cusom control chart simultane- ously to detect the manufacturing process. This method can detect out-of-control, also can recognize the distur- bance type. However, the inherent problems of conven- tional SPC charts caused by the effects of feedback con- trol actions have still not been solved. The second is that the strategy of jointly detecting the controlled outputs and manipulated inputs using bipartite SPC is suggested such as multivariate CUSUM chart, multivariate EWMA chart, T 2 statistics and multivariate profile chart [4,5]. Although, these methods have solved effectively the autocorrelation problem, but the WO problem has not been settled completely and effectively because these methods can not monitor the small process disturbance quickly within the scope of the WO. Furthermore, these  An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 336 methods are not easy to identify the disturbance types which are crucial links of confirm and remove the con- trollable factors. In this research, we put forward a new program of in- tegrated use of T 2 statistics technique, artificial neural networks and genetic algorithm: use T 2 statistics tech- nique to solve the problem of autocorrelation and infor- mation missing; adopt neural networks technique and genetic algorithm to solve the problem of “Window of Opportunity” and identification of disturbance causes. 2. Feedback-Controlled Process For better understanding, we consider the following process under the feedback mechanism shown in Figure 1. We consider an integrated-moving-average noise mo- del (ARMA (1, 1)). 1 1 tt B da B θ φ − =− (1) Where θ, Φ are constants. аt represents white noise which complies with a standard normal distribution with mean =0 and σ2=1. Also, let B be the usual backward shift op- erator, i.e., Bа t =а t-1. mt represents random form of the process disturbance such as step change and process drift. yt is the measured output value. Without loss of gener- ality, the target value is assumed to be zero. Then, y t represents the output deviation from the target value. 1 ttttttt ydmxdmu − =++=++ (2) ut is the feedback control action decided by the feed- back process mechanism. In the industrial practice, sev- eral feedback controllers are used such as PI controllers, I controllers, PID controller and EWMA controllers in which PID controllers are the most extensively adopted. Its feedback control rules can be expressed as [6]. 1 0 () tPtItjDtt j ukykykyy ∞ −− = =−−−− ∑ (3) where k p ,kD ,kI are constants. Function 3 can also be expressed as 112 ()(2) ttPIDtPDtDt uukkkykkyky −−− −=−+++++ (4) Process Feedback Mechanism y t d t x t u t y t m t Figure 1. Feedback-controlled process In light of the function 4, output at the different times is autocorrelation, and input at the different times is auto- correlation. Moreover, output and input are autocorrela- tion for each other. So, traditional SPC control charts, such as Shewhart chart, EWMA chart and Cusum chart are invalid to monitor the above process. 3. Design of the New Methodology 3.1 Design of Standard T2 Statistics Technique Standard T 2 statistics method is used to deal with the multiple-input process. In this paper, the devised ap- proach is similar to the standard T2 statistics but the data vectors are made up of the process input and output at the different times. It can measure the overall distance of observation from reference values including process output, input and covariance of output and input, hence, it will come to the most commonly used schemes. Ac- cording to the function 4, complete monitoring informa- tion should include control action at time t and t-1, the process output at time t, t-1 and t-2. However, to detect the closed-loop process, the five sets are co-linear. In other words, arbitrary set is equal to a linear combination of other sets. So, we can only select two sets, three sets or four sets from the above five sets to make the moni- toring scheme. We design the monitoring model of T 2 statistics as follows 1T ttt DZZ − = ∑ (5) Where Σ is the covariance matrix of Zt . In light of the above analysis, the options N of Zt are equal to 432 555 NCCC =++ (6) There is not commonly admitted approach for con- firming the best Z t selection in the T2 statistics model. Selection of the model parameter is based on the problem which will be solved. Therefore, the design of model is scientific as well as art. Hotelling, Montgomery and Alt discussed the possibilities and advantages of the T2 sta- tistics method used to monitor the EPC process [7–9]. They designed the simplest and the most basic form of Zt, i.e. Zt = [yt,ut]. On the basis of the above study, FUGEE TSUNG elaborated on the problem and proposed that one could define Z t =[yt,ut,ut-1,ut-2]T or Z t =[yt, u t , y t-1, yt-2]T [1]. However, in these methods, ∑ is not estimated from the historical data directly, but obtained from a very complex function based on the parameter of Φ, θ, kp ,kD ,kI. So the T2 control chart is not available for these methods. According to function 2 and 3, since outputs and in- puts are correlated, all inputs can be expressed as the combination of the process outputs at different times. In other words, all information concluding the process in- puts and the process outputs can be monitored as long as we detect the outputs at different times. 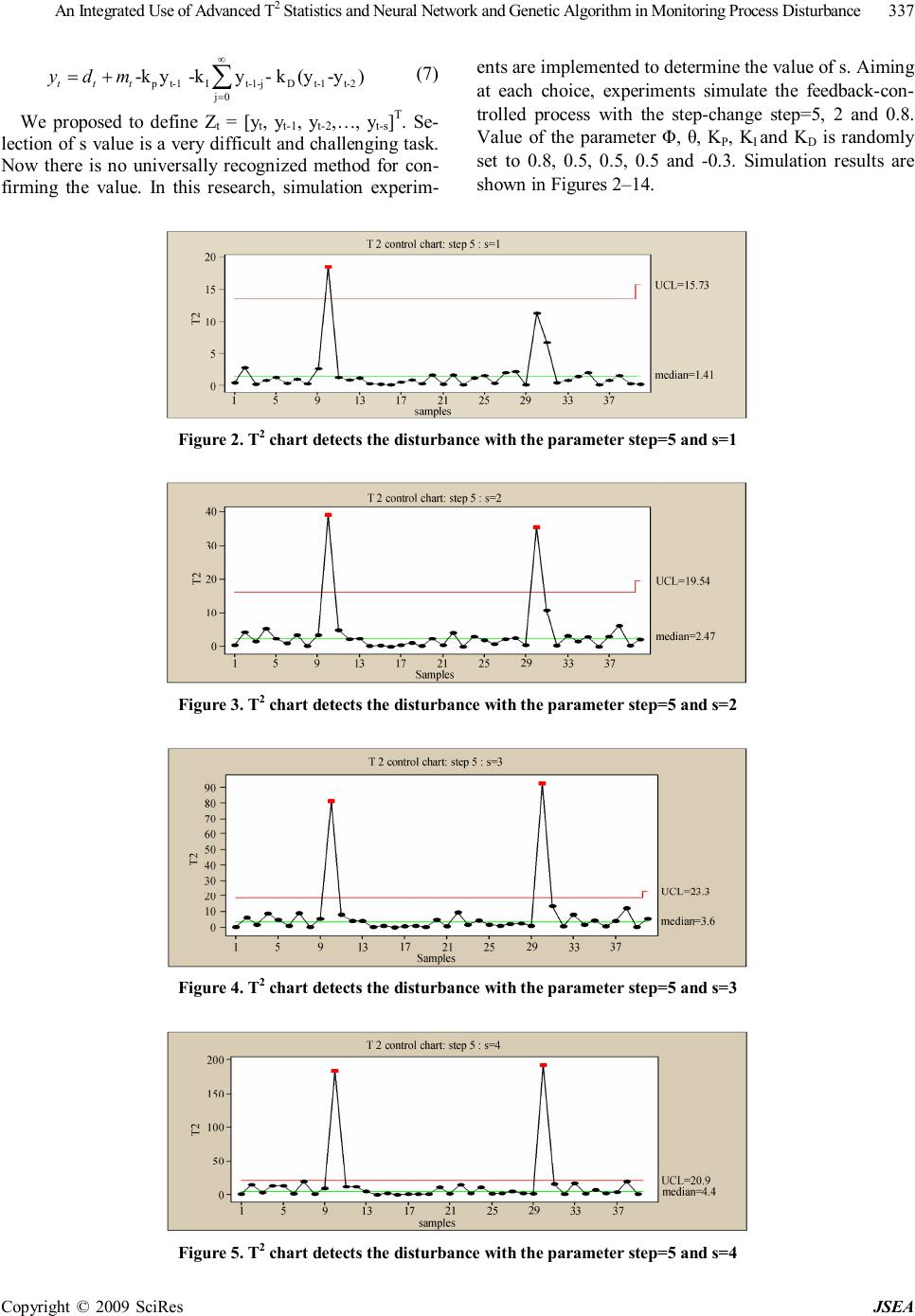 An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 337 pt-1It-1-jDt-1t-2 j0 -ky -ky- k(y-y) ttt ydm ∞ = =+ ∑ (7) We proposed to define Zt = [yt, yt-1, yt-2,…, yt-s]T. Se- lection of s value is a very difficult and challenging task. Now there is no universally recognized method for con- firming the value. In this research, simulation experim- ents are implemented to determine the value of s. Aiming at each choice, experiments simulate the feedback-con- trolled process with the step-change step=5, 2 and 0.8. Value of the parameter Φ, θ, KP, KI and KD is randomly set to 0.8, 0.5, 0.5, 0.5 and -0.3. Simulation results are shown in Figures 2–14. Figure 2. T2 chart detects the disturbance with the parameter step=5 and s=1 Figure 3. T2 chart detects the disturbance with the parameter step=5 and s=2 Figure 4. T2 chart detects the disturbance with the parameter step=5 and s=3 Figure 5. T2 chart detects the disturbance with the parameter step=5 and s=4 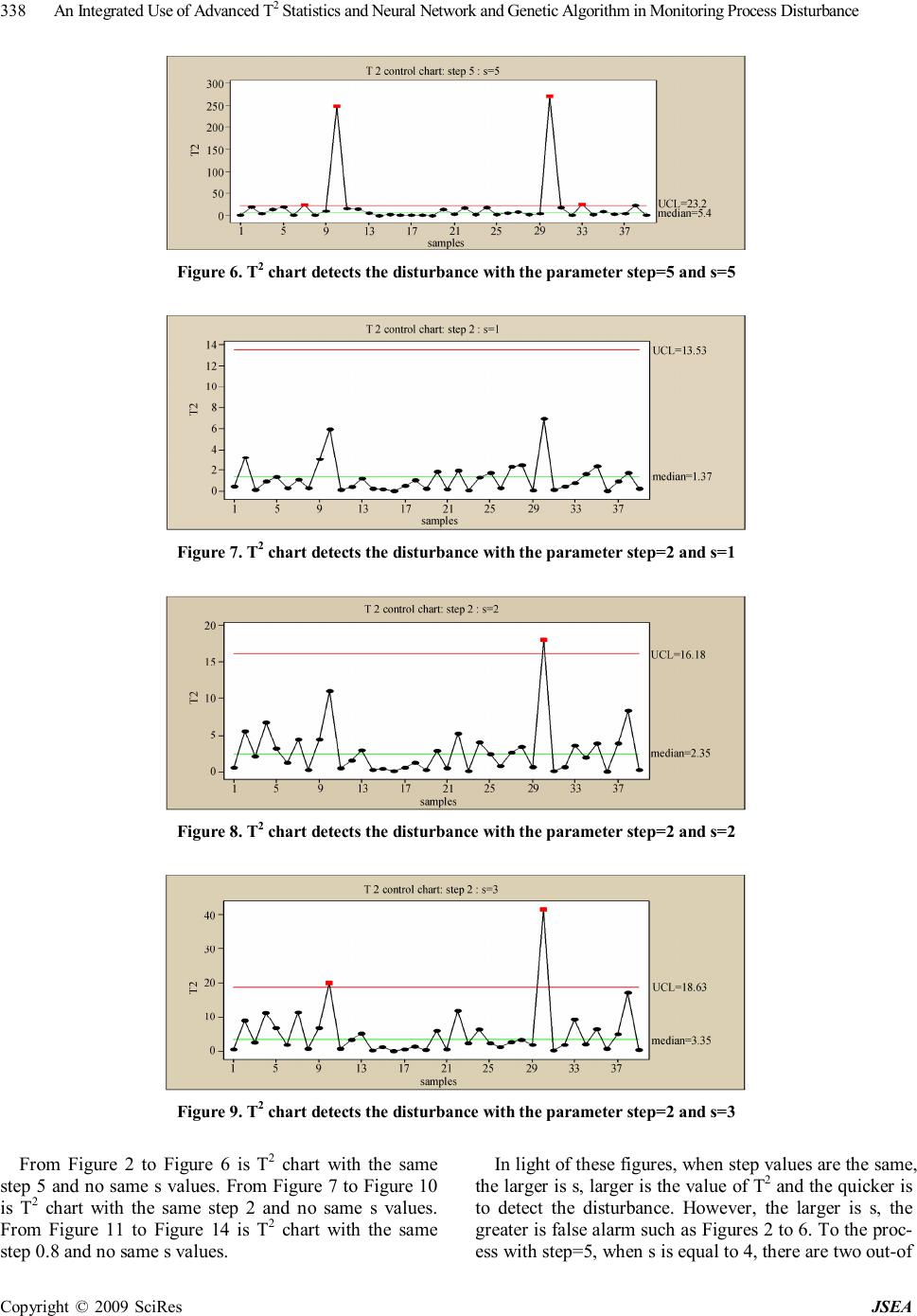 An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 338 Figure 6. T2 chart detects the disturbance with the parameter step=5 and s=5 Figure 7. T2 chart detects the disturbance with the parameter step=2 and s=1 Figure 8. T2 chart detects the disturbance with the parameter step=2 and s=2 Figure 9. T2 chart detects the disturbance with the parameter step=2 and s=3 From Figure 2 to Figure 6 is T2 chart with the same step 5 and no same s values. From Figure 7 to Figure 10 is T2 chart with the same step 2 and no same s values. From Figure 11 to Figure 14 is T2 chart with the same step 0.8 and no same s values. In light of these figures, when step values are the same, the larger is s, larger is the value of T2 and the quicker is to detect the disturbance. However, the larger is s, the greater is false alarm such as Figures 2 to 6. To the proc- ess with step=5, when s is equal to 4, there are two out-of  An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 339 Figure 10. T2 chart detects the disturbance with the parameter step=2 and s=4 Figure 11. T2 chart detects the disturbance with the parameter step=0.8 and s=1 Figure 12. T2 chart detects the disturbance with the parameter step=0.8 and s=2 Figure 13. T2 chart detects the disturbance with the parameter step=0.8 and s=3 control points. However, when s is equal to 5, there are four out-of control points in which two points fall into false alarm. In the same way, to the process with step 2 and step 0.8, when s increases from s=2 to s=4, the dots of false alarm grow from 0 to 2. To the different step changes, the smaller is step value, the larger is to need the value of s to detect the process. For example, it only need s=1 to monitor the process with step=5, but need s=3 to detect the process with step=2 and step =0.8.  An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 340 Figure 14. T2 chart detects the disturbance with the parameter step=0.8 and s=4 Figure 15. Feedback-controlled process According to Figure 2–14 and the above analysis, Z t can be expressed as Zt = [yt, yt-1, yt-2, yt-3]T. In light of the function 7, yt is a linear combination of the yt-i, (i=0, 1, 2, 3). So Zt accords with a multivariate normal distribution and Zt has a chi-squared distribution with p degrees-of- freedom. The control limit UCL for Zt should be χ2α,p. Dt contains the information of output, input and corre- lation for each other. So the advanced T2 statistics can solve effectively the problem of autocorrelation and re- duce the problem of “Window of Opportunity”. More- over, it is difficult to interpret the results and search for the root cause of process disturbance once system moni- tored out-of-control such as Figure 15. Figure 15 shows the process with the drift disturbance slope=1. But it has not essential distinction between Fig- ure 15 and Figure 2–14 to identify the disturbance type such as significant upward or downward trend. So, ad- vanced T2 statistics technique can not be used solely. 3.2 Artificial Neural Networks Artificial neural networks are modeled following the neural activity in human brain and rapidly developed since the last century 80’s [10]. The main characteristics of neural networks are the overall use of network, Large- scale parallel distributed processing, Ability to study association, high degree of fault tolerance and robustness. However, neural networks are easy to fall into local op- timum, slow convergence and cause oscillation effect. Genetic algorithm [11] has strong macro-search capabili- ties and greater probability of finding the global optimal solution. So, genetic algorithm can overcome the short- comings of neural networks if it is used to finish the pre-search. In this paper, a novel algorithm combining neural networks algorithm and genetic algorithm was proposed. The framework of neural network is shown in Figure 16. Network is composed of an input layer, a hidden layer and an output layer. Input layer has three neurons which are expressed as D t , D t-1 and D t-2 representing the pa- rameter value of T2 statistics at time t, t-1 and t-2 based on the function 4. Output layer has two neurons which are expressed as O1 and O2, where O1 represents distur- bance classification values and O2 represents disturbance causes. Hidden layer has s neurons which is expressed as HR∈ S (H=(H1, H2,…, Hs) T. WIH represents the relation weight between input layer and hidden layer. W OH Input layer H 1 O 2 W IH W OH H s O 1 D t Hidden layer D t-1 D t-2 Output layer Figure 16. A three-layer neural network  An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 341 represents the connection weight between output layer and hidden layer. Input layer of the network is a key decision which has a great impact on the effectiveness of the network. Now there is no commonly accepted method for selecting the input layer. In this paper, an all-possible-regression analysis [12,13] is used to define the input layer accord- ing to the R2 P , AIC and CP criterion. It is assumed that input layer is a possible combination from Dt , Dt-1 , Dt-2 , Dt-Dt-1 , Dt-1-Dt-2 , Dt -Dt-2. Purpose of this method is to select a good combination so that a detailed examination can be made of the regression models, leading to the se- lection of the final input vectors to be utilized [12]. The result is shown in Table 1. In light of the R2P, AIC and CP criterion, we select the (Dt, D t-1, D t-2) combination be- cause it has the largest R2P, the smallest AIC and CP val- ues in the Table 1. 3.3 Neural Network Training Based on Genetic Algorithm 1) Determination of fitness function Purpose of which genetic algorithm is used to optimize the network weights and threshold of neural network is to obtain the optimum combination of weights value and threshold. Output error measures the effect of combina- tion. Hence, fitness function of individual chromosome should be the function of output error of BP network. Ideal output value is expressed as Dj and actual output value is expressed as Aj. The fitness function () fE can be written as 2 1 ()(()) (1) jj fEEDA E ==− +∑ (8) 2) Genetic manipulation Assumed that Group size is M and Fitness of individ- ual i is Fi. Individual probability of being selected can be expressed as follows: 1 i si M i i F P F = = ∑ (9) Arithmetic crossover operator is adopted which is spe- cially used to solve floating-point cross, and uniform mutation operator is introduced. 4. Simulation Experiments It is assumed that value of group size M, crossover probability, Mutation probability, training error and gen- eration gap is 100, 0.8, 0.05, 0.005 and 0.7 respectively. To verify the performance of the above method, we make a great deal of simulation experiments on the actual pro- duction. The experiments are divided into three stages. First, 500 “in-control” sample sets (mt=0) and 500 “out-of-control” sample sets (mt≠0), each which involves 200 data points and generated from an AMAR(1,1) noise model, are selected to train the neural network. The 500 out-of-control samples sets perform a process which is upset respectively by step-change with the step of Table 1. R2P, AIC and CP values of all-possible-regression analyse Variables combination P R2P AIC CP Dt 2 0.9212 79.6391 100.9358 Dt-1 2 0.8473 82.5523 682.9437 Dt-2 2 0.5976 85.7604 1259.2257 (Dt,Dt-1) 3 0.8411 81.9853 55.8933 (Dt,Dt-2) 3 0.7952 78.0043 129.4748 (Dt-1,D t-2) 3 0.8319 86.8358 318.4751 (Dt, Dt-1, Dt-2) 4 0.9855 74.2201 3.9241 (Dt,Dt-Dt-1) 3 0.9381 88.9276 18.9937 (Dt,Dt-Dt-1,Dt-1-Dt-2) 4 0.9817 77.0256 5.8619 (Dt-1,D t-1-Dt-2) 3 0.8294 83.9967 53.7724 (Dt-1,D t-Dt-1 ,Dt-1-Dt-2 ) 4 0.9027 79.5720 142.9901 (Dt-2,D t-Dt-2 ) 3 0.8979 80.7342 46.7424 (Dt-2,D t-Dt-1 ,Dt-1-Dt-2 ) 4 0.9145 80.5612 290.0132 (Dt,Dt-1,Dt-1-Dt-2 , Dt-Dt-2) 5 0.9224 78.9267 4.5776 (Dt-1,D t-2,Dt-Dt-1 , Dt-Dt-2) 5 0.9225 78.9399 5.2481 (Dt,Dt-2,Dt-Dt-1, Dt-1 -Dt-2) 5 0.9224 78.9399 5.8932 (Dt,Dt-1,Dt-2,D t-Dt-1 , Dt-Dt-2) 6 0.9224 78.4516 6.9935 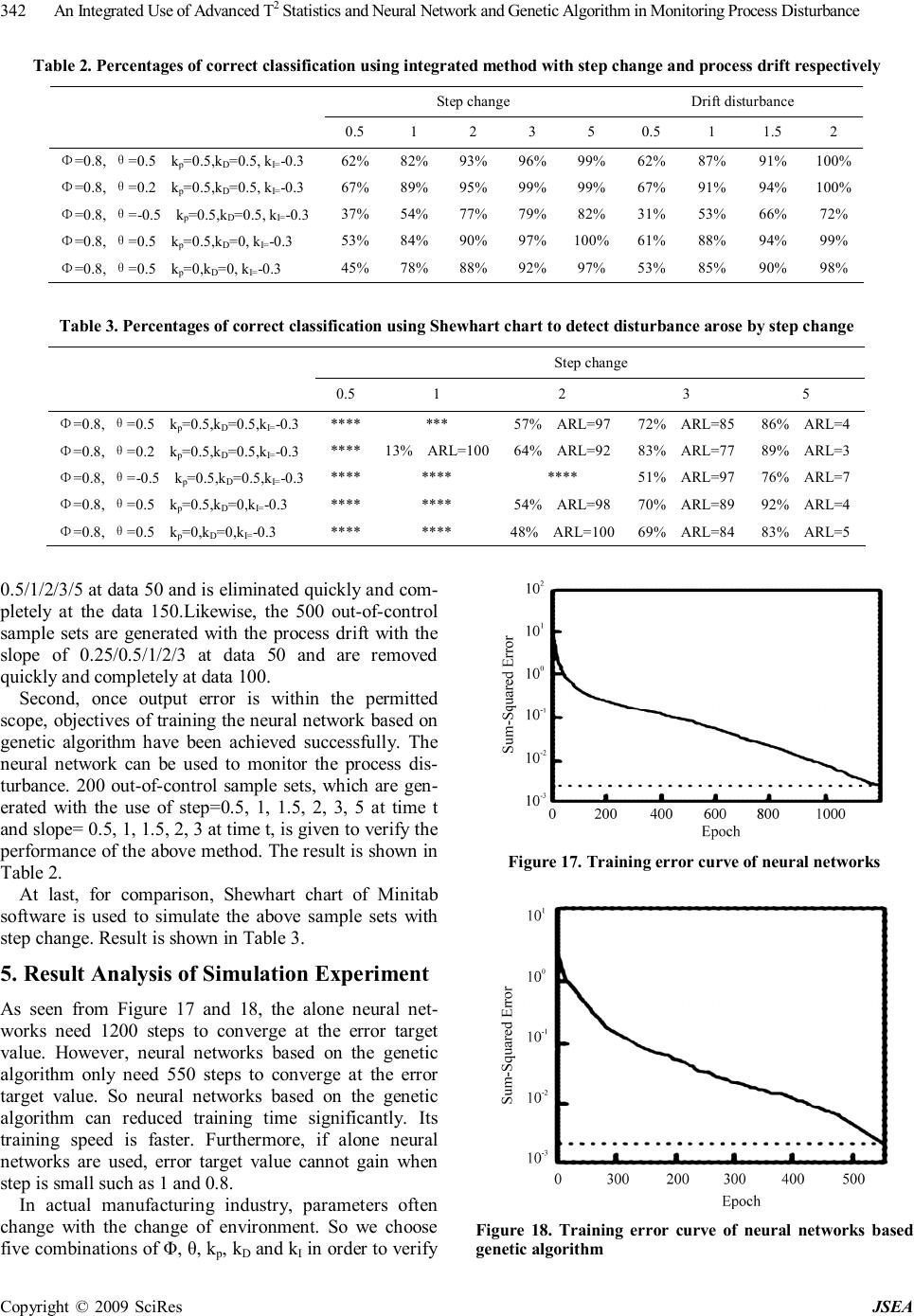 An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 342 Table 2. Percentages of correct classification using integrated method with step change and process drift respectively Step change Drift disturbance 0.5 1 2 3 5 0.5 1 1.5 2 Φ=0.8, θ=0.5 k p =0.5,kD=0.5, kI=-0.3 62% 82% 93% 96% 99% 62% 87% 91% 100% Φ=0.8, θ=0.2 k p =0.5,kD=0.5, kI=-0.3 67% 89% 95% 99% 99% 67% 91% 94% 100% Φ=0.8, θ=-0.5 k p =0.5,kD=0.5, kI=-0.3 37% 54% 77% 79% 82% 31% 53% 66% 72% Φ=0.8, θ=0.5 k p =0.5,kD=0, kI=-0.3 53% 84% 90% 97% 100% 61% 88% 94% 99% Φ=0.8, θ=0.5 k p =0,kD=0, kI=-0.3 45% 78% 88% 92% 97% 53% 85% 90% 98% Table 3. Percentages of correct classification using Shewhart chart to detect disturbance arose by step change Step change 0.5 1 2 3 5 Φ=0.8, θ=0.5 k p =0.5,kD=0.5,kI=-0.3 **** *** 57% ARL=97 72% ARL=85 86% ARL=4 Φ=0.8, θ=0.2 k p =0.5,kD=0.5,kI=-0.3 **** 13% ARL=100 64% ARL=92 83% ARL=77 89% ARL=3 Φ=0.8, θ=-0.5 k p =0.5,kD=0.5,kI=-0.3 **** **** **** 51% ARL=97 76% ARL=7 Φ=0.8, θ=0.5 k p =0.5,kD=0,kI=-0.3 **** **** 54% ARL=98 70% ARL=89 92% ARL=4 Φ=0.8, θ=0.5 k p =0,kD=0,kI=-0.3 **** **** 48% ARL=100 69% ARL=84 83% ARL=5 0.5/1/2/3/5 at data 50 and is eliminated quickly and com- pletely at the data 150.Likewise, the 500 out-of-control sample sets are generated with the process drift with the slope of 0.25/0.5/1/2/3 at data 50 and are removed quickly and completely at data 100. Second, once output error is within the permitted scope, objectives of training the neural network based on genetic algorithm have been achieved successfully. The neural network can be used to monitor the process dis- turbance. 200 out-of-control sample sets, which are gen- erated with the use of step=0.5, 1, 1.5, 2, 3, 5 at time t and slope= 0.5, 1, 1.5, 2, 3 at time t, is given to verify the performance of the above method. The result is shown in Table 2. At last, for comparison, Shewhart chart of Minitab software is used to simulate the above sample sets with step change. Result is shown in Table 3. 5. Result Analysis of Simulation Experiment As seen from Figure 17 and 18, the alone neural net- works need 1200 steps to converge at the error target value. However, neural networks based on the genetic algorithm only need 550 steps to converge at the error target value. So neural networks based on the genetic algorithm can reduced training time significantly. Its training speed is faster. Furthermore, if alone neural networks are used, error target value cannot gain when step is small such as 1 and 0.8. In actual manufacturing industry, parameters often change with the change of environment. So we choose five combinations of Φ, θ, kp, kD and kI in order to verify Figure 17. Training error curve of neural networks Figure 18. Training error curve of neural networks based genetic algorithm  An Integrated Use of Advanced T2 Statistics and Neural Network and Genetic Algorithm in Monitoring Process Disturbance Copyright © 2009 SciRes JSEA 343 the method and cover a reasonable range of the parame- ter space. In terms of the Table 1, the value of parameter Φ, θ has serious impact on the resolution capability of the integrated method. It is very applicable to combine a positive and large Φ with a positive and small θ. On the contrary, the combinations of a positive Φ and a negative θ worsen with the ability to identify the process distur- bance accurately. There is no obvious correlation be- tween change of the controller parameter kp , kD , kI and monitoring ability. With respect to the drift disturbance, step change is easier to be monitored. According to Tables 3 and Table 4, the advantage of the integrated method is significant. The neural network requires only one sample to recognize the disturbance and identify the disturbance type. But Shewhart chart requires an average of 3 to 7 samples to recognize the process disturbance with step 5. When step=2 and 3, an average of 70 to 100 samples are required to detect the disturbance. Even the disturbance with step=1 and 0.5 can not be monitored. 6. Acknowledgments This paper was supported by the grants from National Natural Science Foundation of China (No 70771102), Aviation Science Foundation of China (No. 2007ZG 550050). REFERENCES [1] F. Tsung and D. W. Apley, “The dynamic T 2 chart for monitoring feedback-controlled processes,” IIE Transac- tion, Vol. 34, pp. 1043–1053, 2002. [2] X. H. Wang, G. P. Han, and Q. Q. Li, “A joint-monitor- ing method of process disturbance under an integrated SPC/EPC model, ” Proceedings of the 38th international conference on computers and industrial engineering, Zhengzhou, 2008. [3] C. H. Huang and Y. N. Lin, “Decision rule of assignable causes removal under an SPC/EPC integration system, ” International journal of systems science, Vol. 33, No. 10, pp. 855–867, 2002. [4] D. W. Apley and F. Tsung, “The autoregressive T2 chart for monitoring univariate autocorrelated processes,” Journal of Quality Technology, Vol. 34, No. 1, pp. 79–95, 2002. [5] F. Tsung, “Run to run proportional integral derivative process control and monitoring schemes,” A dissertation submitted in partial fulfillment of the requirements for degree of Doctor of Philosophy, University of Michigan, pp. 121–123, 1997. [6] G. Box and T. Kramer, “Statistical process monitoring and feedback adjustment-a discussion,” American statis- tical Association and the American Society for Quality Control, Journal Technometrics, Vol. 34, No. 3, pp. 251–267, 1992. [7] F. B. Alt, “Multivariate quality control,” in Encyclopedia of the statistical Science, eds. N. L. Johnson, S. Kotz and C. R. Read, New York, John Wiley, pp. 111–122. [8] D. C. Montgomery, J. B. Keats, G. Runger and W. Messina, “Integrating statistical process control and en- gineering process control, ” Journal Quality Technology, Vol. 26, No. 2, pp. 79–87, 1994. [9] H. Hotelling, “Multivariate quality control-illustrated by air testing of sample bombsights,” Techniques of Statis- tical Analysis, Mcgraw-Hill, New York, pp. 11–184, 1947. [10] B. Cheng and D. M. Titterington, “Neural networks: A review from a statistical perspective,” Statistical Science, Vol. 9, pp. 2– 54, 1994. [11] G. D. Feng and C. Chen, “Nonlinear inversion of poten- tial-field data using an improved genetic algorithm, ” Journal of China University of Geosciences, Vol. 15, No. 4, pp. 25–31, 2004. [12] C. C. CHIU, “Identification of process disturbance using SPC/EPC and neural networks,” Journal of intelligent manufacturing, Vol. 14, pp. 379–388, 2003. [13] J. Neter, W. Wasserman, and G. A. Whitmore, Applied Statistics, Boston, Allyn and Bacon, 1979. |

