ABSTRACT

In this paper, using Local Linking Theorem, we obtain the existence of multiple solutions for a class of semilinear elliptic equations with nonlinear boundary conditions, in which the nonlinearites are compared with higher Neumann eigenvalue and the first Steklov eigenvalue.

Keywords:Multiple Solutions; Nonlinear Boundary Conditions; Local Linking Theorem

1. Introduction

In this paper, we investigate the multiple solutions for semilinear elliptic equation with nonlinear boundary conditions

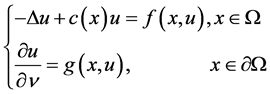(1.1)

where is bounded domain with smooth boundary and is the outward normal derivative on, and the function satisfies C)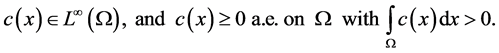

Problems of the above type have been discussed extensively. In 1902, Steklov (see [1]) studied the eigenvalue problem

(1.2)

Auchmuty (see [2]) considered the eigenvalue problem

(1.3)

where satisfies the condition C) and proved that the eigenfunctions provide a complete orthonormal bases of certain closed subspace of. Using sub and super-solutions method, Amann (see [3]), Mawhin and Schmitt (see [4]) obtained some existence results for the problem (1.1). However, since it is based on comparison techniques, the sub and super-method does not apply when the nonlinearities are compared with higher eigenvalues.

In this paper, using the Local Linking Theorem, we obtain multiple solutions for the problem (1.1), which the nonlinearites are compared with higher Neumann eigenvalue and the first Steklov eigenvalue.

2. Preliminaries and Main Results

Let denote the Lebesgue space with the norm, and with the norm

. Obviously, the space and the space inner product are denoted by

.

is a Hilbert space under the standard inner product

(2.1)

with the associated norm. As the function satisfies the condition C), we define the weighted inner product by

(2.2)

and the associated norm. By Corollary 3.3 in [2], we obtain that the norm is equivalent to the standard norm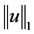. As the function satisfies the condition C), by Equation (2.2), we can split

as a direct orthogonal sum.

Now, we state the Local Linking theorem introduced by [5].

Lemma 2.1 Let is a reflexive Banach space, with satisfies the (PS) condition, if 1) there exists a constant such that

,

2) is bounded below and then the functional has at least two nontrivial critical points.

Proof. See Theorem 4 in [5].

For the problem (1.3), Auchmuty (see [2]) obtained that

holds for all, where is the first Steklov eigenvalue for the problem (1.3). In [6], for the Neuman eigenvalue problem

they obtain that the above problem has a sequence of real eigenvalues

(2.3)

with finite dimensional eigenspaces.

Assume that, , are Carathedory functions satisfying H1) There exist and 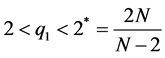such that

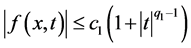for all and for a.e.

H2) There exist and such that

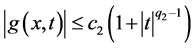for all and for a.e.

H3) There exist 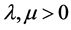such that

and

uniformly for with

.

H4) There exist a integer 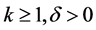and four constants such that

uniformly for, , where

Theorem 2.2 Suppose satisfies C), and H1)-H4) hold, Then the problem (1.1) has at least two distinct nontrivial solutions.

3. The Proofs of Theorem 2.2

Now, we define the functional

(3.1)

where

Since the function satisfies H1), satisfies H2), by the Sobolev embedding of

into, the continuity of the trace operator from into and the Holder inequalitywe obtain that the functional 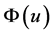is well defined. Moreover, by Lemma 2.1, and Lemma 4.2 in [7], we obtain that, and

(3.2)

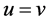Furthermore, the functional is weakly continuous, and is compact. Let in (3.2) and a simple computation, we obtain that the critical point of the functional is the weak solution of the problem (1.1).

Lemma 3.1 (see [7]) Assume that the function satisfies the condition C), H1) and H2) hold. If 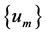is a (PS) sequence for the functional, and is bounded in then has a strongly convergence subsequence. i.e. satisfies the (PS) condition.

Lemma 3.2 Assume that satisfies the condition C), and H1)-H3) hold, the functional is coercive on

Proof By H3), we obtain that there exist some constants 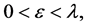and, such that

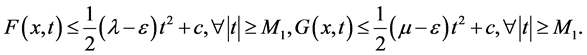(3.3)

From H1), H2) and Equation (3.3), we obtain that there exist such that

, (3.4)

Hence, we obtain that

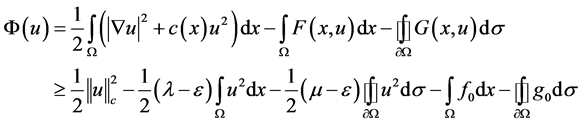(3.5)

Assume that then using the continuity of the trace operator from into, we obtain either or where is a positive constant.

Case 1 As by Equation (3.5), we obtain

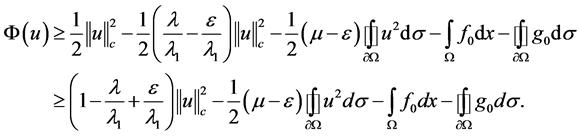
Hence, we obtain that is coercive on since.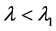

Case2 As we have

.

By H3), we obtain, then 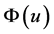is coercive on.

Hence we obtain that the functional is bounded from below, and every (PS) sequence is bounded in. From Lemma 3.1, we obtain that satisfies (PS) condition and is bounded from below.

The Proof of Theorem 2.2 We write, where

and.

Hence, we have

.

Since is a finite dimensional space, by [2], we obtain that for given there is a such that

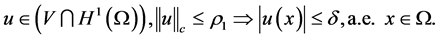
Hence, for each, by H4), we have

We have for sufficiently small,

.

Therefore, we obtain that.

On the other hand, let and then for every with, by H4), we obtain that

. (3.6)

Combining Equation (3.4), Equation (3.6), H1) and H2), we have

From Equation (2.6), we have, for sufficiently small

Since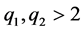, we can choose sufficiently small and, , such that the functional.

By Lemma 3.2, we obtain that 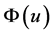satisfies (PS) condition and is bounded from below. If

then by Lemma 2.1, possesses two nonzero critical point. From (3.3), we obtain that there exist two nontrivial weak solutions for the problem (1.1).

4. Conclusion

Using Local Linking Theorem, we obtain the existence of two nontrival weak solutions for the problem (1.1) which the nonlinearites and are compared with higher Neumann eigenvalue and the first Steklov eigenvalue.

Acknowledgements

This paper was supported by Shanghai Natural Science Foundation Project (No. 11ZR1424500) and Shanghai Leading Academic Discipline Project (No. XTKX2012).

REFERENCES