Wireless Engineering and Technology
Vol.2 No.2(2011), Article ID:4549,5 pages DOI:10.4236/wet.2011.22015
A Self-Similar Fractal Cantor Antenna for MICS Band Wireless Applications*
![]()
1Department of Electronics and Communication Engineering, PSG College of Technology, Coimbatore, India; 2Department of Mathematics, PSG College of Technology, Coimbatore, India.
Email: srivatsunece@yahoo.co.in, ssrece@psgtech.ac.in
Received October 26th, 2010; revised February 14th, 2011; revised February 16th, 2011.
Keywords: Fractal antenna, multicantor, self-similar antenna, MICS, ISM, wideband, return loss, Wireless
ABSTRACT
Low profile antenna in communication is a new methodology. Fractal geometry is a methodology through which size reduction is achieved. A Self-similar fractal antenna using multicantor technique is proposed and experimentally studied. Space-filling cantors and self-similarity properties of fractal geometry have been adopted in the proposed antenna to miniaturize the size of antenna. The antenna is designed in such a way to operate at MICS band (Medical Implant communication Service) for wireless telemedicine application. The prototype antenna exhibits wideband characteristics and provides a good agreement of return loss (S11). Experimental return loss has been compared with that which is obtained using method of moments. The objective of using self-similar concept in antenna makes it flexible in terms of controlling the resonance and bandwidth. In this paper, the Self-similar property of fractal geometry is examined by maintaining return loss (S11) more than –30 dB approximately in all the iterations (n) and the prototype antenna has return loss greater than –10 dB and exhibits wideband characteristics.
1. Introduction
The increase in growth of wireless systems and the demand in wireless telemedicine applications in health care and patient monitoring system is increasing day by day. To monitor patients at remote area and to provide better healthcare by transmitting physiological and pathology parameters through wireless, fractal antennas on microstrip platform is a solution for wireless boards. These fractal antennas on wireless boards can enhance serve for transmission and occupy less space. The MICS (Medical Implant Communication Service) band with 400 - 405 MHz has been allocated for medical and metrological applications and 2400 MHz ISM (Indian Scientific and Medical band) has been especially allocated for biomedical applications. The self-similarity property of fractal geometry and a number of new antenna designs have been reported in the literature.
A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole, and this property is called self-similarity. Fractals [1] geometries are composite designs that repeat themselves or their statistical characteristics and are thus “self similar”. Fractal geometry finds a variety of application in engineering. All structures in nature can be implemented as fractal [2]. Fractal geometry is space filling cantors of regular and irregular shapes [2-13], and is super imposed of too much iteration and they describe the self-similar property of fractal geometry. When the fractal iteration factor is 2.5, then the original patch gets reduced by 45% in size, thereby maintaining a radiation pattern comparable to that of a normal patch [14]. A self similar [3] structure is that which is scaled down by itself to a maximum number of possible iterations (n) and because of this, the size of the geometry shrinks down along its length and width by retaining its originality.
A Self-affine [3] structure shrinks down by diverse factors, and this provides flexibility in designing miniaturized planar antenna. By selecting appropriate scaling factors and optimizing the feed position, the antenna resonates for more than one frequency. Sinha and Jain [15] examined Self-affine property of fractals and evaluated it for multiband characteristics and implemented using a microstrip feed line.
2. Design Procedure
2.1. Proposed Self-Similar Technique
The self-similar fractal structures are constructed by scaling a rectangle i.e., the initiator M0 Figure 1(a), by a factor of three along its x and y coordinates, i.e., three along its length and its width, which leads to six rectangles on the upper half, middle and lower planes, the obtained rectangles measure equal in dimension. The left and right columns are eliminated except the middle region as shown in Figure1(b). Initially, the initiator M0 is made to resonate at design frequency 405MHz by adopting coaxial feed technique at 145 mm × 50 mm. This process is a repetitive procedure and is continued upto nth iteration. Figures 1(c) to Figure 1(d) show that the number of iterations undergone by the initiator M0.
In the above self-similar fractal structure, the segments are developed at each iteration of same dimensions. The antenna design on these concepts tends to reduce in size and occupies less space.
2.2. Antenna Design
The self–similar antenna structure is developed on a FR4 substrate (thickness 1.6 mm, εr = 4.4, tan δ = 0.01) with ground plane at the bottom of the substrate. The patch antenna is initially started with (M0) of dimensions 223 mm × 174 mm × 1.6 mm which resonates at 405 MHz. Then, the initiator is iterated into segments, and the generator of (M1) to (M3) as shown in Figure 1. According to the property of self-similarity, the fractal dimension of the set 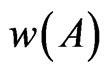 contains nine subsets, the iterative coefficients for the sets are derived as follows.
contains nine subsets, the iterative coefficients for the sets are derived as follows.

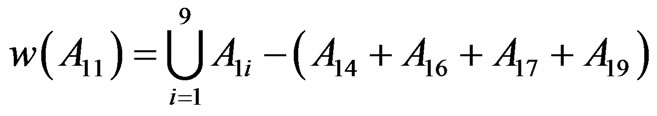




Similarly w(A21…A25), w(A31…A35) and w(A51…A55). The fractal dimension D of the set 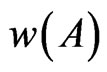 is given as
is given as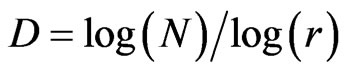 , N is the total number of distinct copies similar to A, and scaled down by a ratio of 1/r. For the proposed design D = 1.465.
, N is the total number of distinct copies similar to A, and scaled down by a ratio of 1/r. For the proposed design D = 1.465.
 (a)
(a)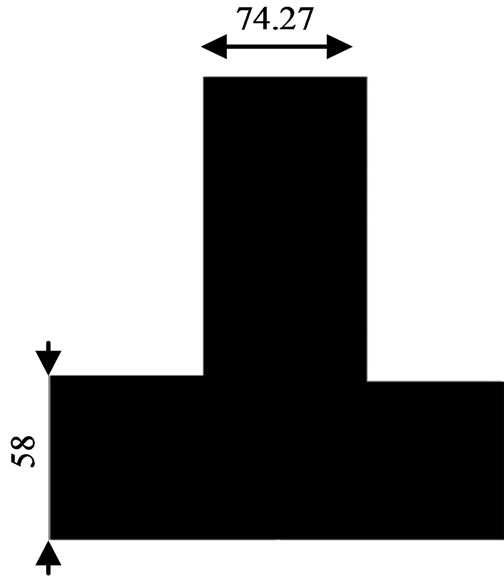 (b)
(b) (c)
(c) (d)
(d)
Figure 1. Self-similiar fractal structure. (a) Initiator M0; (b) First iteration M1; (c) Second iteration M2; (d) Third iteration M3.
The performance of the antenna at different iteration has been investigated using ADS momentum. The resonant behavior of self-similar antenna is shown in Figure 2. The initial patch antenna resonates nearby 403 MHz [16]. The feed position is optimized to resonate at design frequency in all the iterations to achieve maximum return loss. As iteration (n) increases, the number of ladder like projections increases at the centre. The ladders generate the other resonant modes; the resonating bands are dependent on the ground plane. The resonant frequencies of the proposed self-similar structure are listed in Table 1. The measured return loss (S11) of the self-similar structure is found to exhibit wideband characteristics starting from 390 MHz to 420 MHz with a maximum of –35 dB return loss and bandwidth 30 MHz with reference as –10 dB. The Initiator (M0) resonates at 403 MHz with –41 dB405 MHz, 404.6 MHz and 403 MHz frequencies with return loss of –15 dB, –35.5 dB, –40 dB respectively iterations M1, M2 and M3. The proposed self-similar antenna was etched on a FR4 substrate with the above specifications (section B) with eight portion of ferric chloride and 2 portion of dilute hydrochloric acid. Figure 3 reveals the prototype model of the self-similar structure. Figure 4 depicts the measured return loss (S11) of the self-similar structure using agilent network analyzer. Figure 5 depicts the simulated radiation pattern for Ecross polarization and co-polarization at 403 MHz, the antenna is linearly and circularly polarized, so it fits for multiband wireless applications. The authors were limited only to scope measurements. The gain of the antenna is found to be 8.91 dBi.
 (a)
(a) (b)
(b) (c)
(c)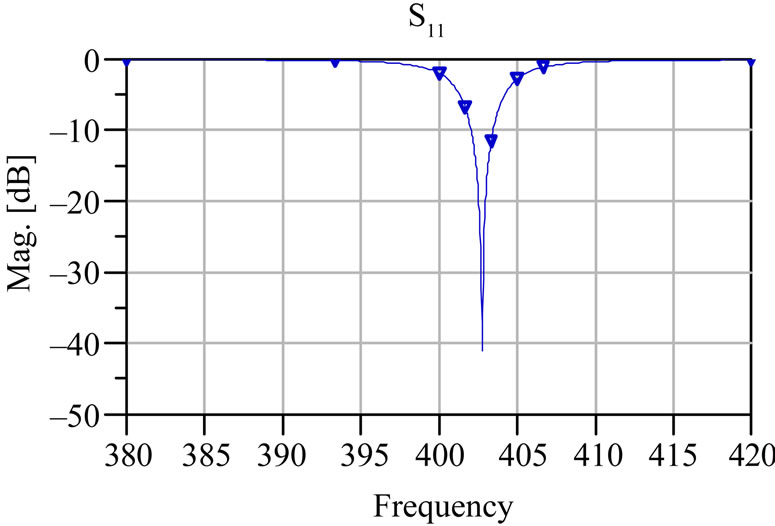 (d)
(d)
Figure 2. Simulated return loss (S11) of the self-similar structure (a) initiator M0; (b) First iteration M1; (c) Second iteration M2; (d) Third iteration M3.

Table 1. Simulated return loss at various iterations for a self-similar fractal antenna.

Figure 3. Prototype of the self-similiar fractal antenna.

Figure 4. Measured return loss (S11) of the self-similar structure.

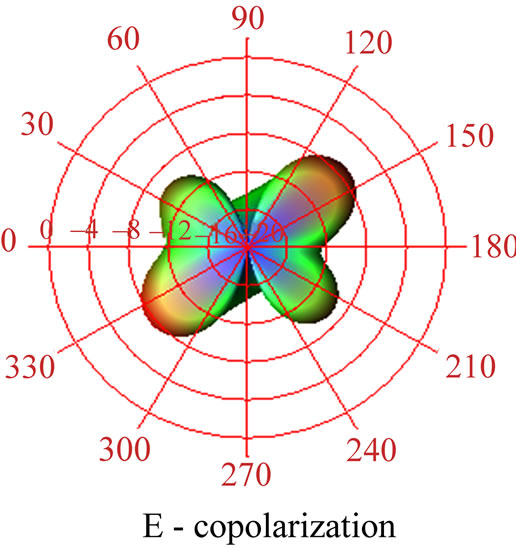
Figure 5. Simulated radiation pattern (S11) of the self-similar structure for 403 MHz.
3. Conclusions
A low profile, low cost self-similar antenna, which is developed to operate in 402 - 405 MHz, is found to provide a wide bandwidth. The return loss (S11) of the self-similar antenna is maintained for more than –35 dB except iteration (M1). Therefore the proposed antenna can be incorporated in any wireless telemedicine boards or through handheld devices for monitoring the physiological parameters and to effectively transmit the collected data. As the antenna exhibits wideband characteristics, it can be used in a variety of application. The performance of the prototype was tested using rabbit processor GSM module by detaching the dipole antenna, and the prototype model was attached, the patient health records such as body temperature, pulse and respiration were collected through modules and transmitted through the prototype and found that transfer of data provides good agreement.
REFERENCES
- B. Mandelbrot, “Fractals: Form, Chance, and Dimension,” W.H. Freeman and Company, San Francisco, 1997.
- M. F. Barnsley, “Fractals Everywhere,” 2nd Edition, Academic Press, San Diego, 1993.
- H. O. Peitgen, H. Jurgens and D. Saupe, “Chaos and Fractals,” New Frontiers in Science, Springer-Verlag, New York, 1992.
- C. Punente, J. Romeu, R. Pous, X. Garcia and F. Benitez, “Fractal Multiband Antenna Based on the Sierpinski Gasket,” Electronic Letters, Vol. 32, No. 1, January 1996, pp. 1-2. doi:10.1049/el:19960033
- J. P. Gianvittoria and Y. Rahmat-Samii, “Fractal Antennas: A Novel Antenna Miniaturization Technique, and Applications,” IEEE Antennas and Propagation Magazine, Vol. 44, No. 1, February 2002, pp. 20-36. doi:10.1109/74.997888
- D. H. Werner and S. Ganguly, “An Overview of Fractal Antenna Engineering Research,” IEEE Antennas and Propagation Magazine, Vol. 45, No. 1, February 2003, pp. 38-57. doi:10.1109/MAP.2003.1189650
- K. J. Vinoy, “Fractals Shaped Antenna Elements for Wide Band Multiband Wireless Applications,” Ph.D., Dissertation, Department of Electrical Engineering, Pennsylvania State University, University Park, 2002.
- J. C. Liu, C. Y. Wu, D. C. Chang and C. Y. Liu, “Relationship between Sierpenski Gasket and Apollonian Packing Monopole Antennas,” Electronics Letters, Vol. 42, No. 15, July 2006, pp. 847-848. doi:10.1049/el:20061123
- T. K. Lo and Y. Hwang, “Microstrip Antennas of Very High Permittivity for Personal Communications,” Proceedings of Asia Pacific Microwave Conference, Hong Kong, 2-5 December 1997, pp. 253-256.
- R. A. Sainati, “CAD of Microstrip Antennas for Wireless Applications,” Artech House, Norwood, 1996.
- H. Y. Wang and M. J. Lancaster, “Aperture-Coupled Thin-Film Superconducting Meander Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 47, No. 5, 1999, pp. 829-836. doi:10.1109/8.774137
- P. E. Mayes, “Frequency-Independent Antenna and BroadBand Derivatives thereof,” Proceedings of IEEE, Vol. 80, No. 1, 1992, pp. 103-112. doi:10.1109/5.119570
- C. Puente, J. Romeu, R. Pous and A. Carma, “On the Behaviour of the Sierpinski Multiband Fractal Antenna,” IEEE Transactions on Antennas and Propagation, Vol. 46, No. 4, 1998, pp. 517-524. doi:10.1109/8.664115
- I.-K. Kim, J.-G. Yook and H.-K. Park, “Fractal-Shape Small Size Microstrip Patch Antenna,” Microwave and Optical Technology Letters, Vol. 34, No. 1, July 2002, pp. 15-17. doi:10.1002/mop.10359
- S. N. Sinha and M. Jain, “A Self-Affine Fractal Multiband Antenna,” IEEE Antennas Wireless Propagation Letters, Vol. 6, No. 11, 2007, pp. 110-112. doi:10.1109/LAWP.2007.891519
- G. Kumar and K. P. Ray, “Broadband Microstrip Antenna,” Artech House, Norwood, 2003.
NOTES
*This work was supported by Agilent–Multipurpose lab Station, PSG College of Technology, Coimbatore, India.

