ABSTRACT

In this paper, we investigate the solvability of a class of semilinear elliptic equations which are perturbation of the problems involving critical Hardy-So- bolev exponent and Hardy singular terms. The existence of at least a positive radial solution is established for a class of semilinear elliptic problems involving critical Hardy-Sobolev exponent and Hardy terms. The main tools are variational method, critical point theory and some analysis techniques.

Keywords:

Hardy Singular Terms, Hardy-Sobolev Exponent, Positive Radial Solution, Perturbation Method, Variational Approach

1. Introduction and Main Results

In this paper, we are concerned with the existence of positive radial solutions for the following semilinear elliptic problem with Hardy-Sobolev exponent and Hardy singular terms:

$\{\begin{array}{ll}-\Delta u-\mu \frac{u}{{\left|x\right|}^2}=\left[1+\delta h\left(\left|x\right|\right)\right]\frac{{\left|u\right|}^{2^{\ast }\left(s\right)-2}}{{\left|x\right|}^s}u,\hfill & x\in {ℝ}^N\hfill \\ u>0,\hfill & x\in {ℝ}^N\hfill \\ u\in D_r^{1,2}\left({ℝ}^N\right)=\left\{u\in D^{1,2}\left({ℝ}^N\right):u\text{is}\text{radial}\right\},\hfill & \hfill \end{array}$ (1.1)

where $0<s<2,2^{*}\left(s\right)=\frac{2\left(N-s\right)}{N-2}$ is the Hardy-Sobolev critical exponent and $2^{*}=2^{*}\left(0\right)=\frac{2N}{N-2}$ is the Sobolev critical exponent, $\mu <\bar{\mu }\triangleq \frac{{\left(N-2\right)}^2}{4}$ . $D^{\mathrm{1,2}}\left({ℝ}^N\right)\left(N\ge 3\right)$ denotes the space of the functions $u\in L^{2^{\ast }}\left({ℝ}^N\right)$ such that $\nabla u\in L^2\left({ℝ}^N\right)$ , endowed with scalar product and norm, respectively, given by

$\begin{array}{l}\langle u,v\rangle ={\displaystyle {\int }_{{ℝ}^N}}\left(\nabla u\cdot \nabla v-\mu \frac{uv}{{\left|x\right|}^2}\right)\text{d}x,\\ {\Vert u\Vert }^2={\displaystyle {\int }_{{ℝ}^N}}\left({\left|\nabla u\right|}^2-\mu \frac{u^2}{{\left|x\right|}^2}\right)\text{d}x,\end{array}$

that coincides with the completion of $C_0^{\infty }\left({ℝ}^N\right)$ with respect to the L²-norm of the gradient. By Hardy inequality [1] , we easily derive that the norm is equivalent to the usual norm:

${\Vert u\Vert }_0^2={\displaystyle {\int }_{{ℝ}^N}}{\left|\nabla u\right|}^2\text{d}x$

in $D^{\mathrm{1,2}}\left({ℝ}^N\right)$ .

Clearly, $D_r^{\mathrm{1,2}}\left({ℝ}^N\right)$ is a closed subset of $D^{\mathrm{1,2}}\left({ℝ}^N\right)$ , so $D_r^{\mathrm{1,2}}\left({ℝ}^N\right)$ is a Hilbert space. By the symmetric criticality principle, in view of [2] , we know that the positive radial solutions of problem (1.1) correspond to the nonzero critical points of the functional $I_{\delta }\mathrm{<mo>\; :\; </mo>}{D}_r^{\mathrm{1,2}}\left({ℝ}^N\right)\to ℝ$ defined by

$\begin{array}{c}{I}_{\delta }\left(u\right)=\frac{1}{2}{\displaystyle {\int }_{{ℝ}^N}}\left({\left|\nabla u\right|}^2-\mu \frac{u^2}{{\left|x\right|}^2}\right)\text{d}x-\frac{1}{2^{\mathrm{<mo>\; *\; </mo>}}\left(s\right)}{\displaystyle {\int }_{{ℝ}^N}}\frac{{\left|u^{+}\right|}^{2^{\mathrm{<mo>\; *\; </mo>}}\left(s\right)}}{{\left|x\right|}^s}\text{d}x\\ -\frac{\delta }{2^{\mathrm{<mo>\; *\; </mo>}}\left(s\right)}{\displaystyle {\int }_{{ℝ}^N}}h\left(\left|x\right|\right)\frac{{\left|u^{+}\right|}^{2^{\mathrm{<mo>\; *\; </mo>}}\left(s\right)}}{{\left|x\right|}^s}\text{d}x\mathrm{,}\end{array}$

where $u^{+}=\max \left\{u,0\right\}$ .

The reason why we investigate (1.1) is the presence of the Hardy-Sobolev exponent, the unbounded domain ${ℝ}^N$ and the so-called inverse square potential in the linear part, which cause the loss of compactness of embedding $D^{\mathrm{1,2}}\left({ℝ}^N\right)\to L^{2^{\mathrm{<mo>\; *\; </mo>}}}\left({ℝ}^N\right)$ , $H^1\left({ℝ}^N\right)\to L^p\left({ℝ}^N\right)$ and $D^{\mathrm{1,2}}\left({ℝ}^N\right)\to L^2\left({\left|x\right|}^{-2}\text{d}x\right)$ . Hence, we face a type of triple loss of compactness whose interacting with each other will result in some new difficulties. In last two decades, loss of compactness leads to many interesting existence and nonexistence phenomena for elliptic equations. There are abundant results about this class of problems. For example, by using the concentration compactness principle, the strong maximum principle and the Mountain Pass lemma, Li et al. [3] had obtained the existence of positive solutions for singular elliptic equations with mixed Dirichlet-Neumann boundary conditions involving Sobolev-Hardy critical exponents and Hardy terms. Bouchekif and Messirdi [4] obtained the existence of positive solution to the elliptic problem involving two different critical Hardy-Sobolev exponents at the same pole by variational methods and concentration compactness principle. Lan and Tang [5] have obtained some existence results of (1.1) with $\mu =0$ via an abstract perturbation method in critical point theory. There are some other sufficient conditions, we refer the interested readers to ( [6] - [18] ) and the references therein.

In the present paper, we investigate the existence of positive radial solutions of problem (1.1). There are several difficulties in facing this problem by means of variational methods. In addition to the lack of compactness, there are more intrinsic obstructions involving the nature of its critical points. Based on a suitable use of an abstract perturbation method in critical point theory discussed in [5] [13] [14] , we show that the semilinear elliptic problem with Hardy-Sobolev exponent and Hardy singular terms has at least a positive radial solution.

In this paper, we assume that h satisfies one of the following conditions:

(H) $h\in L^{\infty }\left({ℝ}^N\right)\cap C^1\left({ℝ}^N\right),h\left(x\right)=h\left(\left|x\right|\right)=h\left(r\right),r=\left|x\right|$ , and

${\displaystyle {\int }_1^{\infty }}{r}^{-\alpha +N-s-1}h\left(r\right)\text{d}r<\infty$

for some $\alpha <N-s$ .

(H’) $h\in C^2\left({ℝ}^N\right),h\left(x\right)=h\left(\left|x\right|\right)=h\left(r\right),r=\left|x\right|$ , $h\left(r\right)$ is T-periodic and

${\displaystyle {\int }_0^T}h\left(r\right)\text{d}r=0.$

The main results read as follows.

Theorem 1 Let (H) hold, and assume that $h\left(0\right)=0$ and $h\cancel{\equiv }0$ . Then for $\left|\delta \right|$ small, problem (1.1) has a positive radial solution $u_{\delta }$ .

Remark 1 It is easy to check that the following function $h\left(r\right)$ satisfies the conditions of Theorem 1,

$h\left(r\right)=\frac{2r}{{\text{e}}^r}.$

Theorem 2 If assumption (H) holds, and suppose that $h\in C^2\left({ℝ}^N\right)$ and $h\left(0\right)h^{″}\left(0\right)>0$ . Then for $\left|\delta \right|$ small, problem (1.1) has a positive radial solution $u_{\delta }$ .

Remark 2 It is easy to check that the following function $h\left(r\right)$ satisfies the conditions of Theorem 2,

$h\left(r\right)=\frac{1-2r}{{\text{e}}^r}.$

Theorem 3 Assume that (H) holds, and suppose

${\displaystyle {\int }_0^{\infty }}h\left(r\right){\left(1+r^{2-s}\right)}^{-\frac{2\left(N-s\right)}{2-s}}{r}^{N-s-1}\text{d}r\ne 0$

and ${\displaystyle {\int }_0^{\infty }}h\left(0\right)h\left(r\right){\left(1+r^{2-s}\right)}^{-\frac{2\left(N-s\right)}{2-s}}{r}^{N-s-1}\text{d}r\le 0.$

Then for $\left|\delta \right|$ small, problem (1.1) has a positive radial solution $u_{\delta }$ .

Remark 3 It is easy to check that the following function $h\left(r\right)$ satisfies the conditions of Theorem 3 for all $N\ge 3$ and $0<s<2$ ,

$h\left(r\right)=\frac{r}{{\text{e}}^r},$

in fact,

${\displaystyle {\int }_0^{\infty }}h\left(r\right){\left(1+r^{2-s}\right)}^{-\frac{2\left(N-s\right)}{2-s}}{r}^{N-s-1}\text{d}r\ne 0$

and ${\displaystyle {\int }_0^{\infty }}h\left(0\right)h\left(r\right){\left(1+r^{2-s}\right)}^{-\frac{2\left(N-s\right)}{2-s}}{r}^{N-s-1}\text{d}r=0;$

We can also give the following example for $N=3$ and $s=1$ ,

$h\left(r\right)=\frac{1-100r}{{\text{e}}^r},$

in fact, with the help of computers, we can get

${\displaystyle {\int }_0^{\infty }}\frac{1-100r}{{\text{e}}^r}{\left(1+r^{2-1}\right)}^{-\frac{2\left(3-1\right)}{2-1}}{r}^{3-1-1}\text{d}r\approx -4.06\ne 0$

and ${\displaystyle {\int }_0^{\infty }}h\left(0\right)\frac{1-100r}{{\text{e}}^r}{\left(1+r^{2-1}\right)}^{-\frac{2\left(3-1\right)}{2-1}}{r}^{3-1-1}\text{d}r\approx -4.06<0.$

Theorem 4 Suppose that assumption (H’) holds, and satisfies the condition that $h\left(0\right)h^{″}\left(0\right)>0$ . Then problem (1.1) has a positive radial solution $u_{\delta }$ , provided $\left|\delta \right|\ll 1$ .

Remark 4 It is easy to check that the following function $h\left(r\right)$ satisfies the conditions of Theorem 4,

$h\left(r\right)={\text{e}}^{\sin \left(\frac{\text{7π}}{4}+r\right)}\cos \left(\frac{7\text{π}}{4}+r\right),$

in fact,

$h\left(0\right)={\text{e}}^{\sin \left(\frac{\text{7π}}{4}+0\right)}\cos \left(\frac{7\text{π}}{4}+0\right)=\frac{\sqrt{2}}{2}{\text{e}}^{-\frac{\sqrt{2}}{2}}>0,$

and by a direct computation, we have

$h^{″}\left(0\right)=\sqrt{2}{\text{e}}^{-\frac{\sqrt{2}}{2}}>0.$

Theorem 5 Let h satisfy (H’), and suppose that $h\left(0\right)=0$ and $h\cancel{\equiv }0$ . Then problem (1.1) has a positive radial solution $u_{\delta }$ , provided $\left|\delta \right|\ll 1$ .

Remark 5 It is easy to check that the following function $h\left(r\right)$ satisfies the conditions of Theorem 5,

$h\left(r\right)=\sin 2r.$

This paper is organized as follows. After a first section we devoted to studying

the unperturbed problem $-\Delta u-\mu \frac{u}{{\left|x\right|}^2}=\frac{{\left|u\right|}^{2^{\ast }\left(s\right)-2}}{{\left|x\right|}^s}u$ . The main results are proved

in Section 3. In the following discussion, we denote various positive constants as

C or $C_i\left(i=\mathrm{0,1,2,3,}\cdots \right)$ for convenience. $o\left(t\right)$ denote $\frac{o\left(t\right)}{t}\to 0$ as $t\to 0^{+}$ .

This idea is essentially introduced in [5] [13] .

2. The Case $\delta =0$

In this section, we will study the unperturbed problem

$\{\begin{array}{ll}-\Delta u-\mu \frac{u}{{\left|x\right|}^2}=\frac{{\left|u\right|}^{2^{*}\left(s\right)-2}}{{\left|x\right|}^s}u,\hfill & x\in {ℝ}^N;\hfill \\ u\in D_r^{1,2}\left({ℝ}^N\right),u>0,\hfill & x\in {ℝ}^N.\hfill \end{array}$ (2.1)

It is well-known that the nontrivial solutions of problem (2.1) are equivalent to the nonzero critical points of the energy functional

$I_0\left(u\right)=\frac{1}{2}{\displaystyle {\int }_{{ℝ}^N}}\left({\left|\nabla u\right|}^2-\mu \frac{u^2}{{\left|x\right|}^2}\right)\text{d}x-\frac{1}{2^{*}\left(s\right)}{\displaystyle {\int }_{{ℝ}^N}}\frac{{\left|u^{+}\right|}^{2^{*}\left(s\right)}}{{\left|x\right|}^s}\text{d}x,u\in D_r^{1,2}\left({ℝ}^N\right).$

Obviously, the energy functional $I_0\left(u\right)$ is well-defined and is of $C^2$ with derivatives given by

$\langle {I^{\prime }}_0\left(u\right),v\rangle ={\displaystyle {\int }_{{ℝ}^N}}\left(\nabla u\cdot \nabla v-\mu \frac{uv}{{\left|x\right|}^2}\right)\text{d}x-{\displaystyle {\int }_{{ℝ}^N}}\frac{{\left|u^{+}\right|}^{2^{*}\left(s\right)-1}}{{\left|x\right|}^s}v\text{d}x,u,v\in D_r^{1,2}\left({ℝ}^N\right);$

$\begin{array}{l}\langle {I^{″}}_0\left(u\right)v,w\rangle ={\displaystyle {\int }_{{ℝ}^N}}\left(\nabla v\cdot \nabla w-\mu \frac{vw}{{\left|x\right|}^2}\right)\text{d}x-{\displaystyle {\int }_{{ℝ}^N}}\frac{\left(2^{*}\left(s\right)-1\right){\left|u^{+}\right|}^{2^{*}\left(s\right)-2}}{{\left|x\right|}^s}vw\text{d}x\\ u,v,w\in D_r^{1,2}\left({ℝ}^N\right).\end{array}$

For all $\epsilon >0$ , it is well known that the function

$z_{\epsilon }\left(r\right)={\left(\frac{2{\epsilon }^{\frac{\left(2-s\right)\sqrt{\bar{\mu }-\mu }}{\sqrt{\bar{\mu }}}}\left(N-s\right)\left(\bar{\mu }-\mu \right)}{\sqrt{\bar{\mu }}}\right)}^{\frac{\sqrt{\bar{\mu }}}{2-s}}/\left(r^{\sqrt{\bar{\mu }}-\sqrt{\bar{\mu }-\mu }}{\left({\epsilon }^{\frac{\left(2-s\right)\sqrt{\bar{\mu }-\mu }}{\sqrt{\bar{\mu }}}}+r^{\frac{\left(2-s\right)\sqrt{\bar{\mu }-\mu }}{\sqrt{\bar{\mu }}}}\right)}^{\frac{N-2}{2-s}}\right)$

solves the equation (2.1) and satisfies

${\displaystyle {\int }_{{ℝ}^N}}\left({\left|\nabla z_{\epsilon }\right|}^2-\mu \frac{z_{\epsilon }^2}{{\left|x\right|}^2}\right)\text{d}x={\displaystyle {\int }_{{ℝ}^N}}\frac{{\left|z_{\epsilon }\right|}^{2^{*}\left(s\right)}}{{\left|x\right|}^s}\text{d}x.$

Let

$U\left(r\right)={\left(\frac{2\left(N-s\right)\left(\bar{\mu }-\mu \right)}{\sqrt{\bar{\mu }}}\right)}^{\frac{\sqrt{\bar{\mu }}}{2-s}}/\left(r^{\sqrt{\bar{\mu }}-\sqrt{\bar{\mu }-\mu }}{\left(1+r^{\frac{\left(2-s\right)\sqrt{\bar{\mu }-\mu }}{\sqrt{\bar{\mu }}}}\right)}^{\frac{N-2}{2-s}}\right)\mathrm{,}$

then

$z_{\epsilon }\left(r\right)={\epsilon }^{-\frac{N-2}{2}}U\left(\frac{r}{\epsilon }\right).$

$I_0$ has a (non-compact) 1-dimensional critical manifold given by

$Z=\left\{z=z_{\epsilon }\left(r\right):\epsilon >0\right\}.$

The unperturbed problem is invariant under the transformation that

transforms the function $u\left(r\right)$ in the function ${\epsilon }^{-\frac{N-2}{2}}u\left(\frac{r}{\epsilon }\right)$ . The purpose of this

section is to show the following lemmas.

Lemma 2.1. For all $\epsilon >0$ , $T_{z_{\epsilon }}Z=\text{Ker}\left[{I^{″}}_0\left(z_{\epsilon }\right)\right]$ .

Proof. We will prove the lemma by taking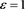, hence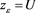. The case of a general 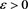will follow immediately. It is always true that 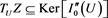. We will show the converse, i.e., that if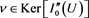, namely is a solution of

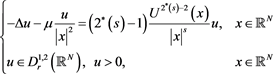(2.2)

then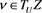, namely such that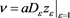, where 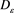denotes the

derivatives with respect to the parameter. We look for solutions 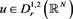of problem (2.2). One has

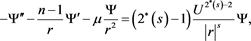
and then a first solution is given by

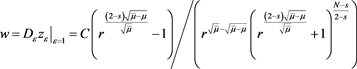
which belongs to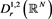, where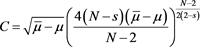. If we

look for a second independent solution of the form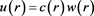, we will check that u is not in. A direct computation gives

and because is a solution, we have

Setting, we obtain

namely

where C is a constant. This implies as well as

as. Since, we have. This implies a contradiction to assumption which had been made. So.

This completes the proof of Lemma. ,

Lemma 2.2. For all, is a Fredholm operator with index zero.

Proof. Indeed, is a Hilbert space, this implies and, we have

It is obviously that is a self-adjoint operator on, we have

, hence

Moreover, fox fixed, the map

is a bounded linear functional in, where . So by the Riesz representation theorem, there is an element in, denote it by, such that

(2.3)

Clearly is linear symmetric and bounded. Moreover T is compact; indeed, let be a bounded sequence in. Passing to a subsequence we may assume that in, in. Use u replaced by and v by in (2.3), and apply Hölder’s inequality with to get

which implies that in. This shows that T is compact. We have

So, where I is an identical operator. By the fact that is a Fredholm operator with index zero, where and T is compact, we obtain that is a Fredholm operator with index zero. This completes the proof of Lemma. ,

Now, we give the abstract perturbation method, which is crucial in our proof of the main results of this paper.

Lemma 2.3. [13] (Abstract Perturbation Method) Let E be a Hilbert space and let be given. Consider the perturbed functional.

Suppose that satisfies:

1) has a finite dimensional manifold of critical points Z, let, for all;

2) for all, is a Fredholm operator with index zero;

3) for all,.

Hereafter we denote by the functional.

Let satisfy (1)-(3) above and suppose that there exists a critical point of such that one of the following conditions hold:

1) is nondegenerated;

2) is a proper local minimum or maximum;

3) is isolated and the local topological degree of at, is different from zero. Then for small enough, the functional has a critical point such that, as.

Remark 2.4. [13] If is compact, then one can still prove that has a critical point near. The set could also consist of local minima and the same for maxima.

3. Proof of the Theorems

We will now solve the bifurcation equation. In order to do this, let us define the reduced functional, see [14] ,

where and verifies as. Hence we are led to study the finite-dimensional functional

The functional can be extended by continuity to by setting

Here we will prove the existence result by showing that problem (1.1) has a positive radial solution provided that h satisfies some integrability conditions. Before giving the proof of the main results, we need the following lemma.

Lemma 3.1. If (H) holds, then as.

Proof. From the definition of and U, we have

where. It is easy to get the first integral in the right hand side; next we show the second integral: In fact,

so we have

we deduce that as.

Proof of Theorem 1. Firstly, we claim that is not identically equal to 0. To prove this claim we will use Fourier analysis. We introduce some notation

that will be used in the following discussion. If, we define

M is nothing but the Mellin transform. The associated convolution is defined by

From the definition, it follows that. Indeed,

With this notation we can write our in the form

We set and

Note that. We have and hence

if, by contradiction, then and one has

On the other hand, is real analytic and so has a discrete number of zeros. By continuity it follows that. Then g and hence h are identically equal to 0. We arrive at a contradiction. This proves the claim. Since, as, and, it follows that has a maximum or a minimum at some. By a straight application of Lemma 2.3 jointly with Remark 2.4, the result follows. ,

Proof of Theorem 2. Using Lemma 3.1, we have as. and can be extended to by continuity setting, where From the assumption, we have

and the condition implies that has a (global) maximum (if) or a (global) minimum (if), at some. This allows us to use the abstract results, yielding a radial solution of problem (1.1), for small. ,

Proof of Theorem 3. It suffices to remark that

If

then (resp.) and, once more has a (global) maximum (resp. a (global) minimum ) at some. ,

In the rest of the section we will give the proof of Theorem 4 and Theorem 5. First we give the following Lemma. Hypothesis (H’) allows us to use the following Riemann-Lebesgue convergence result.

Lemma 3.2 [13] Let be a cube in, and be a T-periodic function. Consider, then

Lemma 3.3 If (H’) holds, then

Proof. Given, there exists large enough such that

On the other hand, the remainder integral over the interval tends to 0 as because of hypothesis (H’) and the Riemann-Lebesgue lemma. ,

Proof of Theorem 4. Using Lemma 3.3, we have as. and can be extended to by continuity setting, where. From the assumption, we have

and the condition implies that has a (global) maximum (if) or a (global) minimum (if), at some. This allows us to use the abstract results, yielding a radial solution of problem (1.1), for small. ,

Proof of Theorem 5. It suffices to repeat the arguments used to prove Theorem 1 using Lemma 3.1 instead of Lemma 3.3.

4. Conclusion

We study a class of semilinear elliptic problems involving critical Hardy-Sobolev exponent and Hardy terms, and obtain positive radial solutions for these problems via an abstract perturbation method in critical point theory. Extensions of nonradial solutions for these problems are being investigated by the author. Results will be submitted for publication in the near future.

Acknowledgements

We would like to thank the editor and the referee for their valuable comments which have led to an improvement of the presentation of this paper.

Fund

This work is supported by Natural Science Foundation of China (No. 11671331); Natural Science Foundation of Fujian Province (No. 2015J01585) and Scientific Research Foundation of Jimei University.

Cite this paper

Lan, Y.-Y. (2017) Positive Radial Solutions for a Class of Semilinear Elliptic Problems Involving Critical Hardy-Sobolev Exponent and Hardy Terms. Journal of Applied Mathematics and Physics, 5, 2205-2217. https://doi.org/10.4236/jamp.2017.511180

References