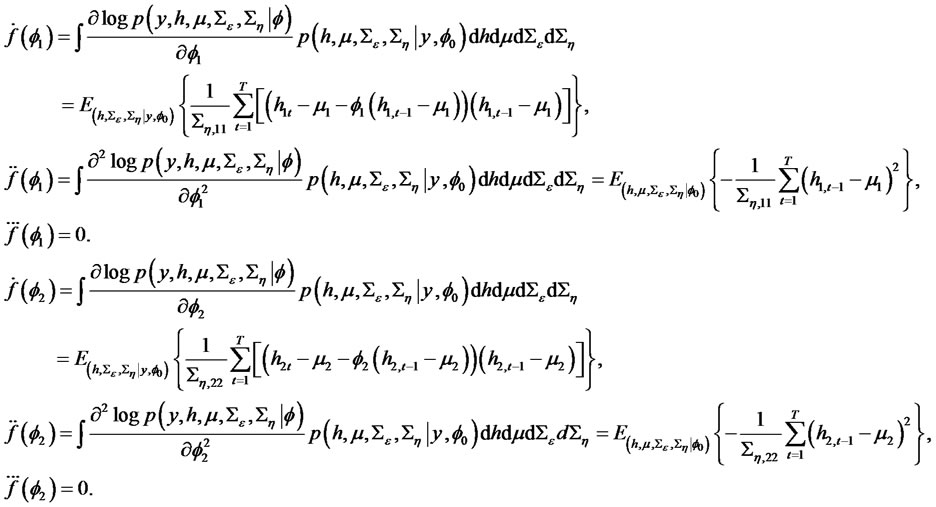Journal of Mathematical Finance
Vol.2 No.1(2012), Article ID:17600,7 pages DOI:10.4236/jmf.2012.21010
Bayesian Testing for Asset Volatility Persistence on Multivariate Stochastic Volatility Models
Sun Yat-sen Business School, Sun Yat-sen University, Guangzhou, China
Email: s04085590@gmail.com
Received September 25, 2011; revised November 25, 2011; accepted November 30, 2011
Keywords: Asset volatility persistency; Bayes factor; Decision theory; Markov Chain Monte Carlo; Unit root testing; Multivariate stochastic volatility models
ABSTRACT
In empirical finance, it is well-known that the volatility of asset returns is highly persistent. The persistence of the volatility process may be checked by testing for a unit root on stochastic volatility models. In this paper, a Bayesian test statistic based on decision theory is developed for testing a unit root on multivariate stochastic volatility models. At last, the developed approach is applied to investigate the persistent effect of financial crisis on the two main stock markets in China.
1. Introduction
It has been well-documented in empirical literature that the volatility of asset returns is highly persistent with time, see Chou [1], Wright [2], Berger, Chaboud and Hjalmarsson [3] and Ewing and Malik [4], etc. If a persistence is observed in the log-volatility process, it means that shocks to volatility do not disappear rapidly and will remain persistent for long periods. Hence, a significant effect will be found in the security price which is caused by some changes in risk premium today. Chou [1] and Bollerslev and Engle [5] studied the volatility of the stock market and its relationship with market fluctuations. They showed that high persistence of shocks to volatility would increase the fluctuation in the volatility which caused the market to plunge. Thus, it is meaningful to develop some efficient methods to check the persistence of the shocks in the volatility process.
In empirical finance, stochastic volatility (SV) models are among the most popular models for modeling timevarying volatility clustering, so that a comprehensive understanding of the types of SV models available, and the potential applications of each, is a useful foundation for research in this field. Shephard [6] provided a review of SV models and applications that was an effective base of reference.
The researchers may check the persistence of shocks in the volatility process by testing for a unit root in stochastic volatility models, see Wright [2]. As to the univariate SV models, So and Li [7] first developed a Bayesian unit root testing approach based on the Bayes factor (Kass and Raftery [8]). Under Bayesian framework, the unit root test problem was regarded as a model comparison problem where two nonnested models, formulated respectively under the null and alternative hypothesis, were compared. Then, the method developed by Chib [9] was used for calculating Bayes factor. However, this method required the marginal likelihood, a marginalization over the unknown parameters and latent volatility under each model. In SV models, the number of unknown parameters and latent volatilities was very large (exceeding the number of observations), hence, obviously, the computational burden of the marginal likely-hood was formidable.
By introducing a weighting function rather than using Chib [9]’s method, Li and Yu [10] derived a novel form for the Bayes factor through considering the special structure of the competing models. No marginalization was needed in their new form, with the result that it was more stable numerically. Further, Li, Ni and Zhang [11] proposed another simple numerical procedure for computing the Bayes factor to detect unit root on the basis of path sampling. This procedure was also free of complex marginalization.
In practice, however, the Bayes factor poses a number of theoretical and practical limitations. Kass and Rafety [8] pointed out that if standard noninformative priors were used, the Bayes factor suffered from Bartlett’s paradox. To the best of our knowledge, the problem has not yet been completely solved. In addition, the computations of the Bayes factor for unit root testing in SV models required either the marginal likelihood or the likelihood ratio, though some effective approaches have been developed. This continued to pose a computational challenge and numerical instability. More recent literature has addressed the point-null hypothesis testing problem, for which Li and Yu [12] has developed a decisional Bayesian hypothesis testing approach to replace the Bayes factor. It was shown that the developed Bayesian test statistic may be implemented under noninformative priors, and was only a log-likelihood ratio as a by-product of Bayesian estimation, hence computationally simple and stable.
As to unit root testing problem in the univariate SV models, Zhang, Li and Zhang [13] showed that the decisional Bayesian approach by Li and Yu [12] can achieve better finite-sample behaviors than Bayes factor. In this paper, we consider the asset return volatility persistence on multivariate SV models, which are a generalized extension of univariate SV models. With the development of economic globalization, and as volatility moves together across different markets, modeling volatility in a multivariate framework where the correlation structures are specified is important in many financial applications, such as international portfolio risk management, and asset allocation. The multivariate stochastic volatility setting is also important for different assets in the same financial market, because of the interwinding economic mechanism. More details of this issue were developed in the review paper about multivariate SV models by Asai, et al. [14]. Also, development of the Bayesian test statistic for testing a unit root is based on the work of Li and Yu [12].
The remainder of this paper is organized as follows. In Section 2, we describe the multivariate stochastic volatility models. The problem of the unit root test is discussed in Section 3. Section 4 considers an empirical application on time series data covering the subprime crisis. This paper is concluded in Section 5.
2. Multivariate Stochastic Volatility Models
The standard Multivariate SV model proposed by Harvery, et al. [15] is given by:
 (1)
(1)
where 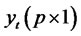 is the return times series,
is the return times series,
 is an p-dimensional unknown log volatility, the operator ◦ denotes the element-element product.
is an p-dimensional unknown log volatility, the operator ◦ denotes the element-element product.  and
and ![]() are both p-dimensional iid normal error for all t. Generally, for
are both p-dimensional iid normal error for all t. Generally, for ,
, 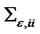 is set as 1.0 and
is set as 1.0 and 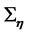 is set as a diagnoal matrix.
is set as a diagnoal matrix.
Because the observable log-likelihood function is involved in intractable high-dimensional integrals, analysis of multivariate SV models is challenging. A variety of estimation methods, including simulated method of moments and simulated maximum likelihood methods, have been proposed for analyzing these models. According to Yu and Meyer [16], the Bayesian method using Markov chain Monte Carlo (MCMC) techniques ranks as one of the most efficient estimation approaches. From this standpoint, we analyze the multivariate SV models of this paper by using MCMC techniques.
Let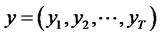 , and
, and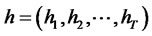 . Under Bayesian framework, the statistical inference is based on the posterior distribution of the parameters given the data, i.e.,
. Under Bayesian framework, the statistical inference is based on the posterior distribution of the parameters given the data, i.e., . However, owing to the complexity induced by latent volatility h, it is almost impossible to evaluate the expectation of this posterior density directly. To alleviate this difficulty in the posterior analysis, we used the data-augmentation strategy (Tanner and Wong [17]) to augment the observed variable y with the latent volatility h. Hence, instead of simulating the observations from
. However, owing to the complexity induced by latent volatility h, it is almost impossible to evaluate the expectation of this posterior density directly. To alleviate this difficulty in the posterior analysis, we used the data-augmentation strategy (Tanner and Wong [17]) to augment the observed variable y with the latent volatility h. Hence, instead of simulating the observations from , we generated some random observations from the joint posterior distributions, i.e.,
, we generated some random observations from the joint posterior distributions, i.e.,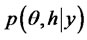 . The simulations can be realized via a MCMC technique named Gibbs-sampler. More concretely, we start with an initial value
. The simulations can be realized via a MCMC technique named Gibbs-sampler. More concretely, we start with an initial value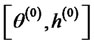 , and then simulates one by one; at the jth iteration, with current values
, and then simulates one by one; at the jth iteration, with current values :
:
1) Initial parameter  and latent volatility h.
and latent volatility h.
2) Generate  from
from .
.
3) Generate 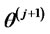 from
from .
.
Observations obtained from the posterior simulation can be used for statistical inference. After the burning-in phase, that is, sufficiently many iterations of this iteration procedure, the simulated random samples can be regarded as efficient random observations from the joint posterior distribution .
.
Let 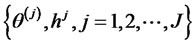 be the simulated efficient random observations. Then, Bayesian estimates of
be the simulated efficient random observations. Then, Bayesian estimates of 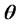 and latent volatility h as well as their standard errors can be easily obtained via the corresponding sampling mean and sample covariance matrix. The concrete forms are given as follows:
and latent volatility h as well as their standard errors can be easily obtained via the corresponding sampling mean and sample covariance matrix. The concrete forms are given as follows:

3. Unit Root Testing under Decision Theory
In this paper, the persistency of volatility is equivalent to testing a root for the autoregressive coefficient 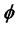 on logvolatility given by:
on logvolatility given by:
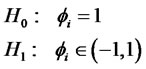 (2)
(2)
As to the problem, it is known that 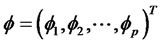 is the interest parameter vector, the other parameters are the nuisance parameters denoted by
is the interest parameter vector, the other parameters are the nuisance parameters denoted by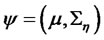 .
.
3.1. Unit Root Testing as a Decision Problem
Generally, the observable data 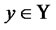 in term of parameter
in term of parameter  and parameter
and parameter  is fitted by some model
is fitted by some model . The model
. The model
 denotes a model which provides a description of the probabilistic behavior of observable data when the null hypothesis H0 is true. According to the work of Li and Yu [12], the unit root testing problem can be regarded as a decision problem where the action space has only two elements, namely to accept (a0) or to reject (a1) model M0 as a convenient proxy for model M.
denotes a model which provides a description of the probabilistic behavior of observable data when the null hypothesis H0 is true. According to the work of Li and Yu [12], the unit root testing problem can be regarded as a decision problem where the action space has only two elements, namely to accept (a0) or to reject (a1) model M0 as a convenient proxy for model M.
With regard to this decision problem, a loss function measuring the loss as a result of accepting or rejecting H0 is required to be specified. Here, we denoted this loss function as . Then, the difference loss function denoted by
. Then, the difference loss function denoted by  can be given as follows:
can be given as follows:
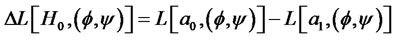
which measures the advantage of rejecting H0 as a function of . Hence, as the optimal decision, rejecting H0 will be made based on the following rule given by
. Hence, as the optimal decision, rejecting H0 will be made based on the following rule given by

3.2. Continuous Loss Function and Bayes Test Statistic
With regard to the hypothesis testing problem, an obvious choice is to use the Kullback-Leibler (KL) divergence function as the difference loss function. However, for multivariate SV models considered in this paper, the likelihood function don’t have closed-form solution so that K-L loss function also don’t have closed-form, hence, can not be applied. Following Li and Yu [12], the continuous divergence function based on 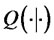 mainly used in EM algorithm is developed to replace K-L divergence function.
mainly used in EM algorithm is developed to replace K-L divergence function.
As to the unit root testing problem, again basing analysis on the work of Li and Yu [12], the continuous loss difference function can be defined as follows:
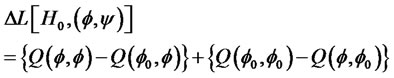
where for any  and
and , the
, the 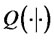 is given by
is given by
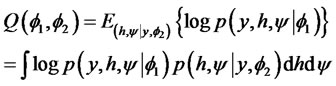
In this situation, the Bayesian test statistic can be expressed as the posterior mean of the loss function, namely,

where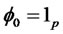 . As shown in Li and Yu [12],
. As shown in Li and Yu [12],  has an equivalent form which is given by
has an equivalent form which is given by
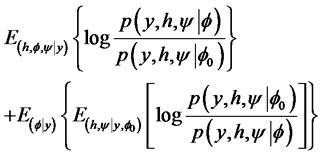 (3)
(3)
This test statistic is composed of two posterior expectations. The first expectation is only a by-product of a Bayesian estimation under alternative hypothesis, and is thus easily approximated using MCMC outputs. The second expectation is difficult to evaluate because it involves two simultaneous expectations, which requires tedious and time-consuming computation. Li and Yu [12] developed a convenient method for approximating this posterior integration. Following their approach for the unit root testing considered here, the details of this numerical approximation are simply summarized as follows:
1) Let ,
,
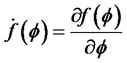 and
and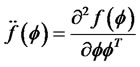 . It is assumed that the regular conditions for the exchange between the integration and differentiation on
. It is assumed that the regular conditions for the exchange between the integration and differentiation on  are satisfied, so we determine that
are satisfied, so we determine that

2) As to the function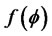 , the second Taylor expansion is taken at (
, the second Taylor expansion is taken at (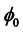 ), so that we find
), so that we find

3) The second posterior integration is given by
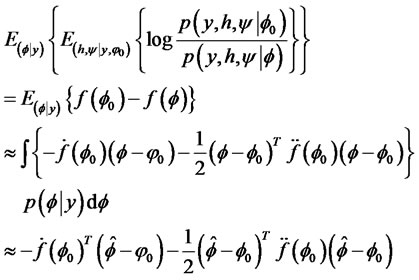
where  is the Bayesian estimation under alternative hypothesis H1.
is the Bayesian estimation under alternative hypothesis H1.
Remark 1: From Equation (3), it can be found that the test statistic is the posterior expectation on the log-likelihood ratio. Compared with the Bayes factor, which is a likelihood ratio, it is more numerically stable on computation.
Remark 2: It can be proved that this test statistic can be implemented under noninformative prior (Li and Yu [12]). Furthermore, the estimation of this test statistic is only the by-product of Bayesian estimation under null and alternative hypothesis; no additional computational efforts are required. This is in sharp contrast to Bayes factor.
Remark 3: In this unit root testing, a threshold value is necessary to be used for deciding whether H0 is rejected or not. Following the approach of Li and Yu [12], the following decision rule is used:
Accept H0 if ; Reject H0 if
; Reject H0 if 
where C is the threshold value. Li and Yu [12] tabulated some threshold values with different probability level. In this paper, we chose the critical value 3.22 as the reference threshold value to express that the unit root hypothesis is rejected or accepted with 99% confidence. More details, one can refer to Li and Yu [12].
4. A Real Study
China stock markets are the emerging stock markets. Since their inception in 1991, they have experienced rapid developments in terms of market size, trading volume, number of listed companies. For shares currently listed in China, the two stock markets—the Shanghai stock market and the Shenzhen stock market, with more than 1500 listings-conduct all trades in Chinese Yuan, The Shanghai market accommodates the largest issuers in terms of market capitalization and, by and large, the Shenzhen caters to smalland medium-sized concerns. In the current stage of Chinese economic development, the capital value of the Chinese stock markets positions them as one of the largest stock markets in the world, surpassed only by the stock market in the United States. Because of its growing importance, foreign investors show significant interests in the Chinese stock markets.
on year 2007, there was a serious financial crisis. In the empirical study, we are mainly concerned whether or not the crisis had a persistent effect in Chinese stock markets because of the economic globalization. The dataset of the Shanghai Composite Index (SHCI) and Shenzhen Composite Index (SZCI) over the period that covers the 2007-2008 subprime crisis was sampled. Daily closing prices for this index was collected from Yahoo.finance for the period of January 4, 2007 to April 22, 2011. The return series has 1046 observations which were plotted in Figure 1. It can be seen that the market was more volatile during the period of the financial crisis.
In the case of this study, we used only the bivariate stochastic volatility models to fit the return series, specifically, p = 2. Regarding the interest parameter , the mixture prior is specified as follows:
, the mixture prior is specified as follows:
 (4)
(4)
here, to investigate the sensitivity of the prior specification, we consider three different prior distributions for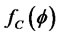 , namely, Uniform(0,1) which is used to represent prior ignorance, two informative prior distributions, Beta (10,1), Beta(20,2). As to the other nuisance parameters, some vague prior distributions are specified as follows:
, namely, Uniform(0,1) which is used to represent prior ignorance, two informative prior distributions, Beta (10,1), Beta(20,2). As to the other nuisance parameters, some vague prior distributions are specified as follows:
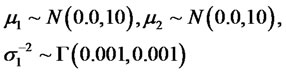 (5)
(5)
Following Yu and Meyer [16], we used the WinBUGS [18] software to draw 50,000 random samples, and discarded the first 30,000 as burn-in samples. The convergence of the Gibbs sampler was diagnosed using the Raftery-Lewis diagnostic test statistic.
In Table 1, the Bayesian estimation and standard error of 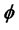 and the value of the Bayes test statistic under three different prior distributions are reported. We can find that the Bayesian estimates of
and the value of the Bayes test statistic under three different prior distributions are reported. We can find that the Bayesian estimates of  are all so very close to unity and doesn’t have significant difference under the different prior specification. As to the estimation of the Bayes test statistic, under different prior specification, some minor difference is observed, and, all values provided the little evidence to reject unit root hypothesis in the volatility of this return series. Not surprisingly, all the results for the unit root test remain nearly the same which show
are all so very close to unity and doesn’t have significant difference under the different prior specification. As to the estimation of the Bayes test statistic, under different prior specification, some minor difference is observed, and, all values provided the little evidence to reject unit root hypothesis in the volatility of this return series. Not surprisingly, all the results for the unit root test remain nearly the same which show

Figure 1. Time series plot for SHCI and SZCI returns over the period from January 4, 2007 to April 22, 2011.

Table 1. Empirical results from SHCI and SZCI index for the period covering the subprime crisis.
that the financial sub-prime crisis happened in 2007-2008 had a long-lasting persistent effect in the main Chinese stock markets.
5. Conclusion and Discussions
Based on the multivariate stochastic volatility models, our paper provides a Bayesian approach to checking persistence of asset return volatility. In sharp contrast to the wellknown Bayes factor, the developed test statistic enjoys at least three advantages: 1) It is well-defined in noninformative prior; 2) Instead of computing the likelihood ratio, it computed the logarithm likelihood ratio, so that the result is generally more stable numerically; 3) It is only a by-product of Bayesian estimation, and does not require more efforts, making its implementation simple. The approach that we developed has been applied to the subprime crisis to check volatility persistence in the SHCI and SZCI index return series. The empirical study confirmed that the financial crisis that happened in 2007 had some long-lasting effects in the Chinese stock markets. Noting that our test was based on the basic multivariate SV models proposed by Harvey, et al. [15], we suggest that our technique is, itself, quite general, and can be applied in many alternative multivariate SV models (for example, factor SV models). Other possible models are discussed in Asai, et al. [14].
6. Acknowledgements
Li gratefully acknowledges the financial support of the Chinese Natural Science fund (No.70901077), the Chinese Education Ministry Social Science fund (No.09YJC 790266), the Fundamental Research Funds for the Central Universities.
REFERENCES
- R. Y. Chou, “Volatility Persistence and Stock Valuation: Some Empirical Evidence Using GARCH,” Journal of Applied Econometrics, Vol. 3, No. 4, 1988, pp. 279-294. doi:10.1002/jae.3950030404
- J. Wright, “Testing a Unit Root in the Volatility of Asset Returns,” Journal of Applied Econometrics, Vol. 14, No. 3, 1999, pp. 309-318. doi:10.1002/(SICI)1099-1255(199905/06)14:3<309::AID-JAE531>3.0.CO;2-X
- D. Berger, A. Chaboud and E. Hjalmarsson, “What Drives Volatility Persistence in the Foreign Exchange Market,” Journal of Financial Economics, Vol. 94, No. 2, 2009, pp. 192-213. doi:10.1016/j.jfineco.2008.10.006
- B. T. Ewing and F. Malik, “Estimating Volatility Persistence in Oil Prices under Structural Breaks,” The Financial Review, Vol. 45, No. 4, 2010, pp. 1011-1023. doi:10.1111/j.1540-6288.2010.00283.x
- T. Bollerslev and R. F. Engle, “Common Persistence in Conditional Variance,” Econometrica, Vol. 61, No. 1, 1993, pp. 167-186. doi:10.2307/2951782
- N. Shephard, “Stochastic Volatility: Selected Reading,” Oxford University Press, Oxford, 2005.
- M. K. P. So and W. K. Li, “Bayesian Unit-Root Testing in Stochastic Volatility Models,” Journal of Business and Economic Statistics, Vol. 17, No. 4, 1999, pp. 491-496. doi:10.2307/1392407
- R. E. Kass and A. E. Raftery, “Bayes Factor,” Journal of the Americana Statistical Association, Vol. 90, No. 430, 1995, pp. 773-795. doi:10.2307/2291091
- S. Chib, “Marginal Likelihood from the Gibbs Output,” Journal of the American Statistical Association, Vol. 90, No. 432, 1995, pp. 1313-1321. doi:10.2307/2291521
- Y. Li and J. Yu, “A New Bayesian Unit Root Test in Stochastic Volatility Models,” Research Collection School of Economics, Paper 1240, 2010.
- Y. Li, Z. X. Ni and J. Zhang, “An Efficient Stochastic Simulation Algorithm for Bayesian Unit Root Testing in Stochastic Volatility Models,” Computational Economics, Vol. 37, No. 3, 2011, pp. 237-248. doi:10.1007/s10614-011-9252-4
- Y. Li and J. Yu, “Bayesian Hypothesis Testing in Latent Variable Models,” Journal of Econometrics, Vol. 166, No. 2, 2012, pp. 237-246. doi:10.1016/j.jeconom.2011.09.040
- J. Zhang, Y. Li and J. Zhang, “Bayesian Testing a Unit Root in the Volatility of Asset Returns: An Empirical Comparison,” Working Paper, 2011.
- M. Asai, M. AcAleer and J. Yu, “Multivariate Stochastic Volatility Models: A Review,” Econometric Review, Vol. 25, No. 2-3, 2006, pp. 145-175. doi:10.1080/07474930600713564
- A. C. Harvey, E. Ruiz and E. Shephard, “Multivariate Stochastic Variance Models,” Review of Economic Studies, Vol. 61, No. 2, 1994, pp. 247-264. doi:10.2307/2297980
- J. Yu and R. Meyer, “Multivariate Stochastic Volatility Models: Bayesian Estimation and Model Comparison,” Econometric Review, Vol. 25, No. 2-3, 2006, pp. 361-384. doi:10.1080/07474930600713465
- T. A. Tanner and W. H. Wong, “The Calculation of Posterior Distributions by Data Augmentation,” Journal of the American Statistical Association, Vol. 82, No. 398, 1987, pp. 528-549. doi:10.2307/2289457
- D. J. Spiegelhalter, A. Thomas, N. G. Best and D. Lunn, “WinBUGS User Manual. Version 1.4,” MRC Biostatistics Unit, Cambridge, 2003.
Appendix: Calculation of  for Multivariate Stochastic Volatility Model
for Multivariate Stochastic Volatility Model
As to the multivariate stochastic volatility model considered in this paper, the joint density function for the observable data and latent volatility is given by:
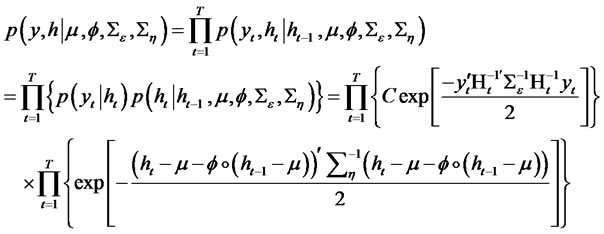
where C is a known constant. The observable likelihood function can be expressed as:

Here, it can be seen that owing to the latent volatility, the observable likelihood function is a high-dimensional multiple integral which does not the closed-from expression.
According to Section 3, to approximate the Bayesian test statistic, 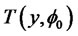 , several components are derived as follows:
, several components are derived as follows:

As to the bivariate multivariate SV model in this empirical study, we may derive the concrete form given by:

Moreover,