Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27388,4 pages DOI:10.4236/ojdm.2013.31010
A Note on a Combinatorial Conjecture
School of Mathematical Science, Guangxi Teachers Education University, Nanning, China
Email: dengguixin@live.com
Received October 7, 2012; revised November 7, 2012; accepted November 17, 2012
Keywords: Binary String; Weight
ABSTRACT
It is difficult to find Boolean functions achieving many good cryptographic properties. Recently, Tu and Deng obtained two classes of Boolean functions with good properties based on a combinatorial conjecture about binary strings. In this paper, using different approaches, we prove this conjecture is true in some cases. This conjecture has resisted different attempts of proof since it is hard to find a recursive method. In this paper we give a recursive formula in a special case.
1. Introduction
Let x be a nonnegative integer. If the binary expansion of x is
 then the Hamming weight of x is
then the Hamming weight of x is
 .
.
In [1] Tu and Deng proposed the following conjecture.
Conjecture 1: Let

where . Then the cardinality
. Then the cardinality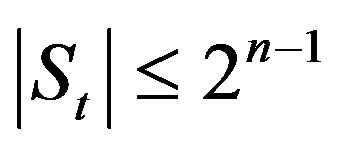 .
.
Based on this conjecture, Tu and Deng [1] constructed two classes of Boolean functions with many good cryptographic properties. In this paper we always use the following bijection, where  is the set of binary strings of length
is the set of binary strings of length  except the string consisting of n copies of 1.
except the string consisting of n copies of 1.
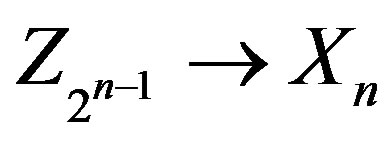

We use  to denote the length of a binary string
to denote the length of a binary string
 . Let
. Let . And we use the following notation
. And we use the following notation  where there are k consecutive 1 and m consecutive 0 in the string.
where there are k consecutive 1 and m consecutive 0 in the string.
In [1] Tu and Deng construct an algorithm which they used it to show that the conjecture above is true when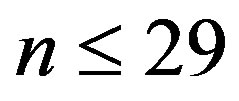 . Cusick, Li and Stanica [2] show that Conjecture 1 is true when
. Cusick, Li and Stanica [2] show that Conjecture 1 is true when . In this paper, we will consider the following conjecture, which is equivalent to Conjecture 1.
. In this paper, we will consider the following conjecture, which is equivalent to Conjecture 1.
Conjecture 2: Suppose that 
Let

then .
.
The following lemma is easy so we omit the proof.
Lemma 1.1 Let  Then following statements are true:
Then following statements are true:
1) 
2) ;
;
3) The map  is bijective.
is bijective.
Hence 
So the authors in [3] actually showed that Conjecture 2 is true when
 .
.
According to Lemma 1.1. Deng and Yuan [4] show that Conjecture 2 is true if 
The outline of this paper is as follows. In Section 2 we introduce some notations. In Section 3, we consider what happen if we change some digit 1 into 0 in the strings. We get a recursive formula about  and prove a new case of the conjecture.
and prove a new case of the conjecture.
2. A Partition of 
The following lemma is about the relation between  and
and , which is proved in [4].
, which is proved in [4].
Lemma 2.1 Let


Suppose that
 where
where  Assume that
Assume that . Then
. Then

where we set 
Let

for any  and
and 
Then
 and
and 
which are disjoin unions. We define a partition on  according to Lemma 2.1.
according to Lemma 2.1.
Definition 2.1 Let  be a binary string of length n. Suppose that
be a binary string of length n. Suppose that
 and
and 
where  Let
Let  be a binary string. Suppose that
be a binary string. Suppose that
 where
where  We set
We set 
to be the subset of  such that
such that 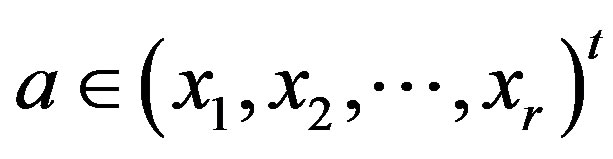 if and only if the following two conditions hold i)
if and only if the following two conditions hold i) , if
, if 
ii) , if
, if 
And we will use that notation  if
if .
.
Definition 2.2 Let 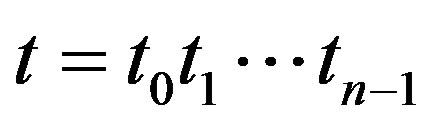 and
and  be two given binary strings. For any
be two given binary strings. For any , we set
, we set , if
, if  for each
for each .
.
We say that  is free if there are two strings
is free if there are two strings  and
and  in
in  such that
such that  and
and .
.
From Definition 2.1 and Lemma 2.1 we see that
 and
and where k is the number of indices such that
where k is the number of indices such that  is free.
is free.
Example 2.1 Let
 ,
,  ,
,  and
and

Then
 and
and
 ,
,
 ,
,
 .
.
So
 ,
,  and
and .
.
Moreover, by Definition 2.2  if and only if
if and only if ,
,  or
or . That is,
. That is,  is free for
is free for . We also have
. We also have  if and only if
if and only if
 ,
, 
if and only if
 ,
,  or
or .
.
3. Main Results
If  with each
with each , then we say that the block of
, then we say that the block of  is
is . Jean-P. Flori and H. Randriam [5] give some asymptotic results when each
. Jean-P. Flori and H. Randriam [5] give some asymptotic results when each . In particular, they show that Conjecture 2 is true if the block of t is smaller than 3 or each
. In particular, they show that Conjecture 2 is true if the block of t is smaller than 3 or each  is sufficient large for a fixed length of block. We give a recursive formula to show that we can restrict our attention to the case each
is sufficient large for a fixed length of block. We give a recursive formula to show that we can restrict our attention to the case each 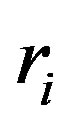 is smaller than the block of
is smaller than the block of 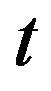 in this situation. They also conjectured that
in this situation. They also conjectured that
 if
if .
.
Lemma 3.1 Let

and

with
 and
and .
.
Let
 for
for ,
,

and

Then

Proof. Note that for any , if
, if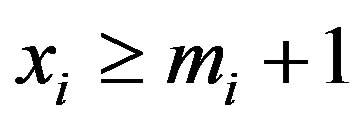 , then
, then  for each
for each , moreover in this case we have
, moreover in this case we have
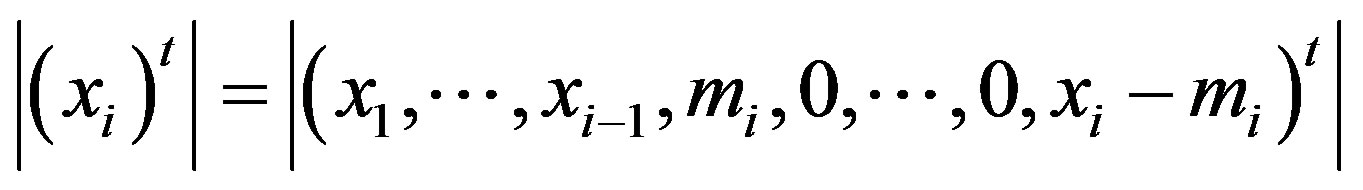 .
.
Let


then . Similarly we write
. Similarly we write
 where
where


We observe that if , then
, then  if and only if each
if and only if each  Now if
Now if  by comparing the number of free indices we have
by comparing the number of free indices we have
 .
.
Hence,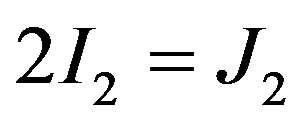 . If each
. If each , then
, then
 .
.
Suppose that . Then
. Then

So

Therefore


This finishes the proof.
Remark 3.1 Let  with
with . It is clear that
. It is clear that

for any  So we use the following notation
So we use the following notation  means that there are sufficient consecutive 0 in the string.
means that there are sufficient consecutive 0 in the string.
We set

for .
.
Theorem 3.1 Let
 ,
,  ,
,
 ,
,  ,
,
 ,
,  where each
where each  and
and  Then
Then
 .
.
Proof. Suppose that those strings have the same length and . By Lemma 3.1
. By Lemma 3.1



Let
 .
.
If , by comparing the number of free indices we have
, by comparing the number of free indices we have
 where
where . We set
. We set

and
 .
.
Then

Let
 and
and
 .
.
Now consider the following mapping  and
and . If
. If
 and
and then
then
 .
.
Then
 .
.
So
 .
.
If
 then
then
 .
.
It is easy to see that
 and
and .
.
By the discussion above we obtain
 , and
, and .
.
This finishes the proof.
Corollary 3.1 With the same notations in Theorem 3.1. Suppose that
 then
then
 .
.
Proof. We proof the statement by induction on
 .
.
The case  implies that
implies that
 .
.
This was proved in [4]. Without loss of generality we can assume that  and
and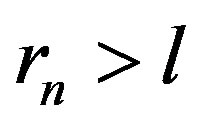 . By induction
. By induction
 by Theorem 3.1
by Theorem 3.1
 .
.
The proof is completed by induction on .
.
Corollary 3.2 Let . Then
. Then
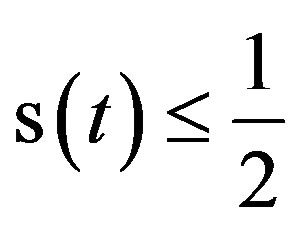 .
.
Proof. By Corollary 3.1 it suffice to show that case when each . So we have
. So we have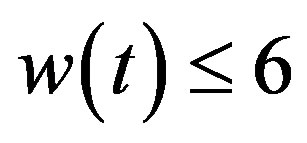 , which is proved in [4].
, which is proved in [4].
REFERENCES
- Z. Tu and Y. Deng, “A Conjecture on Binary String and Its Application on Constructing Boolean Functions of Optimal Algebraic Immunity,” Designs, Codes and Cryptography, Vol. 60, No. 1, 2010, pp. 1-14. doi:10.1007/s10623-010-9413-9
- G. Cohen and J.-P. Flori, “On a Generalized Combinatorial Conjecture Involving Addition Mod
 ,” IACR Cryptology ePrint Archive, Vol. 400, 2011, in press.
,” IACR Cryptology ePrint Archive, Vol. 400, 2011, in press. - T. W. Cusick, Y. Li and P. Stanica, “On a Combinatorial Conjecture,” Integers, Vol. 11, No. 2, 2011, pp. 185-203. doi:10.1515/integ.2011.017
- G. Deng and P. Yuan, “On a Combinatorial Conjecture of Tu and Deng,” Integers, Vol. 12, No. A48, 2012.
- J.-P. Flori and H. Randriam, “On the Number of Carries Occuring in an Addition Mod
 ,” Integers, Vol. 12, No. A10, 2012.
,” Integers, Vol. 12, No. A10, 2012.

