Received 23 August 2015; accepted 17 September 2015; published 21 September 2015

ABSTRACT

Basic assumptions are proposed for the continuity model of a tubular hollow slab combined with continuity analysis and calculation of a finite-element model; the continuity Equation of a tubular hollow slab at the minor axis supported at two ends of the hollow axle under a vertical even load is determined and solved. The overall equivalent flexural rigidity is then determined, which provides important conditions for the continuity analysis of tubular hollow floor supported along four sides.

Keywords:

Continuity Analysis, Hollow Slab, Equivalent Flexural Rigidity, Deflection, Finite-Element Analysis

1. Introduction

In China, there are three main calculation methods used in the design of cast-in-situ concrete hollow floors, i.e., basic flexure theory method, one-way slab method, and finite-element method. 1) Basic flexure theory method has been widely used in industry but requires relatively large error tolerance. In early engineering practices the hollow slab and the solid slab were assumed with same structural performance. Hence when analyzing the stress and deflection, the hollow slab can be directly converted into the solid slab without considering the local bending caused by punching. Obviously, the assumption may cause tremendous error or even wrong results, and is unacceptable in current specifications. 2) One-way slab method is conveniently used for the calculation of internal forces. The slab can be one pitch (or several pitches) in width. Therefore, the internal force can be determined with the simply supported beam in single span or continuous beam with many supports. In this method, the reinforcement can be simplified as the I-shaped section by equal area, centroid, and equal moment of inertia, which can be calculated by the determined internal force. This method only considers the rigidity in one direction, easy to form crack at the minor axis. Although it is superior to the first method, it actually goes against the bidirectional loading. 3) Finite-element method (FEM) is most generally used for structural analysis including the tubular slab analysis. Although it provides accurate results, it is not commonly used because the modeling process is time consuming and requires a lot of computational efforts. Additionally, nonlinear performance of the hollow slabs is hard to express using FEM due to difficulties in convergence.

The equivalent rigidity method has been used for the convenience of calculation due to the complex structure system of hollow slabs, with large or small holes. In fact, the equivalent rigidity indirectly reflects the rigidity by the structure deformation, i.e., under the same load, the smaller the displacement, the larger the rigidity. In terms of the equivalent flexural rigidity (EI)_0H of the hollow slab: if the midspan deformation of the upper slab or the lower slab under the vertical even load for hollow slab structures at minor axis is equal to that under the same vertical load for the overall tubular hollow slab at minor axis, it is considered that the rigidity of the structures is equivalent to that of the overall.

2. Differential Equations of Tubular Hollow Slab

2.1. Assumptions of Tubular Hollow Slab

The section in the direction of the hollow axis can be regarded as the I-shaped girders with the upper and lower flanges connected, namely the major axis. Therefore, the section rigidity is quite large and can be calculated easily. Figure 1 shows the continuity model for the actual structure of hollow slab. In Figure 2, YZ denotes the major axis while XZ the minor axis. The section perpendicular to the hollow axis can be regarded as the “=” shaped section at the thinnest upper and lower flanges, namely the minor axis, of which the rigidity is smaller than that in the direction of the hollow axis. This paper addresses the tubular hollow slab at the minor axis, which is supported at the two ends parallel to the hollow axis. Certain reasonable and necessary assumptions are introduced as follows:

1) The top and bottom of the core tube of the cast-in-situ hollow slab are considered as the upper and lower layers of the continuum, with the arris of slab as the sandwich layer where the effects of bending and shearing are determined. In this way, the structures only connected by the arris of upper and lower slabs become the continuous structure connected by the continuous connecting rods in the whole span, and the connection by the finite points becomes that by the infinite points, with the bending, shearing, and axial force considered.

2) The arris between the upper and lower slabs are regarded as the sandwich of the continuum, which is the continuous sandwich mainly bearing the shear if distributed evenly over the entire beam and passes the axial stress if considering the effects of deformation caused by bending and shearing. In addition, the upper and lower slabs share the same vertical displacements without considering the axial deformation.

3) It is assumed that the upper and lower slabs share the same angle and curvature at X, and the inflection point of the sandwich is just the midpoint under the transverse load.

4) In structural design, no structural damage would occur, so the material is assumed to perform within linear elastic range.

According to the Assumption (3) the inflection point of the sandwich is just the midpoint under the transverse load, and the bending moment is zero at the midpoint, as shown in Figure 3 (calculation diagram for continuity of hollow slabs). It is assumed that the sandwich with holes at the hollow is distributed evenly on the whole beam and cut apart along its midpoint, with τ_(x) denoting the shearing force and σ_(x) denoting the axial force. The σ_(x) has nothing to do with the solution, therefore, there is no need to solve it. The continuity conditions for the deformation along the τ_(x) can be expressed as Equation 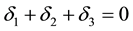(1).

(1)

where δ₁ denotes the relative displacement of upper and lower slabs caused by the bending deflection, as shown in Figure 4(a); δ₂ denotes the relative displacement of upper and lower slabs caused by the axial deformation, as shown in Figure 4(b); δ₃ denotes the relative displacement of continuity sandwich caused by the bending deflection and axial deformation, as shown in Figure 4(c); and the superposition of δ₁, δ₂, and δ₃ is the total displacement δ along the τ_(x) of the basic system under the outer load, axial force of notch, and shearing force τ_(x), which can be expressed as Equation 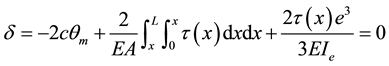(2).

(2)

where 2c denotes the distance between centroid of the upper and lower slabs; A denotes the cross-sectional area in the unit width of the upper and lower slabs; L denotes the beam length; I_e = Ĩ_b/b denotes the equivalent moment of inertia per unit length of the continuity, namely the average moment of inertia per unit length of the sandwich, with b denoting the distance between two holes; and 2e denotes the clear distance between two slabs.

2.2. Solutions for the Differential Equation

By re-organizing Equation (2), we can get Equation 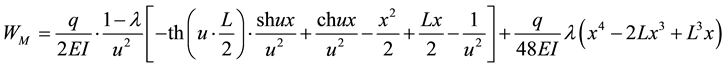(3).

(3)

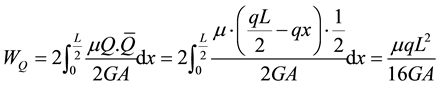
where W_Q denotes the shear deformation of upper and lower slabs caused by the shearing force Q, with μ denoting the coefficient of cross-section shape, 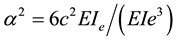, ,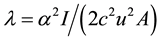; EI denotes the flexural rigidity of upper or the lower slabs against the center; q denotes the evenly-distributed load; and G denotes the shear modulus. Since the shear deformation (W_Q) is not usually considered when the section height is far less than the span [1] , the total deflection of the slab satisfies the following Equation: W = W_M.

The average moment of inertia per unit length of the sandwich (I_e) is required for the solution of α. Use the upper part for analysis of one unit between holes, as shown in Figure 5. If the a-a section is under the unit force, the center web plate can be considered as the cantilever that causes deformation, where the effects of shear deformation are as Equation 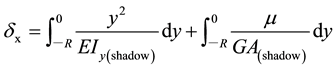(4).

(4)

It is assumed that the sandwich section is rectangular, but it is in the shape of shadow in practice. The principle for the average moment of inertia per unit length is that the deformation caused by the same shear is equal.

In order to solve I_e, the ANSYS finite-element software and PLANE42 computing element is used (with the plane-strain element selected) to calculate the displacement of the hollow slab in the commonly used specifications in Figure 5 and thus the equivalent moment of inertia of sandwich (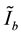). The Equation 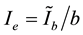is used to solve I_e (b = 2R + d, denoting the spacing between adjacent holes. Figure 6 shows the relationship between I_e, d (clear distance between holes), and 2R (hole diameter).

3. Numerical Simulation

In order to verify the derived Equation and according solutions, finite-element analysis is performed for the horizontal stress in the x direction of the tubular hollow slab. The stress distribution under the bending shear and simple bending is calculated with the commercial software ANSYS.

3.1. Finite Element Model

Element SOLID45 (the non-coordinated 8-node 3D entity element BRICK) is used for all the structure components

within the linear and elastic range. In the Equation, the denominator denotes the moments of inertia of the cross-section of upper and lower slabs against the centroid axis of the combined section, namely the centroid axis of hollow slab (x-axis). Equation (3) does not consider the influence of the sandwich between the holes. Considering the effect of the sandwich (namely the ribbed part between slabs), the denominator is assumed as the moments of inertia (I_c0) of the effective cross-section (the shaded area in Figure 7) against the centroid axis of the hollow slab (x-axis). The section stress of the tubular hollow axis at the minor axis is analyzed first in order to solve λ [2] .

When calculating the deflection and bending moment at the minor axis with the effect of sandwich part

considered, it shall set out from the section stress at the minor stress whether consider the effect of the whole section and its degree. When we calculate the vertical deflection and bending moment of one section at the minor axis, it is necessary to analyze the horizontal stress in the x direction for the beam supported at the major axis.

It can be seen from the analysis that the stress is distributed unevenly. If the edge stress is 1 for the top of the upper slab and the bottom of the lower slab, the edge stress of the hole will be smaller than 1 and the inner stress will be greater than 1, therefore, there is a stress concentration phenomenon. There is a zero stress line at the half height of the sandwich, where the stress is close to zero. There is even opposite sign of stress at the center of arris within the zero stress line under the bending and shearing, which is also applicable to the section stress at the minor axis of the tubular hollow slab.

The stress at the center of arris is zero, indicating that it makes no contribution to the overall rigidity, and it can be neglected when calculating the overall equivalent rigidity. The uneven distribution of stress can also be neglected when calculating the overall equivalent rigidity. The equivalent rigidity in the x direction of the tubular hollow slab can be calculated by the effective height of the cross-section.

When calculating the overall equivalent rigidity, the uneven distribution of stress can be neglected, and the zero stress line can be considered as horizontal and straight. It is assumed that the vertical angle is θ for the hole radius corresponding to the zero stress line. Take the section within a unit length (b) to solve the moment of inertia at the centroid axis for the shaded area of the effective section against the combined section. Take the length parallel to hollow axis as a.

The moment of inertia at the centroid axis for the t₁ shaded area of the upper and lower slabs against the com-

bined section:, where;

the moment of inertia at the centroid axis for the t shaded area of the upper and lower slabs against the combined

section:. The moment of inertia at the centroid axis for the shaded area of the effective

section against the combined section is I_c.

The moment of inertia at the centroid axis (X axis) of the combined section for the whole hollow slab in unit length is I_c0.

(5)

A finite-element subdivision model is used to analyze the bending shear and the simple bending in the x direction for the tubular hollow slab for the commonly used specifications. The unknown parameter θ in the Equationis solved with the numerical method by the analysis results, which is basically the same. In the principle of appropriate merger for the sake of employment, take θ = 22.5˚ for the tubular hollow slab frequently used in engineering.

After considering the effect of sandwich, we get

(6)

3.2. Numerical Results

The deflection of the tubular hollow slab supported at two ends along the slab can be used to solve the maximum deflection at the span midpoint of the hollow slab, and thus the overall equivalent flexural rigidity, by the theory of continuity.

In terms of the deflection of the tubular hollow slab supported at two ends along the slab, it can be seen from Equation (3) that

(7)

where, , of which I_e is as shown in Figure 6 and λ can be

solved with Equation (6).

For instance: As shown in the practical structure of the hollow slab in Figure 1, the tubular hole of the hollow slab satisfies 2R = 0.15 m and d = 0.05 m, with the hole located in the center. C30 concrete is used, with Poisson’s ratio (u) of 0.2 and Ec = 3 × 10¹⁰ N/m². Take 1m along the direction of the hole from the whole span (7 m). It is required to solve the deflection of various points on the tubular hollow slab at the minor axis when the area load is 4 kN/m² and supported at the major axis.

In Equation (7) solved using the continuity method, α² = 1939, u² = 989.6, and λ = 0.019489. Another method is to use the SOLID45 entity unit of ANSYS, taking 0.0125 m × 0.0125 m in the XY section and 0.0125 m × 0.25 m in the YZ section for the mesh generation. Table 1 gives the deflection of each point. It can be seen from the table that the ratio of deflection solved with the two methods is 1.01, indicting it is right to analyze the tubular hollow slab in the horizontal using the continuity method.

3.3. Comparisons and Verifications

In terms of the equivalent flexural rigidity (EI)_0H of the hollow slab: if the midspan displacement of the upper slab or the lower slab under the vertical even load for hollow-slab structures in the minor axis is equal to that under the same vertical load for the equivalent solid slab, it is considered that the rigidity of the structures are equivalent to that of the overall. The (EI)_0H can be solved as Equation (8):

(8)

where ξ₁ = 0.35514, cos³θ = 0.78878, sinθ = 0.38268, and EI denotes flexural rigidity of the upper slab or the lower slab.

It can be seen from Equation (8) that the reduction coefficient of the overall equivalent flexural rigidity in the

Note: x indicates the distance between the computing point and the centre of the left support.

minor axis of the slab is mainly related to c/t, 2R/t, and 2R/b, and increases with c/t and 2R/t, proportionate to the square of c/t and the cube of 2R/t. It is mainly affected by c/t but less affected by 2R/b.

The deduction above about the overall flexural rigidity is also applicable to the holes of non-circular tubes, but the effective cross-section is that of the non-circular tubes. In terms of the tubular hollow-slab types of commonly-used specifications, the overall equivalent flexural rigidity (EI)_0H in the horizontal of the hollow slab can be calculated by Equation (8) with different c/t, 2R/t, and 2R/b.

4. Conclusion

The continuity method is proposed to calculate the equivalent rigidity at the minor axis of concrete hollow slab. After derivations of the differential Equations, we can derive vertical deflection of the fundamental Equation and the overall equivalent flexural rigidity for the tubular hollow slab in the minor axis supported at two ends in the major axis. Through a numerical example, the deflection Equation is verified to be accurate and efficient. It is practical to get the equivalent flexural rigidity in the major axis, therefore, the continuous analysis is readily solved for the tubular hollow floor supported along four sides.

Cite this paper

RonglanZhang, (2015) Equivalent Rigidity at the Minor Axis of Concrete Hollow Slab Based on Continuity Analysis. Engineering,07,545-552. doi: 10.4236/eng.2015.79050

References