Applied Mathematics
Vol.5 No.10(2014), Article
ID:46190,7
pages
DOI:10.4236/am.2014.510131
A Global Stability Analysis of a Susceptible-Infected-Removed-PreventedControlled Epidemic Model
Muhammad A. Yau, Hussaini S. Ndakwo, A. M. Umar
Department of Mathematical Sciences, Nasarawa State University, Keffi, Nigeria
Email: Yau4real2006@yahoo.com, hsndakwo@yahoo.com, abdulmallam@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 15 March 2014; revised 15 April 2014; accepted 22 April 2014
ABSTRACT
A mathematical model of HIV transmission dynamics is proposed and analysed. The population is partitioned into five compartments of susceptible S(t), Infected I(t), Removed R(t), Prevented U(t) and the Controlled W(t). Each of the compartments comprises of cohort of individuals. Five systems of nonlinear equations are derived to represent each of the compartments. The general stability of the disease free equilibrium (DFE) and the endemic equilibrium states of the linearized model are established using the linear stability analysis (Routh-Hurwitz) method which is found to be locally asymptotically stable when the infected individuals receive ART and use the condom. The reproduction number is also derived using the idea of Diekmann and is found to be strictly less than one. This means that the epidemic will die out.
Keywords:Epidemic Model, Stability Analysis, HIV/AIDS, Disease Free Equilibrium Points

1. Introduction
One of the greatest threats to human survival in contemporary times is the Human Immune deficiency Virus (HIV) pandemic. The Human Immune deficiency Virus is understood to be the causative agent of the deadly disease called the Acquired Immune Deficiency Syndrome (AIDS), Centers for Disease Control and Prevention, (1989) [1] . The virus destroys antibodies and weakens the defense or immune system of the body, to the extent that the infected person becomes vulnerable to all forms of diseases, Tinuola, (2006) [2] . Presently there is no known medical cure for the disease therefore; all programmes on HIV are geared towards preventing the spread of the epidemic rather than curing the disease. Although there are no drugs for the cure of the disease presently, but there is an Antiretroviral Therapy/Drug (ART) that is available which prolongs the life span of the infected people. ART is a special programme design to counsel and care for people living with HIV. ART does not cure HIV infection; it only boosts the immune system of infected people against secondary infections, thereby prolonging their life span Kimbir et al., (2008) [3] . Another method of control includes the use of barrier contraceptives. A major method, apart from the use of the condom, in the control of HIV, is Antiretroviral Therapy (ART). By this approach, HIV positives are detected and placed on Antiretroviral Drugs (ARD). Generally, there are public awareness campaigns which are intended to educate the public on the spread of HIV and how to control it Kimbir et al., (2008) [3] and Muhammad, (2010) [4] . Members of the public are encouraged to go for test in order to determine their HIV status so as to benefit from ART. When the epidemic started, the major victims were highly educated people. Nowadays, more than 60% of the infected population has not yet finished elementary school according to the official data available in the site Yang et al., (1999) [5] . In this social group, the number of people who have access to information about AIDS is insignificant. Even some basic information such as transmission mechanisms or prevention methods is too far from their reality. They are neither subjected to periodic tests of HIV-prevalence nor do they have a positive prevention attitude. Besides, the low standards of public health services contribute to worsening of the situation.
The main aim of this research is to propose a modified mathematical model of HIV transmission dynamics that will be used to check for the spread of the epidemic and to check for the effectiveness of Antiretroviral Therapy (ART) and the use of a preventive measure (condom) is in controlling the spread of HIV/AIDS. In general, these are some of the objectives of the research:
Ÿ To investigate the extent to which, Antiretroviral Therapy and the use of a preventive measure (condom) will reduce the spread of the virus;
Ÿ To provide information to guide advocacy and future program planning;
Ÿ Institutionalizing best practices in care and support for people living with HIV/AIDS;
Ÿ And to stimulate more researches on HIV/AIDS.
2. Methodology
To derive the modified model and to establish the general stability of the free equilibrium states of the model, three methods would be used. First we would use the method of Kimbir et al., (2008) [3] to do linear stability analysis, secondly, we would consider the Routh-Hurwitz stability condition as in Hethcote, (1989) [6] and finally we would use the method of Diekmann et al., (1990) [7] .
3. The Model
We partition the population into five compartments of Susceptible S(t), Infected I(t), Removed R(t), Prevented U(t) and the Controlled W(t). Asusceptible is an individual that is yet to be infected, but is open to infection as he or she interacts with members of the I-class. An infected individual is one who has HIV and is at some stage of infection. A received individual is one that is confirmed to be HIV positive, counselled, and is receiving Antiretroviral Therapy. A prevented individual is one who is confirmed to be HIV positive, counselled, and is using a preventive measure. A controlled individual is one that is confirmed HIV positive, counselled, and is both receiving ART & using condom. Eventually, we will establish the stability of the equilibrium states of the model. See table 3.1 for details of the definition of the model parameters.
3.1. Model Parameters
 The number of susceptible individuals at time t,
The number of susceptible individuals at time t,
 The number of infected individuals at time t,
The number of infected individuals at time t,
 The number of infected individuals receiving ART at time t,
The number of infected individuals receiving ART at time t,
 The number of infected individuals using condom at time t,
The number of infected individuals using condom at time t,
 The number of infected individuals receiving antiretroviral therapy and using condom at time t,
The number of infected individuals receiving antiretroviral therapy and using condom at time t,
 Natural birth rate,
Natural birth rate,
 Natural death rate,
Natural death rate,
 Death rate due to infection in class I,
Death rate due to infection in class I,
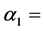 Death rate due to infection in class R,
Death rate due to infection in class R,
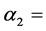 Death rate due to infection in class U,
Death rate due to infection in class U,
 Probability of transmission by members in class-I,
Probability of transmission by members in class-I,
 Probability of transmission by members in class-R,
Probability of transmission by members in class-R,
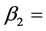 Probability of transmission by members in U-class,
Probability of transmission by members in U-class,
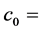 Average number of sexual partner of members of class I,
Average number of sexual partner of members of class I,
 Average number of sexual partner of member of class R,
Average number of sexual partner of member of class R,
 Average number of sexual partner of member of U-class
Average number of sexual partner of member of U-class
![]() Average number of sexual partner of member of W-class
Average number of sexual partner of member of W-class
 The proportion of infected individuals that received ART at time t,
The proportion of infected individuals that received ART at time t,
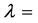 The proportion of infected individuals that used the condom at time t,
The proportion of infected individuals that used the condom at time t,
 The proportion of infected individuals that received ART first and later used the condom at time t,
The proportion of infected individuals that received ART first and later used the condom at time t,
 The proportion of infected individuals that used the condom first and later received ART at time t,
The proportion of infected individuals that used the condom first and later received ART at time t,
 Maximum lifespan after infection for members of W-class.
Maximum lifespan after infection for members of W-class.
3.2. The Model Equations
From the model assumptions, assuming that the birth rate b is proportional to the total population N, there is a natural death rate µ in all compartments, and there are disease-induced death rates in the (I, R, U, W) sub-classes denoted by α0, α1, α2, α respectively. We obtain the following model equations;
 (3.11)
(3.11)
 (3.12)
(3.12)
 (3.13)
(3.13)
 (3.14)
(3.14)
 (3.15)
(3.15)
 .
.
where ![]() is the total population.
is the total population.
And , represent the rate of change or the population densities of Susceptible, InfectedRemoved, prevented and controlled at time t respectively.
, represent the rate of change or the population densities of Susceptible, InfectedRemoved, prevented and controlled at time t respectively.
Susceptible are individuals that are not infected with the disease yet, infected are individuals that are infected with the disease and can transmit it to susceptible, Removed are the individuals that are infected and are receiving ART, Prevented are infected individuals using condom, and Controlled are infected individuals receiving Antiretroviral therapy and using condom.
And b is natural death rate, B is the incidence rate,  is the natural death rate and the same in all compartments, σ is the proportion of infected individuals that received ART, λ is the proportion of infected individuals that used the condom, ρ is the proportion of infected individuals that received ART first and later used the condom, π is the proportion of infected individuals that used the condom first and later received ART.
is the natural death rate and the same in all compartments, σ is the proportion of infected individuals that received ART, λ is the proportion of infected individuals that used the condom, ρ is the proportion of infected individuals that received ART first and later used the condom, π is the proportion of infected individuals that used the condom first and later received ART.
The incidence rate ![]() at time t is given by
at time t is given by
 (3.16)
(3.16)
3.3. Stability Analysis of the Equilibrium States
Here we would establish the general stability of the disease free equilibrium (DFE) states, by considering the model parameters and using the model equations. Since we have five systems of nonlinear equations, we know that it is almost impossible to obtain an analytical solution to these systems; therefore, we use the idea of Kimbir et al., (2008) [3] , Muhammad, (2010) [4] and Hethcote, (1989) [6] .
3.3.1. The Sub-Model without ART/Condom (i.e. )
)
The sub model equations are:
 (3.17)
(3.17)
The equilibrium points of the above equations are given by thus:
 , since I = 0 thus the DFE state exists. We examine its stability using Routh-Hurwitz stability condition. The Jacobian matrix is:
, since I = 0 thus the DFE state exists. We examine its stability using Routh-Hurwitz stability condition. The Jacobian matrix is:

If  are the eigenvalues of the matrix
are the eigenvalues of the matrix  then
then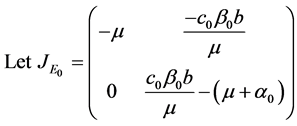
We would have for stability

Only when  since all the parameters are non-negative. The trace of the matrix
since all the parameters are non-negative. The trace of the matrix  is negative only if
is negative only if . Even then, it failed satisfy the required conditions for stability of the DFE state. Thus the DFE is not stable. Hence there is an endemic equilibrium (EE)
. Even then, it failed satisfy the required conditions for stability of the DFE state. Thus the DFE is not stable. Hence there is an endemic equilibrium (EE)
state  which is locally asymptotically stable, meaning that the infection would persist in the absent of ART and Condom.
which is locally asymptotically stable, meaning that the infection would persist in the absent of ART and Condom.
3.3.2. The Sub-Model with Only the Infected Individuals Receiving ART (i.e. σ ≠ 0, λ = 0)
The sub model equations are thus:
 (3.18)
(3.18)
The equilibrium points are ![]()

The community matrix corresponding to this state is

This implies that the entire expression would be non-negative, that is, if the infected individuals received ART the DFE state would be stable provided these threshold conditions hold. Please observe, also the trace (trace of a matrix is the sum of the diagonal of the matrix) of the matrix  would be negative following the same argument. Hence the DFE state is locally asymptotically stable under this extreme condition.
would be negative following the same argument. Hence the DFE state is locally asymptotically stable under this extreme condition.
3.3.3. The Submodel with Only Infected Individuals Using Condom (i.e. σ = 0, λ ≠ 0)
The resulting submodel equations are as follows:
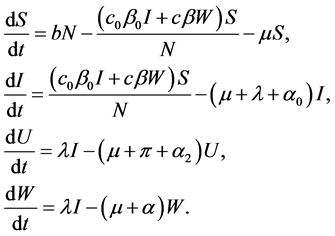 (3.19)
(3.19)
The DFE state is 
The Jacobian matrix corresponding to this state is
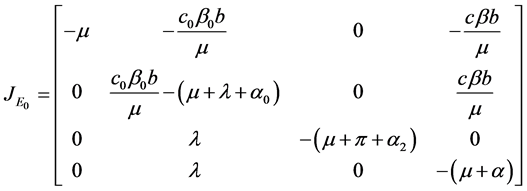



This means that the trace of the contact matrix would be negative, that is, if the infected individuals used condom the DFE state would be stable provided these threshold conditions hold.
3.3.4. The Sub Model with the Infected Individuals USING Both ART/Condom (i.e. σ ≠ 0, λ ≠ 0)
The resulting equations are:
 (3.20)
(3.20)
Please observe that here the entire model equations are involved, therefore, we use the basic reproduction ratio of the infective to discuss the stability of the general model to avoid algebraic complexity involved in the computation of the Routh-Hurwitz stability method. In adopting this approach we use the idea of the next generation operator by Muhammad, (2010) [4] , Hethcote, (1989) [6] and Diekmann et al., (1990) [7] . We categorize the population into two classes as follows:
 (3.21)
(3.21)
Then we have thus:
 (3.22)
(3.22)
and
 (3.23)
(3.23)
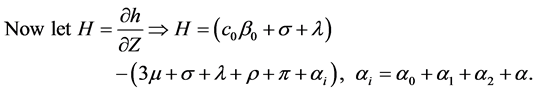 (3.24)
(3.24)
Letting![]() , with M* > 0, D* > 0 is a diagonal matrixThen
, with M* > 0, D* > 0 is a diagonal matrixThen  and
and 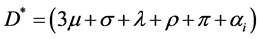
The basic reproduction number of the infective is defined as the spectral radius (dominant eigenvalues) of the matrix M*D*‒1.
Thus, (3.25)
(3.25)
for stability of the DFE state, we have;
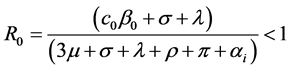 , which is consistent. Thus the DFE state is locally asymptotically stable and the disease would not persist, it would die out, if the threshold parameters satisfy this condition, while for
, which is consistent. Thus the DFE state is locally asymptotically stable and the disease would not persist, it would die out, if the threshold parameters satisfy this condition, while for  , we have an EE state which is locally asymptotically stable.
, we have an EE state which is locally asymptotically stable.
4. Conclusion
The main result of the study is found in section three, where threshold conditions are given for the stability of the disease-free and the endemic equilibrium states of the model. Whereas the condition  holds vacuously, the reproduction number
holds vacuously, the reproduction number

is strictly less than 1. From the right hand side of the expression for R0, we see that increasing the value of σ, λ, ρ and π (i.e. increasing the treatment rates) reduces the value of R below 1. Similarly, reducing the value of c0 and  may achieve the same purpose. Thus, for an effective ART/condom programme, it may be necessary to also reduce the transmission probability and the average number of sexual partners of the infected individuals. These can be done through counseling and education. From the expression R0 < 1, we see that the minimum proportion of infected individuals to receive ART/condom is
may achieve the same purpose. Thus, for an effective ART/condom programme, it may be necessary to also reduce the transmission probability and the average number of sexual partners of the infected individuals. These can be done through counseling and education. From the expression R0 < 1, we see that the minimum proportion of infected individuals to receive ART/condom is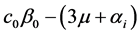 .
.
References
- Centers for Disease Control and Prevention (1989) Perspectives in Disease Prevention and Health Promotion Condoms for Prevention of Sexually Transmitted Diseases.
- Tinuola, F.R., Ayodele J.O. and Ola, T.M. (2006) HIV/AIDS in Africa and the Politics of the West. Nigerian Journal of Social Research, 1, 100-112.
- Kimbir A.R. and Oduwole, H.K (2008)A Mathematical Model of HIV/AIDS Transmission Dynamics Considering Counselling and Antiretroviral Therapy. Journal of Modern Mathematics and Statistics, 2, 166-169.
- Muhammad, A.Y. (2010) A Mathematical Model of HIV Transmission Dynamics Considering the Use of Antiretroviral Therapy and a Preventive Measure (Condom). M.Sc Thesis (Unpublished).
- Yang H.M. and Ferreira, W.C. (1999) A Population Model Applied to HIV Transmission, Considering Protection and Treatment. IMA Journal of Mathematics Applied in Medicine and Biology, 16, 237-259.
- Hethcote, H.W. (1989) Three Basic Epidemiological Models. Applied Mathematical Ecology. Springer-Verlag, Berlin, 119-144. http://dx.doi.org/10.1007/978-3-642-61317-3_5
- Diekmann, O., Heesterbeek, J.P. and Metz, J.A. (1990) On the Definition and the Computation of the Basic Reproduction Ratio R0 in Models for Infectious Diseases in Heterogeneous Populations. Journal of Mathematical Biology, 28, 365-382. http://dx.doi.org/10.1007/BF00178324

