Communications and Network
Vol.5 No.2(2013), Article ID:30983,8 pages DOI:10.4236/cn.2013.52011
Effective Capacity and Interference Analysis in Multiband Dynamic Spectrum Sensing
Electrical and Computer Engineering Department, Ryerson University, Toronto, Canada
Email: melalem@ryerson.ca, lzhao@ee.ryerson.ca
Copyright © 2013 Mohamed Elalem, Lian Zhao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 11, 2013; revised March 11, 2013; accepted April 11, 2013
Keywords: Effective Capacity; Cognitive Radio; Multiband Sensing; Interference
ABSTRACT
In this paper, the performance of multichannel transmission in cognitive radio is studied. Both  constraints and interference limitations are considered. The activities of the primary users (PU)s are initially detected by cognitive users (CU)s who perform sensing process over multiple channels. They transmit in a single channel at variable power and rates depending on the channel sensing decisions and the fading environment. The cognitive operation is modeled as a state transition model in which all possible scenarios are studied. The
constraints and interference limitations are considered. The activities of the primary users (PU)s are initially detected by cognitive users (CU)s who perform sensing process over multiple channels. They transmit in a single channel at variable power and rates depending on the channel sensing decisions and the fading environment. The cognitive operation is modeled as a state transition model in which all possible scenarios are studied. The  constraint of the cognitive users is investigated through statistical analysis. Analytical form for the effective capacity of the cognitive radio channel is found. Optimal power allocation and optimal channel selection criterion are obtained. Impact of several parameters on the transmission performance, as channel sensing parameters, number of available channels, fading and other, are identified through numerical example.
constraint of the cognitive users is investigated through statistical analysis. Analytical form for the effective capacity of the cognitive radio channel is found. Optimal power allocation and optimal channel selection criterion are obtained. Impact of several parameters on the transmission performance, as channel sensing parameters, number of available channels, fading and other, are identified through numerical example.
1. Introduction
Much interest in cognitive radio systems is raised due to their ability to utilize the available spectrum much more effectively. In addition to efficient spectrum utilization, it is more important in wireless systems to provide reliable communications while preserving a certain level of quality-of-service  In cognitive radio systems, challenges in providing
In cognitive radio systems, challenges in providing  assurances increase due to the fact that cognitive users should operate under constraints on the interference levels that they produce to primary users. For the secondary users, these interference constraints lead to variations in transmit power levels and channel accesses. This discontinuing in accessing the channels due to the activity of primary users make it difficult for the cognitive users to satisfy their own
assurances increase due to the fact that cognitive users should operate under constraints on the interference levels that they produce to primary users. For the secondary users, these interference constraints lead to variations in transmit power levels and channel accesses. This discontinuing in accessing the channels due to the activity of primary users make it difficult for the cognitive users to satisfy their own  requirement. The authors in [1] proposed a
requirement. The authors in [1] proposed a  constrained power and rate allocation scheme for spectrum sharing systems in which it was guaranteed a minimumrate to the primary user for a certain percentage of time. The same authors, in [2], considered variable-rate variable-power modulation employed under delay
constrained power and rate allocation scheme for spectrum sharing systems in which it was guaranteed a minimumrate to the primary user for a certain percentage of time. The same authors, in [2], considered variable-rate variable-power modulation employed under delay  constraints over spectrum-sharing channels. Various capacity metrics, e.g., ergodic, outage, and minimum-rate capacity for the cognitive channels with interference constraints in Rayleigh fading environments, have been studied in these papers.
constraints over spectrum-sharing channels. Various capacity metrics, e.g., ergodic, outage, and minimum-rate capacity for the cognitive channels with interference constraints in Rayleigh fading environments, have been studied in these papers.
In this paper, the effective capacity of cognitive radio channels is studied where the cognitive radio detects the activity of the primary users in a multichannel case, and it performs data transmission in one of these channels using both rate and power adaptation that depends on the channel conditions and the activity of the primary users. An average interference constraint on the cognitive users is formulated. Maximum throughput formula is obtained through the effective capacity approach. Optimal power allocation is derived and investigated through numerical results.
The rest of the paper is organized as follows. In Section 2, the system model and assumptions are given. Channel capacity and state transition model are formulated and constructed in Section 3. Section 4 discusses outage constraints and interference limit. In Section 5, the effective capacity for the cognitive user is formally defined in terms of  constraints and then formulated and optimized. Channel selection criterion is proposed in Section 6. Numerical results are provided in Section 7, and the paper is concluded in Section 8.
constraints and then formulated and optimized. Channel selection criterion is proposed in Section 6. Numerical results are provided in Section 7, and the paper is concluded in Section 8.
2. System Model and Assumptions
The considered system model consists of cognitive radio network in which the cognitive users sense  channels with a bandwidth
channels with a bandwidth  for each, where
for each, where  among them the cognitive users choose a channel for data transmission. The channel sensing and data transmission are performed in frames of duration
among them the cognitive users choose a channel for data transmission. The channel sensing and data transmission are performed in frames of duration![]() . It is assumed that
. It is assumed that ![]() seconds is allocated for channel sensing while the remaining
seconds is allocated for channel sensing while the remaining  seconds are allocated for data transmission. The primary user activity influences the transmission power and rate levels. If all of the channels are detected as busy, the cognitive transmitter selects one channel according to a certain criterion, and sets the transmission power and rate to
seconds are allocated for data transmission. The primary user activity influences the transmission power and rate levels. If all of the channels are detected as busy, the cognitive transmitter selects one channel according to a certain criterion, and sets the transmission power and rate to  and
and , where
, where  denotes the time index in the transmission frame. In the contrary, if at least one channel is sensed to be idle, data transmission is sent with power
denotes the time index in the transmission frame. In the contrary, if at least one channel is sensed to be idle, data transmission is sent with power  at rate
at rate . In the case of multiple channels are detected as idle, one idle channel is selected according to a certain policy explained later.
. In the case of multiple channels are detected as idle, one idle channel is selected according to a certain policy explained later.
The channel fading coefficient between the cognitive transmitter and the receiver with an arbitrary distribution is assumed as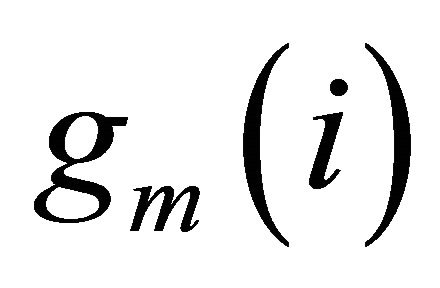 . A block-fading channel model is assumed in which the fading coefficients stay constant in the frame, and they may change from one block to another independently in each channel. The active primary user’s signal arriving at the cognitive receiver is assumed to have zero mean and a variance
. A block-fading channel model is assumed in which the fading coefficients stay constant in the frame, and they may change from one block to another independently in each channel. The active primary user’s signal arriving at the cognitive receiver is assumed to have zero mean and a variance . The background noise at the receivers is modeled as a zero-mean, circularly symmetric, complex Gaussian random variable with variance
. The background noise at the receivers is modeled as a zero-mean, circularly symmetric, complex Gaussian random variable with variance .
.
Perfect Channel State Information (CSI) is assumed at each receiver. It is further assumed that each channel has a bandwidth that is equal to the coherence bandwidth . With this assumption, it can be supposed that independent flat fading is experienced in each channel.
. With this assumption, it can be supposed that independent flat fading is experienced in each channel.
3. Channel Capacity and State Transition Model
In order to further simplify the setting, it is considered a symmetric model in which fading coefficients are identically distributed in different channels. Moreover, the background noise and primary users’ signals are also assumed to be identically distributed in different channels and hence their variances  and
and  do not depend on m. So the subscript m can be omitted. The probability of each channel being occupied by the primary users is assumed to be the same and equal to
do not depend on m. So the subscript m can be omitted. The probability of each channel being occupied by the primary users is assumed to be the same and equal to  In channel sensing process, the same energy threshold is assumed in each channel.
In channel sensing process, the same energy threshold is assumed in each channel.
Due to possible error in channel sensing, we may have the following possible cases:
•  :
:  bands are sensed as busy, and the selected channel is actually busy.
bands are sensed as busy, and the selected channel is actually busy.
•  :
:  bands are sensed as busy, and the selected channel is actually idle.
bands are sensed as busy, and the selected channel is actually idle.
•  :
:  band(s) is sensed as idle, and the selected channel is actually busy.
band(s) is sensed as idle, and the selected channel is actually busy.
• 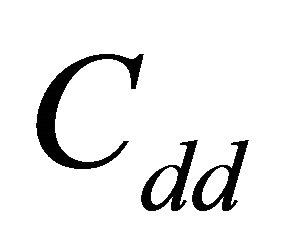 :
:  band(s) is sensed as idle, and the selected channel is actually idle, where
band(s) is sensed as idle, and the selected channel is actually idle, where .
.
By the assumption of that the state transitions occur every frame, the probability of the channel detected as busy can be written as
 (1)
(1)
where , and
, and  are the probabilities of detection and false alarm. The probabilities of being in each of the above cases are summarized in Table 1.
are the probabilities of detection and false alarm. The probabilities of being in each of the above cases are summarized in Table 1.
In each of the above cases, we have two states, namely either  state in which the instantaneous transmission rate exceeds the instantaneous channel capacity, or
state in which the instantaneous transmission rate exceeds the instantaneous channel capacity, or  state if it does not. Assuming the interference caused by the primary users
state if it does not. Assuming the interference caused by the primary users  as additional Gaussian noise, the instantaneous channel capacities for the above four cases can be expressed as follows
as additional Gaussian noise, the instantaneous channel capacities for the above four cases can be expressed as follows
 (2)
(2)
where  refers to the possible case and
refers to the possible case and  represents the
represents the  for the corresponding case in the
for the corresponding case in the  channel which is given by
channel which is given by
 (3)
(3)
where  and
and  represent the total noise when a channel is busy and idle respectively.
represent the total noise when a channel is busy and idle respectively.
For the cases  and
and , the cognitive transmitter detects all channels as busy and transmits with rate
, the cognitive transmitter detects all channels as busy and transmits with rate
 (4)
(4)
While for the cases  and
and , at least one channel is sensed as idle and the transmission rate is
, at least one channel is sensed as idle and the transmission rate is
 (5)
(5)
whereas the transmitter assumes the channel as idle, it

Table 1. The probability of being in each four cases.
sets the power level to  and it supposes that no interference from the primary transmissions will be produced as seen by nonexistence of
and it supposes that no interference from the primary transmissions will be produced as seen by nonexistence of  in the denominator of
in the denominator of .
.
The transmission rate for the cases  and
and  is less than or equal to the instantaneous channel capacity. Reliable transmission at rate
is less than or equal to the instantaneous channel capacity. Reliable transmission at rate 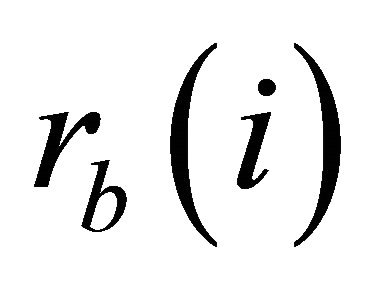 is achieved and channel is in the
is achieved and channel is in the  state. Similarly, the channel is in the
state. Similarly, the channel is in the  state in the case
state in the case  in which the transmission rate is
in which the transmission rate is . While in the case
. While in the case , the channel is in the
, the channel is in the  state because the transmission rate exceeds the instantaneous channel capacity (i.e.,
state because the transmission rate exceeds the instantaneous channel capacity (i.e., ). Hence, reliable communication cannot be established.
). Hence, reliable communication cannot be established.
Referring to the above discussion, the cognitive transmission model can constructed as depicted in Figure 1. We have  states model, consisting of
states model, consisting of 
 states and one
states and one  state. The first
state. The first  state represents the
state represents the  states in the cases
states in the cases  and
and , in both of which the transmission power and rate are
, in both of which the transmission power and rate are  and
and  respectively. All channels are sensed as busy in this state. The remaining
respectively. All channels are sensed as busy in this state. The remaining  states from 2 to
states from 2 to  can be represented as the expansion of the
can be represented as the expansion of the  state in the cases
state in the cases 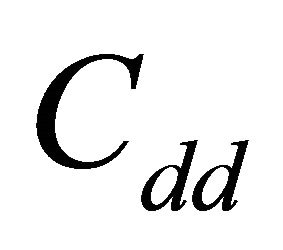 in which at least one channel is sensed as idle and the selected channel for transmission is really idle. More specifically, the
in which at least one channel is sensed as idle and the selected channel for transmission is really idle. More specifically, the 
 state for
state for  is the
is the  state in which
state in which  channels are sensed as idle and the channel selected for transmission is actually idle. The transmission power and rate for these states are
channels are sensed as idle and the channel selected for transmission is actually idle. The transmission power and rate for these states are  and
and 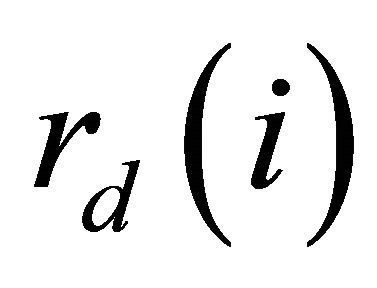 respectively.
respectively.
The single 
 state represents the case
state represents the case  in which transmission rate exceeds the instantaneous channel capacity.
in which transmission rate exceeds the instantaneous channel capacity.
The state transition probabilities can be analyzed as-

Figure 1.  ON states and one OFF state for the cognitive radio channel and their corresponding state transition probabilities.
ON states and one OFF state for the cognitive radio channel and their corresponding state transition probabilities.
suming that the PU’s activity is independent among the channels and also from one frame to another as mentioned above. The probability of staying in the first  state in which all channels are sensed as busy can be easily expressed as
state in which all channels are sensed as busy can be easily expressed as . Again with this assumption of independence over the frames, the state transition probabilities are independent on the originating state, so the transition probabilities
. Again with this assumption of independence over the frames, the state transition probabilities are independent on the originating state, so the transition probabilities  are similar and equal to
are similar and equal to . For
. For  the transition probabilities are obtained as
the transition probabilities are obtained as
 (6)
(6)
where  is the Binomial coefficient.
is the Binomial coefficient.
The transition probabilities for the  state are
state are
 (7)
(7)
where we use the power series relation in [3,4].
 (8)
(8)
From the above definitions, it can be seen that the state transition probability matrix is  with a rank of 1.
with a rank of 1.
4. Outage Constraints and Interference Limit
To adapt the transmission powers of the CRs and ensuring not producing any harmful on the primary users, interference power constraints is analyzed in this section. From the considered system model, it can be included that the interference to the primary users is caused only in the cases  and
and . Where, in the case
. Where, in the case , the channel is actually busy, and the cognitive user, detecting the channel as busy, transmits at power level
, the channel is actually busy, and the cognitive user, detecting the channel as busy, transmits at power level . The instantaneous interference power introduced on the primary user is
. The instantaneous interference power introduced on the primary user is , where
, where  is the fading coefficient of the channel between the cognitive transmitter and the primary user.
is the fading coefficient of the channel between the cognitive transmitter and the primary user.
For the case , although the channel is actually busy, the secondary user, detecting the channel as idle, transmits at power
, although the channel is actually busy, the secondary user, detecting the channel as idle, transmits at power . The instantaneous interference power is
. The instantaneous interference power is  in this case. Since power adaption is considered, transmission power levels
in this case. Since power adaption is considered, transmission power levels  and
and  in general vary with
in general vary with  and
and![]() , which is the power of the fading coefficient between the secondary transmitter and secondary receiver in the chosen transmission channel.
, which is the power of the fading coefficient between the secondary transmitter and secondary receiver in the chosen transmission channel.
In the cases:  and
and , the instantaneous interference power levels depend on both
, the instantaneous interference power levels depend on both  and
and ![]() whose distributions depend on number of available channels from which the selection is performed. For this reason, it is necessary in the case
whose distributions depend on number of available channels from which the selection is performed. For this reason, it is necessary in the case  to separately consider the individual cases with different number of idle-detected channels. For instance, in the
to separately consider the individual cases with different number of idle-detected channels. For instance, in the  case for
case for 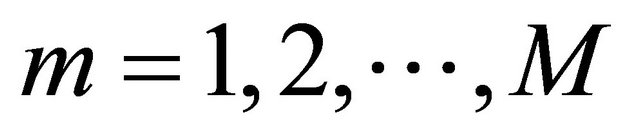 , there are
, there are ![]() channels detected as idle and the channel chosen out of these
channels detected as idle and the channel chosen out of these ![]() channels is actually busy.
channels is actually busy.
The average interference has to be constrained to the value . This can be formulated as
. This can be formulated as

This yields to
 (9)
(9)
The expectations should be taken over the distributions of ![]() and
and  and over the probabilities of different cases. The term
and over the probabilities of different cases. The term  in Equation (9) depends on the number of idle-detected channels,
in Equation (9) depends on the number of idle-detected channels,![]() .
.
5. Effective Capacity for Cognitive User
The Effective Capacity  (or Effective Bandwidth) theory is a powerful approach to evaluate the capability of a wireless channel to support data transmissions with diverse statistical quality of service
(or Effective Bandwidth) theory is a powerful approach to evaluate the capability of a wireless channel to support data transmissions with diverse statistical quality of service  guarantees [5-7]. It is defined as the maximum constant arrival rate that can be supported by a given channel service process while meeting the
guarantees [5-7]. It is defined as the maximum constant arrival rate that can be supported by a given channel service process while meeting the  requirement [5]. In particular, the statistical
requirement [5]. In particular, the statistical  guarantee can be characterized by a metric called
guarantee can be characterized by a metric called  exponent denoted by
exponent denoted by  [5]. The
[5]. The  exponent
exponent characterizes the exponentially decaying rate of the violation probability against the queue-length threshold. With the pair (Effective Capacity
characterizes the exponentially decaying rate of the violation probability against the queue-length threshold. With the pair (Effective Capacity  and
and  exponent
exponent ), it can be observed insight tradeoff between the delay
), it can be observed insight tradeoff between the delay  requirement and the system throughput. Higher
requirement and the system throughput. Higher  represents more stringent delay
represents more stringent delay  requirements, and vice versa.
requirements, and vice versa.
The effective capacity for a given θ is defined in [5] as
 (10)
(10)
where  is a function that depends on the natural logarithm of the moment generating function of
is a function that depends on the natural logarithm of the moment generating function of , and
, and 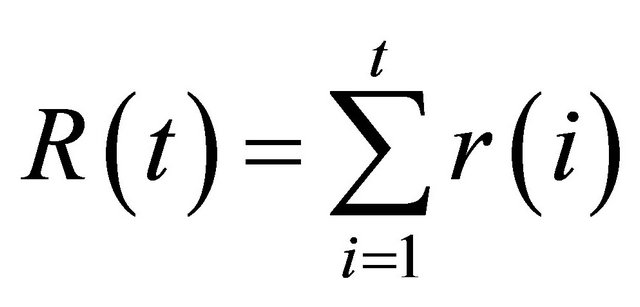 is the time-accumulated service process.
is the time-accumulated service process.  is the expectation with respect to
is the expectation with respect to .
.
It can be noticed that the service rate is  if the cognitive user is in state 1 at band m. Similarly, the service rate is
if the cognitive user is in state 1 at band m. Similarly, the service rate is  in states between 2 and
in states between 2 and . In the remained state i.e.,
. In the remained state i.e.,  state, reliable connection can not be achieved because the instantaneous transmission rate exceeds the instantaneous channel capacities, so the service rates in this state is zero.
state, reliable connection can not be achieved because the instantaneous transmission rate exceeds the instantaneous channel capacities, so the service rates in this state is zero.
The normalized effective capacity (in bits/s/Hz or 1/nat) under the average interference power constraint Equation (9) can be formulated as the following optimization problem
 (11)
(11)
s.t. Equation (9) holds, where  for
for  are the state transition probabilities defined in Section 3. The maximization operator is with respect to the power adaptations
are the state transition probabilities defined in Section 3. The maximization operator is with respect to the power adaptations  and
and .
.
Note that the expectation  in the objective function and
in the objective function and  in the constraint of the above optimization problem are with respect to the joint distribution of
in the constraint of the above optimization problem are with respect to the joint distribution of 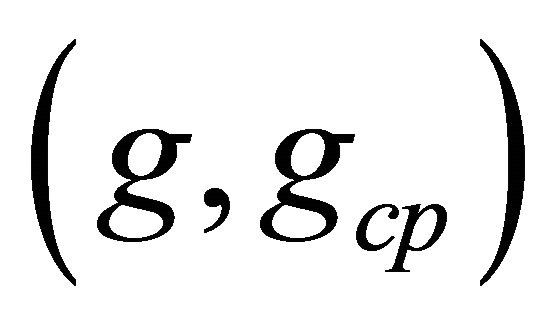 of the channel selected for transmission when all channels are sensed busy. The expectations
of the channel selected for transmission when all channels are sensed busy. The expectations  and
and  are with respect to the joint distribution of
are with respect to the joint distribution of  of the channel selected for transmission when
of the channel selected for transmission when ![]() channels are sensed as idle.
channels are sensed as idle.
To identify the optimal power allocation that the cognitive users should employ, the problem in Equation (11) can be converted to a minimization problem using the fact that logarithmic function is a monotonic function (Equation (12)). s.t. Equation (9) holds.
This objective function is strictly convex and the constraint function in Equation (11) is linear with respect to  and
and . This can be concluded from the fact that strict convexity follows from the strict concavity of
. This can be concluded from the fact that strict convexity follows from the strict concavity of ![]() and
and  in Equations (4) and (5) with respect to
in Equations (4) and (5) with respect to  and
and , strict convexity of the exponential function, and the fact that the weighted sum of strictly convex functions is strictly convex [8,9]. Using Lagrangian method, the power allocation can be expressed as
, strict convexity of the exponential function, and the fact that the weighted sum of strictly convex functions is strictly convex [8,9]. Using Lagrangian method, the power allocation can be expressed as
 (13)
(13)
and
 (14)
(14)
where  and
and

Using these optimal transmission powers, the effective capacity can be expressed in integral form as Equation (15).
6. Selection Criterion in Rayleigh Fading Channel
We aim present a criterion with which the transmission channel is selected from a set of available channels. Since the terms  and
and  in Equation (13)
in Equation (13)
are monotonically decreasing functions of . The term:
. The term:

is increasing function. It can be observed from Equation (15) that the effective capacity depends only on the channel power ratio , and it is increasing with increaseing this power ratio. Therefore, the criterion for choosing the transmission band among multiple busy bands unless there is no idle band detected, or among multiple idle bands if there are idle bands detected should be based on this ratio of the channel gains. Clearly, the policy that maximizes the effective capacity is to choose the channel with the highest ratio of
, and it is increasing with increaseing this power ratio. Therefore, the criterion for choosing the transmission band among multiple busy bands unless there is no idle band detected, or among multiple idle bands if there are idle bands detected should be based on this ratio of the channel gains. Clearly, the policy that maximizes the effective capacity is to choose the channel with the highest ratio of . This also intuitively leads to a result that as we want to maximize
. This also intuitively leads to a result that as we want to maximize ![]() to improve the secondary transmission and at the same time minimize
to improve the secondary transmission and at the same time minimize  to diminish the interference caused to the primary users. Maximizing
to diminish the interference caused to the primary users. Maximizing  provides us the problem key in the channel selection algorithm.
provides us the problem key in the channel selection algorithm.
Let  where
where  is the ratio of the gains in the
is the ratio of the gains in the  band channel. All these ratios are assumed to be independent and identical distributed.
band channel. All these ratios are assumed to be independent and identical distributed.
Statistically if , where
, where  are independent and identically distributed random variables with pdf of
are independent and identically distributed random variables with pdf of  then the cdf and
then the cdf and  of
of ![]() are given as (Theorem 5.7 in [10])
are given as (Theorem 5.7 in [10])
 (16)
(16)
 (17)
(17)
Using this fact, we can express the pdf of ![]() as
as
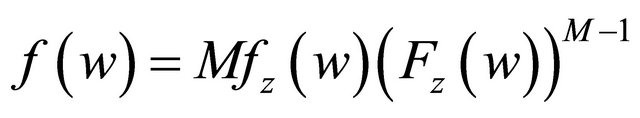 (18)
(18)
where  and
and  are the
are the  and
and  of the gain ratio
of the gain ratio  in one channel, respectively.
in one channel, respectively.
Now, the first integral in Equation (15) can be evaluated with respect to this distribution.
Similarly, Let  for
for
 . The
. The  of
of  can be expressed as follows:
can be expressed as follows:
 (19)
(19)
The second integral of Equation (15) can be evaluated

using this distribution, and by using the power series property [3]:

The analysis in the preceding sections applies for arbitrary joint distributions of ![]() and
and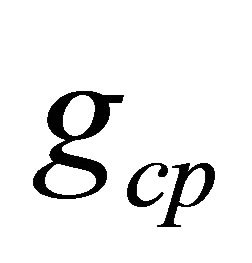 . Channel fading is assumed here to be Rayleigh fading in which the power gains
. Channel fading is assumed here to be Rayleigh fading in which the power gains ![]() and
and  are exponentially distributed. We further assume that these fading are mutually independent and each has unit-mean. Statistically, if there are two independent exponentially distributed variables
are exponentially distributed. We further assume that these fading are mutually independent and each has unit-mean. Statistically, if there are two independent exponentially distributed variables 
and![]() , the random variable
, the random variable  has the
has the 
 (20)
(20)
So, the  of
of ![]() in Equations (18) and (19) can be expressed as
in Equations (18) and (19) can be expressed as
 (21)
(21)
Using Equations (6), (7), (15), (21), the effective capacity formula for Rayleigh fading channel can be written as in (22), where  . The impact of several parameters on the effective capacity is investigated through the following numerical example (Equation (22)).
. The impact of several parameters on the effective capacity is investigated through the following numerical example (Equation (22)).
7. Numerical Example
In this section, several numerical results for the obtained effective capacity expression will be investigated. The impact of channel sensing parameters and the average interference constraints are illustrated. The frame duration is  with
with  of this time is conserved for sensing process. The prior probability of the channel being busy is the same for all channels and set to
of this time is conserved for sensing process. The prior probability of the channel being busy is the same for all channels and set to . All variances are set to unity. The channel bandwidth is
. All variances are set to unity. The channel bandwidth is .
.
Figure 2, shows the effective capacity vs detection probability , for different number of channels
, for different number of channels  when the interference constraint is normalized by the noise power. As
when the interference constraint is normalized by the noise power. As  increases, the effective capacity increases due to the fact that more reliable detection of the activity primary users leads to fewer miss-detection. It can also be seen that the highest effective capacity is attained when
increases, the effective capacity increases due to the fact that more reliable detection of the activity primary users leads to fewer miss-detection. It can also be seen that the highest effective capacity is attained when . Hence, the cognitive users does not benefit from the availability of multiple channels. This is especially pronounced for high values of
. Hence, the cognitive users does not benefit from the availability of multiple channels. This is especially pronounced for high values of . Although several parameters affect the value of the effective capacity, one explanation for this observation is that the probabilities of the cases
. Although several parameters affect the value of the effective capacity, one explanation for this observation is that the probabilities of the cases  and
and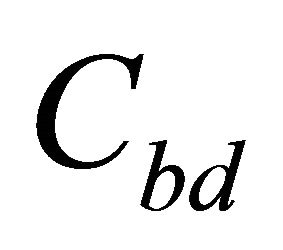 , in which the cognitive users transmit with power
, in which the cognitive users transmit with power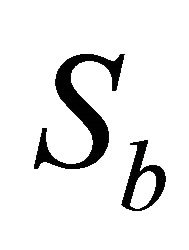 , decrease with increasing
, decrease with increasing , while the probabilities of the cases
, while the probabilities of the cases  and
and  in which the cognitive users transmit with
in which the cognitive users transmit with ![]() ower
ower , increase.
, increase.
In Figure 3, the effect of the primary user’s occupancy  on the effective capacity is investigated for different number of sensed channels. This effect is observable for relatively small detection probability. While for higher ( i.e. ,
on the effective capacity is investigated for different number of sensed channels. This effect is observable for relatively small detection probability. While for higher ( i.e. , ), the improvement in the effective capacity decreases. This is most likely true for all
), the improvement in the effective capacity decreases. This is most likely true for all . For
. For , higher
, higher  attached with higher
attached with higher 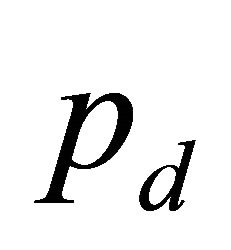 indicate to most likely of the presence of the primary user and hence less capacity can be achieved by the cognitive user as can be seen from the figure.
indicate to most likely of the presence of the primary user and hence less capacity can be achieved by the cognitive user as can be seen from the figure.
Figure 4 examines the impact of the  exponent values,
exponent values,  for
for . This figure confirms that significant capacity gains can be achieved for lossy
. This figure confirms that significant capacity gains can be achieved for lossy  constraints (i.e., small
constraints (i.e., small ). While the capacity decreases dramatically for highly strength
). While the capacity decreases dramatically for highly strength  constraints.
constraints.
In Figure 5, the effective capacity is plotted versus the interference threshold  for different number of channels. The probability of detection is sit at
for different number of channels. The probability of detection is sit at . The figure shows that as the interference gets more strict (i.e.,
. The figure shows that as the interference gets more strict (i.e.,  becomes smaller), a higher number of channels is needed to maximize the effective capacity.
becomes smaller), a higher number of channels is needed to maximize the effective capacity.
As an example, if the interference threshold  , then five channels are needed to reach maximum capacity, while if the interference threshold
, then five channels are needed to reach maximum capacity, while if the interference threshold  , one channel is enough to get the highest throughput. As it is mentioned before, increasing the number of available channels from which the transmission channel is selected provides no benefit or can even degrade the performance of the cognitive users. On the other hand, it always provides benefits to the primary users in the sense of lowering the probability of interference.
, one channel is enough to get the highest throughput. As it is mentioned before, increasing the number of available channels from which the transmission channel is selected provides no benefit or can even degrade the performance of the cognitive users. On the other hand, it always provides benefits to the primary users in the sense of lowering the probability of interference.


Figure 2. Effective capacity vs probability of detection for different number of channels in the Rayleigh fading channel.

Figure 3. Normalized effective capacity vs probability of detection for different number of channels and different primary probabilities 
 Dashed curves represent for the
Dashed curves represent for the 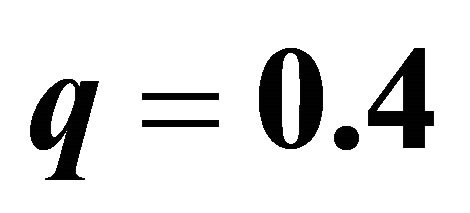 case and solid curves represent the
case and solid curves represent the  case relevant colors.
case relevant colors.

Figure 4. Effective capacity vs probability of detection for different  exponent delay
exponent delay .
.
8. Conclusion
The performance of cognitive transmission under  and interference constraints is studied. Cognitive users
and interference constraints is studied. Cognitive users

Figure 5. Effective capacity vs  for different number of channels in the Rayleigh fading channel, Pd = 0.8
for different number of channels in the Rayleigh fading channel, Pd = 0.8 .
.
are assumed to perform sensing in multiple channels and then select a single channel for transmission with rate and power that depend on both sensing outcomes and fading distribution. A state transition model for this cognitive operation has been constructed. All possible cases and states are considered and analyzed. Interference constraint is statistically analyzed and formulated. Maximum throughput formulas for the cognitive users are obtained. Selection criterion that maximizes the capacity is proposed for arbitrary channel fading then it is applied for Rayleigh distribution. The optimal power allocation is also determined. Sensing multiple bands brings advantages only under strict interference requirements and it reduces the probability of a primary user to be interfered.
REFERENCES
- L. Musavian and S. Aissa, “Quality-of-Service Based Power Allocation in Spectrum-Sharing Channels,” IEEE Global Communication Conference GOLBCOM, New Orleans, 30 November-4 December 2008.
- L. Musavian and S. Aissa, “Adaptive Modulation in Spectrum-Sharing Systems with Delay Constraints,” IEEE International Conference on Communications ICC, Dresden, 14-18 June 2009.
- W. Magnus, F. Oberhettinger and F. Tricomi, “Higher Transcendental Functions,” McGraw Hill, New York, 1982.
- Wolfram Mathematica, the Web’s Most Extensive Mathematics Recourses. http://mathworld.wolfram.com
- D. Wu and R. Negi, “Effective Capacity: A Wireless Link Model for Support of Quality of Service,” IEEE Transactions on Wireless Communication, Vol. 2, No. 4, 2003, pp. 630-643.
- E. Jorswieck, R. Mochaourab and M. Mittelbach, “Effective Capacity Maximization in Multi-Antenna Channels with Covariance Feedback,” IEEE Transactions on Wireless Communication, Vol. 9, No. 10, 2010, pp. 2988- 2993. doi:10.1109/TWC.2010.080210.091060
- L. Musavian, S. Aïssa and S. Lambotharan, “Effective Capacity for Interference and Delay Constrained Cognitive Radio Relay Channels,” IEEE Transactions on Wireless Communication, Vol. 9, No. 5, 2010, pp. 1698-1707. doi:10.1109/TCOMM.2010.05.090600
- S. Boyd and L. Vandenberghe, “Convex Optimization,” 7th Edition, Cambridge University Press, Cambridge, 2009.
- D. Bertsekas, “Convex Analysis and Optimization,” Athena Scientific, Belmont, 2003.
- R. Yates and D. Goodman, “Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers,” 2nd Edition, John Wiley & Sons, Hoboken, 2005, pp. 257-264.

