Communications and Network
Vol.3 No.3(2011), Article ID:6773,6 pages DOI:10.4236/cn.2011.33015
An Improved MPH-Based Delay-Constrained Steiner Tree Algorithm
1College of Mathematics and Physics, Chongqing University of Posts and Telecommunication, Chongqing, China
2College of Computer Science and Technology, Chongqing University of Posts and Telecommunication, Chongqing, China
E-mail: khuan222@126.com
Received May 31, 2011; revised June 20, 2011; accepted June 29, 2011
Keywords: Multicast Tree, Delay-Constrained, Steiner Tree
Abstract
In order to optimize cost and decrease complexity with a delay upper bound, the delay-constrained Steiner tree problem is addressed. Base on the new delay-constrained MPH (DCMPH_1) algorithm and through improving on the select path, an improved MPH-based delay-constrained Steiner tree algorithm is presented in this paper. With the new algorithm a destination node can join the existing multicast tree by selecting the path whose cost is the least; if the path’s delay destroys the delay upper bound, the least-cost path which meets the delay upper bound can be constructed through the least-cost path, and then is used to take the place of the least-cost path to join the current multicast tree. By the way, a low-cost multicast spanning tree can be constructed and the delay upper bound isn’t destroyed. Experimental results through simulations show that the new algorithm is superior to DCMPH_1 algorithm in the performance of spanning tree and the space complexity.
1. Introduction
Multicast consists of concurrently sending the same information from a source to a subset of all possible destinations in a computer network. With the development of highperformance network technology, such as video on demand, teleconferencing, online education and much more wide range of real-time multimedia applications, multicast technology is becoming crucial to support these technologies. The multicast routing algorithm is one of the key technologies to achieve multicast communication, with a good performance to build a multicast tree is often the best choice for multicast routing algorithms. A good multicast routing algorithm is often able to shorter time and meet certain quality of service (QoS) constraints on the minimum network bandwidth consumption, and thus use of network resources efficiently. Since delay is an important signal of QoS, while real-time multimedia applications have become increasingly demanding on the time delay, the study for multicast routing algorithm which meets end to end delay constraint and optimizes network resources is very important and is also a popular research topic [1].
Optimization of network resources from a global point of view can be seen as optimizing the overall costs of multicast routing tree. Finding the minimum cost multicast routing tree can be formalized as the Steiner tree problem in Graph Theory. As Solving the Steiner tree problem is NP-hard problem [2], therefore, many scholars put forward to calculating the quasi-Steiner heuristic tree, the most typical is the MPH algorithm [3], with the algorithm a computing member node can join the multicast tree by selecting the path whose cost is the least to the existing multicast tree. Literature [4] proposed the KPP algorithm that extends the KMB algorithm to support delay constraint. Firstly the algorithm finds the least cost path which meets the delay upper bound between any two nodes in the network; and then based on the path, the complete graph only contained the source node and destination nodes is constructed; finally uses of the heuristic algorithm based on minimum spanning tree to construct a multicast tree. Literature [5] proposed the BSMA algorithm, firstly the algorithm uses the Dijkstra algorithm to calculate the minimum delay path from the source to each destination node, and then constructs the multicast tree; Secondly uses the k-Shortest Path algorithm to obtain the low-cost path under the delay constraint; finally the low-cost path is used to take the place of the higher cost path of the multicast tree, thus reducing the total cost of the multicast tree. Both KPP and BSMA algorithm can produce high performance multicast tree, but the calculation is too large, so it is difficult to apply to the practice. Literature [6] proposed the CDKS algorithm, firstly the algorithm uses the Dijkstra algorithm to calculate the unconstrained destination optimal costs tree, if the path’s delay destroys the delay upper bound, then re-use the Dijkstra algorithm to calculate the minimum delay tree, and finally merges the two trees, at the same time removes the loops that may exist. The algorithm has much lower time than the previous two algorithms, but the spanning tree has excessive high cost. Literature [7] proposed the DCMPH algorithm, the algorithm based on the MPH algorithm's basic ideas to construct the multicast tree. Compared with other similar algorithms, it has a relatively lower time complexity and is high-performance in constructing the multicast tree, but the algorithm can not choose the next destination node to be added reasonably. Thus, Literature [8] proposed the DCMPH_1 algorithm. The algorithm is superior to DCMPH algorithm in the performance of spanning tree and space complexity through improvement on the search path, but the algorithm in choosing the next destination node to join the path is not optimal, so the cost performance of the spanning tree is not the most favorable. Thus DCMPH_1 algorithm is improved in this paper, a new multicast routing algorithm DCMPH_2 is presented.
2. Multicast Network Model and Related Definitions
In general, the network is formulated as an undirected graph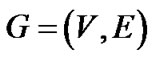 , where V is the set of nodes and E is the set of edges. The nodes in V represent the hosts or the routers in the network. The edges in E represent the communication links connecting the routers.
, where V is the set of nodes and E is the set of edges. The nodes in V represent the hosts or the routers in the network. The edges in E represent the communication links connecting the routers.  are the nodes of the graph,
are the nodes of the graph,  are the number of edges or the link numbers in G. Two positive real functions are defined on every edge
are the number of edges or the link numbers in G. Two positive real functions are defined on every edge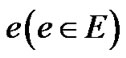 :
:
cost function : cost is determined by the utilization of the link. It denotes the cost to use the link.
: cost is determined by the utilization of the link. It denotes the cost to use the link.
delay function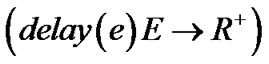 : delay is defined as the sum of the perceived queuing delay, transmission delay and propagation delay over the link.
: delay is defined as the sum of the perceived queuing delay, transmission delay and propagation delay over the link.
In a multicast communication session, there is a source node  and a member set
and a member set . s is the node corresponding to the source that generates the data. The nodes in M, called member nodes, correspond to the destinations that receive the data. The delay constraint Steiner tree T is rooted as node s and can reach all the destination nodes, and under the delay constraint, make the minimum network cost, Namely
. s is the node corresponding to the source that generates the data. The nodes in M, called member nodes, correspond to the destinations that receive the data. The delay constraint Steiner tree T is rooted as node s and can reach all the destination nodes, and under the delay constraint, make the minimum network cost, Namely , in the condition of
, in the condition of , make
, make  the minimum. whereΔis a positive real number, indicating from the source node to any node in the path that must be met end to end delay constraints, p(s,v) indicates that the path from s to v in the multicast tree.
the minimum. whereΔis a positive real number, indicating from the source node to any node in the path that must be met end to end delay constraints, p(s,v) indicates that the path from s to v in the multicast tree.
Definition one Path(u,v) indicates that the simple path from node  to node
to node , path delay is defined as the sum of the delay of each link, denoted Delay(Path(u,v)), namely:
, path delay is defined as the sum of the delay of each link, denoted Delay(Path(u,v)), namely:
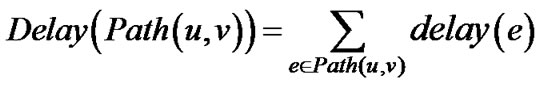
path cost is defined as the sum of the cost of each link, denoted Cost( Path(u,v) ), namely:

Definition two Steiner nodes: the nodes in the multicast tree other than source node and destination nodes.
Definition three path nodes: in the shortest path from node  to the spanning tree, the Steiner nodes between node u and the destination node are called the path nodes of the node.
to the spanning tree, the Steiner nodes between node u and the destination node are called the path nodes of the node.
Definition four parent edge: in the new spanning tree T, s is the source node,  , then there is one and only one path on the tree
, then there is one and only one path on the tree , then the edge
, then the edge  is the parent edge of
is the parent edge of .
.
3. DCMPH_2 Algorithm
3.1. DCMPH_1 Algorithm Analysis and Improvement
DCMPH_1 algorithm’s basic ideal is mainly based on the characteristics of generating low cost of MPH Steiner tree, combined with Dijkstra SPT algorithm is extended to the case of delay constrained minimum cost problem. The ideal of the algorithm is as follows:
Introduce two sets D and V, D denotes the minimum delay path set from source node s to each terminal node m. and V denotes the minimum cost path set from each end note m to the rest of the nodes that meet the delay constraint. Firstly, the algorithm uses the Dijkstra algorithm to calculate the minimum delay path from source node s to any end node m, at the same time initialize the set D, if there is an end node does not meet the delay constraint, then exit immediately, that is to say the delay-constrained multicast tree can not be found; then uses the improved Dijkstra algorithm to find the delay-constrained minimum cost path from end nodes to each node of the rest and initialize the set V; Then takes the source node s as the initial multicast tree T; finally chooses the end node u which meet the delay constraint and the minimum cost to the tree T and has not yet in the tree T, at the same time chooses the relative path p from the set V, if it can not find such u and p, then chooses the end node u which has the minimum cost and has not yet added to the tree T, at the same time chooses the relative path p, then u and p will be added to the spanning tree T. If there are loops, just simply delete the parent node that forms the loop edges. Repeat these steps until all the end nodes are added to the T. Two weaknesses in the algorithm can be seen from the above:
1) Firstly, the algorithm chooses the minimum cost path from the set V, if it can not find the path which meet the delay constraint, then selects the path from the minimum delay path set D. As the set D saved the minimum delay path from source node s to any end node m, so the algorithm adds additional space cost.
2) The minimum delay path selected may not be the optimal path, it may not be the best choice of the path’s cost, therefore, the performance of multicast tree generated by the algorithm is not very superior.
According to these problems, this paper proposed DCMPH_2 algorithm, the new algorithm is briefly described as follows:
Introduce a set V, V denotes the minimum cost path set from each end note m to the rest of the nodes that meet the delay constraint.
1) Uses the Dijkstra algorithm to calculate the minimum delay tree from source node s to any end node, then judges whether there is a low-cost delayconstrained multicast tree; if there is not exist, then exit immediately.
2) Uses the improved Dijkstra algorithm to find the delay-constrained minimum cost path from end nodes to each node of the rest and initializes the set V.
3) Takes the source node s as the initial multicast tree T.
4) Chooses the end node u which meets the delay constraint and the minimum cost to the tree T and has not yet in the tree T, at the same time chooses the relative path p from the set V, if it can not find such u and p, then finds node w in the minimum cost path from source node s to the end node u, if the total delay of the minimum delay path from s to w adds the delay of the minimum cost path from w to u meet the delay constraint, then adds the relative path to the tree T. If there are loops, just simply delete the parent node that forms the loop edges.
5) Repeat 4) until all the end nodes are added to the T.
Based on the above analysis, the algorithm is described as follows:
Input: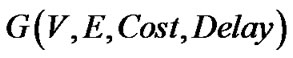 ,
,  ,
, 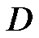 ,
, 
Output: Delay-constrained Steiner tree spanning
spanning 

1) 
2) If then return Null 3)
then return Null 3)  is the set of destination nodes*/
is the set of destination nodes*/
4) 
5) While ( is not Null) Do 6) Choose the end node
is not Null) Do 6) Choose the end node which meets the delay constraint and the minimum cost to the tree
which meets the delay constraint and the minimum cost to the tree  and has not yet in the tree
and has not yet in the tree 
7) 
8)  {The path from
{The path from  to the tree
to the tree 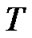 which is the minimum cost and meets the delay constraint}
which is the minimum cost and meets the delay constraint}
9) Else 10) 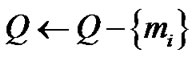
11)  {The minimum delay path from source node
{The minimum delay path from source node to node
to node adds the minimum cost path from node
adds the minimum cost path from node to the destination node
to the destination node  }
}
12) If there are loops, then delete 13) End If 14) End While 15) Return
DCMPH_2 algorithm do not save the minimum delay path from the source node to each end node, so compared with the DCMPH_1 algorithm, it has a relatively low space complexity. The fourth step of the algorithm if it can not find the minimum cost delay path from the set V, then selects the right path to construct delay-constrained path from the source node to end nodes, then adds the path to the original multicast tree. But the DCMPH_1 algorithm just selects the path from the minimum delay path set, although the path meets the delay constraint, the cost may not be optimal. Therefore, the algorithm chooses the right path through the tree to reduce the cost and improve the performance of the entire tree. In addition, the improved Dijkstra algorithm is introduced in detail in Literature [6].
3.2. DCMPH_2’s Time and Space Complexity Analysis
Theorem 1 The time complexity of DCMPH_2 algorithm is  ((m + 1) n2 + m2n)
((m + 1) n2 + m2n)
Proof: suppose that the number of the network is n, s is the source node, m is the number of the end node. In the first step the algorithm generates a minimum delay tree rooted as source node s, run the Dijkstra algorithm once, its time complexity in the worst case is 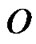 (n2). In the second step uses the improved Dijkstra algorithm to find the delay-constrained minimum cost path from end nodes to each node of the rest, then the time complexity is
(n2). In the second step uses the improved Dijkstra algorithm to find the delay-constrained minimum cost path from end nodes to each node of the rest, then the time complexity is  (mn2). The time complexity of the third step is constant time
(mn2). The time complexity of the third step is constant time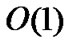 . The fourth step selects the delay-constrained end node to the tree, considering the number of comparisons: suppose there are i th end nodes have been added to the multicast tree, then decide the (i + 1) th to join the tree, in the worst case, the spanning tree T has (n – m + i) th nodes, there are (m – i) th end nodes have not been added to the tree, if it can not be found in the set V, in the worst case it need compare n(m – i) times for the nodes whose path’s delay destroys the delay upper bound, so it need compare
. The fourth step selects the delay-constrained end node to the tree, considering the number of comparisons: suppose there are i th end nodes have been added to the multicast tree, then decide the (i + 1) th to join the tree, in the worst case, the spanning tree T has (n – m + i) th nodes, there are (m – i) th end nodes have not been added to the tree, if it can not be found in the set V, in the worst case it need compare n(m – i) times for the nodes whose path’s delay destroys the delay upper bound, so it need compare 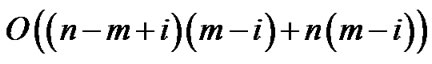 times to find the best path, so the cycle complexity of the fourth and fifth step is:
times to find the best path, so the cycle complexity of the fourth and fifth step is:

Therefore the total time complexity is  ((m + 1) n2 + m2n). The time complexity of BSMA algorithm is
((m + 1) n2 + m2n). The time complexity of BSMA algorithm is  (kn3), The time complexity of KPP algorithm is
(kn3), The time complexity of KPP algorithm is  (Δn3), whereΔis the integer value for the maximum delay. So the time complexity of DCMPH _2 algorithm is far lower than BSMA and KPP algorithms, but slightly higher than the CDKS algorithm, the time complexity of CDKS algorithm is
(Δn3), whereΔis the integer value for the maximum delay. So the time complexity of DCMPH _2 algorithm is far lower than BSMA and KPP algorithms, but slightly higher than the CDKS algorithm, the time complexity of CDKS algorithm is (n2). The time complexity of DCMPH_1 algorithm [8] is
(n2). The time complexity of DCMPH_1 algorithm [8] is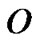 ((m + 1) n2 + m2n ), so the time complexity of DCMPH_2 algorithm is considerable with the DCMPH_1 algorithm.
((m + 1) n2 + m2n ), so the time complexity of DCMPH_2 algorithm is considerable with the DCMPH_1 algorithm.
From the analysis of DCMPH_1 and DCMPH_2 algorithm, we can find that the space cost of the algorithm mainly concentrated on the second and the fourth steps, which DCMPH_1 algorithm stores m *δ + m paths, where δ is the maximum number of paths that meet delay constraint from an arbitrary end node m to the remaining nodes. The DCMPH_2 algorithm only stores m *δ + β paths, where δ is the maximum number of paths that meet delay constraint from an arbitrary end node m to the remaining nodes, β is the number of the delay-constraint path constructed through the remaining nodes in the minimum cost path. So β ≤ m. Therefore, in the worst circumstances, DCMPH_2 algorithm’s space complexity is the same as DCMPH_1 algorithm.
4. Simulation and Analysis
In order to verify the correctness and validity of DCMPH_ 2 algorithm, the simulation model used in this paper is proposed in Literature [9,10], in the network model: nth nodes are randomly distributed in the Cartesian coordinate system (assuming the node coordinates are integer), the cost of each edge is the random value of (0,5). Delay is consistent with the delay of the literature. The connectivity between nodes is determined by:

 is the distance between u and v; L is the max distance between two arbitrary nodes; δ and β are the parameters to regulate the network map feature. In order to make the random network model near to the realistic, this paper selects δ = 0.3, β = 0.3. The data used in the simulation experiment are the average result of 50 times, different source nodes and receive nodes are in the same conditions.
is the distance between u and v; L is the max distance between two arbitrary nodes; δ and β are the parameters to regulate the network map feature. In order to make the random network model near to the realistic, this paper selects δ = 0.3, β = 0.3. The data used in the simulation experiment are the average result of 50 times, different source nodes and receive nodes are in the same conditions.
Figure 1 shows the relationship between the cost of the multicast tree and the network nodes, select the same 20th receive nodes, the network node increase from 60 to 120, and each time the number of nodes in the network increased by 10, delay constraint remains 0.03 s. From the figure we can see the multicast tree cost generated by DCMPH_2 is less than DCMPH_1 algorithm.
Figure 2 shows the relationship between the multicast tree cost and the number of group members, delay constraint remains 0.03 s, the number of nodes in the network maintain the same 120, but the nodes in the multicast group number from 20 to 80, from the figure can be seen, DCMPH_2 algorithm is better than DCMPH_1 algorithm, but with the increase in the number of the receive nodes, this advantage disappeared gradually.
Figure 3 shows the relationship between the multicast tree cost and the delay constraint. Experiments are in the network environment without any changes, delay restriction increased from 4 to 24, MPH algorithm produced
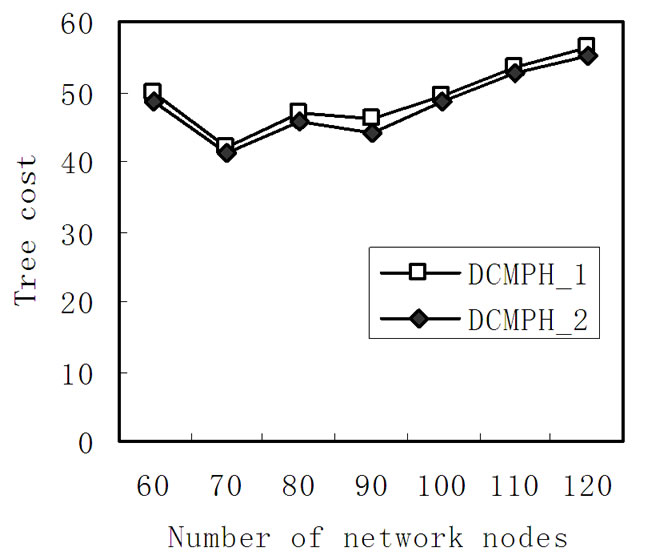
Figure 1. Relation between the cost and size of network nodes.
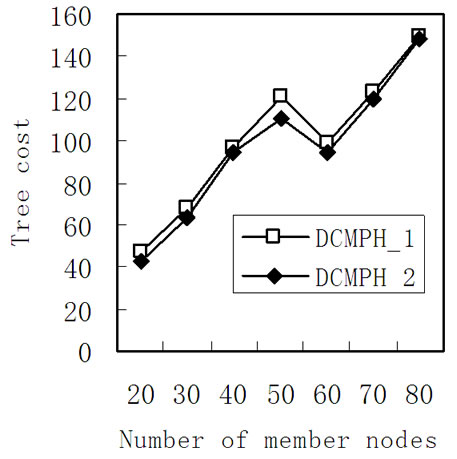
Figure 2. Relation between the cost and size of member nodes.

Figure 3. Relation between the cost and delay threshold.
the multicast tree under the conditions of without delay constraint, so it has the minimum cost, and this experiment take the MPH algorithm as the benchmark. Through the Figure 3 we can see the DCMPH_2 algorithm is better than the DCMPH_1 algorithm, and with the delay constraint increases, DCMPH_2 close to the MPH algorithm faster than the DCMPH_1 algorithm.
Figure 4 shows the relationship between the space complexity of the algorithm and the network nodes, this experiment statistics the number of minimum cost path to measure the space complexity. We can see in Figure 4 as the number of nodes increases, the space complexity of the algorithm DCMPH_2 is lower than the algorithm DCMPH_1, with the number of nodes increases, this trend is more obvious.
5. Conclusions
MPH algorithm is a superior performance of Steiner tree heuristic, the paper analysis and improves the DCMPH_ 1 algorithm under the delay-constrained multicast routing environment, proposed the DCMPH_2 algorithm. The algorithm has better effect than the DCMPH_1 algo rithm, and it can quickly construct the delay-constrained multicast tree, so meets the needs of real-time multicast
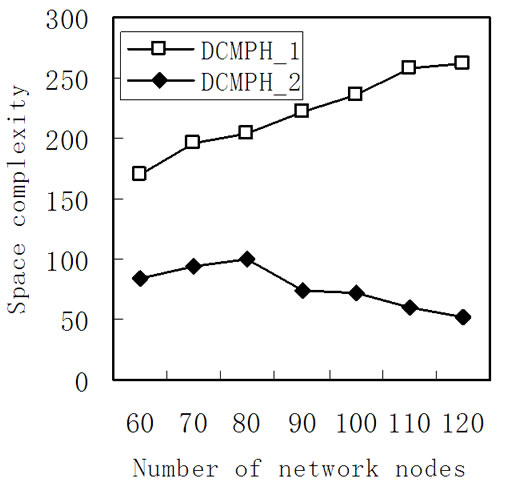
Figure 4. Relation between the space complexity and size of network nodes.
multimedia applications effectively.
6. Acknowledgements
This work is supported by the Chongqing Municipal Education Commission of Science and Technology Research Project of China under grant 2009 KJ090509.
7. References
[1] L. L. Gao and W. S. Li, “A New Delay Constraint Multicast Routing Algorithm,” Computer Technology and Development, Vol. 16, No. 10, 2006.
[2] D. T. Lotarev and A. P. Uzdemir, “Conversion of the Steiner Problem on the Euclidean Plane to the Steiner Problem on Graph,” Automation and Remote Control, Vol. 66, No. 10, 2005, pp. 1603-1613. doi:10.1007/s10513-005-0194-y
[3] P. WINTER, “Steiner Problem in Networks: A Survey,” Networks, Vol. 17, No. 2, 1987, pp. 129-167. doi:10.1002/net.3230170203
[4] V. Kompella, J. C. Pasquale and G. C. Polyzos, “Multicast Routing for Multimedia Communication,” IEEE/ACM Transaction on Networking, Vol. 1, No. 3, 1993, pp. 286-292. doi:10.1109/90.720901
[5] M. Parsa, Q. Zhuo and I. J. Garcia-Luna-Aceves, “An Iterative Algorithm for Delay-Constrained Minimum Cost Multicasting,” IEEE/ACM Transaction on Networking, Vol. 6, No. 4, 1998, pp. 461-474. doi:10.3724/SP.J.1087.2010.03056
[6] Q. Sun and H. Langendorfer, “Efficient Multicast Routing for Delay-Sensitive Applications[EB/OL],” 2009. http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=AC50DDEAFE5841993DFA381CFCA0C624?
[7] L. Zhou and Y. M. Sun, “A Delay-Constrained Steiner Tree Algorithm Using MPH,” Journal of Computer Research and Development, Vol. 45, No. 5, 2008, pp. 810-816.
[8] C. D. Yang, K. Huan and Y. N. Ding, “A New MPH-Based Delay-Constrained Steiner Tree Algorithm,” Journal of Computer Applications, Vol. 30, No. 11, 2010, pp. 3056- 3058. doi:10.1109/49.12889
[9] B. M. Waxman, “Routing of Multicast Connections,” IEEE Journal on Selected Areas in Communications, Vol. 6, No. 9, 1988, pp. 1617-1622. doi:10.1109/49.12889
[10] Y. P. Yu, “Studies on Multicast Routing Algorithms,” Doctoral Dissertation, Zhejiang University, Hangzhou, 2002.

