Received 31 August 2015; accepted 10 October 2015; published 13 October 2015

ABSTRACT

The classical example of no-where differentiable but everywhere continuous function is Weierstrass function. In this paper we have defined fractional order Weierstrass function in terms of Jumarie fractional trigonometric functions. The Hölder exponent and Box dimension of this new function have been evaluated here. It has been established that the values of Hölder exponent and Box dimension of this fractional order Weierstrass function are the same as in the original Weierstrass function. This new development in generalizing the classical Weierstrass function by use of fractional trigonometric function analysis and fractional derivative of fractional Weierstrass function by Jumarie fractional derivative, establishes that roughness indices are invariant to this generalization.

Keywords:

Hölder Exponent, Fractional Weierstrass Function, Box Dimension, Jumarie Fractional Derivative, Jumarie Fractional Trigonometric Function

1. Introduction

The concepts of fractional geometry, fractional dimensions are important branches of science to study the irregularity of a function, graph or signals [1] - [3] . On the other hand fractional calculus is another developing mathematical tool to study the continuous but non-differentiable functions (signals) where the conventional calculus fails [4] - [11] . Many authors are trying to relate the fractional derivative and fractional dimension [1] [12] - [15] . The functions which are continuous but non-differentiable in integer order calculus can be characterized in terms of fractional calculus and especially through Holder exponent [10] [16] . To study the no-where differentiable functions authors in [12] - [16] used different types of fractional derivatives. Jumarie [17] defined the fractional trigonometric functions in terms of Mittag-Leffler function and established different useful fractional trigonometric formulas. The fractional order derivatives of those functions were established in-terms of the Jumarie [17] [18] modified fractional order derivatives. In this paper we have defined the fractional order Weierstrass functions in terms of the fractional order sine function. The Hölder exponent and box-dimension (fractional dimension) of graph of this function have been obtained here. The fractional order derivative of this function has also established here. This is a new development in generalizing the classical Weierstrass function by usage of fractional trigonometric functions including the study of its character. The paper is organized as: Section 2 deals with description of Jumarie fractional derivative, Mittag-Leffler function of one and two parameter types; fractional trigonometric function of one and two parameter types and derivation of Jumarie fractional derivatives of those functions. In this section we also have derived some useful relations of fractional trigonometric functions which shall be used for our further calculations―in characterizing fractional Weierstrass function. We have continued this section by introducing Lipschitz Hölder exponent (LHE)―its definition, its relation to Hurst exponent and fractional dimension and also definition of Hölder continuity. The classical Weierstrass function has also been defined here. These Lipschitz Hölder exponent, Hurst exponent, and fractional dimension are basic parameters to indicate roughness index of a function or a graph. In Section 3 we have described the fractional Weierstrass function by generalizing the classical Weierstrass function by use of fractional sine trigonometric function. Subsequently we apply derived identities of fractional trigonometric functions to evaluate the properties of this new fractional Weierstrass function. In Section 4 we have done derivation of properties of fractional derivatives of fractional Weierstrass function, and concluded the paper with conclusion and references.

2. Jumarie Fractional Order Derivative and Mittag-Leffler Function

a) Fractional Order Derivative of Jumarie Type

Jumarie [17] defined the fractional order derivative by modifying the Left Riemann-Liouvellie (RL) fractional derivative in the following form for the function 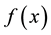in the interval a to x, with 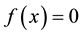for.

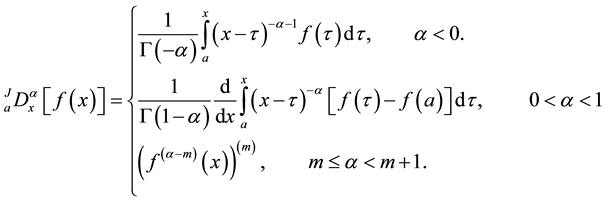(1)

In the above definition, the first expression is just the Riemann-Liouvelli fractional integration; the second line is Riemann-Liouvelli fractional derivative of order 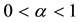of offset function that is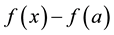. For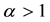, we use the third line; that is first we differentiate the offset function with order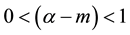, by the formula of second line, and then apply whole m order differentiation to it. Here we chose integer m, just less than the real number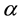; that is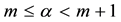. In this paper we use symbol 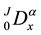to denote Jumarie fractional derivative operator, as defined above. In case the start point value is un-defined, there we take finite part of the offset function as; for calculations. Note in the above Jumarie definition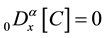, where C is constant function, otherwise in RL sense, the fractional derivative of a constant function is

, that is a decaying power-law function. Also we purposely state that 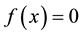for

in order to have initialization function in case of fractional differ-integration to be zero, else results are difficult [9] .

b) Mittag-Leffler Function and Its Jumarie Type Fractional Derivative: One and Two Parameter Type

1) One Parameter Mittag-Leffler Function

The Mittag-Leffler function [19] - [22] of one parameter is denoted by and defined by

(2)

This function plays a crucial role in classical calculus for, for it becomes the exponential function, that is

(3)

We now consider the Mittag-Leffler function in the following form in infinite series representation for for and for as;

(4)

Then taking Jumarie fractional derivative of order term by term for the above series we obtain the following by using the formula and

(5)

Like the exponential function; play important role in fractional calculus. The function is a fundamental solution of the Jumarie type fractional differential equation, where is Jumarie derivative operator as described above.

Jumarie in [18] established. We reproduce the Proof of the above relation. Let us consider a function which satisfies the condition

Differentiating both side with respect to x and y of -order respectively we get the following.

First consider y a constant, and we fractionally differentiate w.r.t. x by Jumarie derivative

Now we consider x as constant and do the following steps

Here we put equivalence of, with C as constant; that is when x or y are taken as constant the function form of these two quantities gets equivalent that is equivalent to as

Jumarie fractional derivative of constant is zero. Therefore the RHS of above two expressions are equal, from that we get the following

The above two may be equated to a constant say. Then we have, or we write. From the property of Mittag-Leffler function and Jumarie derivative of the Mittag- Leffler function we know that; we imply that the solution of is. Therefore satisfies the condition , or. Considering, we therefore can write the following identity

Using definition we expand the above as depicted below

Comparing real and imaginary part in above derived relation we get the following

This is very useful relation as in conjugation with classical trigonometric functions, and we will be using these relations in our analysis of fractional Weierstrass function and its fractional derivative.

2) Two Parameter Mittag-Leffler Function

The other important function is the two parameter Mittag-Leffler function denoted by and defined by,

(6)

The functions (2) and (6) play important role in fractional calculus, also we note that. Again from Jumarie definition of fractional derivative we have and.

Again we derive Jumarie derivative of order for one parameter Mittag-Leffler function and thereby get two parameter Mittag-Leffler function. For finding term by term Jumarie derivative we use and.

(7)

where is two parameter Mittag-Leffler function.

c) Jumarie Definition of Fractional Sine and Cosine Function and Their Fractional Derivative: Both One Parameter and Two Parameter Type

1) One Parameter Sine and Cosine Function

Jumarie [18] defined the one parameter fractional sine and cosine function in the following form,

(8a)

(8b)

(8c)

From Figure 1 and Figure 2 it is observed that for both the fractional trigonometric functions and is decaying functions like damped oscillatory motion. For it is like simple harmonic motion with sustained oscillations; and for it grows while it oscillates infinitely; like unstable oscillator.

The series representation of for and for is following

Taking term by term Jumarie derivative we get,

(9)

The series presentation of, for with for is

Taking term by term Jumarie derivative we get

(10)

Thus we get

and

2) Two Parameter Sine and Cosine Function

Let us define the two parameter sine and cosine functions and as depicted below:

Now with this and with definition of two parameter Mittag-Leffler function (3) with imaginary argument we get the following useful identity

Now for, we do the Jumarie derivative of order on the function as depicted in following steps, with formula and.

Thus we get a very useful relation

Similarly it can be shown that

Now we calculate the Jumarie type fractional order derivative of like we did for by using the formula and.

On the other hand the Jumarie type fractional order derivative of is following, as we did for by using the formula and.

We obtain

Similarly the Jumarie type fractional order derivative of is

2.1. Definition of Some Useful Roughness Indices

a) Lipschitz Hölder Exponent (LHE)

A function is said to have LHE [1] it satisfies the following condition

where is a small positive number. The property LHE defined above corresponds to local property. The global LHE in interval is denoted by and is defined by

unless is a constant function,. The Lipschitz Holder exponent is sometimes named as Holder exponent. For the continuous function, satisfies the Lipschitz condition on its domain of definition if when, where is small positive number, and is real constant. This function has Holder exponent as unity.

Consider the function:

such that then when is a function with Holder exponent 1. In a way it states that the continuous function in consideration is one-whole differentiable and the value of differentiation is bounded, that is for.

b) Holder Continuity

A continuous function which is non-differentiable in classical sense is said to holder continuous with exponent if

where is a real constant and.

c) Fractional Dimension

Fractional dimension (d) or box dimension [1] of a function or graph is local property, denotes the degree of roughness of a function or graph. Let the graph of a function is for can be covered by N-squares of size r then with the fractional dimension of the graph is defined as,

Again if H be the Hurst exponent then the relation between the above Holder exponents are [1] [9] . The Holder and Hurst exponents are equivalent for uni-fractal graphs that has a constant fractional dimension in defined interval [1] [9] .

3. The Fractional Weierstrass Function

In 1872 K. Weierstrass [23] - [25] proposed his famous example of an everywhere continuous but no-where differentiable function on the real line with two parameters in the following form

where b is odd-integer. He proved that this function is continuous for all and is non-differentiable for all real values of x provided. Considering b a constant say a constant and assuming, and another presentation of the Weierstrass function [13] can be obtained which is

(11)

In reference [13] Falconer established the fractional dimension of Weierstrass function defined in (11) is s and the corresponding Holder exponent is.

We define the fractional Weierstrass Function in terms of Jumarie [2008] fractional sine function, that is in the following form for

(12)

where, , and for it reduces the original Weierstrass Function, and a condition that for.

We only are stating some lemmas which will be used to characterize the fractional Weierstrass function and its fractional derivative.

Lemma 1:

Let f be function continuous in interval and [12] -[14] .

Suppose

1)

then the dimension [12] - [14] of the graph f is.

2) Suppose. For every, and there exists such that and then the dimension [12] -[14] of the graph f is.

Theorem 1: The Holder exponent of fractional Weierstrass function with is and consequently the Hausdorff dimension or fractional dimension is s over any finite interval suppose it is.

Proof: We calculate in following steps where we have used our derived expression

From the series expansion of and and also from the Figure 1 and Figure 2, it is clear that for small x, and also both and is less than or equal to 1. Therefore, with above observation that is for small h, , and for large h, we write the following

Choose then one can find positive integer m such that then divide the summa-

tion that is into two parts. First part for to m then and for other values of k maximum value of the expression in third bracket is equal to 1. We use the geometric series formulas and,for in the following derivation.

With, that is we get the following

where the constant. From definition of Holderian function and the above discus-

sion it is clear that fractional Weierstrass function is also Holder continuous with Holder exponent, a fractional number. This shows (by Lemma-1) that Hausdorff dimension of graph of fractional Weierstrass function is. Thus the Hausdorff dimension of fractional Weierstrass function and original Weierstrass function is same, is independent of fractional exponent () as defined in (11).

4. The Jumarie Fractional Derivative of Fractional Weierstrass Function

Many authors found the fractional derivative of the continuous but nowhere differentiable function that is Weierstrass Function [10] -[17] using different type definitions of fractional derivatives. Here we consider Jumarie type fractional order derivative of is of order

We used in above derivation the identity. Therefore from above derivation we obtain the following,

(5)

Since if then is a bounded function and therefore will be bounded function if is convergent. Since is a geometric series will be conver-

gent if implying. Hence the fractional derivative of order with of the Weierstrass Function will exists when.

Again if then and for are unbounded functions (Figure 1 and Figure 2) and will grow by oscillating without bound to for. Since and implying therefore is a divergent series. Therefore

is a divergent series for. We write following observation

This shows that -order Jumarie fractional derivative of the fractional Weierstrass function exists when and for it does not exist. Thus we can state a theorem in the following form

Theorem 2: -order Jumarie fractional derivative of the fractional Weierstrass function

exists when and for it does not exist.

Theorem 3: The Holder exponent of -order fractional derivative of fractional Weierstrass function, is and consequently the Hausdorff dimension or fractional dimension is over any finite interval.

Proof: Let

denotes -order fractional Jumarie derivative of fractional Weierstrass function. Then using the identity we get the following

From the series expansion of and and also from the Figure 1 and Figure 2 it is clear that for small x, and also both and is less than or equal to 1. Therefore, with above observation that is for small h, , and for large h, we write the following

Choose then one can find positive integer m such that then as per our earlier derivation for we do the following steps

With, that is we get the following

where. From definition of Holderian function and above discussion it is clear that -order fractional derivative of fractional Weierstrass function is also Holder continuous

with Holder exponent. This shows that Hausdorff dimension of graph of fractional Weierstrass function is (by lemma-1). The graph dimension increased by fractional order for fractional derivative of Weierstrass function by amount of fractional derivative-the graph becomes rougher.

5. Conclusion

The fractional Weierstrass function is a continuous function for all real values of the arguments, and its box dimension and Holder exponent are independent of fractional order that incorporates to the fractional Weierstrass functions. Again the Box dimension of fractional derivative of the fractional Weierstrass increases with increase of order of fractional derivative. This invariant nature of the roughness index of fractional Weierstrass function when generalized with fractional trigonometric function is remarkable. The other embodiment in similar lines as in this paper to get different fractional Weierstrass function is under development.

Acknowledgements

Acknowledgments are to Board of Research in Nuclear Science (BRNS), Department of Atomic Energy Government of India for financial assistance received through BRNS research project no. 37(3)/14/46/2014-BRNS with BSC BRNS, title “Characterization of unreachable (Holderian) functions via Local Fractional Derivative and Deviation Function”. Authors are also thankful to the reviewer for his valuable comments which has helped to improve the paper.

Cite this paper

UttamGhosh,SusmitaSarkar,ShantanuDas, (2015) Fractional Weierstrass Function by Application of Jumarie Fractional Trigonometric Functions and Its Analysis. Advances in Pure Mathematics,05,717-732. doi: 10.4236/apm.2015.512065

References